自监督去噪:Recorrupted-to-Recorrupted原理分析与总结

文章目录
- 1. 方法原理
- 1.1 相关研究
- 1.2 研究思路
- 1.3 小结
- 2. 实验结果
- 3. 总结
文章地址: https://ieeexplore.ieee.org/document/9577798/footnotes#footnotes
参考博客: https://github.com/PangTongyao/Recorrupted-to-Recorrupted-Unsupervised-Deep-Learning-for-Image-Denoising
1. 方法原理
1.1 相关研究
Noise2Noise的问题
- 噪声图像对不好获取
- 同一场景不同图像怎么对齐?
解决N2N配对问题的工作可以分为两类
-
数据增强方法:
- Noise2Void 和 Noise2Self使用盲点网络的方法避免过拟合(直接点到点映射)
- Noiser2Noise 和 Noise-as-Clean 是采样额外的噪声数据配对进行训练
-
正则化去噪的DNN:
- Stein’s Unbiased Risk Estimator(SURE)通过添加对预测结果散度的惩罚添加正则
- Deep Image Prior 使用 early-stopping 防止过拟合
- Self2Self中使用 Dropout引入不确定性估计,提高去噪的鲁棒性。
研究动机
- 无监督/自监督学习在实际工作、缺少干净数据的时候是非常有效的
- 现有的无监督方法还无法和监督学习媲美
1.2 研究思路
从可加性的高斯噪声出发,配对的噪声数据对科比表示为
y = x + n n ∼ N ( 0 , σ 1 2 I ) y ′ = x + n ′ n ′ ∼ N ( 0 , σ 2 2 I ) \begin{aligned} y &= x + n ~~~~ n \sim N(0,\sigma_1^2 I) \\ y' &= x + n' ~~~~ n' \sim N(0,\sigma_2^2 I) \end{aligned} yy′=x+n n∼N(0,σ12I)=x+n′ n′∼N(0,σ22I)
Noise2Noise的L2损失函数需要优化
E n , n ′ { ∣ ∣ F θ ( y ) − y ′ ∣ ∣ 2 2 } E_{n,n'}\{ ||F_{\theta}(y) - y'||_2^2\} En,n′{∣∣Fθ(y)−y′∣∣22}
将其展开进行推导
E n , n ′ { ∣ ∣ F θ ( y ) − y ′ ∣ ∣ 2 2 } = E n , n ′ { ∣ ∣ F θ ( y ) − x − n ′ ∣ ∣ 2 2 } = E n , n ′ { ∣ ∣ F θ ( y ) − x ∣ ∣ 2 2 − 2 ( n ′ ) T ( F θ ( y ) − x ) + ( n ′ ) T n ′ } = E n , n ′ { ∣ ∣ F θ ( y ) − x ∣ ∣ 2 2 } − 2 E n , n ′ { ( n ′ ) T F θ ( y ) } + c o n s t \begin{aligned} &E_{n,n'}\{ ||F_{\theta}(y) - y'||_2^2\} \\ &= E_{n,n'}\{ ||F_{\theta}(y) - x - n'||_2^2\} \\ &= E_{n,n'}\{ ||F_{\theta}(y) - x||_2^2 - 2(n')^T(F_{\theta}(y) -x) + (n')^Tn' \} \\ &= E_{n,n'}\{ ||F_{\theta}(y) - x||_2^2\} - 2E_{n,n'}\{ (n')^T F_{\theta}(y)\} + const \end{aligned} En,n′{∣∣Fθ(y)−y′∣∣22}=En,n′{∣∣Fθ(y)−x−n′∣∣22}=En,n′{∣∣Fθ(y)−x∣∣22−2(n′)T(Fθ(y)−x)+(n′)Tn′}=En,n′{∣∣Fθ(y)−x∣∣22}−2En,n′{(n′)TFθ(y)}+const
如果噪声 n n n 和 n ′ n' n′ 是独立的,那么 E n , n ′ { ( n ′ ) T F θ ( y ) } = 0 E_{n,n'} \{(n')^T F_{\theta}(y)\} = 0 En,n′{(n′)TFθ(y)}=0,也就是说噪声对监督学习和噪声-干净数据的监督学习可以得到相同的优化结果。现在的问题就是如何从一张噪声图片( y y y)中构建出一对具有独立噪声的数据( y ^ , y ~ \widehat{y},\widetilde{y} y ,y )
根据假设,噪声的分布是 AWGN(additive white Gaussian noise),那么噪声服从分布 n ∼ N ( 0 , σ 1 2 I ) n \sim N(0,\sigma_1^2 I) n∼N(0,σ12I)。 现在根据下方的方法进行采样
y ^ = y + D T z , y ~ = y − D − 1 z , z ∼ N ( 0 , σ 1 2 I ) \widehat{y} = y + D^Tz,~~~ \widetilde{y} = y - D^{-1}z,~~~ z \sim N(0,\sigma_1^2 I) y =y+DTz, y =y−D−1z, z∼N(0,σ12I)
其中D可以是任何可逆矩阵,文章中证明了 噪声样本 y ^ \widehat{y} y 和 y ~ \widetilde{y} y 相互独立,所以根据这两个样本训练的网络满足
E n , z { ∣ ∣ F θ ( y ^ ) − y ~ ∣ ∣ 2 2 } = E n ^ { ∣ ∣ F θ ( x + n ^ ) − x ∣ ∣ 2 2 } E_{n,z}\{||F_{\theta}(\widehat{y}) - \widetilde{y}||_2^2\} = E_{\widehat{n}} \{ ||F_{\theta}(x + \widehat{n}) - x||_2^2 \} En,z{∣∣Fθ(y )−y ∣∣22}=En {∣∣Fθ(x+n )−x∣∣22}
其中 n ^ = n + D T z \widehat{n} = n + D^Tz n =n+DTz
那么对于这种无结构噪声数据:
y k = x k + n k , x k ∼ X , n k ∼ N ( 0 , σ 2 I ) y^k = x^k + n^k,~~~ x^k \sim X , ~~~ n^k \sim ~ N(0,\sigma^2I) yk=xk+nk, xk∼X, nk∼ N(0,σ2I)
用噪声数据对 { ( y ^ k , y ~ k ) (\widehat{y}^k, \widetilde{y}^k) (y k,y k)}定义的损失函数为也就等价于下面这个损失函数了
E x , n ^ { ∣ ∣ F θ ( x + n ^ ) − x ∣ ∣ 2 2 } E_{x,\widehat{n}}\{ ||F_{\theta}(x + \widehat{n}) - x||_2^2\} Ex,n {∣∣Fθ(x+n )−x∣∣22}
对于结构化的噪声数据,可以调整噪声数据的表示形式:比如噪声的分布和干净数据相关
n服从 N ( 0 , ∑ x ) N(0,\sum_x) N(0,∑x)的正态分布,可以将噪声对表示为
y ^ = y + ∑ x D T z , y ~ = y − ∑ x D − 1 z , z ∼ N ( 0 , I ) \widehat{y} = y + \sqrt{\sum_x}D^Tz , ~~~ \widetilde{y} = y - \sqrt{\sum_x}D^{-1}z, z \sim N(0,I) y =y+x∑DTz, y =y−x∑D−1z,z∼N(0,I)
其中协方差差矩阵 ∑ x \sum_x ∑x是正定矩阵,其满足 ∑ x T = ∑ x , ∑ x ∑ x = ∑ x \sqrt{\sum_x}^T = \sqrt{\sum_x}, ~~~ \sqrt{\sum_x}\sqrt{\sum_x} = \sum_x ∑xT=∑x, ∑x∑x=∑x
1.3 小结
- 从数学推导上证明了 R2R的方法和监督学习的可比性
- 相比其他无监督去噪方法,该方法简单且灵活,也可以直接在噪声图像上进行处理
- 去噪效果很好,在真实数据中也应用非常好
2. 实验结果
-
去除高斯噪声效果对比,R2R的效果比当前最好的 SURE 效果还要好。这里的 D = α I D = \alpha I D=αI 和 D − 1 = I / α D^{-1} = I/\alpha D−1=I/α,其中 α = 0.5 \alpha = 0.5 α=0.5
-
去除真实图片中的噪声:噪声水平函数(noisy level function)给定,噪声函数建模为 heteroscedastic signle dependent Gaussian single, 其协方差为
∑ x = d i a g ( β 1 x + β 2 ) \sum_x = diag(\beta_1 x + \beta_2) x∑=diag(β1x+β2)
设置 D = 2 I , D − 1 = I / 2 D = 2I , D^{-1} = I/2 D=2I,D−1=I/2。训练的结果展示R2R的效果在各种传统方法和无监督中是最好的,但是和监督学习仍然存在一定的差距。分析原因是:噪声模式和噪声水平函数的估计不准确 -
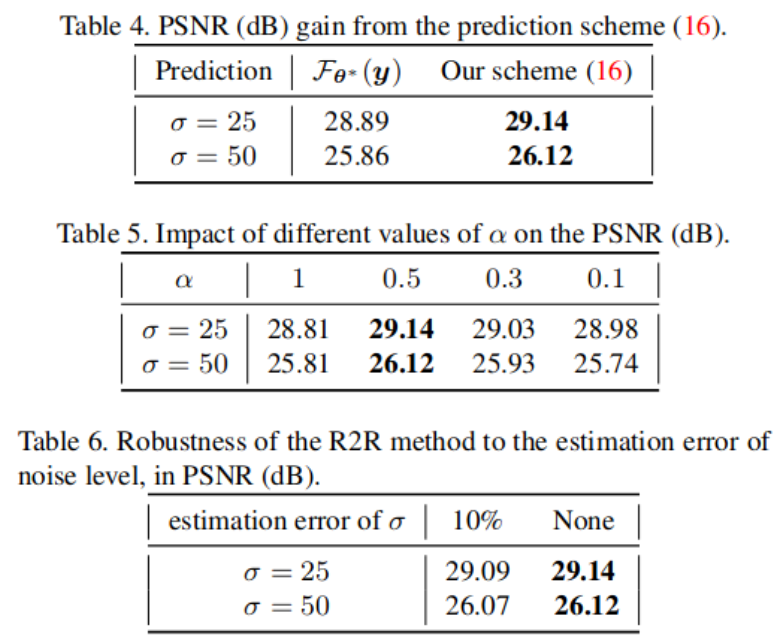
消融实验:比如对比不同的噪声水平的预测结果
3. 总结
优势:
- 相比Noise2Noise:不需要配对噪声图片,而是根据一张噪声图片加噪
- 相比Noiser2Noise:都是采样加噪,都需要估计噪声模式,但是本文的方法从数学上的推导更加严谨一些,同时也给定了如何加噪声的方式。
- 相比Noise2Void,Noise2Self:作者对比了效果,会更好(我自己还需要补一个实验证明)
- 这种方法可以应用到实际噪声之中,但是如何估计噪声模式是个大问题
- 可以处理结构噪声和无结构噪声
缺点:
- 需要估计噪声模式,网络会继承噪声模式估计的误差
- 对于不同的噪声模式,其构建噪声对的方法会有所不同;
- 对于不同的损失函数,这种方法是否也是需要修改?比如现在想要去除图片中的文字,那么使用L1损失函数明显是会比L2损失函数更有优势的。那么上面的推导是不是也需要相应地修改?
相关文章:
自监督去噪:Recorrupted-to-Recorrupted原理分析与总结
文章目录 1. 方法原理1.1 相关研究1.2 研究思路1.3 小结 2. 实验结果3. 总结 文章地址: https://ieeexplore.ieee.org/document/9577798/footnotes#footnotes 参考博客: https://github.com/PangTongyao/Recorrupted-to-Recorrupted-Unsupervised-Deep-Learning-for-Image-Den…...

【css】css实现水平和垂直居中
通过 justify-content 和 align-items设置水平和垂直居中, justify-content 设置水平方向,align-items设置垂直方向。 代码: <style> .center {display: flex;justify-content: center;align-items: center;height: 200px;border: 3px…...
常见Charles在Windows10抓包乱码问题
废话不多说 直接开整 最近反复安装证书还是乱码 网上各种百度还是不行 首先计算机查看安装好的证书 certmgr.msc 找到并删除掉 重新安装证书 具体解决方法: 第一步:点击 【工具栏–>Proxy–>SSL Proxying Settings…】 第二步:配置…...

汽车维修保养记录查询API:实现车辆健康状况一手掌握
在当今的数字化世界中,汽车维修保养记录的查询和管理变得前所未有地简单和便捷。通过API,我们可以轻松地获取车辆的维修和保养记录,从而实现对手中车辆健康状况的实时掌握。 API(应用程序接口)是进行数据交换和通信的标…...
)
正则表达式学习记录(Python)
正则表达式学习记录(Python) 一、特殊符号和字符 多个正则表达式匹配 ( | ) 用来分隔不同的匹配模式,相当于逻辑或,可以符合其中任何一个正则表达式 at | home # 表示匹配at或者home bat | bet | bit # 表示匹配bat或…...

Ubuntu20.04操作系统安装Docker
1、添加Docker仓库 curl -fsSL https://mirrors.ustc.edu.cn/docker-ce/linux/ubuntu/gpg | sudo apt-key add -sudo add-apt-repository \"deb [archamd64] https://mirrors.ustc.edu.cn/docker-ce/linux/ubuntu/ \$(lsb_release -cs) \stable"2、安装Docker sudo…...
python制作小程序制作流程,用python编写一个小程序
这篇文章主要介绍了python制作小程序代码宠物运输,具有一定借鉴价值,需要的朋友可以参考下。希望大家阅读完这篇文章后大有收获,下面让小编带着大家一起了解一下。 1 importtkinter2 importtkinter.messagebox3 importmath4 classJSQ:5 6 7 d…...

Github 创建自己的博客网站
参考pku大佬视频制作,附上B站视频:【GitHub Pages 个人网站构建与发布】 同时还参考了:【Python版宝藏级静态站点生成器Material for MkDocs】 GitHub Pages 介绍 内容参考:GitHub Pages - 杨希杰的个人网站 (yang-xijie.githu…...
Windows上安装 jdk 环境并配置环境变量 (超详细教程)
👨🎓博主简介 🏅云计算领域优质创作者 🏅华为云开发者社区专家博主 🏅阿里云开发者社区专家博主 💊交流社区:运维交流社区 欢迎大家的加入! 🐋 希望大家多多支…...
高效构建 vivo 企业级网络流量分析系统
作者:vivo 互联网服务器团队- Ming Yujia 随着网络规模的快速发展,网络状况的良好与否已经直接关系到了企业的日常收益,故障中的每一秒都会导致大量的用户流失与经济亏损。因此,如何快速发现网络问题与定位异常流量已经成为大型企…...

认识awk
awk 认识awk awk是一种编程语言,用于在linux/unix下对文本和数据进行处理。数据可以来自标准输入(stdin)、一个或多个文件,或其它命令的输出。它支持用户自定义函数和动态正则表达式等先进功能,是linux/unix下的一个强大编程工具。它在命令行…...

【C#学习笔记】数组和索引器
文章目录 数组单维数组多维数组交错数组 索引器类上的索引器方法1方法2 接口中的索引器 数组 数组具有以下属性: 数组可以是一维、多维或交错的。创建数组实例时,将建立纬度数量和每个纬度的长度。 这些值在实例的生存期内无法更改。数值数组元素的默认…...

常见距离计算的Python实现
常见的距离有曼哈顿距离、欧式距离、切比雪夫距离、闵可夫斯基距离、汉明距离、余弦距离等,用Python实现计算的方式有多种,可以直接构造公式计算,也可以利用内置线性代数函数计算,还可以利用scipy库计算。 1.曼哈顿距离 也叫城市…...
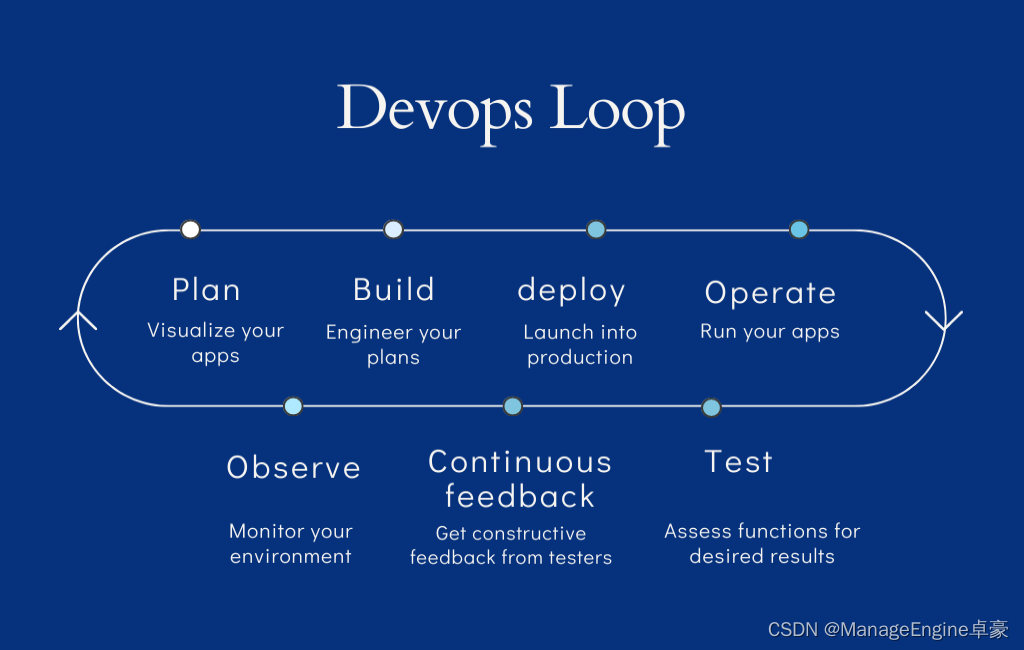
开发运营监控
DevOps 监控使管理员能够实时了解生产环境中的元素,并有助于确保应用程序平稳运行,同时提供最高的业务价值,对于采用 DevOps 文化和方法的公司来说,这一点至关重要。 什么是开发运营监控 DevOps 通过持续开发、集成、测试、监控…...

食品小程序的制作教程
在今天的互联网时代,小程序已经成为了各行业推广和销售的重要途径。特别是对于食品行业来说,拥有一个专属的小程序商城可以带来更多的用户和销售机会。那么,如何制作一个完美的食品小程序呢?下面就跟随我来一步步教你,…...
从入门到精通系列之十三:软件负载平衡选项)
Kubernetes(K8s)从入门到精通系列之十三:软件负载平衡选项
Kubernetes K8s从入门到精通系列之十三:软件负载平衡选项 一、软件负载平衡选项二、keepalived and haproxy三、keepalived配置四、haproxy配置五、选项 1:在操作系统上运行服务六、选项 2:将服务作为静态 Pod 运行 一、软件负载平衡选项 当…...
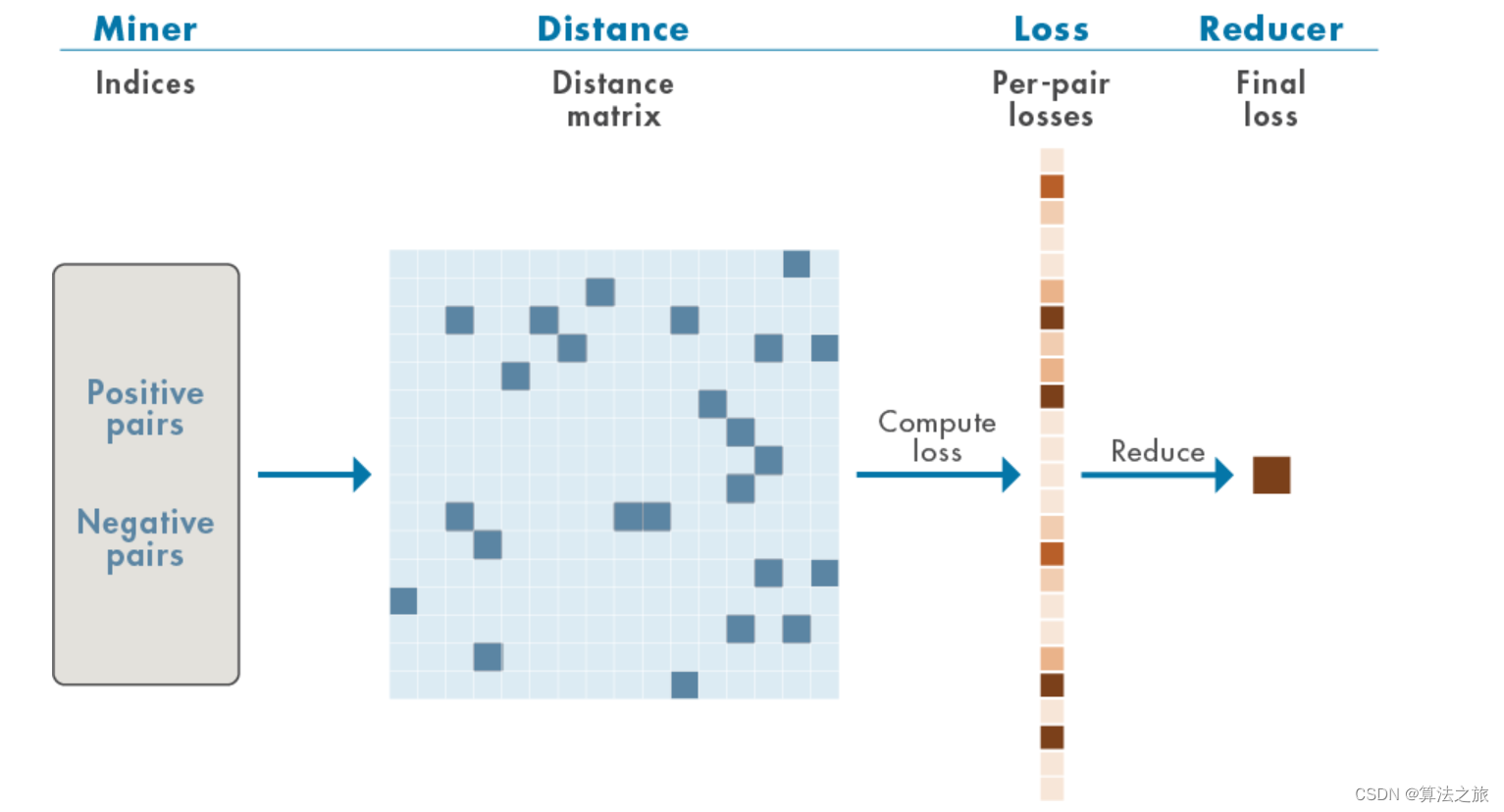
数据特征选择 | Matlab实现具有深度度量学习的时频特征嵌入
文章目录 效果一览文章概述源码设计参考资料效果一览 文章概述 数据特征选择 | Matlab实现具有深度度量学习的时频特征嵌入。 深度度量学习尝试学习非线性特征嵌入或编码器,它可以减少来自同一类的示例之间的距离(度量)并增加来自不同类的示例之间的距离。 以这种方式工作的…...

浅谈webpack
文章目录 Webpackwebpack的工作原理webpack的构建流程Webpack的基本功能有哪些Webpack常用配置 Webpack Webpack是一个现代的JavaScript应用程序静态模块打包工具。它是一个用于构建和打包前端资源的工具,可以将多个模块和资源(如JavaScript、CSS、图片…...

【 stable diffusion LORA模型训练最全最详细教程】
个人网站:https://tianfeng.space/ 文章目录 一、前言二、朱尼酱的赛博丹炉1.介绍2.解压配置3.使用训练准备首页设置上传素材查看进度 三、秋叶的lora训练器1.下载2.预处理3.参数调配 一、前言 其实想写LORA模型训练很久了,一直没时间,总结…...

蓝桥杯上岸每日N题 第八期 (全球变暖)!!!
蓝桥杯上岸每日N题第八期(全球变暖)!!! 同步收录 👇 蓝桥杯上岸必背!!!(第五期BFS) 大家好 我是寸铁💪 冲刺蓝桥杯省一模板大全来啦 🔥 蓝桥杯4月8号就要开始了 &am…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

C++ 设计模式 《小明的奶茶加料风波》
👨🎓 模式名称:装饰器模式(Decorator Pattern) 👦 小明最近上线了校园奶茶配送功能,业务火爆,大家都在加料: 有的同学要加波霸 🟤,有的要加椰果…...

基于Uniapp的HarmonyOS 5.0体育应用开发攻略
一、技术架构设计 1.混合开发框架选型 (1)使用Uniapp 3.8版本支持ArkTS编译 (2)通过uni-harmony插件调用原生能力 (3)分层架构设计: graph TDA[UI层] -->|Vue语法| B(Uniapp框架)B --&g…...

spring boot使用HttpServletResponse实现sse后端流式输出消息
1.以前只是看过SSE的相关文章,没有具体实践,这次接入AI大模型使用到了流式输出,涉及到给前端流式返回,所以记录一下。 2.resp要设置为text/event-stream resp.setContentType("text/event-stream"); resp.setCharacter…...


