常见距离计算的Python实现
常见的距离有曼哈顿距离、欧式距离、切比雪夫距离、闵可夫斯基距离、汉明距离、余弦距离等,用Python实现计算的方式有多种,可以直接构造公式计算,也可以利用内置线性代数函数计算,还可以利用scipy库计算。
1.曼哈顿距离
也叫城市街区距离,是两点差向量的L1范数,也就是各元素的绝对值之和。A(x1,x2,…,xn)和B(y1,y2,…,yn)之间的曼哈顿距离表示为
d = ∑ i = 1 n ∣ x i − y i ∣ d=\sum_{i=1}^{n}{\left| x_i-y_i \right|} d=i=1∑n∣xi−yi∣
Python实现:
import numpy as np
from scipy.spatial import distanceA = np.array([1,2,3])
B = np.array([4,5,6])# 方式一:直接构造公式计算
dist1 = np.sum(np.abs(A-B))# 方式二:内置线性代数函数计算
dist2 = np.linalg.norm(A-B,ord=1) #ord为范数类型,取值1(一范数),2(二范数),np.inf(无穷范数),默认2。# 方式三:scipy库计算
dist3 = distance.cityblock(A,B)2.欧式距离
是一种最常见的距离,也就是两点差向量的L2范数。A(x1,x2,…,xn)和B(y1,y2,…,yn)之间的欧式距离表示为
d = ∑ i = 1 n ( x i − y i ) 2 d=\sqrt{\sum_{i=1}^{n}{\left( x_i-y_i \right)^{2}}} d=i=1∑n(xi−yi)2
Python实现:
import numpy as np
from scipy.spatial import distanceA = np.array([1,2,3])
B = np.array([4,5,6])# 方式一:直接构造公式计算
dist1 = np.sqrt(np.sum((A-B)**2))# 方式二:内置线性代数函数计算
dist2 = np.linalg.norm(A-B,ord=2)# 方式三:scipy库计算
dist3 = distance.euclidean(A,B)3.切比雪夫距离
最大的维度内距离,是两点差向量的无穷范数。A(x1,x2,…,xn)和B(y1,y2,…,yn)之间的切比雪夫距离表示为
d = m a x ( ∣ x i − y i ∣ ) d=max\left( \left| x_i-y_i \right| \right) d=max(∣xi−yi∣)
Python实现:
import numpy as np
from scipy.spatial import distanceA = np.array([1,2,3])
B = np.array([4,5,6])# 方式一:直接构造公式计算
dist1 = np.max(np.abs(A-B))# 方式二:内置线性代数函数计算
dist2 = np.linalg.norm(A-B,ord=np.inf)# 方式三:scipy库计算
dist3 = distance.chebyshev(A,B)
4. 闵可夫斯基距离
是一种范式距离的统称,可表示为两点差向量的Lp范数。A(x1,x2,…,xn)和B(y1,y2,…,yn)之间的闵可夫斯基距离表示为
d = ∑ i = 1 n ∣ x i − y i ∣ p p d=\sqrt[p]{\sum_{i=1}^{n}{\left| x_i-y_i \right|^{p}}} d=pi=1∑n∣xi−yi∣p
Python实现:
import numpy as np
from scipy.spatial import distanceA = np.array([1,2,3])
B = np.array([4,5,6])# 方式一:内置线性代数函数计算
dist1 = np.linalg.norm(A-B,ord=3) # np.linalg.norm(A-B,ord=p)# 方式二:scipy库计算
dist2 = distance.minkowski(A,B,3) # distance.minkowski(A,B,p)5.汉明距离
衡量两个字符串之间的差异程度,对两个对象的向量元素逐个比较,差异的个数占总个数的比例。A(x1,x2,…,xn)和B(y1,y2,…,yn)之间的汉明距离表示为
d = 1 n ∑ i = 1 n I ( x i ≠ y i ) d=\frac{1}{n}\sum_{i=1}^{n}{I\left( x_i\ne y_i \right)} d=n1i=1∑nI(xi=yi)
其中I为指示函数,
I = { 1 i f ( x i ≠ y i ) 0 i f ( x i = y i ) \begin{equation} I= \left\{ \begin{array}{lr} 1 \quad if\left( x_i\ne y_i \right)&\\ 0 \quad if\left( x_i = y_i\right) \end{array} \right. \end{equation} I={1if(xi=yi)0if(xi=yi)
Python实现:
import numpy as np
from scipy.spatial import distanceA = np.array([1,2,3])
B = np.array([4,5,6])# 方式一:scipy库计算
dist1 = distance.hamming(A,B)
6.余弦距离
也叫余弦相似度,是两点空间向量夹角的余弦值,是内积与模积的比值,用来衡量两向量间的差异程度。A(x1,x2,…,xn)和B(y1,y2,…,yn)之间的余弦距离表示为
d = c o s θ = < A , B > ∣ A ∣ ⋅ ∣ B ∣ = ∑ i = 1 n x i y i ∑ i = 1 n x i 2 ⋅ ∑ i = 1 n y i 2 \begin{align} d&=cos\theta=\frac{<A,B>}{\left| A \right|\cdot\left| B \right|} \\ &=\frac{\sum_{i=1}^{n}{x_iy_i}}{\sqrt{\sum_{i=1}^{n}{x_i^{2}}}\cdot\sqrt{\sum_{i=1}^{n}{y_i^{2}}}} \end{align} d=cosθ=∣A∣⋅∣B∣<A,B>=∑i=1nxi2⋅∑i=1nyi2∑i=1nxiyi
Python实现:
import numpy as np
from scipy.spatial import distanceA = np.array([1,2,3])
B = np.array([4,5,6])# 方式一:直接构造公式计算
dist1 = np.sum(A*B)/(np.sqrt(np.sum(A**2))*np.sqrt(np.sum(B**2)))# 方式二:scipy库计算
dist2 = 1-distance.cosine(A,B)
End.
参考:
https://blog.csdn.net/lemonbit/article/details/129053257
相关文章:

常见距离计算的Python实现
常见的距离有曼哈顿距离、欧式距离、切比雪夫距离、闵可夫斯基距离、汉明距离、余弦距离等,用Python实现计算的方式有多种,可以直接构造公式计算,也可以利用内置线性代数函数计算,还可以利用scipy库计算。 1.曼哈顿距离 也叫城市…...
开发运营监控
DevOps 监控使管理员能够实时了解生产环境中的元素,并有助于确保应用程序平稳运行,同时提供最高的业务价值,对于采用 DevOps 文化和方法的公司来说,这一点至关重要。 什么是开发运营监控 DevOps 通过持续开发、集成、测试、监控…...

食品小程序的制作教程
在今天的互联网时代,小程序已经成为了各行业推广和销售的重要途径。特别是对于食品行业来说,拥有一个专属的小程序商城可以带来更多的用户和销售机会。那么,如何制作一个完美的食品小程序呢?下面就跟随我来一步步教你,…...
从入门到精通系列之十三:软件负载平衡选项)
Kubernetes(K8s)从入门到精通系列之十三:软件负载平衡选项
Kubernetes K8s从入门到精通系列之十三:软件负载平衡选项 一、软件负载平衡选项二、keepalived and haproxy三、keepalived配置四、haproxy配置五、选项 1:在操作系统上运行服务六、选项 2:将服务作为静态 Pod 运行 一、软件负载平衡选项 当…...
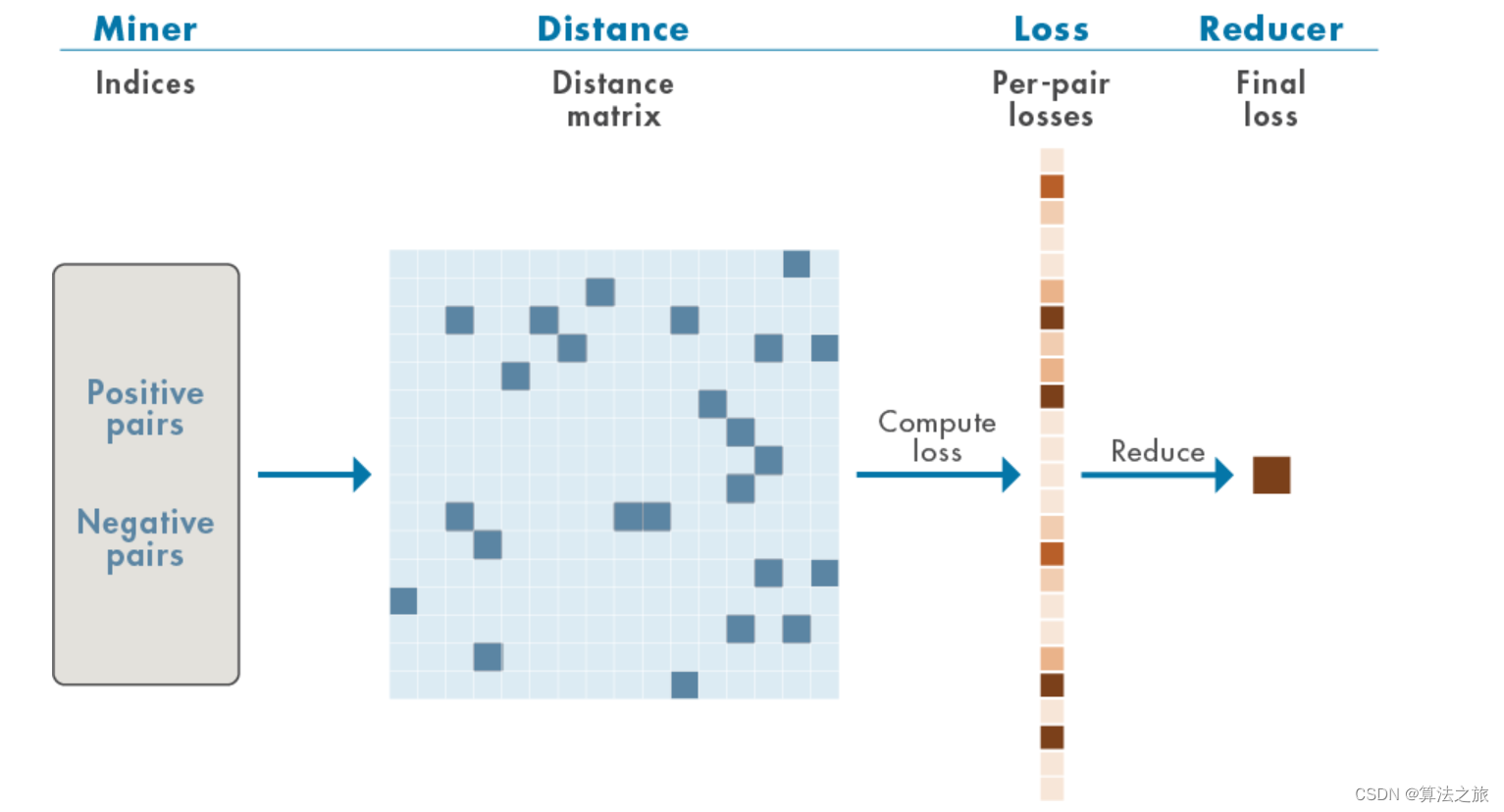
数据特征选择 | Matlab实现具有深度度量学习的时频特征嵌入
文章目录 效果一览文章概述源码设计参考资料效果一览 文章概述 数据特征选择 | Matlab实现具有深度度量学习的时频特征嵌入。 深度度量学习尝试学习非线性特征嵌入或编码器,它可以减少来自同一类的示例之间的距离(度量)并增加来自不同类的示例之间的距离。 以这种方式工作的…...

浅谈webpack
文章目录 Webpackwebpack的工作原理webpack的构建流程Webpack的基本功能有哪些Webpack常用配置 Webpack Webpack是一个现代的JavaScript应用程序静态模块打包工具。它是一个用于构建和打包前端资源的工具,可以将多个模块和资源(如JavaScript、CSS、图片…...

【 stable diffusion LORA模型训练最全最详细教程】
个人网站:https://tianfeng.space/ 文章目录 一、前言二、朱尼酱的赛博丹炉1.介绍2.解压配置3.使用训练准备首页设置上传素材查看进度 三、秋叶的lora训练器1.下载2.预处理3.参数调配 一、前言 其实想写LORA模型训练很久了,一直没时间,总结…...

蓝桥杯上岸每日N题 第八期 (全球变暖)!!!
蓝桥杯上岸每日N题第八期(全球变暖)!!! 同步收录 👇 蓝桥杯上岸必背!!!(第五期BFS) 大家好 我是寸铁💪 冲刺蓝桥杯省一模板大全来啦 🔥 蓝桥杯4月8号就要开始了 &am…...
CSS基础介绍笔记1
官方文档 CSS指的是层叠样式(Cascading Style Sheets)地址:CSS 教程离线文档:放大放小:ctrl鼠标滚动为什么需要css:简化修改HTML元素的样式;将html页面的内容与样式分离提高web开发的工作效率&…...
:如何快速解决项目中问题?)
https请求异常引发(Received fatal alert: unrecognized_name):如何快速解决项目中问题?
总结思考:如何做一个出色的开发者? 首先我们要承认我们大部分程序员是应用开发,不是操作系统、协议、框架开发等这类底层开发者。 其一:是否能快速定位问题。如找到出现问题的代码,bug出现在哪一行,哪个应…...

小程序 view下拉滑动导致scrollview滑动事件失效
小程序页面需要滑动功能 下拉时滑动,展示整个会员卡内容, 下拉view里包含了最近播放:有scrollview,加了下拉功能后,scrollview滑动失败了。 <view class"cover-section" catchtouchstart"handletou…...

《ROS2》教程
参考资料: 古月居 B站视频: https://www.bilibili.com/video/BV16B4y1Q7jQ/?spm_id_from333.999.0.0 对应资料:https://book.guyuehome.com/ ROS之前最好有点ROS1的基础,跳转门:ROS-https://www.bilibili.com/video/B…...

抖音seo源码开发源代码搭建分享
抖音SEO源码开发涉及到以下几个方面: 前端开发:包括抖音SEO页面的设计与布局,以及需要使用到的前端技术,如HTML、CSS、JavaScript等。 后端开发:包括抖音SEO页面的数据获取和处理,以及需要使用到的后端技术…...

MATLAB——使用建立好的神经网络进行分类程序
学习目标:使用建立好的神经网络(训练好并保存,下次直接调用该神经网络)进行分类 clear all; close all; P[-0.4 -0.4 0.5 -0.2 -0.7;-0.6 0.6 -0.4 0.3 0.8]; %输入向量 T[1 1 0 0 1]; …...
Spring5.2.x 源码使用Gradle成功构建
一 前置准备 1 Spring5.2.x下载 1.1 Spring5.2.x Git下载地址 https://gitcode.net/mirrors/spring-projects/spring-framework.git 1.2 Spring5.2.x zip源码包下载,解压后倒入idea https://gitcode.net/mirrors/spring-projects/spring-framework/-/…...

iOS永久签名工具 - 轻松签使用教程
轻松签是一款IOS端免费的IPA签名和安装工具,最新版可以不用依赖证书对ipa永久签名,虽然现在用上了巨魔(TrollStore)- 是国外iOS开发人员opa334dev发布的一款工具,可以在不越狱的情况下,安装任何一款APP。 …...
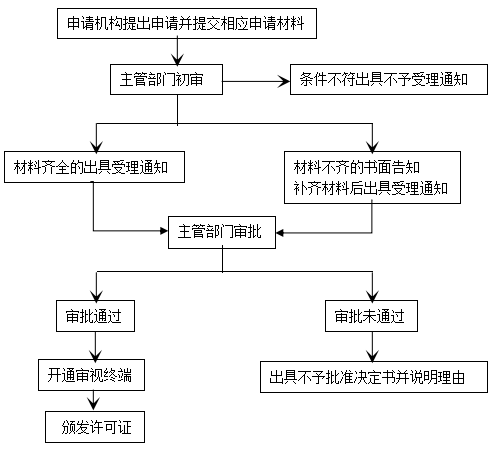
如何申请中国境内提供金融信息服务业务许可
依据《外国机构在中国境内提供金融信息服务管理规定》《外国机构在中国境内提供金融信息服务申请许可说明》等政策,外国机构在中国境内提供金融信息服务业务许可要求如下: 金融信息服务定义 所称的外国机构,是指外国金融信息服务提供者。 …...
)
Java多线程(六)
目录 一、什么是线程安全问题 二、产生线程安全问题的原因 三、解决线程安全问题的方法 3.1 join()等待 3.2 synchronized加锁 3.3 wait()和notify() 3.4 volatile关键字 一、什么是线程安全问题 在操作系统中,线程的调度是随机的(抢占式执行࿰…...

ceil(),floor(),round()函数C++详解
ceil() ceil()函数是这样的: double ceil(double x) ceil函数可以把x上取整。 例子: #include <bits/stdc.h> using namespace std; int main() {double a, b;cin >> a >> b;printf("ceil(%.2f) %.2…...
自动化处理,web自动化测试处理多窗口+切换iframe框架页总结(超细整理)
目录:导读 前言一、Python编程入门到精通二、接口自动化项目实战三、Web自动化项目实战四、App自动化项目实战五、一线大厂简历六、测试开发DevOps体系七、常用自动化测试工具八、JMeter性能测试九、总结(尾部小惊喜) 前言 web 自动化之处理…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...

Python 高效图像帧提取与视频编码:实战指南
Python 高效图像帧提取与视频编码:实战指南 在音视频处理领域,图像帧提取与视频编码是基础但极具挑战性的任务。Python 结合强大的第三方库(如 OpenCV、FFmpeg、PyAV),可以高效处理视频流,实现快速帧提取、压缩编码等关键功能。本文将深入介绍如何优化这些流程,提高处理…...
)
华为OD最新机试真题-数组组成的最小数字-OD统一考试(B卷)
题目描述 给定一个整型数组,请从该数组中选择3个元素 组成最小数字并输出 (如果数组长度小于3,则选择数组中所有元素来组成最小数字)。 输入描述 行用半角逗号分割的字符串记录的整型数组,0<数组长度<= 100,0<整数的取值范围<= 10000。 输出描述 由3个元素组成…...
:LeetCode 142. 环形链表 II(Linked List Cycle II)详解)
Java详解LeetCode 热题 100(26):LeetCode 142. 环形链表 II(Linked List Cycle II)详解
文章目录 1. 题目描述1.1 链表节点定义 2. 理解题目2.1 问题可视化2.2 核心挑战 3. 解法一:HashSet 标记访问法3.1 算法思路3.2 Java代码实现3.3 详细执行过程演示3.4 执行结果示例3.5 复杂度分析3.6 优缺点分析 4. 解法二:Floyd 快慢指针法(…...

【51单片机】4. 模块化编程与LCD1602Debug
1. 什么是模块化编程 传统编程会将所有函数放在main.c中,如果使用的模块多,一个文件内会有很多代码,不利于组织和管理 模块化编程则是将各个模块的代码放在不同的.c文件里,在.h文件里提供外部可调用函数声明,其他.c文…...

从0开始学习R语言--Day17--Cox回归
Cox回归 在用医疗数据作分析时,最常见的是去预测某类病的患者的死亡率或预测他们的结局。但是我们得到的病人数据,往往会有很多的协变量,即使我们通过计算来减少指标对结果的影响,我们的数据中依然会有很多的协变量,且…...
