leetcode410. 分割数组的最大值 动态规划
-
hard:https://leetcode.cn/problems/split-array-largest-sum/
-
给定一个非负整数数组 nums 和一个整数 m ,
你需要将这个数组分成 m 个非空的连续子数组。 -
设计一个算法使得这
m 个子数组各自和的最大值最小。
示例 1:输入:nums = [7,2,5,10,8], m = 2
输出:18
解释:
一共有四种方法将 nums 分割为 2 个子数组。
其中最好的方式是将其分为 [7,2,5] 和 [10,8] 。
因为此时这两个子数组各自的和的最大值为18,在所有情况中最小。
示例 2:输入:nums = [1,2,3,4,5], m = 2
输出:9
示例 3:输入:nums = [1,4,4], m = 3
输出:4提示:1 <= nums.length <= 1000
0 <= nums[i] <= 106
1 <= m <= min(50, nums.length)
题解
-
令 dp[i][j]表示将数组的
前 i 个数分割为 j 组所能得到的最大连续子数组和的最小值 -
确定装填转移方程(考虑dp[i][j]需要遍历所有分为j-1组的情况):
d p [ i ] [ j ] = m i n k = 0 i − 1 { m a x ( d p [ k ] [ j − 1 ] , s u b ( k + 1 , i ) ) } = m i n k = 0 i − 1 { m a x ( d p [ k ] [ j − 1 ] , s u m ( n u m s [ k + 1 … j ] ) ) } dp[i][j]= min_{k=0}^{ i−1} \{max(dp[k][j−1],sub(k+1,i))\}\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ = min_{k=0}^{ i−1} \{max(dp[k][j−1],sum(nums[k+1…j]))\} dp[i][j]=mink=0i−1{max(dp[k][j−1],sub(k+1,i))} =mink=0i−1{max(dp[k][j−1],sum(nums[k+1…j]))} -
确定边界:填表法
nums = [7,2,5,10,8],m=2。
| i\j | 0 | 1 | 2 |
|---|---|---|---|
| 0 | 无法分为0组 | INT_MAX | INT_MAX |
| 1 | 无法分为0组 | 7 | 1个数无法分为2组(i<j) |
| 2 | 无法分为0组 | 7+2 | m i n ( [ 7 ] , [ 2 ] ) = 2 min([7],[2])=2 min([7],[2])=2 |
| 3 | 无法分为0组 | 7+2+5 | m i n [ m a x ( d p [ 1 ] [ 1 ] , [ 2 , 5 ] ) m a x ( d p [ 2 ] [ 1 ] , [ 5 ] ) ] = 7 min\begin{bmatrix} max(dp[1][1],[2,5]) \\ max(dp[2][1],[5]) \end{bmatrix}=7 min[max(dp[1][1],[2,5])max(dp[2][1],[5])]=7 |
| 4 | 无法分为0组 | 7+2+5+10 | m i n [ m a x ( d p [ 1 ] [ 1 ] , [ 2 , 5 , 10 ] ) m a x ( d p [ 2 ] [ 1 ] , [ 5 , 10 ] ) m a x ( d p [ 3 ] [ 1 ] , [ 10 ] ) ] = 14 min\begin{bmatrix} max(dp[1][1],[2,5,10]) \\ max(dp[2][1],[5,10]) \\ max(dp[3][1],[10]) \end{bmatrix}=14 min max(dp[1][1],[2,5,10])max(dp[2][1],[5,10])max(dp[3][1],[10]) =14 前*个数分为一组和剩下的部分 |
| 5 | 无法分为0组 | 7+2+5+10+8 | m i n [ m a x ( d p [ 1 ] [ 1 ] , [ 2 , 5 , 10 , 8 ] ) m a x ( d p [ 2 ] [ 1 ] , [ 5 , 10 , 8 ] ) m a x ( d p [ 3 ] [ 1 ] , [ 10 , 8 ] ) m a x ( d p [ 4 ] [ 1 ] , [ 8 ] ) ] = 18 min\begin{bmatrix} max(dp[1][1],[2,5,10,8]) \\ max(dp[2][1],[5,10,8]) \\ max(dp[3][1],[10,8])\\ max(dp[4][1],[8]) \end{bmatrix}=18 min max(dp[1][1],[2,5,10,8])max(dp[2][1],[5,10,8])max(dp[3][1],[10,8])max(dp[4][1],[8]) =18 |
code
class Solution {
public:int splitArray(vector<int>& nums, int m) {int n = nums.size();vector<vector<long long>> dp(n + 1, vector<long long>(m + 1, LLONG_MAX));vector<long long> sub(n + 1, 0);for (int i = 0; i < n; i++) {sub[i + 1] = sub[i] + nums[i];}dp[0][0] = 0;for (int i = 1; i <= n; i++) {for (int j = 1; j <= min(i, m); j++) {for (int k = 0; k < i; k++) {dp[i][j] = min(dp[i][j], max(dp[k][j - 1], sub[i] - sub[k]));}}}return (int)dp[n][m];}
};相关文章:

leetcode410. 分割数组的最大值 动态规划
hard:https://leetcode.cn/problems/split-array-largest-sum/ 给定一个非负整数数组 nums 和一个整数 m ,你需要将这个数组分成 m 个非空的连续子数组。 设计一个算法使得这 m 个子数组各自和的最大值最小。 示例 1:输入:nums [7,2,5,1…...

C函数指针与类型定义
#include <stdio.h> #define PI 3.14 typedef int uint32_t; /* pfun is a pointer and its type is void (*)(void) */ void (*pfun)(void); /* afer typedef like this we can use “pfun1” as a data type to a function that has form like: / -------…...

最新2024届【海康威视】内推码【GTK3B6】
最新2024届【海康威视】内推码【GTK3B6】 【内推码使用方法】 1.请学弟学妹们登录校招官网,选择岗位投递简历; 2.投递过程中填写内推码完成内推步骤,即可获得内推特权。 内推码:GTK3B6 内推码:GTK3B6 内推码&…...

边写代码边学习之LSTM
1. 什么是LSTM 长短期记忆网络 LSTM(long short-term memory)是 RNN 的一种变体,其核心概念在于细胞状态以及“门”结构。细胞状态相当于信息传输的路径,让信息能在序列连中传递下去。你可以将其看作网络的“记忆”。理论上讲&a…...
)
Elasticsearch8.8.0 SpringBoot实战操作各种案例(索引操作、聚合、复杂查询、嵌套等)
Elasticsearch8.8.0 全网最新版教程 从入门到精通 通俗易懂 配置项目 引入依赖 <dependency><groupId>cn.hutool</groupId><artifactId>hutool-all</artifactId><version>5.8.16</version></dependency><dependency>&l…...
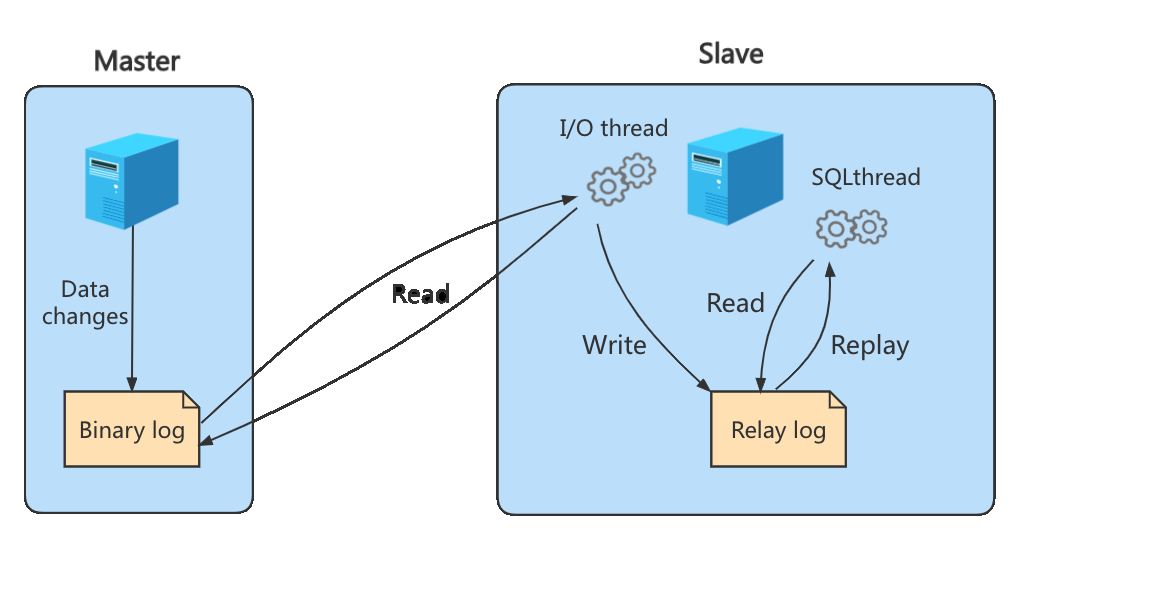
《MySQL高级篇》十五、其他数据库日志
文章目录 1. MySQL支持的日志1.1 日志类型1.2 日志的弊端 2. 慢查询日志(slow query log)3. 通用查询日志3.1 问题场景3.2 查看当前状态3.3 启动日志3.4 查看日志3.5 停止日志3.6 删除\刷新日志 4. 错误日志(error log)4.1 启动日志4.2 查看日志4.3 删除\刷新日志4.4 MySQL8.0新…...

【Linux】【预】配置虚拟机的桥接网卡+nfs
【Linux】【预】配置虚拟机的桥接网卡 1. 配置VM虚拟机的桥接网络2 配置Win10中的设置3.配置Linux中的IP4. 串口连接开发板,配置nfs5 修改网络文件6 验证nfs 是否成功总结 1. 配置VM虚拟机的桥接网络 右击设置,选择添加网络,按照如下顺序操作…...

【Android】Retrofit2和RxJava2新手快速上手
写这篇博客的目的 网上关于Retrofit2和RxJava2的博客特别多,但是内容特别复杂,一上来就讲解很高级的用法 其实我们没必要像高考做题家一样,把每个API都背的滚瓜烂熟 熟悉基本用法,高阶用法需要的时候再逐个了解就行了 因为博客…...

1.4 Nacos注册中心
目录 什么是Nacos Nacos下载和安装 下载和安装 启动 Nacos服务注册与发现 Nacos的服务分级存储模型 什么是分级存储模型 配置实例集群 配置同集群优先的负载均衡 权重配置 点击编辑按钮 配置所需的权重 环境隔离 创建namespace 什么是Nacos Nacoshttps://nacos.i…...

AOJ 2200 Mr. Rito Post Office 最短路径+动态规划+谨慎+思维
我写了好多注释,一看就能看懂,这个题目我想了6,7个小时,一开始忽略了船的位置和要把船安置的位置一致的情况,补上就对了。 #include <iostream> using namespace std; int inf 0x3f3f3f3f, num[1007], dp[1007…...

红米电视 ADB 安装 app 报错 failed to authenticate xxx:5555
开启电视开发者模式,允许安装未知来源应用及开启 ADB 调试电脑端下载 adb 工具 点击下载同一局域网的电脑使用 adb 工具连接(提前查看电视 IP)D:\adb>adb connect 192.168.1.7 * daemon not running; starting now at tcp:5037 * daemon s…...

Linux 下设置开机自启动的方法
文章目录 事先准备对于普通的 Linux对于 RedHat Enterprise Linux 9 笔者的运行环境: 设置成功过的 Linux: RedHat Enterprise Linux 9 x86_64 CentOS 8 x86_64 事先准备 进行这个教程之前,必须要先安装好一个 Linux 操作系统。这个 Linux…...
MySQL常见问题处理(三)
MySQL 常见问题解决 夕阳留恋的不是黄昏,而是朝阳 上一章简单介绍了MySQL数据库安装(二), 如果没有看过, 请观看上一章 一. root 用户密码忘记,进行重置操作 复制内容来源链接: https://blog.csdn.net/weixin_48927364/article/details/123556927 一.…...

maven中常见问题
文章目录 一、配置项提示二、父子打包三、打包之后不显示target四、自定义打包之后的jar包名称五、整个项目打包5.1、父项目管理插件和微服务打包 一、配置项提示 SpringBoot中提示错误信息 表示的是SpringBoot中的注释提示没有配置!那么可以来使用一下springboot官…...

vue2中bus的使用
说明:为了解决组件间的通信,也就是组件与组件间的数据传递(它们之间毫无关系); 这里以组件1传递数据到组件2为例 1.首先新建一个Bus.js文件 import Vue from vue const Bus new Vue() export default Bus 2.在组件1中引用 传递数据 imp…...

实证研究在机器学习中的应用
实证研究是一种基于实际数据和事实的科学研究方法,目的是通过观察、测量、分析和解释数据来验证或否定某个假设、理论或研究问题。这种研究方法通常用于社会科学、自然科学和医学等领域。以下是实证研究的详细解释: 研究目标:实证研究旨在通过…...

IO进程线程day8(2023.8.6)
一、Xmind整理: 管道的原理: 有名管道的特点: 信号的原理: 二、课上练习: 练习1:pipe 功能:创建一个无名管道,同时打开无名管道的读写端 原型: #include <unist…...

【5G NR】逻辑信道、传输信道和物理信道的映射关系
博主未授权任何人或组织机构转载博主任何原创文章,感谢各位对原创的支持! 博主链接 本人就职于国际知名终端厂商,负责modem芯片研发。 在5G早期负责终端数据业务层、核心网相关的开发工作,目前牵头6G算力网络技术标准研究。 博客…...

tmux基础教程
tmux基础教程 Mac安装 brew install tmuxubuntu安装 sudo apt-get install tmux入门使用 会话 (Session) Ctrlb d: 分离当前会话。Ctrlb s: 列出所有会话。Ctrlb $: 重命名当前会话。 窗口(Window) Ctrlb c: 创建一个新窗口, 状态栏会显示多个窗…...
项目实战 — 消息队列(4){消息持久化}
目录 一、消息存储格式设计 🍅 1、queue_data.txt:保存消息的内容 🍅 2、queue_stat.txt:保存消息的统计信息 二、消息序列化 三、自定义异常类 四、创建MessageFileManger类 🍅 1、约定消息文件所在的目录和文件名…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...

go 里面的指针
指针 在 Go 中,指针(pointer)是一个变量的内存地址,就像 C 语言那样: a : 10 p : &a // p 是一个指向 a 的指针 fmt.Println(*p) // 输出 10,通过指针解引用• &a 表示获取变量 a 的地址 p 表示…...

pycharm 设置环境出错
pycharm 设置环境出错 pycharm 新建项目,设置虚拟环境,出错 pycharm 出错 Cannot open Local Failed to start [powershell.exe, -NoExit, -ExecutionPolicy, Bypass, -File, C:\Program Files\JetBrains\PyCharm 2024.1.3\plugins\terminal\shell-int…...

C++实现分布式网络通信框架RPC(2)——rpc发布端
有了上篇文章的项目的基本知识的了解,现在我们就开始构建项目。 目录 一、构建工程目录 二、本地服务发布成RPC服务 2.1理解RPC发布 2.2实现 三、Mprpc框架的基础类设计 3.1框架的初始化类 MprpcApplication 代码实现 3.2读取配置文件类 MprpcConfig 代码实现…...
