【数据结构】二叉树 链式结构的相关问题
本篇文章来详细介绍一下二叉树链式结构经常使用的相关函数,以及相关的的OJ题。
目录
1.前置说明
2.二叉树的遍历
2.1 前序、中序以及后序遍历
2.2 层次遍历
3.节点个数相关函数实现
3.1 二叉树节点个数
3.2 二叉树叶子节点个数
3.3 二叉树第k层节点个数
3.4 在二叉树中查找值为x的节点
4.二叉树基础oj练习
5.二叉树的创建和销毁
5.1 通过前序遍历构建二叉树
5.2 销毁二叉树
5.3 判断二叉树是否为完全二叉树
1.前置说明
在学习链式二叉树的基本操作前,需先要创建一棵二叉树,然后才能学习其相关的基本操作。由于现在大家对二叉树结构掌握还不够深入,为了降低大家学习成本,此处手动快速创建一棵简单的二叉树,快速进入二叉树操作学习,等二叉树结构了解的差不多时,我们反过头再来研究二叉树真正的创建方式。
typedef int BTDataType;typedef struct BinaryTreeNode
{BTDataType data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}BTNode;//创造树节点
BTNode* BuyNode(BTDataType x)
{BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));if (newnode == NULL){perror("malloc fail");return NULL;} newnode->data = x;newnode->left = newnode->right = NULL;return newnode;
}// 构建二叉树
BTNode* CreatBinaryTree()
{BTNode* node1 = BuyNode(1);BTNode* node2 = BuyNode(2);BTNode* node3 = BuyNode(3);BTNode* node4 = BuyNode(4);BTNode* node5 = BuyNode(5);BTNode* node6 = BuyNode(6);node1->Left = node2;node1->Right = node4;node2->Left = node3;node4->Right = node5;node4->Left = node6;return node1;
}注意:上述代码并不是创建二叉树的方式,真正创建二叉树方式后面详解重点讲解。
再看二叉树基本操作前,再回顾下二叉树的概念,二叉树是:
- 空树
- 非空:根节点,根节点的左子树、根节点的右子树组成的。
创建的二叉树图解:
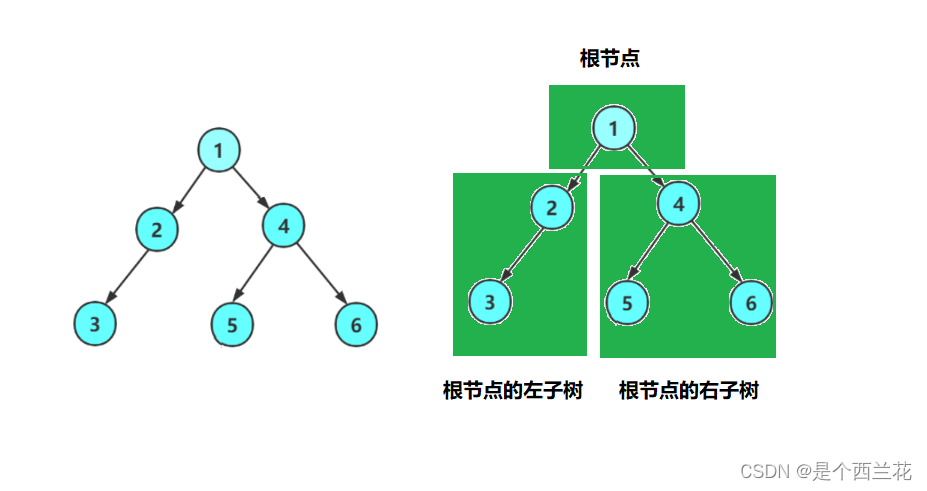
从概念中可以看出,二叉树定义是递归式的,因此后序基本操作中基本都是按照该概念实现的。
2.二叉树的遍历
2.1 前序、中序以及后序遍历
学习二叉树结构,最简单的方式就是遍历。所谓二叉树遍历(Traversal)是按照某种特定的规则,依次对二叉树中的节点进行相应的操作,并且每个节点只操作一次。访问结点所做的操作依赖于具体的应用问题。遍历是二叉树上最重要的运算之一,也是二叉树上进行其它运算的基础。
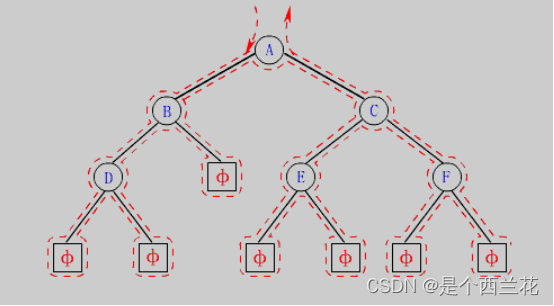
按照规则,二叉树的遍历有:前序/中序/后序的递归结构遍历:
- 前序遍历(Preorder Traversal亦称先序遍历)――访问根结点的操作发生在遍历其左右子树之前。
- 中序遍历(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中(间)。
- 后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。
由于被访问的结点必是某子树的根,所以N(Node)、L(Left subtree)和R(Right subtree)又可解释为根、根的左子树和根的右子树。NLR、LNR和LRN分别又称为先根遍历、中根遍历和后根遍历。
// 二叉树前序遍历
void BinaryTreePrevOrder(BTNode* root);
// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root);
// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root);三个函数实现起来非常相似,只是访问数据的顺序不同。
具体实现:
// 二叉树前序遍历
void BinaryTreePrevOrder(BTNode* root)
{if (root==NULL){printf("# ");return;}printf("%c ",root->data);BinaryTreePrevOrder(root->left);BinaryTreePrevOrder(root->right);
}
// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root)
{if (root == NULL){printf("#");return;}BinaryTreePrevOrder(root->left);printf("%c ", root->data);BinaryTreePrevOrder(root->right);
}
// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root)
{if (root == NULL){printf("#");return;}BinaryTreePrevOrder(root->left);BinaryTreePrevOrder(root->right);printf("%c ", root->data);
}下面主要分析前序递归遍历,中序与后序图解类似,大家可自己动手绘制。
前序遍历递归图解:
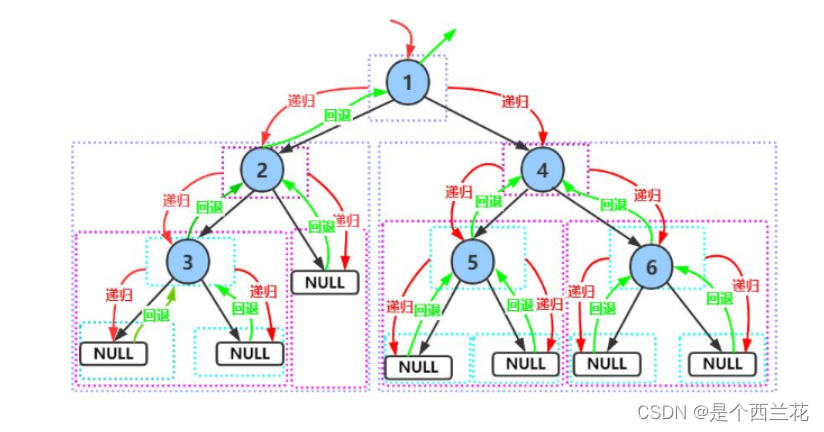
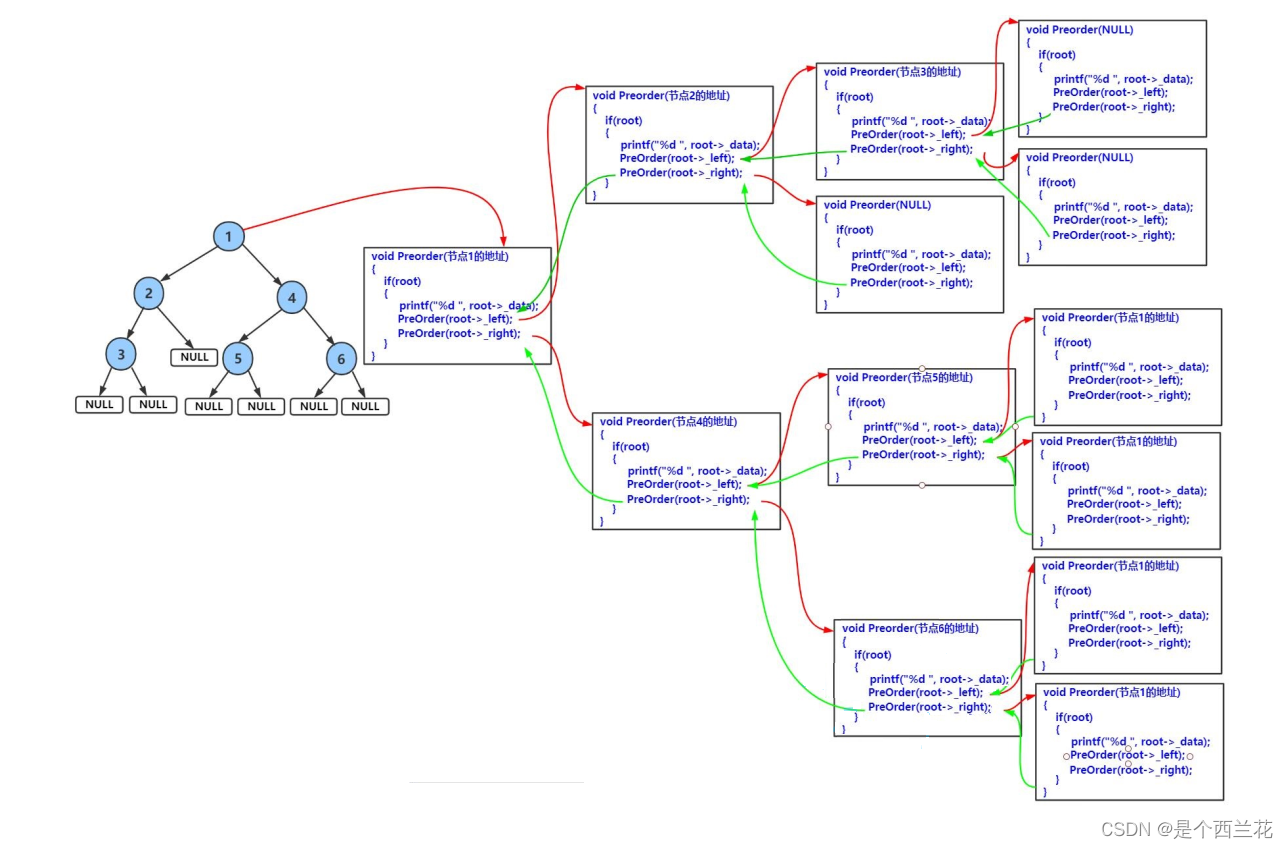
前序遍历结果:1 2 3 4 5 6
中序遍历结果:3 2 1 5 4 6
后序遍历结果:3 2 5 6 4 1
2.2 层次遍历
层序遍历:除了先序遍历、中序遍历、后序遍历外,还可以对二叉树进行层序遍历。设二叉树的根节点所在层数为1,层序遍历就是从所在二叉树的根节点出发,首先访问第一层的树根节点,然后从左到右访问第2层上的节点,接着是第三层的节点,以此类推,自上而下,自左至右逐层访问树的结点的过程就是层序遍历。
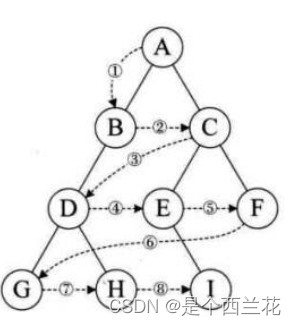
那么我们怎么实现呢?
这里需要使用队列,让根节点先入堆,再出队,出队时让左右子树入堆,空树不进队,按照这个方式可以实现二叉树的层次遍历。
具体实现:这里队列相关函数要自己实现,C++就方便多了,以后会讲。
// 层序遍历
void BinaryTreeLevelOrder(BTNode* root)
{//创建一个队列Queue q;//初始化队列QueueInit(&q);if (root)QueuePush(&q, root);while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);printf("%c ", front->data);if (front->left){QueuePush(&q, front->left);}if (front->right){QueuePush(&q, front->right);}}printf("\n");QueueDestroy(&q);
}3.节点个数相关函数实现
3.1 二叉树节点个数
=左子树的节点数+右子树的节点数+根节点数。根节点数为1。
// 二叉树节点个数
int BinaryTreeSize(BTNode* root)
{if (root == NULL){return 0;}return BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
}3.2 二叉树叶子节点个数
=左子树的叶子节点数+右子树的叶子节点数。
// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root)
{if (root == NULL){return 0;}if (root->right == NULL && root->left == NULL){return 1;}return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}3.3 二叉树第k层节点个数
=左子树的K-1层节点数+右子树的K-1层节点数。
// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{assert(k > 0);if (root == NULL){return 0;}if (k == 1){return 1;}return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
}3.4 在二叉树中查找值为x的节点
=根节点不是,就在左子树和右子树中寻找
//在二叉树中查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{if (root == NULL){return NULL;}if (root->data == x){return root;}BTNode* left = BinaryTreeFind(root->left, x);BTNode* right = BinaryTreeFind(root->right, x);return left == NULL ? right : left;
}4.二叉树基础oj练习
- 单值二叉树。OJ链接
- 检查两颗树是否相同。OJ链接
- 对称二叉树。OJ链接
- 二叉树的前序遍历。OJ链接
- 二叉树中序遍历。OJ链接
- 二叉树的后序遍历。OJ链接
- 另一颗树的子树。OJ链接
5.二叉树的创建和销毁
二叉树的构建及遍历。OJ链接
5.1 通过前序遍历构建二叉树
通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树,'#'代表空。
代码实现:
//开辟树节点空间
BTNode* BuyNode(char x)
{BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));newnode->data = x;newnode->left = newnode->right = NULL;return newnode;
}
//构建树
BTNode* CreatTree(char* arr,int*i)
{if(arr[*i] =='#'){(*i)++;return NULL;}BTNode* node = BuyNode(arr[*i]);(*i)++;node->left = CreatTree(arr,i);node->right = CreatTree(arr,i);return node;
}int main()
{char arr[] = "ABD##E#H##CF##G##";int i = 0;//传递下标的地址,这样就可以通过地址修改下标。BTNode* tree = CreatTree(arr, &i);return 0;
}5.2 销毁二叉树
这里是后序思想,先释放左右子树,最后释放根节点。
// 二叉树销毁
void BinaryTreeDestory(BTNode** root)
{if (*root == NULL){return;}BinaryTreeDestory(&((*root)->left));BinaryTreeDestory(&((*root)->right)); free(*root);*root = NULL;
}5.3 判断二叉树是否为完全二叉树
这里也是通过队列进行判断,之前层次遍历空树不进队,而这里空树进队,当出队时遇到空时,停止出队,判断队列中是否有非空,如果有就不是完全二叉树。
代码实现:
// 判断二叉树是否是完全二叉树
int BinaryTreeComplete(BTNode* root)
{Queue q;QueueInit(&q);if (root)QueuePush(&q, root);while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);if (front != NULL){QueuePop(&q);QueuePush(&q, front->left);QueuePush(&q, front->right);}else{//遇到空就跳出break;}}//检查后面节点有没有非空//有非空就不是完全二叉树while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);if (front != NULL) return 0;//不是}return 1;//是
}本篇结束!
相关文章:

【数据结构】二叉树 链式结构的相关问题
本篇文章来详细介绍一下二叉树链式结构经常使用的相关函数,以及相关的的OJ题。 目录 1.前置说明 2.二叉树的遍历 2.1 前序、中序以及后序遍历 2.2 层次遍历 3.节点个数相关函数实现 3.1 二叉树节点个数 3.2 二叉树叶子节点个数 3.3 二叉树第k层节点个数 3…...
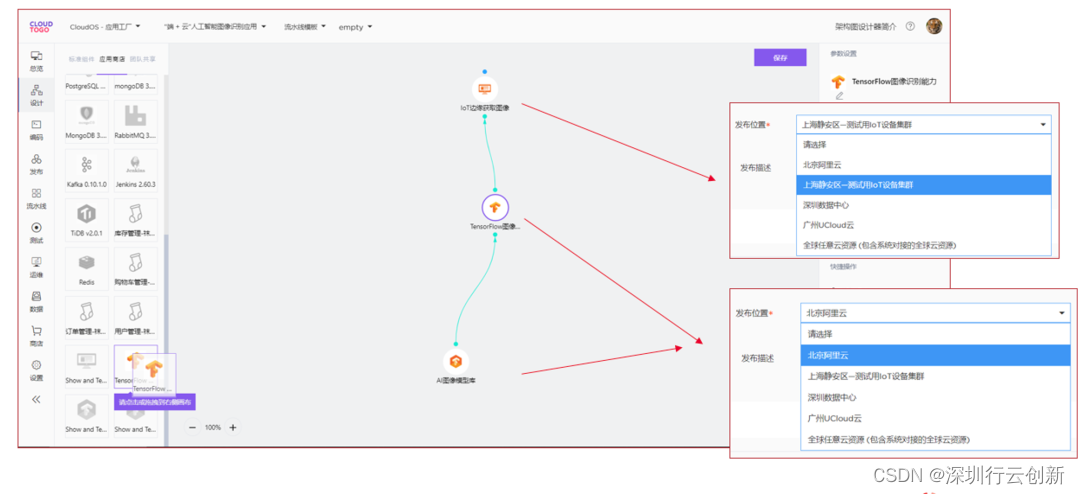
【无标题】云原生在工业互联网的落地及好处!
什么是工业互联网? 工业互联网(Industrial Internet)是新一代信息通信技术与工业经济深度融合的新型基础设施、应用模式和工业生态,通过对人、机、物、系统等的全面连接,构建起覆盖全产业链、全价值链的全新制造和服务…...

人工智能在心电信号分类中的应用
目录 1 引言 2 传统机器学习中的特征提取与选择 3 深度学习中的特征提取与选择...
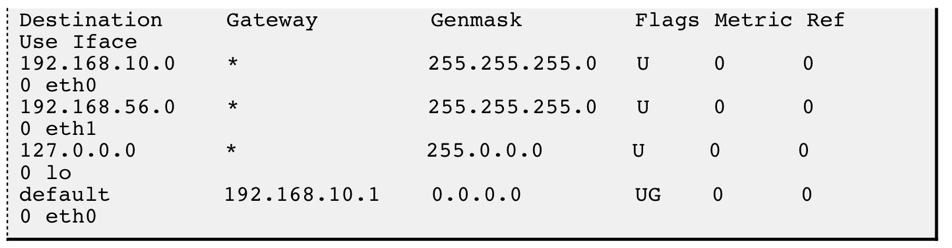
【Linux 网络】网络层协议之IP协议
IP协议 IP协议所处的位置网络层要解决的问题IP协议格式分片与组装网段划分特殊的IP地址IP地址的数量限制私网IP地址和公网IP地址路由 IP协议所处的位置 IP指网际互连协议,Internet Protocol的缩写,是TCP/IP体系中的网络层协议。 网络层要解决的问题 网络…...

.meta 文件
.meta 文件的作用简单来说是建立 Unity 与资源之间的“桥梁”。 在游戏中引用一个游戏资源,Unity 并不是直接按照文件的路径或者名称,而是使用一个独一无二的 GUID 来指向工程里该资源文件。 这个 GUID 就是存储在 Unity 工程为每一个资源和文件…...
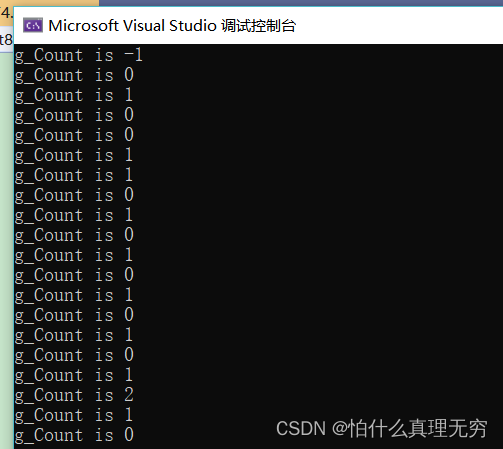
CRITICAL_SECTION 用法
#include <stdio.h> #include <windows.h> typedef RTL_CRITICAL_SECTION CRITICAL_SECTION; CRITICAL_SECTION g_cs; //声明关键段 // 共享资源 char g_cArray[10]; unsigned int g_Count 0; DWORD WINAPI ThreadProc10(LPVOID pParam) { // 进入临界区 …...
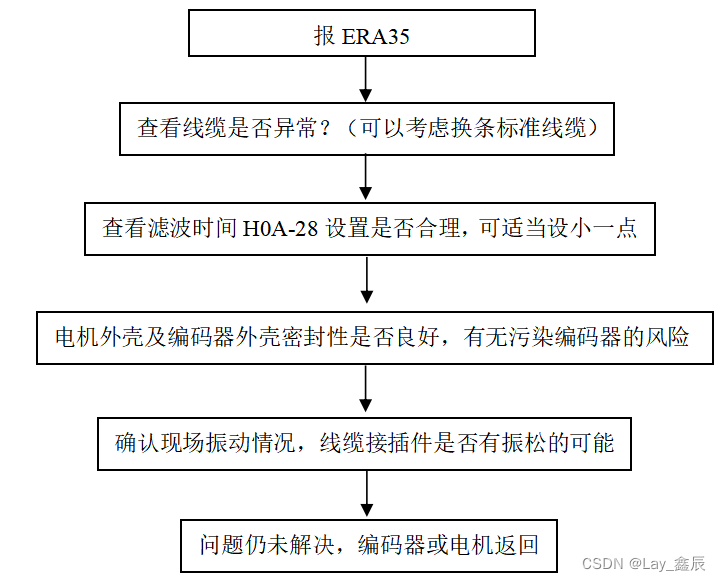
汇川运动控制产品故障排查
针对汇川伺服产品(IS600/IS620)的基本检测和一些出现频率较高的故障进行检测判断方法,适用于服务人员在现场排查/判断机器故障时,准确定位问题。 一、简单故障排查 注1:接线错误:1、UVW相序是否正确&#…...
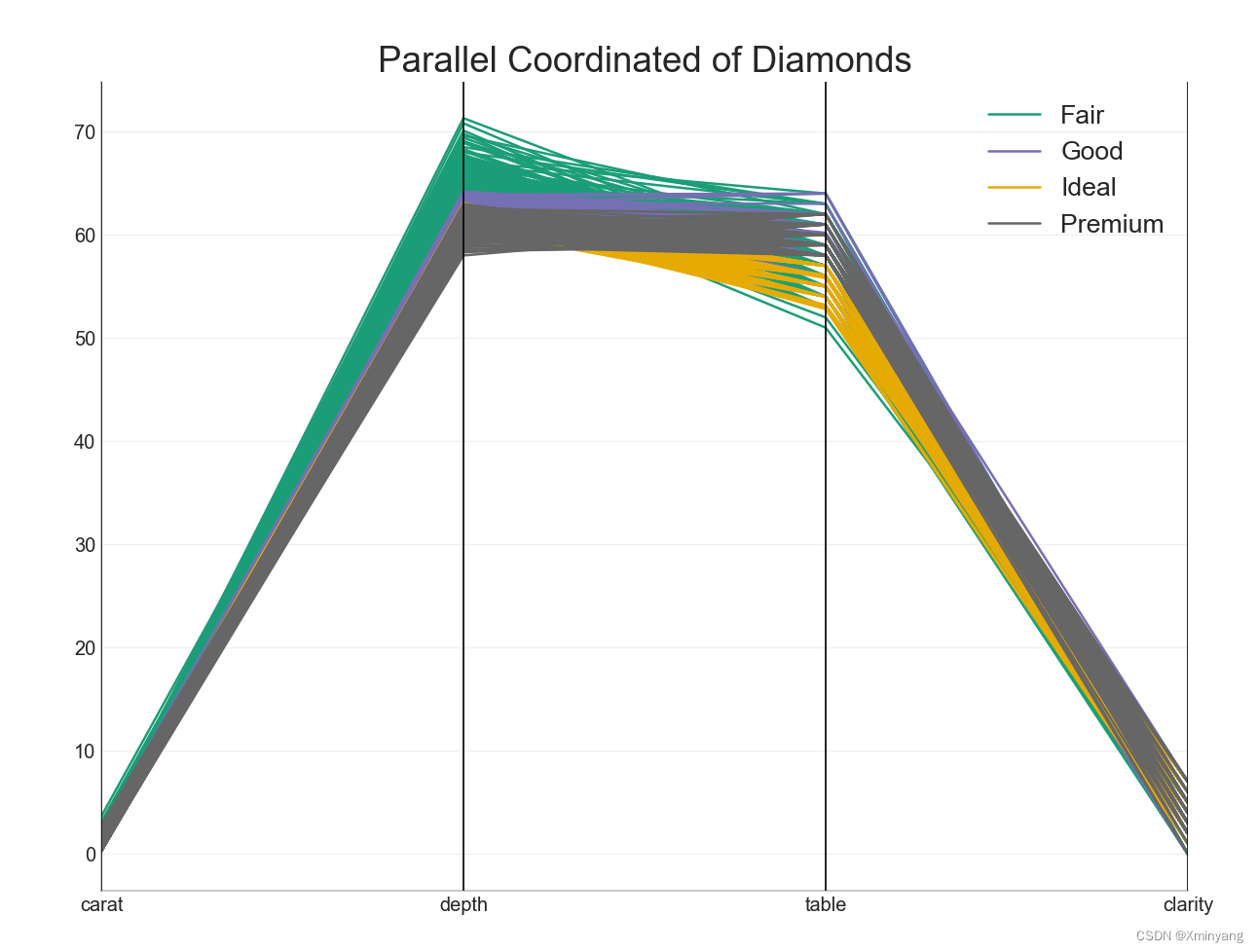
【Groups】50 Matplotlib Visualizations, Python实现,源码可复现
详情请参考博客: Top 50 matplotlib Visualizations 因编译更新问题,本文将稍作更改,以便能够顺利运行。 1 Dendrogram 树状图根据给定的距离度量将相似的点组合在一起,并根据点的相似性将它们组织成树状的链接。 新建文件Dendrogram.py: …...
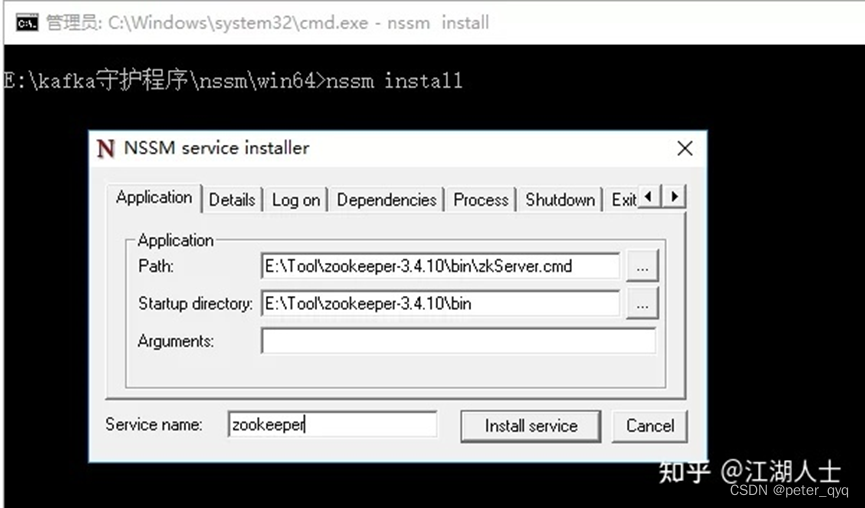
windows安装kafka配置SASL-PLAIN安全认证
目录 1.Windows安装zookeeper: 1.1下载zookeeper 1.2 解压之后如图二 1.3创建日志文件 1.4复制 “zoo_sample.cfg” 文件 1.5更改 “zoo.cfg” 配置 1.6新建zk_server_jaas.conf 1.7修改zkEnv.cmd 1.8导入相关jar 1.9以上配置就配好啦,接下来启…...
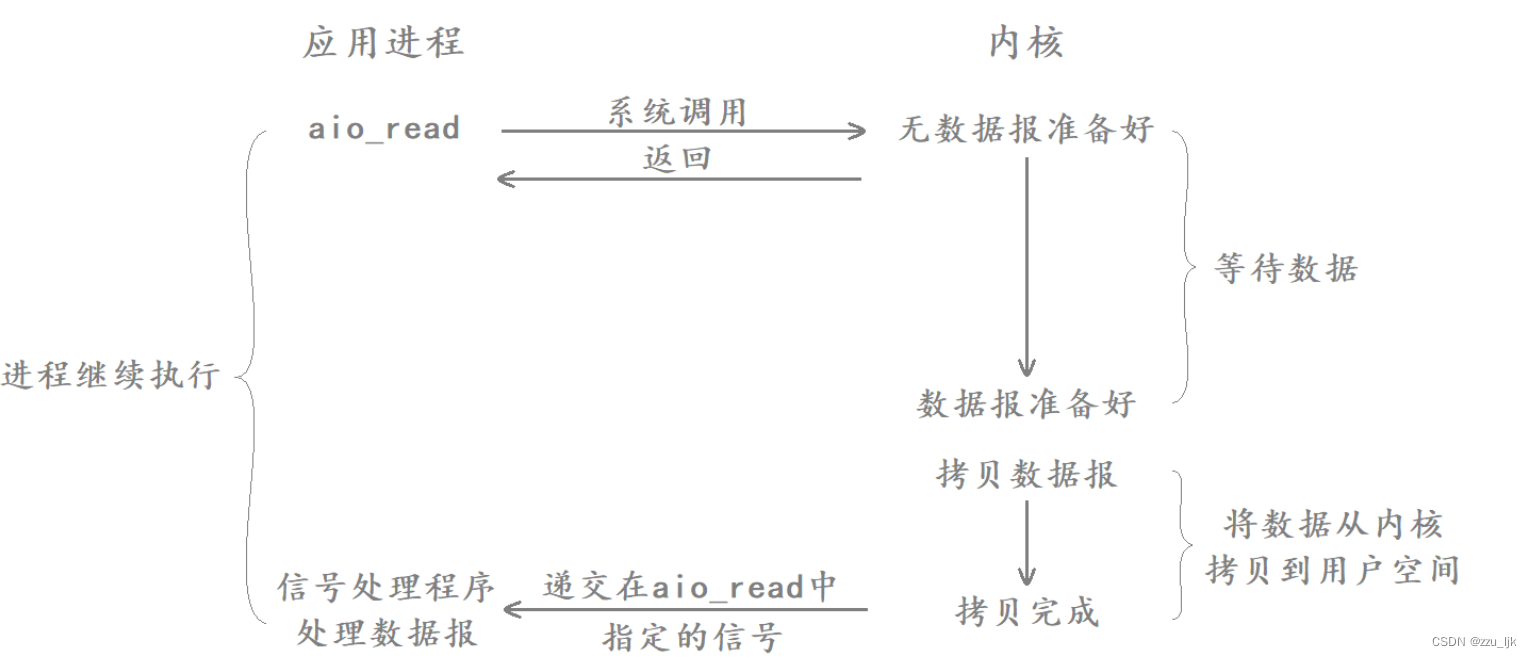
【Linux】五种IO模型
文章目录 1. IO基本概念2. 五种IO模型2.1 五个钓鱼的例子2.2 五种IO模型2.2.1 阻塞IO2.2.2 非阻塞IO2.2.3 信号驱动IO2.2.4 IO多路转接2.2.5 异步IO 1. IO基本概念 认识IO IO就是输入和输出,在冯诺依曼体系结构中,将数据从输入设备拷贝到内存就叫输入&am…...

SCT82A30DHKR_5.5V-100V Vin同步降压控制器
SCT82A30是一款100V电压模式控制同步降压控制器,具有线路前馈。40ns受控高压侧MOSFET的最小导通时间支持高转换比,实现从48V输入到低压轨的直接降压转换,降低了系统复杂性和解决方案成本。如果需要,在低至6V的输入电压下降期间&am…...

备忘录模式(C++)
定义 在不破坏封装性的前提下,捕获一-个对象的内部状态,并在该对象之外保存这个状态。这样以后就可以将该对象恢复到原先保存的状态。 应用场景 ➢在软件构建过程中,某些对象的状态在转换过程中,可能由于某种需要,要…...
)
二叉排序树(二叉查找树)
二叉排序树(二叉查找树)的性质: 若它的左子树不为空,则左子树上所有结点的值均小于它的根结点的值。若它的右子树不为空,则右子树上所有结点的值均大于它的根将诶点的值。它的左、右子树也分别为二叉排序树。 对二叉…...

Python简单应用VII
题目 编程实现下述各题。 1.使用异常处理结构捕获多种可能的异常,如列表下标索引越界异常(IndexError)、试 图访问一个系统对象没有的属性所发生的异常(AttributeError)、读一个文件但该文件不存在。 2. 新建并打开文件stud1.txt,如果文件已存在就提示“…...
mysql--InnoDB存储引擎--架构和事务
MySQL进阶篇 文章目录 架构1、逻辑结构InnoDB 逻辑存储单元主层级关系图:1、表空间2、段3、区4、页5、行总结: 2、架构2、1 内存架构2、2 磁盘架构 3、事务3、1事务基础(1)事务(2)特性 架构 1、逻辑结构 I…...
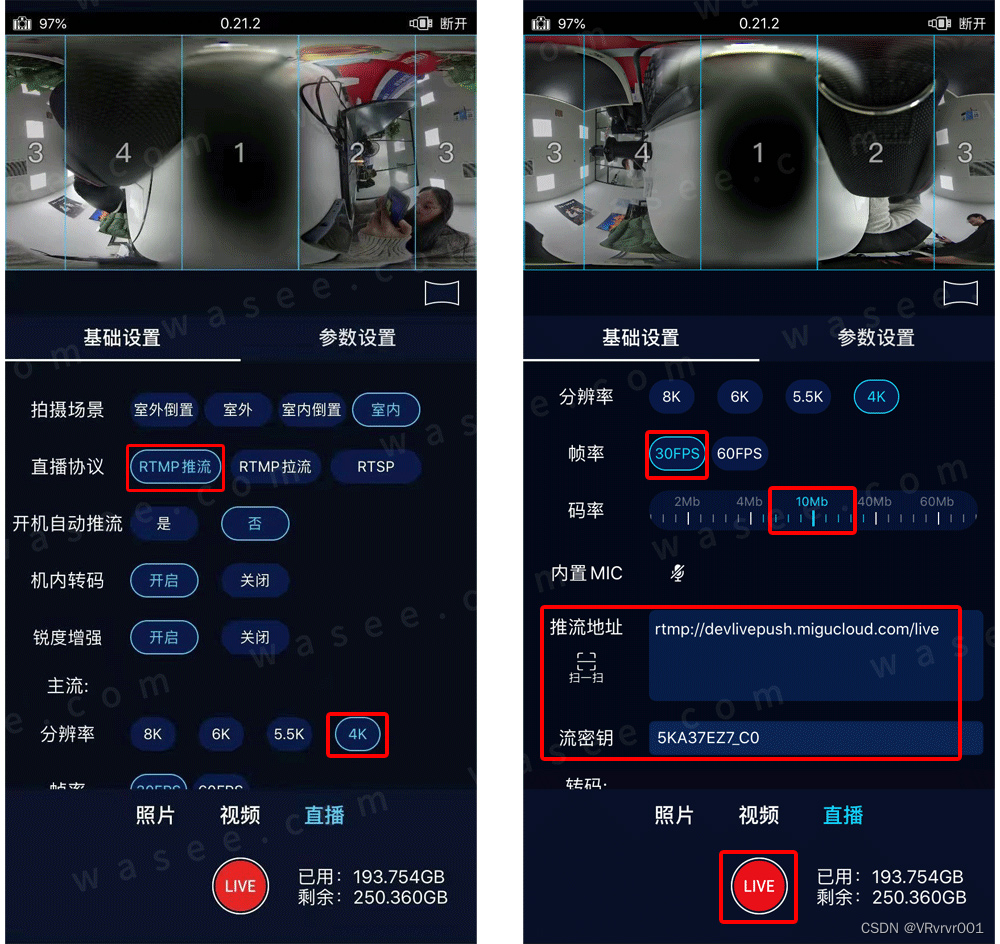
0基础学习VR全景平台篇 第79篇:全景相机-泰科易如何直播推流
泰科易科技是中国的一家研发全景相机的高科技公司,前不久,在2020世界VR产业大会上发布了新一代5G VR直播影像采集终端--360starlight。以其出色的夜景成像效果和一“部”到位的直播方案重新定义了VR慢直播相机,对行业具有高度借鉴意义。 本文…...

代码调试4:实现退化模型的训练
代码调试:实现退化模型的训练 作者:安静到无声 个人主页 目录 代码调试:实现退化模型的训练问题1:如何在coco原始编码的基础上修改原始的文件?**方法1**:修改生成的文件**方法2**:直接修改源文件`instances_train2014.json`和`instances_val2014.json`问题2:构建退化后…...
8.7工作总结
一、我们想自定义一个titileBar出现如下这种情况,发现他原来的titileBar还未隐藏。 后来我尝试修改主题使得他没有主题noActionBar发现也不行,后来我参考原先我看过的项目使用了如下代码 this.getActionBar().hide();发现会报这个错误java.lang.NullPoi…...

数据库的约束 详解
一、约束的概述 1.概念:约束是作用于表中字段上的规则,用于限制存储在表中的数据。 2.目的:保证数据库中数据的正确、有效性和完整性。 3.分类: 约束描述关键字非空约束限制该字段的数据不能为nullNOT NULL唯一约束保证该字段的所有数据都是唯一、不…...

Tomcat 编程式启动 JMX 监控
通过这篇文章,我们可以了解到,利用 JMX 技术可以方便获取 Tomcat 监控情况。但是我们采用自研的框架而非大家常见的 SpringBoot,于是就不能方便地通过设置配置开启 Tomcat 的 JMX,——尽管我们也是基于 Tomcat 的 Web 容器&#x…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

MFC 抛体运动模拟:常见问题解决与界面美化
在 MFC 中开发抛体运动模拟程序时,我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点,详细解析原因并提供解决方案,同时兼顾界面美化,让模拟效果更专业、更高效。 问题一:历史轨迹与小球残影残留 现象 小球运动后,历史位置的 “残影”…...

scikit-learn机器学习
# 同时添加如下代码, 这样每次环境(kernel)启动的时候只要运行下方代码即可: # Also add the following code, # so that every time the environment (kernel) starts, # just run the following code: import sys sys.path.append(/home/aistudio/external-libraries)机…...

群晖NAS如何在虚拟机创建飞牛NAS
套件中心下载安装Virtual Machine Manager 创建虚拟机 配置虚拟机 飞牛官网下载 https://iso.liveupdate.fnnas.com/x86_64/trim/fnos-0.9.2-863.iso 群晖NAS如何在虚拟机创建飞牛NAS - 个人信息分享...

华为OD机试-最短木板长度-二分法(A卷,100分)
此题是一个最大化最小值的典型例题, 因为搜索范围是有界的,上界最大木板长度补充的全部木料长度,下界最小木板长度; 即left0,right10^6; 我们可以设置一个候选值x(mid),将木板的长度全部都补充到x,如果成功…...

【SpringBoot自动化部署】
SpringBoot自动化部署方法 使用Jenkins进行持续集成与部署 Jenkins是最常用的自动化部署工具之一,能够实现代码拉取、构建、测试和部署的全流程自动化。 配置Jenkins任务时,需要添加Git仓库地址和凭证,设置构建触发器(如GitHub…...

学习一下用鸿蒙DevEco Studio HarmonyOS5实现百度地图
在鸿蒙(HarmonyOS5)中集成百度地图,可以通过以下步骤和技术方案实现。结合鸿蒙的分布式能力和百度地图的API,可以构建跨设备的定位、导航和地图展示功能。 1. 鸿蒙环境准备 开发工具:下载安装 De…...

云原生周刊:k0s 成为 CNCF 沙箱项目
开源项目推荐 HAMi HAMi(原名 k8s‑vGPU‑scheduler)是一款 CNCF Sandbox 级别的开源 K8s 中间件,通过虚拟化 GPU/NPU 等异构设备并支持内存、计算核心时间片隔离及共享调度,为容器提供统一接口,实现细粒度资源配额…...
