机器学习笔记之优化算法(九)收敛速度的简单认识
机器学习笔记之优化算法——收敛速度的简单认识
- 引言
- 收敛速度的判别标准
- R \mathcal R R-收敛速度
- 关于算法复杂度与收敛速度
引言
本节对收敛速度简单介绍。
收敛速度的判别标准
我们之前几节介绍了线搜索方法 ( Line Search Method ) (\text{Line Search Method}) (Line Search Method),并从方向角度、步长角度描述了先搜索方法的迭代优化过程。关于针对目标函数 f ( X ) f(\mathcal X) f(X)优化的终极目标: min X ∈ R n f ( X ) \mathop{\min}\limits_{\mathcal X \in \mathbb R^n} f(\mathcal X) X∈Rnminf(X),我们希望通过一系列数值解 { x k } k = 0 ∞ \{x_k\}_{k=0}^{\infty} {xk}k=0∞,使其对应的目标函数结果 { f ( x k ) } k = 0 ∞ \{f(x_k)\}_{k=0}^{\infty} {f(xk)}k=0∞收敛到最优值 f ∗ f^* f∗:
也可以等价写作: { x k } k = 0 ∞ ⇒ x ∗ ; f ( x ∗ ) = f ∗ \{x_k\}_{k=0}^{\infty} \Rightarrow x^*;f(x^*) = f^* {xk}k=0∞⇒x∗;f(x∗)=f∗。其中 x ∗ x^* x∗则表示迭代产生的最优数值解: x ∗ = arg min X ∈ R n f ( X ) x^* = \mathop{\arg\min}\limits_{\mathcal X \in \mathbb R^n} f(\mathcal X) x∗=X∈Rnargminf(X)
{ f ( x k ) } k = 0 ∞ ⇒ f ∗ \{f(x_k)\}_{k=0}^{\infty} \Rightarrow f^* {f(xk)}k=0∞⇒f∗
本节将介绍两种关于收敛速度的判别标准: Q \mathcal Q Q-收敛速度与 R \mathcal R R-收敛速度。
Q \mathcal Q Q-收敛速度
其中 Q \mathcal Q Q-收敛速度中的 Q \mathcal Q Q是指: Quotient \text{Quotient} Quotient,也就是除法中的商。该方式主要围绕迭代过程中数值解 x k , x k + 1 x_k,x_{k+1} xk,xk+1与最优解 x ∗ x^* x∗之间差异性的商值对收敛速度进行描述:
由于x k , x k + 1 , x ∗ x_k,x_{k+1},x^* xk,xk+1,x∗可能是∈ R n \in \mathbb R^n ∈Rn的向量,因此关于差异性的描述使用范数进行表示。而这个范数也可以理解为:数值解与最优解之间的距离,是一个正值。
lim k ⇒ ∞ ∣ ∣ x k + 1 − x ∗ ∣ ∣ ∣ ∣ x k − x ∗ ∣ ∣ \mathop{\lim}\limits_{k \Rightarrow \infty} \frac{||x_{k+1} - x^*||}{||x_k - x^*||} k⇒∞lim∣∣xk−x∗∣∣∣∣xk+1−x∗∣∣
在判断是否为 Q \mathcal Q Q-收敛时,我们事先假定:
- k k k充分大——这意味着 x k , x k + 1 x_k,x_{k+1} xk,xk+1都经过充分迭代产生的数值解,因而它们均无限趋近于 x ∗ x^* x∗。也就是说:无论 ∣ ∣ x k + 1 − x ∗ ∣ ∣ ||x_{k+1} - x^*|| ∣∣xk+1−x∗∣∣还是 ∣ ∣ x k − x ∗ ∣ ∣ ||x_{k} - x^*|| ∣∣xk−x∗∣∣,它们都可视作无穷小量:
{ lim k ⇒ ∞ ∣ ∣ x k + 1 − x ∗ ∣ ∣ = 0 lim k ⇒ ∞ ∣ ∣ x k − x ∗ ∣ ∣ = 0 \begin{cases} \mathop{\lim}\limits_{k \Rightarrow \infty} ||x_{k+1} - x^*|| = 0 \\ \mathop{\lim}\limits_{k \Rightarrow \infty} ||x_{k} - x^*|| = 0 \\ \end{cases} ⎩ ⎨ ⎧k⇒∞lim∣∣xk+1−x∗∣∣=0k⇒∞lim∣∣xk−x∗∣∣=0 - x k x_k xk与 f ( x k ) f(x_k) f(xk)同理——这个意思并不是说 x k x_k xk与 f ( x k ) f(x_k) f(xk)可以进行相互替换,而是说在 Q \mathcal Q Q-收敛中, f ( x k ) f(x_k) f(xk)与· x k x_k xk一样存在相同形式的定义:
这两个定义在Q \mathcal Q Q-收敛中没有区别,针对具体情况都可以进行使用。
lim k ⇒ ∞ ∣ ∣ f ( x k + 1 ) − f ∗ ∣ ∣ ∣ ∣ f ( x k ) − f ∗ ∣ ∣ \mathop{\lim}\limits_{k \Rightarrow \infty} \frac{|| f(x_{k+1}) - f^*||}{||f(x_k) - f^*||} k⇒∞lim∣∣f(xk)−f∗∣∣∣∣f(xk+1)−f∗∣∣
我们根据收敛速度的强度由低到高介绍 4 4 4种 Q \mathcal Q Q-收敛:
-
Q \mathcal Q Q-次线性收敛 ( Q-SubLinear Convergence ) (\text{Q-SubLinear Convergence}) (Q-SubLinear Convergence),其定义用数学符号表示为:
lim k ⇒ ∞ ∣ ∣ x k + 1 − x ∗ ∣ ∣ ∣ ∣ x k − x ∗ ∣ ∣ = 1 \mathop{\lim}\limits_{k \Rightarrow \infty} \frac{||x_{k+1} - x^*||}{||x_k - x^*||} = 1 k⇒∞lim∣∣xk−x∗∣∣∣∣xk+1−x∗∣∣=1 -
Q \mathcal Q Q-线性收敛 ( Q-Linear Convergence ) (\text{Q-Linear Convergence}) (Q-Linear Convergence)。对应数学符号表示为:
∣ ∣ x k + 1 − x ∗ ∣ ∣ ∣ ∣ x k − x ∗ ∣ ∣ ≤ a ∈ ( 0 , 1 ) \frac{||x_{k+1} - x^*||}{||x_k - x^*||} \leq a \in (0,1) ∣∣xk−x∗∣∣∣∣xk+1−x∗∣∣≤a∈(0,1)
我们发现,与 Q \mathcal Q Q-次线性收敛不同的是,它并没有加极限符号。并且:差异性的比值被 ( 0 , 1 ) (0,1) (0,1)范围内的常数 a a a限制着。例如:目标函数值集合 { f ( x k ) } k = 0 ∞ \{f(x_k)\}_{k=0}^{\infty} {f(xk)}k=0∞服从函数 G ( k ) = 2 − k \mathcal G(k) = 2^{-k} G(k)=2−k。其定义域内对应的函数图像表示如下:

可以发现:随着 k ⇒ ∞ k \Rightarrow \infty k⇒∞,可以得到最优解 f ∗ = 0 f^* = 0 f∗=0,而对应的 ∣ ∣ f ( x k + 1 ) − f ∗ ∣ ∣ ∣ ∣ f ( x k ) − f ∗ ∣ ∣ \begin{aligned}\frac{||f(x_{k+1}) - f^*||}{||f(x_k) - f^*||}\end{aligned} ∣∣f(xk)−f∗∣∣∣∣f(xk+1)−f∗∣∣在图像中可表示为相邻红色直线之间的比值。这个比值的计算结果为:
∣ ∣ f ( x k + 1 ) − f ∗ ∣ ∣ ∣ ∣ f ( x k ) − f ∗ ∣ ∣ = 2 − ( k + 1 ) − 0 2 − k − 0 = 1 2 \frac{||f(x_{k+1}) - f^*||}{||f(x_k) - f^*||} = \frac{2^{-(k+1)} - 0}{2^{-k} - 0} = \frac{1}{2} ∣∣f(xk)−f∗∣∣∣∣f(xk+1)−f∗∣∣=2−k−02−(k+1)−0=21
因此,由 G ( k ) \mathcal G(k) G(k)表示的 { f ( x k ) } k = 0 ∞ \{f(x_k)\}_{k=0}^{\infty} {f(xk)}k=0∞是 a = 1 2 \begin{aligned}a = \frac{1}{2}\end{aligned} a=21的 Q \mathcal Q Q-线性收敛。
此处所谓线性是指:将 { f ( x k ) } k = 0 ∞ \{f(x_k)\}_{k=0}^{\infty} {f(xk)}k=0∞视作为误差序列。也就是说:随着迭代次数 k k k的增加,误差信息 G ( k ) \mathcal G(k) G(k)越来越小,最终减少到 0 0 0。对误差取对数操作后,其结果 log G ( k ) \log \mathcal G(k) logG(k)与 k k k之间呈线性关系:
这里关于log \log log取底数为2 2 2。
log G ( k ) = log 2 2 − k = − k \log \mathcal G(k) = \log_2 2^{-k} =-k logG(k)=log22−k=−k
当 a a a取到极限 1 1 1时, Q \mathcal Q Q-线性收敛会退化至 Q \mathcal Q Q-次线性收敛;相反,当 a a a取到极限 0 0 0时, Q \mathcal Q Q-线性收敛会进化至 Q \mathcal Q Q-超线性收敛。反过来说:- 为什么被称作 Q \mathcal Q Q-次线性收敛是因为:相比 Q \mathcal Q Q-线性收敛中相邻迭代产生的差异性比值能够明显地用 a ∈ ( 0 , 1 ) a \in (0,1) a∈(0,1)描述出来;而 Q \mathcal Q Q-次线性收敛中相邻迭代产生的差异性几乎完全相同,它们之间的差距可以忽略不计。从而才有:
很明显,相比Q \mathcal Q Q-次线性收敛,Q \mathcal Q Q-线性收敛的差异性更明显,收敛的速度更快。
lim k ⇒ ∞ ∣ ∣ x k + 1 − x ∗ ∣ ∣ ∣ ∣ x k − x ∗ ∣ ∣ = 1 \mathop{\lim}\limits_{k \Rightarrow \infty} \frac{||x_{k+1} - x^*||}{||x_k - x^*||} = 1 k⇒∞lim∣∣xk−x∗∣∣∣∣xk+1−x∗∣∣=1
例如: G ( k ) = 1 k \begin{aligned}\mathcal G(k) = \frac{1}{k}\end{aligned} G(k)=k1就是一个明显的 Q \mathcal Q Q-次线性收敛。其对应函数图像表示如下:
很明显,相比上述的G ( k ) = 2 − k \mathcal G(k)=2^{-k} G(k)=2−k,随着迭代次数k k k的增加,相邻红色线比值的变化并不非常明显。

其次通过计算比值也能观察到类似的效果:
很明显,当充分迭代之后,此时k k k已经充分大,而k k + 1 \begin{aligned}\frac{k}{k+1}\end{aligned} k+1k这样的收敛效果完全可以忽略不计。
lim k ⇒ ∞ ∣ ∣ f ( x k + 1 ) − f ∗ ∣ ∣ ∣ ∣ f ( x k ) − f ∗ ∣ ∣ = lim k ⇒ ∞ 1 k + 1 − 0 1 k − 0 = lim k ⇒ ∞ k k + 1 = 1 \mathop{\lim}\limits_{k \Rightarrow \infty}\frac{||f(x_{k+1}) - f^*||}{||f(x_k) - f^*||} = \mathop{\lim}\limits_{k \Rightarrow \infty}\frac{\frac{1}{k+1} - 0}{\frac{1}{k} - 0} = \mathop{\lim}\limits_{k \Rightarrow \infty}\frac{k}{k+1} = 1 k⇒∞lim∣∣f(xk)−f∗∣∣∣∣f(xk+1)−f∗∣∣=k⇒∞limk1−0k+11−0=k⇒∞limk+1k=1
- 为什么被称作 Q \mathcal Q Q-次线性收敛是因为:相比 Q \mathcal Q Q-线性收敛中相邻迭代产生的差异性比值能够明显地用 a ∈ ( 0 , 1 ) a \in (0,1) a∈(0,1)描述出来;而 Q \mathcal Q Q-次线性收敛中相邻迭代产生的差异性几乎完全相同,它们之间的差距可以忽略不计。从而才有:
-
与 Q \mathcal Q Q-次线性收敛相反, Q \mathcal Q Q-超线性收敛 ( Q-Superlinear Convergence ) (\text{Q-Superlinear Convergence}) (Q-Superlinear Convergence)的定义用数学符号表示为:
这意味着相邻迭代次数之间差异性极大,使得x k + 1 x_{k+1} xk+1对应的差异性结果与x k x_k xk的差异性结果相比小到可以忽略不计,这里不再过多赘述。
lim k ⇒ ∞ ∣ ∣ x k + 1 − x ∗ ∣ ∣ ∣ ∣ x k − x ∗ ∣ ∣ = 0 \mathop{\lim}\limits_{k \Rightarrow \infty} \frac{||x_{k+1} - x^*||}{||x_k - x^*||} = 0 k⇒∞lim∣∣xk−x∗∣∣∣∣xk+1−x∗∣∣=0 -
Q \mathcal Q Q-二次收敛 ( Q-Quadratic Convergence ) (\text{Q-Quadratic Convergence}) (Q-Quadratic Convergence)的定义用数学符号表示为:
同理,如Q \mathcal Q Q-三次收敛 ( Cubic Convergence ) (\text{Cubic Convergence}) (Cubic Convergence)等等,仅与分母中的指数项相关。相比于线性收敛中a ∈ ( 0 , 1 ) a \in (0, 1) a∈(0,1),我们在Q \mathcal Q Q-二次收敛中不会更多计较a a a的范围,因为无穷小量的级别就可以说明其收敛速度。
∣ ∣ x k + 1 − x ∗ ∣ ∣ ∣ ∣ x k − x ∗ ∣ ∣ 2 ≤ a ∈ ( 0 , + ∞ ) \frac{||x_{k+1} - x^*||}{||x_k - x^*||^2} \leq a \in (0,+\infty) ∣∣xk−x∗∣∣2∣∣xk+1−x∗∣∣≤a∈(0,+∞)
与 Q \mathcal Q Q-线性收敛的定义类似,也同样没有极限符号。由于 ∣ ∣ x k − x ∗ ∣ ∣ ||x_k - x^*|| ∣∣xk−x∗∣∣自身就是一个无穷小量,那么它的平方结果可理解为一个更高级别的无穷小量,反过来说明:如果 x k + 1 x_{k+1} xk+1差异性所描述的无穷小量与 x k x_k xk差异性的平方所描述的无穷小量是一个级别的话,那么它的收敛速度已经超越了线性范畴。
例如: G ( k ) = 2 − 2 k \mathcal G(k) = 2^{-2^{k}} G(k)=2−2k就是明显的 Q \mathcal Q Q-二次收敛。其对应的函数图像表示如下:
很明显,相比上面的收敛,它的收敛速度更快了,这里不再过多赘述。

对应比值的计算结果是:
G ( k + 1 ) − 0 [ G ( k ) ] 2 = 2 − 2 k + 1 [ 2 − 2 k ] 2 = 1 ∈ ( 0 , + ∞ ) \begin{aligned}\frac{\mathcal G(k+1) -0}{[\mathcal G(k)]^2} = \frac{2^{-2^{k+1}}}{[2^{-2^k}]^2} = 1 \in (0, +\infty)\end{aligned} [G(k)]2G(k+1)−0=[2−2k]22−2k+1=1∈(0,+∞)
R \mathcal R R-收敛速度
其中 R \mathcal R R-收敛速度中的 R \mathcal R R是指: Root \text{Root} Root。关于假设条件与 Q \mathcal Q Q-收敛速度相同,这里不再赘述:
- k k k充分大;
- x k x_k xk与 f ( x k ) f(x_k) f(xk)共用相同概念。
关于 R \mathcal R R-收敛速度定义的数学符号表示如下:
∣ ∣ x k − x ∗ ∣ ∣ ≤ t k ||x_k - x^*|| \leq t_k ∣∣xk−x∗∣∣≤tk
其中 ∣ ∣ x k − x ∗ ∣ ∣ ||x_k - x^*|| ∣∣xk−x∗∣∣依然是数值解与最优解之间的差异性信息(距离范数);该结果被另外一个序列 { t k } k = 0 ∞ \{t_k\}_{k=0}^{\infty} {tk}k=0∞限制住:
- 如果 t k t_k tk是 Q \mathcal Q Q-次线性/线性/超线性/二次收敛;
- 并且 lim k ⇒ ∞ t k = 0 \mathop{\lim}\limits_{k \Rightarrow \infty} t_k = 0 k⇒∞limtk=0;
这说明{ t k } k = 0 ∞ \{t_k\}_{k=0}^{\infty} {tk}k=0∞是一个误差序列而不是数值解序列。上面的函数例子中,我们使用这些函数描述的是数值解序列 { x k } k = 0 ∞ \{x_k\}_{k=0}^{\infty} {xk}k=0∞或者 { f ( x k ) } k = 0 ∞ \{f(x_k)\}_{k=0}^{\infty} {f(xk)}k=0∞,但这里示例函数G ( k ) \mathcal G(k) G(k)最终都会收敛到0 0 0,因而也可以将其视作误差序列。
则称 x k x_k xk是 R \mathcal R R-次线性/线性/超线性/二次收敛。
可以看出: Q \mathcal Q Q与 R \mathcal R R的区别在于:
关于差异性的描述:Q ⇒ ∣ ∣ x k + 1 − x ∗ ∣ ∣ ∣ ∣ x k − x ∗ ∣ ∣ p ( p = 1 , 2 , 3 , ⋯ ) \begin{aligned}\mathcal Q \Rightarrow \frac{||x_{k+1} - x^*||}{||x_k - x^*||^p}(p=1,2,3,\cdots)\end{aligned} Q⇒∣∣xk−x∗∣∣p∣∣xk+1−x∗∣∣(p=1,2,3,⋯)与R ⇒ ∣ ∣ x k − x ∗ ∣ ∣ \mathcal R \Rightarrow ||x_k - x^*|| R⇒∣∣xk−x∗∣∣相比于Q \mathcal Q Q中使用具体值(0、1)或者范围 ( 0 , 1 ) ; ( 0 , + ∞ ) (0,1);(0,+\infty) (0,1);(0,+∞), R \mathcal R R则使用误差序列 { t k } k = 0 ∞ \{t_k\}_{k=0}^{\infty} {tk}k=0∞,并且每一个迭代步骤k = 0 , 1 , 2 , ⋯ k=0,1,2,\cdots k=0,1,2,⋯均被对应{ t k } k = 0 ∞ \{t_k\}_{k=0}^{\infty} {tk}k=0∞中的t 0 , t 1 , t 2 , ⋯ t_0,t_1,t_2,\cdots t0,t1,t2,⋯限制住。
之所以会定义 R \mathcal R R-收敛速度,原因在于:一些情况下, Q \mathcal Q Q-收敛速度不容易求解,如果找到一组合适的 { t k } k = 0 ∞ \{t_k\}_{k=0}^{\infty} {tk}k=0∞,可以根据 t k t_k tk的收敛速度,从而对 x k x_k xk的收敛速度进行表达。例如:
∣ ∣ f ( x k ) − f ∗ ∣ ∣ ≤ G ( k ) = 1 k ||f(x_k) - f^*|| \leq \mathcal G(k) = \frac{1}{k} ∣∣f(xk)−f∗∣∣≤G(k)=k1
我们已经知道:满足 G ( k ) \mathcal G(k) G(k)的误差序列是 Q \mathcal Q Q-次线性收敛,因而可以判断 { f ( x k ) } k = 0 ∞ \{f(x_k)\}_{k=0}^{\infty} {f(xk)}k=0∞是 R − \mathcal R- R−次线性收敛。
关于算法复杂度与收敛速度
在真实情况下,我们不能任由算法无限迭代下去,即 k k k不能无限大。因而我们会设置一些判断条件。例如:
这里 ϵ \epsilon ϵ表示描述限制条件的超参数。达到该条件,即可停止算法。
∣ ∣ f ( x k ) − f ∗ ∣ ∣ ≤ ϵ ||f(x_k) - f^*|| \leq \epsilon ∣∣f(xk)−f∗∣∣≤ϵ
- 如果依然以 Q \mathcal Q Q-次线性收敛 1 k \begin{aligned}\frac{1}{k}\end{aligned} k1为例,需要满足:
∣ ∣ f ( x k ) − f ∗ ∣ ∣ ≤ G ( k ) = 1 k ≤ ϵ ⇒ k ≥ 1 ϵ ||f(x_k) - f^*|| \leq \mathcal G(k) =\frac{1}{k} \leq \epsilon \Rightarrow k \geq \frac{1}{\epsilon} ∣∣f(xk)−f∗∣∣≤G(k)=k1≤ϵ⇒k≥ϵ1
可以看出:当 ϵ \epsilon ϵ越小时,迭代的次数 k k k越大。 - 如果以 Q \mathcal Q Q-线性收敛 2 − k 2^{-k} 2−k为例,需要满足:
2 − k ≤ ϵ ⇒ k ≥ log 2 1 ϵ 2^{-k} \leq \epsilon \Rightarrow k \geq \log_2 \frac{1}{\epsilon} 2−k≤ϵ⇒k≥log2ϵ1
可以观察到:在 ϵ \epsilon ϵ很小的情况下,关于 1 ϵ \begin{aligned}\frac{1}{\epsilon}\end{aligned} ϵ1其量级远高于 log 2 1 ϵ \begin{aligned}\log_2 \frac{1}{\epsilon}\end{aligned} log2ϵ1:
随着 1 ϵ \begin{aligned}\frac{1}{\epsilon}\end{aligned} ϵ1的增加, Q \mathcal Q Q-次线性收敛(蓝色直线)与 Q \mathcal Q Q-线性收敛(橙色曲线)对应的函数结果相比,其对应函数值的增速明显更高,而更高意味着更多的迭代步骤。

因此,一般情况下,使用更高强度的收敛速度,那么他的迭代步骤就会减小,从而降低算法复杂度。
相关参考:
【优化算法】收敛速度简介
优化里的Q-linear Convergence和R-linear convergence是什么意思?
相关文章:

机器学习笔记之优化算法(九)收敛速度的简单认识
机器学习笔记之优化算法——收敛速度的简单认识 引言收敛速度的判别标准 Q \mathcal Q Q-收敛速度 R \mathcal R R-收敛速度关于算法复杂度与收敛速度 引言 本节对收敛速度简单介绍。 收敛速度的判别标准 我们之前几节介绍了线搜索方法 ( Line Search Method ) (\text{Line …...
FPGA学习——Altera IP核调用之PLL篇
文章目录 一、IP核1.1 IP核简介1.2 FPGA中IP核的分类1.3 IP核的缺陷 二、PLL简介2.1 什么是PLL2.2 PLL结构图2.3 C4开发板上PLL的位置 三、IP核调用步骤四、编写测试代码五、总结 一、IP核 1.1 IP核简介 IP核(知识产权核),是在集成电路的可…...

经纬度坐标工具
LngLatUtil :用于计算里程数 import cn.hutool.core.util.ArrayUtil; import com.alibaba.fastjson.JSON; import com.alibaba.fastjson.JSONObject; import lombok.Getter; import lombok.Setter;import java.io.FileInputStream; import java.io.Serializable; import java.t…...

如何使用伪元素::before和::after?
伪元素(::before和::after)是CSS中非常有用的特性,它们允许你在元素的内容之前或之后插入额外的内容,并且不需要在HTML结构中添加额外的标记。这样可以方便地在页面上添加装饰性元素、图标、或者样式效果。以下是使用伪元素的基本方法: 1、创…...
Visual Studio Code中对打开的脚本格式统一
什么是Language Server Protocol (LSP)? Language Server Protocol(语言服务器协议,简称LSP)是微软在2016年提出的一套统一的通讯协议方案。LSP定义了一套编辑器或者IDE与语言服务器(Language Server)之间使用的协议&…...
补充JDK源码-IDEA集成工具
在阅读JDK8源码的时候发现,只有一小部分常用包是存在源码及其注释的,而很多内部包是没有源码,class文件在阅读的时候对阅读者十分不友好。在网上搜集了很多资料都没有解决问题。 解决问题办法:参考文档。本文主要是根据这篇文章记…...
Git Submodule 更新子库失败 fatal: Unable to fetch in submodule path
编辑本地目录 .git/config 文件 在 [submodule “Assets/CommonModule”] 项下 加入 fetch refs/heads/:refs/remotes/origin/...

Springboot切面打印日志
切面打印完整日志,以下代码用于扫描RestController 注解修饰的接口,并打印相关日志 import org.aspectj.lang.JoinPoint; import org.aspectj.lang.annotation.AfterReturning; import org.aspectj.lang.annotation.Aspect; import org.aspectj.lang.annotation.Before; impor…...
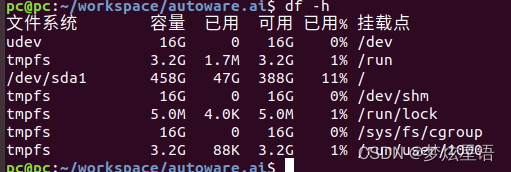
ubuntu上回环设备/dev/loop0占用100%清理
查看磁盘占用情况时: df -h/dev/loopn这些设备在Linux下被称为回环设备。 终端输入: sudo apt autoremove --purge snapd再次查看:...
List list=new ArrayList()抛出的ArrayIndexOutOfBoundsException异常
1.应用场景,今天生产日志监控到一下ArrayList 进行add 异常,具体日志如下: eptionHandler.handler(178): TXXYBUSSINESS|执行异常 java.util.concurrent.CompletionException: java.lang.ArrayIndexOutOfBoundsException: Index 1 out of bo…...

桶排序算法
桶排序算法 算法思想概述:桶排序的主要步骤如下: 算法goland实现:图解演示: 算法思想概述: 桶排序(Bucket Sort)是一种非比较性的排序算法,它将待排序的元素分到有限数量的桶&#…...

P8604 [蓝桥杯 2013 国 C] 危险系数
题目背景 抗日战争时期,冀中平原的地道战曾发挥重要作用。 题目描述 地道的多个站点间有通道连接,形成了庞大的网络。但也有隐患,当敌人发现了某个站点后,其它站点间可能因此会失去联系。 我们来定义一个危险系数 DF(x,y)&…...
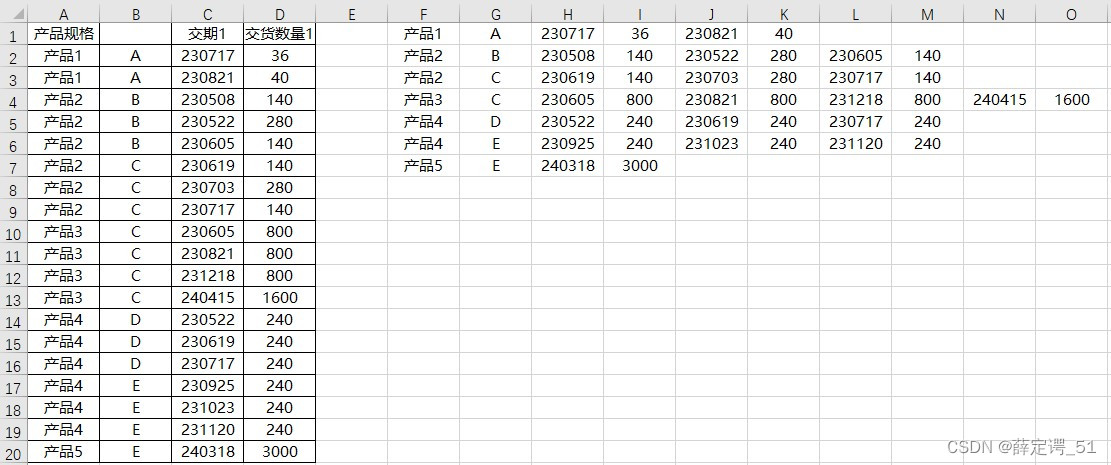
Excel·VBA表格横向、纵向相互转换
如图:对图中区域 A1:M6 横向表格,转换成区域 A1:C20 纵向表格,即 B:M 列转换成每2列一组按行写入,并删除空行。同理,反向操作就是纵向表格转换成横向表格 目录 横向转纵向实现方法1转换结果 实现方法2转换结果 纵向转横…...
Leetcode-每日一题【剑指 Offer 06. 从尾到头打印链表】
题目 输入一个链表的头节点,从尾到头反过来返回每个节点的值(用数组返回)。 示例 1: 输入:head [1,3,2]输出:[2,3,1] 限制: 0 < 链表长度 < 10000 解题思路 1.题目要求我们从尾到头反过…...

LeetCode--HOT100题(22)
目录 题目描述:160. 相交链表(简单)题目接口解题思路代码 PS: 题目描述:160. 相交链表(简单) 给你两个单链表的头节点 headA 和 headB ,请你找出并返回两个单链表相交的起始节点。如果两个链表…...
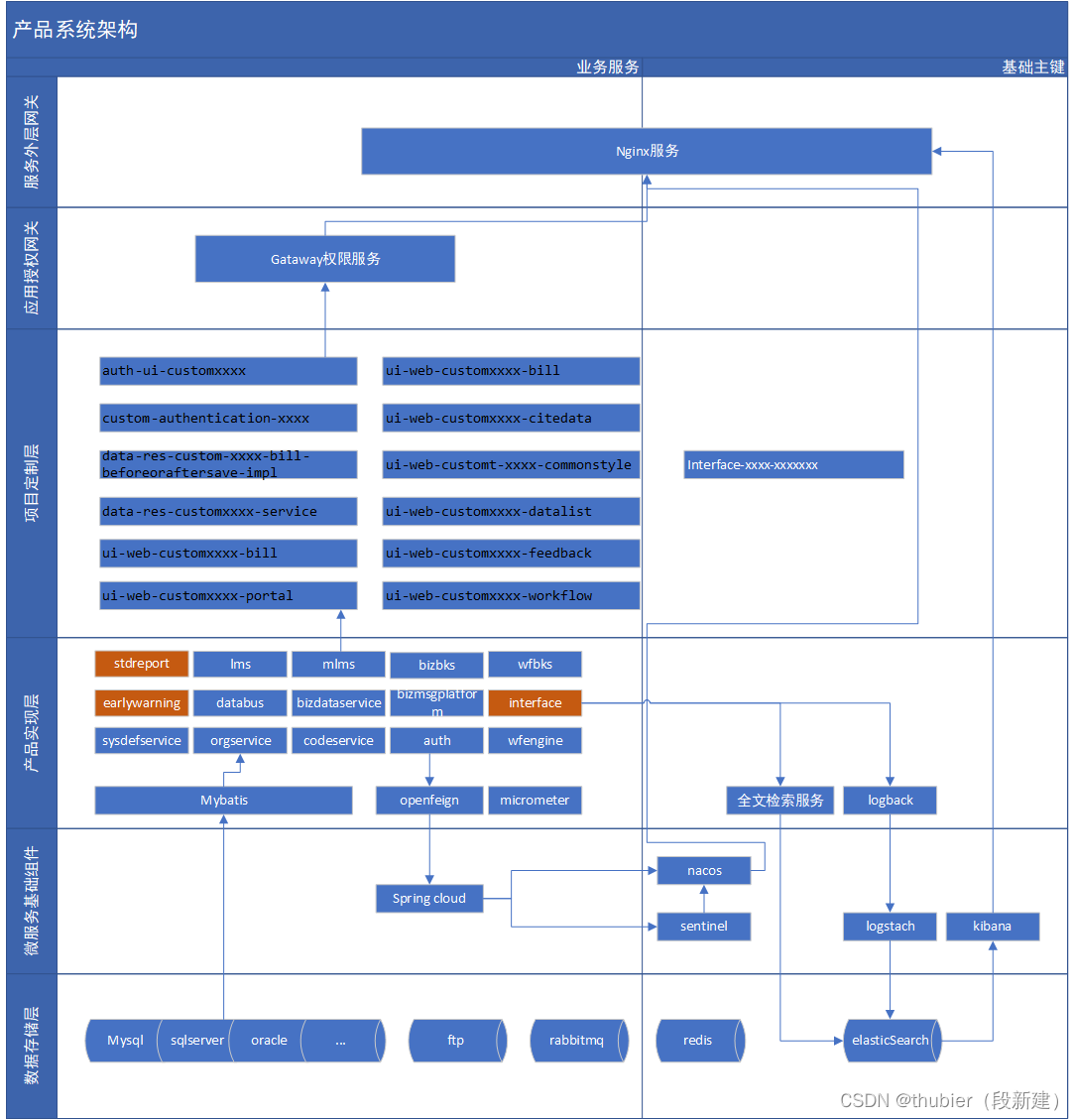
产品体系架构202308版
1.前言 当我们不断向前奔跑时,需要回头压实走过的路。不断扩张的同时把相应的内容沉淀下来,为后续的发展铺垫基石。 不知从何时起,产品的架构就面向了微服务/中台化/前后端分离/低代码化/分布式/智能化/运行可观测化的综合体,让…...

Linux systemctl 简单介绍与使用
在Linux下,systemctl是一个管理系统服务的命令。它提供了对systemd服务的控制和管理。 在系统中使用systemctl命令,您可以执行以下操作: 启动服务:systemctl start servicename停止服务:systemctl stop servicename重…...

恺英网络宣布:与华为鸿蒙系统展开合作,将开发多款手游
8月5日消息,恺英网络宣布旗下子公司盛和网络参加了华为开发者大会(HDC.Together)游戏服务论坛,并在华为鸿蒙生态游戏先锋合作启动仪式上进行了亮相。恺英网络表示,将逐步在HarmonyOS上开发多款游戏,利用Har…...

Vue CORS
使用Vue框架报错,客户端浏览器有CORS错误,怎么解决? 参考API Proxying During Development,可以新增或修改config/index.js下的proxyTable属性。 留意到 proxyTable的key值为/api,代表所有服务端域名都改成以/api开头…...
Godot 4 源码分析 - 文件读入编码处理
今天需要读入xml文件进行处理,结果读入一个带中文的文件时,出错了。当然程序还能运行,但编译器一直报错,而且XML解析也不正确 单步调试发现读入的内容出现乱码,具体逻辑: String FileAccess::get_as_text…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...

Webpack性能优化:构建速度与体积优化策略
一、构建速度优化 1、升级Webpack和Node.js 优化效果:Webpack 4比Webpack 3构建时间降低60%-98%。原因: V8引擎优化(for of替代forEach、Map/Set替代Object)。默认使用更快的md4哈希算法。AST直接从Loa…...

[ACTF2020 新生赛]Include 1(php://filter伪协议)
题目 做法 启动靶机,点进去 点进去 查看URL,有 ?fileflag.php说明存在文件包含,原理是php://filter 协议 当它与包含函数结合时,php://filter流会被当作php文件执行。 用php://filter加编码,能让PHP把文件内容…...
