rust实践-异步并发socket通信
客户端
[package]
name = "rust_client"
version = "0.1.0"
edition = "2021"[dependencies]
tokio = { version = "1.14.0", features = ["full"] }
use tokio::io::{self, AsyncReadExt, AsyncWriteExt};
use tokio::net::TcpStream;#[tokio::main]
async fn main() -> io::Result<()> {let mut stream = TcpStream::connect("127.0.0.1:7878").await?;let (mut rd, mut wr) = stream.split();let mut buf = vec![0; 1024];loop {let n = match rd.read(&am相关文章：
rust实践-异步并发socket通信
客户端 [package] name = "rust_client" version = "0.1.0" edition = "2021"[dependencies] tokio = {version = "1.14.0", features = ["full"] }use tokio::io::{self, AsyncReadExt, AsyncWriteExt}; use tokio::net::…...
SolidUI社区-根据Prompt打造人设
背景 随着文本生成图像的语言模型兴起，SolidUI想帮人们快速构建可视化工具，可视化内容包括2D,3D,3D场景，从而快速构三维数据演示场景。SolidUI 是一个创新的项目，旨在将自然语言处理（NLP）与计算机图形学相…...
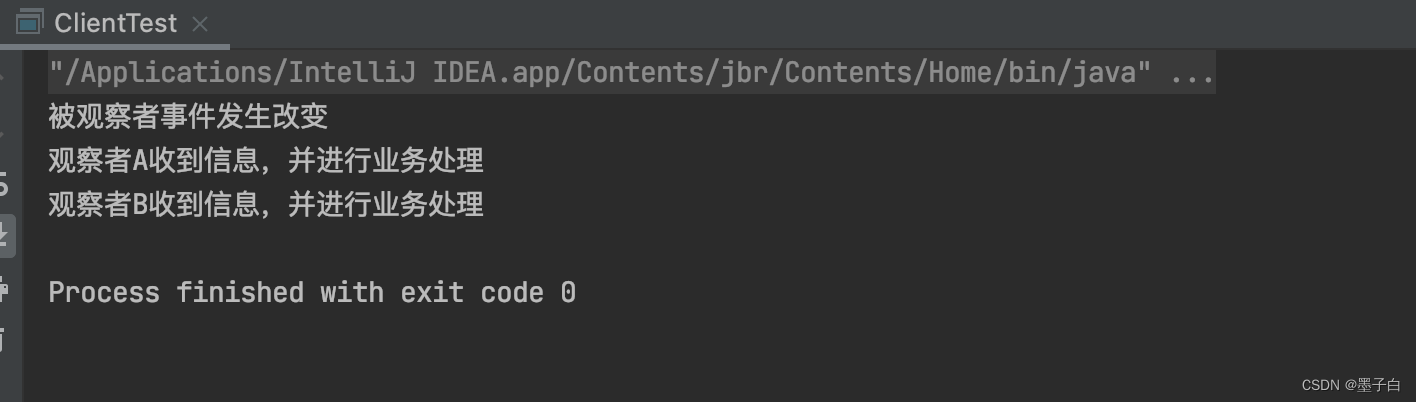
设计模式行为型——观察者模式
目录 什么是观察者模式 观察者模式的实现 观察者模式角色 观察者模式类图 观察者模式举例 观察者模式代码实现 观察者模式的特点 优点 缺点 使用场景 注意事项 实际应用 什么是观察者模式 观察者模式（Observer Pattern）是一种行为型设计模式…...
Kernel Exception导致手机重启案例分析
和你一起终身学习，这里是程序员Android 经典好文推荐，通过阅读本文，您将收获以下知识点: 一、高温触发 Kernel Exception 重启问题二、解决方案三、提高电池温度方案 一、 高温触发 Kernel Exception 重启问题 手机 电池温度 默认60度以上高温…...
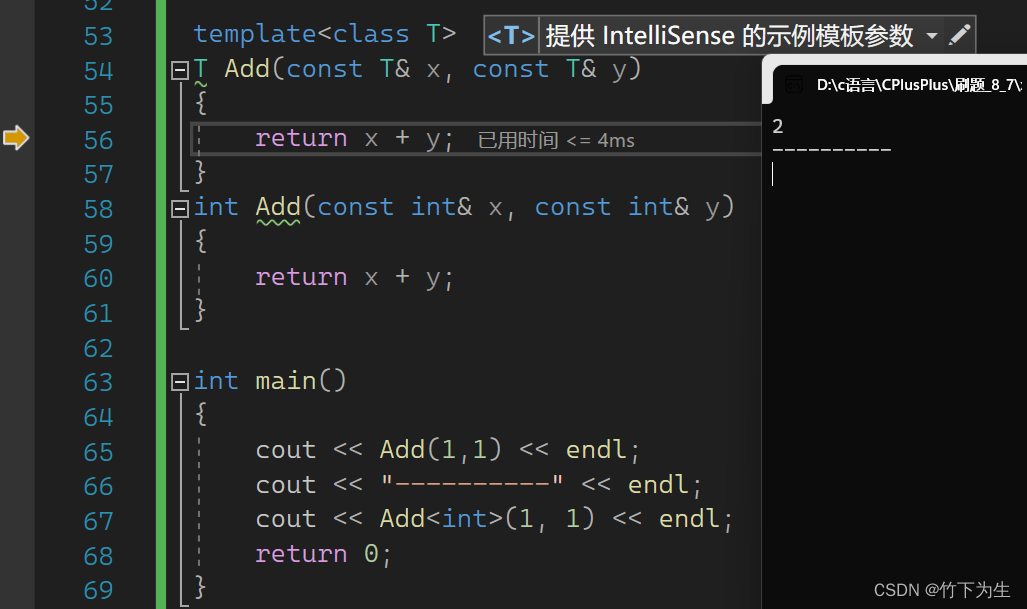
C++入门篇5---模板
相信大家都遇到过这么一种情况，为了满足不同类型的需求，我们要写多个功能相同，参数类型不同的代码，为此，C引入了泛型编程这一概念，而模板就是实现泛型编程的基础，其实本质就是我们写一个类似”模…...
L2CS-Net: 3D gaze estimation
L2CS-Net: Fine-Grained Gaze Estimation in Unconstrained Environments论文解析 摘要1. 简介2. Related Work3. METHOD3.1 Proposed loss function3.2 L2CS-Net 结构3.3 数据集3.4 评价指标 4. 实验4.1 实验结果 论文地址：L2CS-Net: Fine-Grained Gaze Estimation…...
kenernetes/k8s笔试面试
k8s的基础概念 k8s本质是一个容器编排系统，可以管理容器的生命周期，应用部署，更新，维护，应用提供服务，扩容缩容应用，故障自愈。 k8s与docker的关系 docker:是一种轻量级的虚拟化技术。运维层…...
我们真的是在做数据治理吗
我们真的是在做数据治理吗？ 什么是数据治理？ 数据治理和数据管理有什么区别？ 相信即使是考过数据治理工程师的人，面对这2个问题也仍然会有这个疑问。 目前国际和国内对于数据治理没有明确统一的定义，对于数据治理的服…...
聊聊汽车电子的话题
当谈到汽车电子时，有许多有趣的话题可以探讨。以下是一些可能感兴趣的话题： 自动驾驶技术：自动驾驶技术正变得越来越先进，它们如何在汽车中实现？它们将如何改变我们的交通方式以及对道路安全的影响？ 电动汽…...
ThinkPHP6企业OA办公系统
有需要请加文章底部Q哦 可远程调试 ThinkPHP6企业OA办公系统 一 介绍 勾股OA基于ThinkPHP6开发，前端Layui，数据库mysql，是一款实用的企业办公系统。可多角色登录，集成了系统设置、人事管理、消息管理、审批管理、日常办公、客户…...
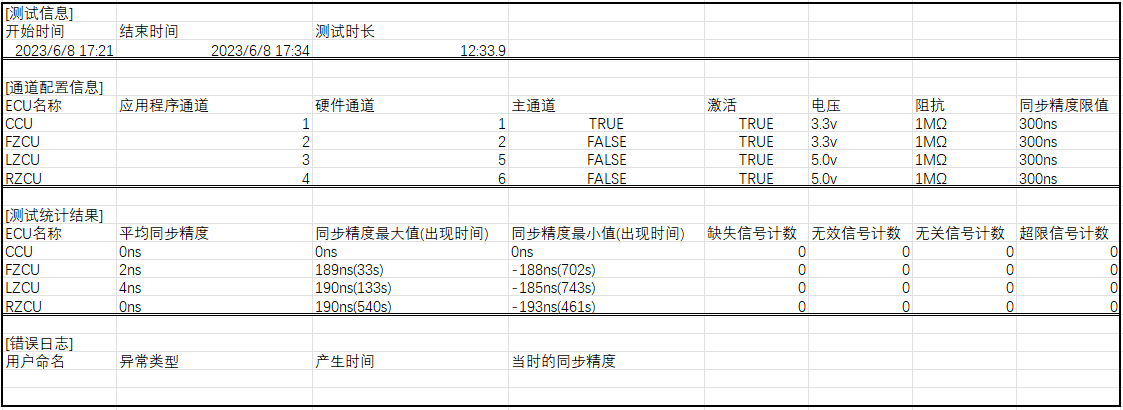
PPS Tester测量原理和实施方法
怿星科技发布了新品PPS Tester，这是一款基于1PPS方法的时间同步精度测试设备。PPS Tester由硬件模块ETS2110和上位机软件ePPSTester构成。本文将围绕此设备的应用场景，介绍相关概念和设备使用方法。 什么是时间同步？ 时间同步就是采取某项技…...
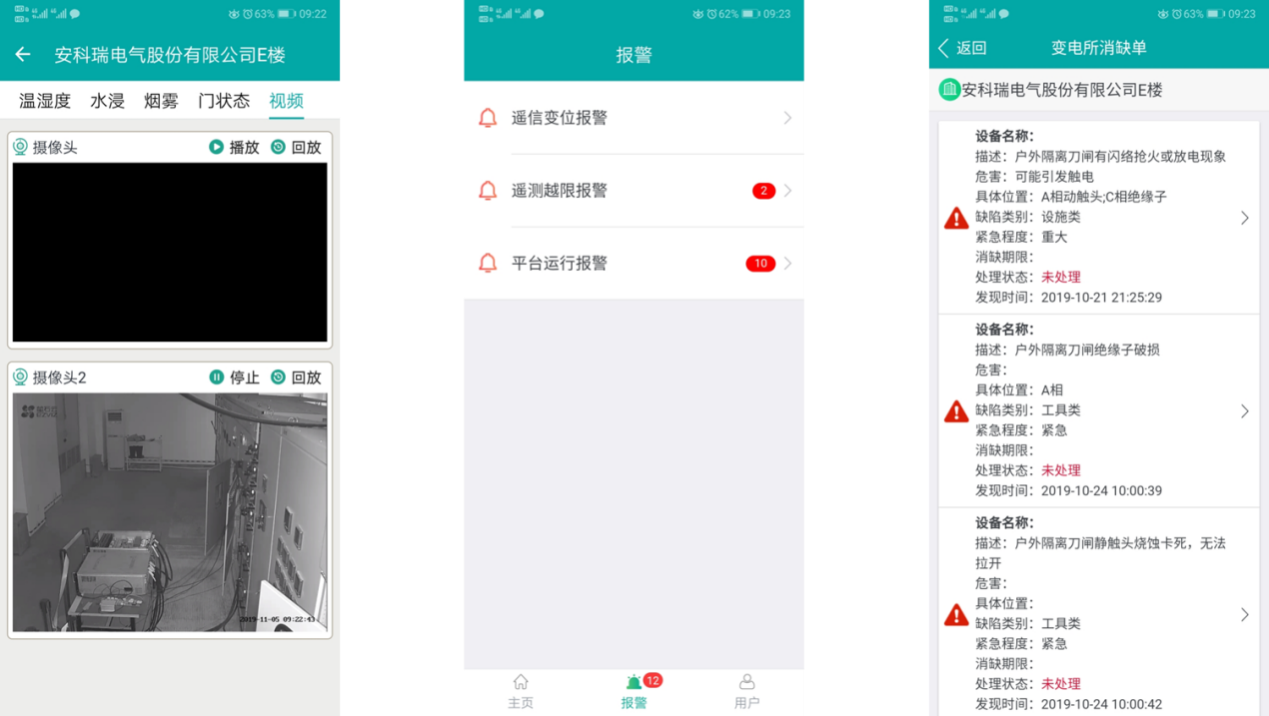
浅谈新电改背景下电网企业综合能源服务商业模式研究及发展方向
安科瑞 华楠 摘要: 新电改方案实施后，由于输配电价的改革和售电侧的放开，电网企业的盈利模式也随之发生了变化。这就要求电网企业转变服务理念与经营方式，来寻求竞争优势。基于“魏朱六要素商业模式”模型，对电网企业综合能源服务…...
SpringBoot + Docker 实现一次构建到处运行~
一、容器化部署的好处 图片 Docker 作为一种新兴的虚拟化方式，它可以更高效的利用系统资源，不需要进行硬件虚拟以及运行完整操作系统等额外开销。 传统的虚拟机技术启动应用服务往往需要数分钟，而 Docker 容器应用，由于直接运行…...
clang-format格式化代码
1. clang-format简介 Clang-Format可用于格式化（排版）多种不同语言的代码。其自带的排版格式主要有：LLVM, Google, Chromium, Mozilla, WebKit等; 利用style参数配置风格。通过编写 .clang-format 文件，可以实现代码风格的配置。…...
品牌宣传与媒体传播是声誉管理的主要方式之一
企业声誉是现如今影响品牌信任度、客户忠诚度的重要因素，也被视为企业的一种无形资，更影响着企业未来的发展。因此，企业声誉管理也日渐成为企业管理的重要课题之一，尤其在品牌营销管理领域。 什么是声誉管理？声誉管理有…...
2023年8月7日-8月13日，（上午熟悉公司代码，周一到周五晚上优先工作所急视频教程，其他业余时间进行ue视频教程，为独立游戏做准备）
按照规划，上午熟悉公司源码，下午进行filament和ue渲染，晚上写工作代码。回家后泛读pbrt或者其他书籍催眠。 业余学习ue的各种视频教程，为独立游戏做准备（公司也实行末位淘汰，给自己留条后路）。累…...
Vue3 第二节 Vue3的响应式
1.Vue3的响应式原理 2.ref函数和reactive函数的对比 3.setup注意点 一.Vue3的响应式原理 1.Vue2.x中的响应式原理 ① 实现原理 对象类型：通过Object.defineProperty() 对属性的读取，修改进行拦截（数据劫持）数组类型…...
通过easyui实现动态控制表格字段显示、导出表格数据
前言 学过layui前端框架的都知道，layui默认帮我们实现了控制表格字段显示以及数据的导出功能。 1、控制表格字段显示 2、数据导出 3、导出为pdf：导出按钮的右边那个按钮就是打印pdf的 那么，easyui要怎么实现这些功能呢？这篇文章就…...
JWT入门，jwt可以解密吗？
JWT 什么是 JWT JSON Web Token，通过数字签名的方式，以 JSON 对象为载体，在不同的服务终端之间安全地传输信息 官网：https://jwt.io/SDK: https://jwt.io/libraries (含Java和各种语言)Java SDK(上面的SDK链接得到): https://g…...
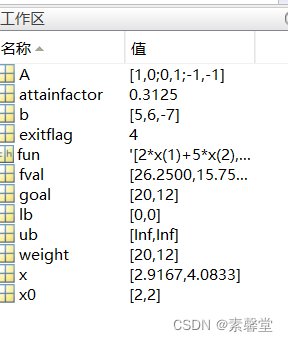
36.利用解fgoalattain 有约束多元变量多目标规划问题求解（matlab程序）
1.简述 多目标规划的一种求解方法是加权系数法，即为每一个目标赋值一个权系数，把多目标模型转化为一个单目标模型。MATLAB的fgoalattain()函数可以用于求解多目标规划。 基本语法 fgoalattain()函数的用法： x fgoalattain(fun,x0,goal,weig…...
Opencv中的addweighted函数
一.addweighted函数作用 addweighted（）是OpenCV库中用于图像处理的函数，主要功能是将两个输入图像（尺寸和类型相同）按照指定的权重进行加权叠加（图像融合），并添加一个标量值&#x…...
ETLCloud可能遇到的问题有哪些？常见坑位解析
数据集成平台ETLCloud，主要用于支持数据的抽取（Extract）、转换（Transform）和加载（Load）过程。提供了一个简洁直观的界面，以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...
k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN，根据VPN原理，打通两个内网必然需要借助一个公共中继节点，ktconnect工具巧妙的利用k8s原生的portforward能力，简化了建立连接的过程，apiserver间接起到了中继节…...
3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象，只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意：它移动的位置必须是相连的有内容的单元格…...
安卓基础（aar）
重新设置java21的环境，临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的： MyApp/ ├── app/ …...
LLMs 系列实操科普（1）
写在前面： 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容，原视频时长 ~130 分钟，以实操演示主流的一些 LLMs 的使用，由于涉及到实操，实际上并不适合以文字整理，但还是决定尽量整理一份笔…...
08. C#入门系列【类的基本概念】：开启编程世界的奇妙冒险
C#入门系列【类的基本概念】：开启编程世界的奇妙冒险 嘿，各位编程小白探险家！欢迎来到 C# 的奇幻大陆！今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类！别害怕，跟着我，保准让你轻松搞…...
【MATLAB代码】基于最大相关熵准则（MCC）的三维鲁棒卡尔曼滤波算法（MCC-KF），附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则（MCC）的三维鲁棒卡尔曼滤波算法（MCC-KF），针对传感器观测数据中存在的脉冲型异常噪声问题，通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现，验证了后者在状态估计鲁棒性方面的显著优…...
【FTP】ftp文件传输会丢包吗？批量几百个文件传输，有一些文件没有传输完整，如何解决？
FTP（File Transfer Protocol）本身是一个基于 TCP 的协议，理论上不会丢包。但 FTP 文件传输过程中仍可能出现文件不完整、丢失或损坏的情况，主要原因包括： ✅ 一、FTP传输可能“丢包”或文件不完整的原因 原因描述网络…...
链式法则中 复合函数的推导路径 多变量“信息传递路径”
非常好，我们将之前关于偏导数链式法则中不能“约掉”偏导符号的问题，统一使用 二重复合函数： z f ( u ( x , y ) , v ( x , y ) ) \boxed{z f(u(x,y),\ v(x,y))} zf(u(x,y), v(x,y)) 来全面说明。我们会展示其全微分形式（偏导…...