我在leetcode用动态规划炒股
事情是这样的,突然兴起的我在letcode刷题
- 121. 买卖股票的最佳时机
- 122. 买卖股票的最佳时机 II
- 123. 买卖股票的最佳时机 III
以上三题。
1. 121. 买卖股票的最佳时机

1.1. 暴力遍历,两次遍历
1.1.1. 算法代码
public class Solution {public int MaxProfit(int[] prices) {int profitValue=0;for(int i=0;i<prices.Length;i++){for(int j=i+1;j<prices.Length;j++){if(prices[j]>prices[i]){if(prices[j]-prices[i]>profitValue){profitValue=prices[j]-prices[i];}}}}return profitValue;}
}
上述代码的逻辑为两次遍历,后一个值比前一个值大,并使用哨兵变量profitValue记录最大差值。
1.1.2. 算法复杂度
- 时间复杂度: O ( n 2 ) = n ∗ ( n − 1 ) 2 O(n^2)=\frac {n*(n-1)}{2} O(n2)=2n∗(n−1)
- 空间复杂度: O ( 1 ) O(1) O(1),因为只有哨兵变量
profitValue
1.1.3. 算法问题
前面我们讲到,这个时间复杂度是 O ( n 2 ) O(n^2) O(n2),是一个指数函数。
那么在数据非常大的时候,其根据时间复杂度可以知道,其复杂度非常的高,如leetcode的超时案例
[886,729,539,474,5,653,588,198,313,111,38,808,848,364,819,747,520,568,583,253,605,442,779,903,217,284,927,33,859,75,418,612,174,316,167,40,945,740,174,279,985,133,38,919,528,844,101,291,673,561,.......
中间有3万个数值
.......561,644,484,868,53,936,186,35,219,84,455,971,922,862,434,553,948,857,491,622,162,934,66,486,569,690,596,506,452,635,690]
其时间复杂度是: 30000 ∗ 29999 / 2 = 449985000 30000*29999/2=449985000 30000∗29999/2=449985000,其计算数值大的可怕。
1.2. 一次遍历
1.2.1. 算法代码
public class Solution {public int MaxProfit(int[] prices) {int minprice = int.MaxValue;int maxprofit = 0;for (int i = 0; i < prices.Length; i++) {if (prices[i] < minprice) {minprice = prices[i];} else if (prices[i] - minprice > maxprofit) {maxprofit = prices[i] - minprice;}}return maxprofit;}
}
其算法,基本思路是:在最低点购入,在最高点卖出,由于for循环是从0开始的,所以其每一次minprice是当前时点前最低点购入值,故此算法可靠
1.2.2. 算法复杂度
- 时间复杂度: O ( n ) O(n) O(n)
- 空间复杂度: O ( 1 ) = 2 O(1)=2 O(1)=2
2.2 122. 买卖股票的最佳时机 II

第一题相较比较简单,而第二题中增加了一个限定:可以购买多次,只是手上最多只有一支股票
2.1. 贪心算法
2.1.1. 算法代码
public class Solution {public int MaxProfit(int[] prices) {int ans = 0;int n = prices.Length;for (int i = 1; i < n; ++i) {int diffPrice=prices[i] - prices[i - 1];if(diffPrice>0){ans += diffPrice;}}return ans;}
}
2.1.2. 算法思路与步骤
只要后一天的价格比今天高,那么我今天就买,后一天就卖。

2.1.3. 算法复杂度
- 时间复杂度: O ( n ) O(n) O(n)
- 空间复杂度: O ( 1 ) = 2 O(1)=2 O(1)=2
2.2. 动态规划算法
2.2.1. 算法代码
public class Solution {public int MaxProfit(int[] prices) {if (prices.Length < 2) {return 0;}int[] OwnStocks=new int[prices.Length];int[] NoStocks=new int[prices.Length];OwnStocks[0]=-prices[0];NoStocks[0]=0;for(int i=1;i<prices.Length;i++){OwnStocks[i]=Math.Max(OwnStocks[i-1],NoStocks[i-1]-prices[i]);NoStocks[i]=Math.Max(NoStocks[i-1],OwnStocks[i-1]+prices[i]);}return NoStocks[prices.Length-1];}
}
2.2.2. 算法思路与步骤
- 由于不可以同时存在多支股票,所以每天只有可能有两种状态
有股票、没有股票 - 第一天存在股票=0-第一天股票价值;第一天不存在股票=0(没有购买或者当天售出)
- 后续每一天,
当天有股票的最大利益=Math.Max(前一天有股票的值,前一天没有股票的值-当天股票值[购买股票]) - 后续每一天,
当前没有股票的最大利益=Math.Max(前一天没有股票的值,前一天有股票的值+当天股票值[卖出股票]`)
图解如下:

2.2.3. 算法复杂度
- 时间复杂度: O ( n ) O(n) O(n)
- 空间复杂度: O ( n ) = 2 n O(n)=2n O(n)=2n
2.3. 123. 买卖股票的最佳时机 III

2.3.1. 动态规划算法
这一题就和第二题的动态规划类似,只是第二题是两个状态,而第三题是四个状态。
没有买入第一次买入,没有卖出第一次买出,没有卖入第二次买入,没有卖出第二次买出
由于没有买入全程是0所以不做考虑,列出了5种,但实际上只有4种状态。
2.3.2. 算法代码
public class Solution {public int MaxProfit(int[] prices) {if(prices.Length<2){return 0;}int oneBuy=-prices[0];int oneSale=0;int twoBuy=-prices[0];int twoSale=0;for(int i=1;i<prices.Length;i++){oneBuy=Math.Max(oneBuy,-prices[i]);oneSale=Math.Max(oneSale,oneBuy+prices[i]);twoBuy=Math.Max(twoBuy,oneSale-prices[i]);twoSale=Math.Max(twoSale,twoBuy+prices[i]);}return twoSale;}
}
2.3.3. 算法复杂度
- 时间复杂度: O ( n ) O(n) O(n)
- 空间复杂度: O ( 1 ) = 4 O(1)=4 O(1)=4
相关文章:

我在leetcode用动态规划炒股
事情是这样的,突然兴起的我在letcode刷题 121. 买卖股票的最佳时机122. 买卖股票的最佳时机 II123. 买卖股票的最佳时机 III 以上三题。 1. 121. 买卖股票的最佳时机 1.1. 暴力遍历,两次遍历 1.1.1. 算法代码 public class Solution {public int Ma…...

rust实践-异步并发socket通信
客户端 [package] name = "rust_client" version = "0.1.0" edition = "2021"[dependencies] tokio = {version = "1.14.0", features = ["full"] }use tokio::io::{self, AsyncReadExt, AsyncWriteExt}; use tokio::net::…...

SolidUI社区-根据Prompt打造人设
背景 随着文本生成图像的语言模型兴起,SolidUI想帮人们快速构建可视化工具,可视化内容包括2D,3D,3D场景,从而快速构三维数据演示场景。SolidUI 是一个创新的项目,旨在将自然语言处理(NLP)与计算机图形学相…...
设计模式行为型——观察者模式
目录 什么是观察者模式 观察者模式的实现 观察者模式角色 观察者模式类图 观察者模式举例 观察者模式代码实现 观察者模式的特点 优点 缺点 使用场景 注意事项 实际应用 什么是观察者模式 观察者模式(Observer Pattern)是一种行为型设计模式…...

Kernel Exception导致手机重启案例分析
和你一起终身学习,这里是程序员Android 经典好文推荐,通过阅读本文,您将收获以下知识点: 一、高温触发 Kernel Exception 重启问题二、解决方案三、提高电池温度方案 一、 高温触发 Kernel Exception 重启问题 手机 电池温度 默认60度以上高温…...
C++入门篇5---模板
相信大家都遇到过这么一种情况,为了满足不同类型的需求,我们要写多个功能相同,参数类型不同的代码,为此,C引入了泛型编程这一概念,而模板就是实现泛型编程的基础,其实本质就是我们写一个类似”模…...

L2CS-Net: 3D gaze estimation
L2CS-Net: Fine-Grained Gaze Estimation in Unconstrained Environments论文解析 摘要1. 简介2. Related Work3. METHOD3.1 Proposed loss function3.2 L2CS-Net 结构3.3 数据集3.4 评价指标 4. 实验4.1 实验结果 论文地址:L2CS-Net: Fine-Grained Gaze Estimation…...

kenernetes/k8s笔试面试
k8s的基础概念 k8s本质是一个容器编排系统,可以管理容器的生命周期,应用部署,更新,维护,应用提供服务,扩容缩容应用,故障自愈。 k8s与docker的关系 docker:是一种轻量级的虚拟化技术。运维层…...

我们真的是在做数据治理吗
我们真的是在做数据治理吗? 什么是数据治理? 数据治理和数据管理有什么区别? 相信即使是考过数据治理工程师的人,面对这2个问题也仍然会有这个疑问。 目前国际和国内对于数据治理没有明确统一的定义,对于数据治理的服…...

聊聊汽车电子的话题
当谈到汽车电子时,有许多有趣的话题可以探讨。以下是一些可能感兴趣的话题: 自动驾驶技术:自动驾驶技术正变得越来越先进,它们如何在汽车中实现?它们将如何改变我们的交通方式以及对道路安全的影响? 电动汽…...

ThinkPHP6企业OA办公系统
有需要请加文章底部Q哦 可远程调试 ThinkPHP6企业OA办公系统 一 介绍 勾股OA基于ThinkPHP6开发,前端Layui,数据库mysql,是一款实用的企业办公系统。可多角色登录,集成了系统设置、人事管理、消息管理、审批管理、日常办公、客户…...
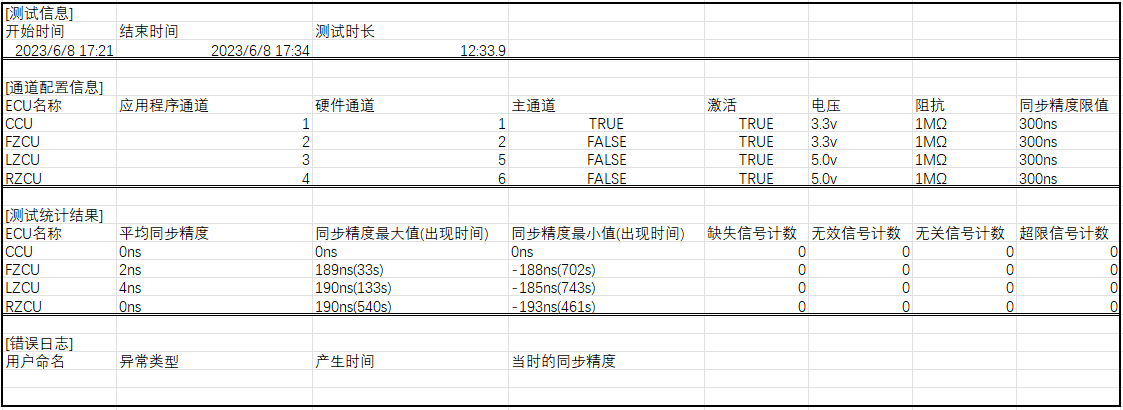
PPS Tester测量原理和实施方法
怿星科技发布了新品PPS Tester,这是一款基于1PPS方法的时间同步精度测试设备。PPS Tester由硬件模块ETS2110和上位机软件ePPSTester构成。本文将围绕此设备的应用场景,介绍相关概念和设备使用方法。 什么是时间同步? 时间同步就是采取某项技…...
浅谈新电改背景下电网企业综合能源服务商业模式研究及发展方向
安科瑞 华楠 摘要: 新电改方案实施后,由于输配电价的改革和售电侧的放开,电网企业的盈利模式也随之发生了变化。这就要求电网企业转变服务理念与经营方式,来寻求竞争优势。基于“魏朱六要素商业模式”模型,对电网企业综合能源服务…...

SpringBoot + Docker 实现一次构建到处运行~
一、容器化部署的好处 图片 Docker 作为一种新兴的虚拟化方式,它可以更高效的利用系统资源,不需要进行硬件虚拟以及运行完整操作系统等额外开销。 传统的虚拟机技术启动应用服务往往需要数分钟,而 Docker 容器应用,由于直接运行…...

clang-format格式化代码
1. clang-format简介 Clang-Format可用于格式化(排版)多种不同语言的代码。其自带的排版格式主要有:LLVM, Google, Chromium, Mozilla, WebKit等; 利用style参数配置风格。通过编写 .clang-format 文件,可以实现代码风格的配置。…...

品牌宣传与媒体传播是声誉管理的主要方式之一
企业声誉是现如今影响品牌信任度、客户忠诚度的重要因素,也被视为企业的一种无形资,更影响着企业未来的发展。因此,企业声誉管理也日渐成为企业管理的重要课题之一,尤其在品牌营销管理领域。 什么是声誉管理?声誉管理有…...
)
2023年8月7日-8月13日,(上午熟悉公司代码,周一到周五晚上优先工作所急视频教程,其他业余时间进行ue视频教程,为独立游戏做准备)
按照规划,上午熟悉公司源码,下午进行filament和ue渲染,晚上写工作代码。回家后泛读pbrt或者其他书籍催眠。 业余学习ue的各种视频教程,为独立游戏做准备(公司也实行末位淘汰,给自己留条后路)。累…...

Vue3 第二节 Vue3的响应式
1.Vue3的响应式原理 2.ref函数和reactive函数的对比 3.setup注意点 一.Vue3的响应式原理 1.Vue2.x中的响应式原理 ① 实现原理 对象类型:通过Object.defineProperty() 对属性的读取,修改进行拦截(数据劫持)数组类型…...
通过easyui实现动态控制表格字段显示、导出表格数据
前言 学过layui前端框架的都知道,layui默认帮我们实现了控制表格字段显示以及数据的导出功能。 1、控制表格字段显示 2、数据导出 3、导出为pdf:导出按钮的右边那个按钮就是打印pdf的 那么,easyui要怎么实现这些功能呢?这篇文章就…...

JWT入门,jwt可以解密吗?
JWT 什么是 JWT JSON Web Token,通过数字签名的方式,以 JSON 对象为载体,在不同的服务终端之间安全地传输信息 官网:https://jwt.io/SDK: https://jwt.io/libraries (含Java和各种语言)Java SDK(上面的SDK链接得到): https://g…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...

并发编程 - go版
1.并发编程基础概念 进程和线程 A. 进程是程序在操作系统中的一次执行过程,系统进行资源分配和调度的一个独立单位。B. 线程是进程的一个执行实体,是CPU调度和分派的基本单位,它是比进程更小的能独立运行的基本单位。C.一个进程可以创建和撤销多个线程;同一个进程中…...

基于Java+VUE+MariaDB实现(Web)仿小米商城
仿小米商城 环境安装 nodejs maven JDK11 运行 mvn clean install -DskipTestscd adminmvn spring-boot:runcd ../webmvn spring-boot:runcd ../xiaomi-store-admin-vuenpm installnpm run servecd ../xiaomi-store-vuenpm installnpm run serve 注意:运行前…...

在树莓派上添加音频输入设备的几种方法
在树莓派上添加音频输入设备可以通过以下步骤完成,具体方法取决于设备类型(如USB麦克风、3.5mm接口麦克风或HDMI音频输入)。以下是详细指南: 1. 连接音频输入设备 USB麦克风/声卡:直接插入树莓派的USB接口。3.5mm麦克…...
