当前位置： 首页 > news >正文

ExpressJS教程_编程入门自学教程_菜鸟教程-免费教程分享

news 2026/2/10 0:18:33

教程简介

Express是基于Node.js平台,快速、开放、极简的Web开发框架；通俗的理解:Express的作用和Node.js内置的http模块类似,是专门用来创建Web服务器的；Express的本质:就是一个npm上的第三方包,提供了快速创建Web服务器的便捷方法。ExpressJS是一个Web应用程序框架，为您提供构建网站，Web应用程序和后端的简单API。 使用ExpressJS，您无需担心低级协议，进程等。

ExpressJS入门教程 - 从概述，环境，Hello World，路由，HTTP方法，URL构建，中间件，模板，静态文件，表单数据，数据库，Cookie，身份验证，会话，RESTful API，脚手架，错误处理，调试，了解ExpressJS，最佳实践，资源。

教程目录

  • ExpressJS - 概述
  • ExpressJS - 环境
  • ExpressJS - Hello World
  • ExpressJS - 路由
  • ExpressJS - HTTP方法
  • ExpressJS - URL构建
  • ExpressJS - 中间件
  • ExpressJS - 模板
  • ExpressJS - 提供静态文件
  • ExpressJS - 表格数据
  • ExpressJS - 数据库
  • ExpressJS - Cookies
  • ExpressJS - 会话
  • ExpressJS - 身份验证
  • ExpressJS - RESTFul API
  • ExpressJS - Scaffolding
  • ExpressJS - 错误处理
  • ExpressJS - 调试
  • ExpressJS - 最佳实践
  • ExpressJS - 资源
  • ExpressJS - 有用的资源

相关文章：

ExpressJS教程_编程入门自学教程_菜鸟教程-免费教程分享

教程简介 Express是基于Node.js平台,快速、开放、极简的Web开发框架；通俗的理解:Express的作用和Node.js内置的http模块类似,是专门用来创建Web服务器的；Express的本质:就是一个npm上的第三方包,提供了快速创建Web服务器的便捷方法。ExpressJS是一个Web…...

编程日记 2023/8/8 12:45:14

时序预测 | MATLAB实现BO-BiLSTM贝叶斯优化双向长短期记忆神经网络时间序列预测

时序预测 | MATLAB实现BO-BiLSTM贝叶斯优化双向长短期记忆神经网络时间序列预测 目录 时序预测 | MATLAB实现BO-BiLSTM贝叶斯优化双向长短期记忆神经网络时间序列预测效果一览基本介绍模型搭建程序设计参考资料 效果一览 基本介绍 MATLAB实现BO-BiLSTM贝叶斯优化双向长短期记忆…...

编程日记 2023/8/8 12:44:13

HIVE优化之不需要参数优化

#1.数据倾斜 什么是数据倾斜？ 一部分数据多 一部分数据少 造成的结果： MR运行过慢 主要是shuffle和reduce过程慢 分组聚合导致数据倾斜 Hive未优化的分组聚合 方法1：在MAP端直接聚合（分组聚合优化），减少…...

编程日记 2023/8/8 12:43:11

前端 select 标签如何创建下拉菜单？

聚沙成塔每天进步一点点 ⭐ 专栏简介⭐ 代码示例⭐ 代码讲解⭐ 写在最后 ⭐ 专栏简介 前端入门之旅：探索Web开发的奇妙世界 记得点击上方或者右侧链接订阅本专栏哦 几何带你启航前端之旅 欢迎来到前端入门之旅！这个专栏是为那些对Web开发感兴趣、刚刚踏…...

编程日记 2023/8/8 12:42:10

基于 eclipse-temurin 构建国内时区，地区，语言的docker镜像

基于 eclipse-temurin 构建国内时区，地区，语言的镜像 使用场景自定Dockerfile构建自己的基础镜像构建本地镜像推送远程仓库 使用场景 在给应用构建自定义镜像时，往往需要在每次构建时去调整时区，地区这些东西；每次构建…...

编程日记 2023/8/8 12:41:08

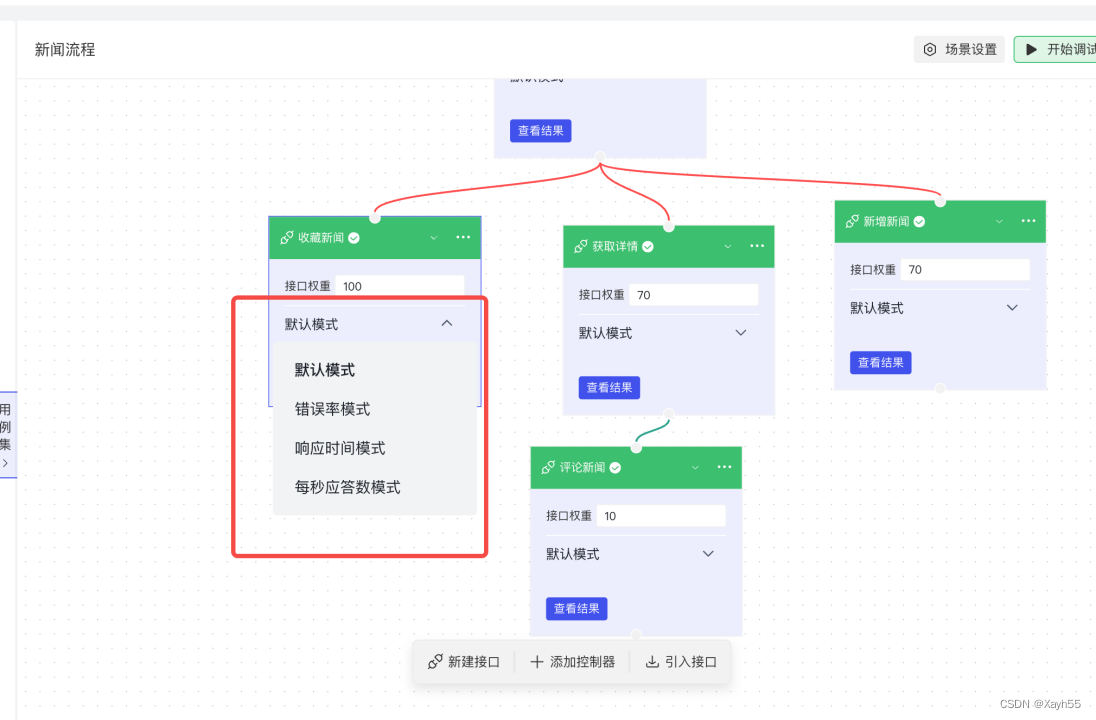
RunnerGo配置场景时接口模式该怎么选

在进行性能测试时，测试场景的正确配置非常关键。首先，需要根据业务场景和需求，设计出合理的测试场景，再利用相应的工具进行配置，实现自动化的性能测试。 在JMeter中，用户需要自己组织测试场景，…...

编程日记 2023/8/8 12:40:06

系统分享UIActivity

iOS自带的分享控件可以完成绝大部分的分享需求。 它可以不需要集成微信、QQ等第三方SDK就可以实现分享（需要在弹出视图里面点击更多打开开关）到微信好友、朋友圈等,功能很强大，也很方便。 一、系统分享两个步骤 UIActivity配置分享的内容和…...

编程日记 2023/8/8 12:39:05

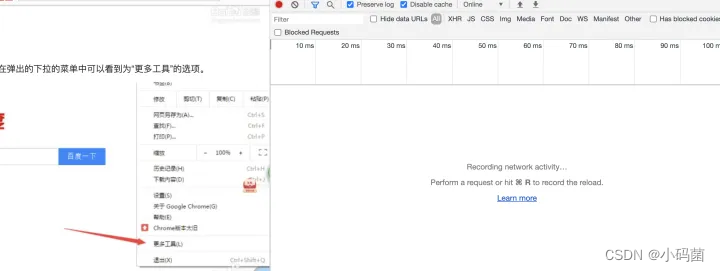
常用抓包工具

Fiddler Fiddler 是一个很好用的抓包工具，可以用于抓取http/https的数据包，常用于Windows系统的抓包，它有个优势就是免费 Charles Charles是由JAVA开发的，可以运行在window Linux MacOS，但它是收费的，和…...

编程日记 2023/8/8 12:38:03

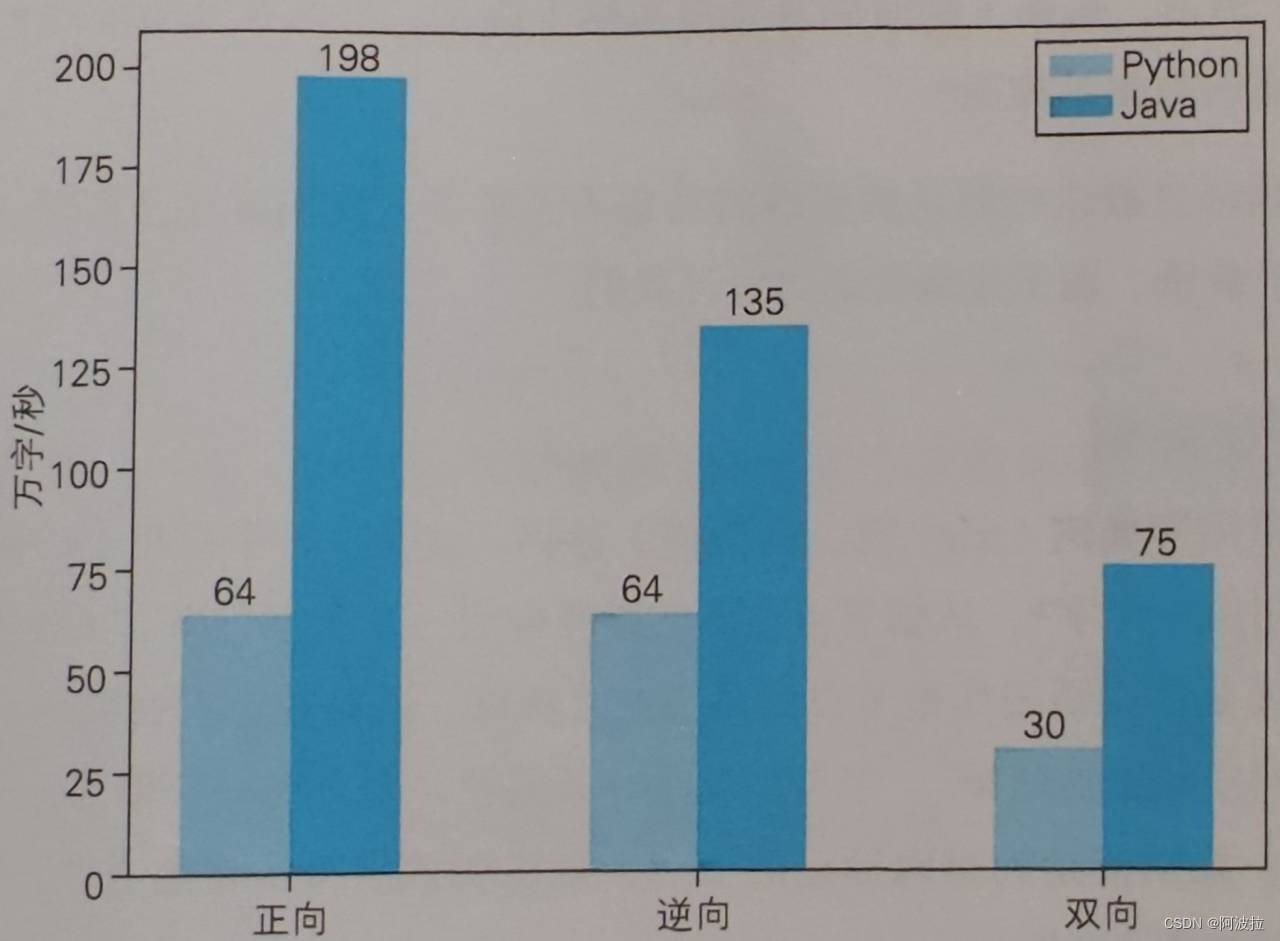
自然语言处理学习笔记（五）————切分算法

目录 1.切分算法 2.完全切分 3.正向最长匹配 4.逆向最长匹配 5.双向最长匹配 6.速度评测 1.切分算法 词典确定后，句子可能含有很多词典中的词语，他们有可能互相重叠，如何切分需要一些规则。常用规则为：正向匹配算法、逆向匹…...

编程日记 2023/8/8 12:37:02

SQL-方法论

写SQL时可以考虑的手段： 行转列 先分为多个临时表，然后JOIN到一起 select uid,t1.name YuWen,t2.name ShuXue from (select uid,namefrom tableAwhere naem 语文) t1join (select uid,namefrom tableAwhere naem 数学) t2on t1.uid t2.uid; 用sum(if…...

编程日记 2023/8/8 12:36:01

[Python从零到壹] 六十八.图像识别及经典案例篇之图像特效（毛玻璃、浮雕、油漆和模糊特效变换）

八月太忙，还是写一篇吧！ 欢迎大家来到“Python从零到壹”，在这里我将分享约200篇Python系列文章，带大家一起去学习和玩耍，看看Python这个有趣的世界。所有文章都将结合案例、代码和作者的经验讲解，真心想把自己近十年的编程经验分享给大家，希望对您有所帮助，文章中不足…...

编程日记 2023/8/8 12:34:55

undefined与null的区别

null 表示一个对象被定义了，值为“空值” undefined 表示不存在这个值 1.undefined typeof undefined //"undefined" undefined 是一个表示"无"的原始值或者说表示"缺少值"，就是此处应该有一个值，但还没有…...

编程日记 2023/8/8 12:33:54

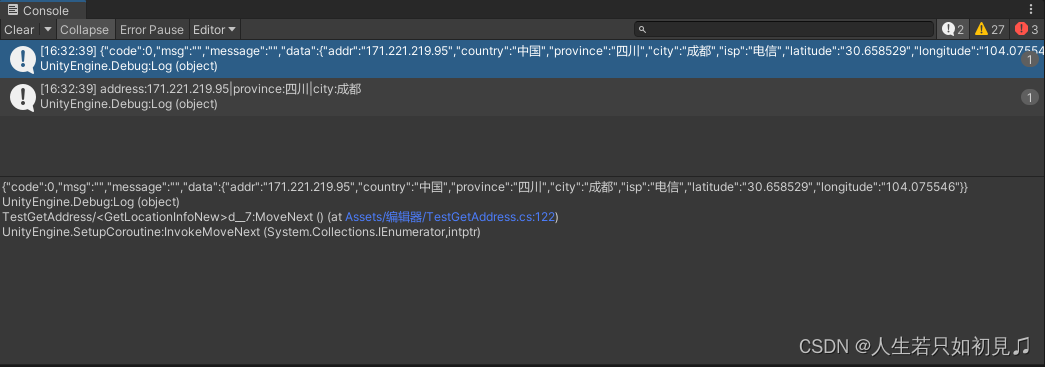
Unity之获取用户地理位置

1.直接利用三方API获取： 1.1 利用bilibili的api 【未知稳定性】 public void Awake() {StartCoroutine(GetLocationInfoNew());}/// <summary>/// 利用bilibili的接口通过ip直接获取城市信息/// </summary>IEnumerator GetLocationInfoNew() {//UnityWebRequest …...

编程日记 2023/8/8 12:32:53

TC3XX - MCAL知识点（二十）：CAN MCAL配置及代码实战（CAN/CANFD/extenen CAN）

目录 1、概述 2、MCAL配置 2.1、实验目标 2.2、CAN配置（包含CAN与CANFD） 2.2.1、CanGeneral...

编程日记 2023/8/8 12:31:50

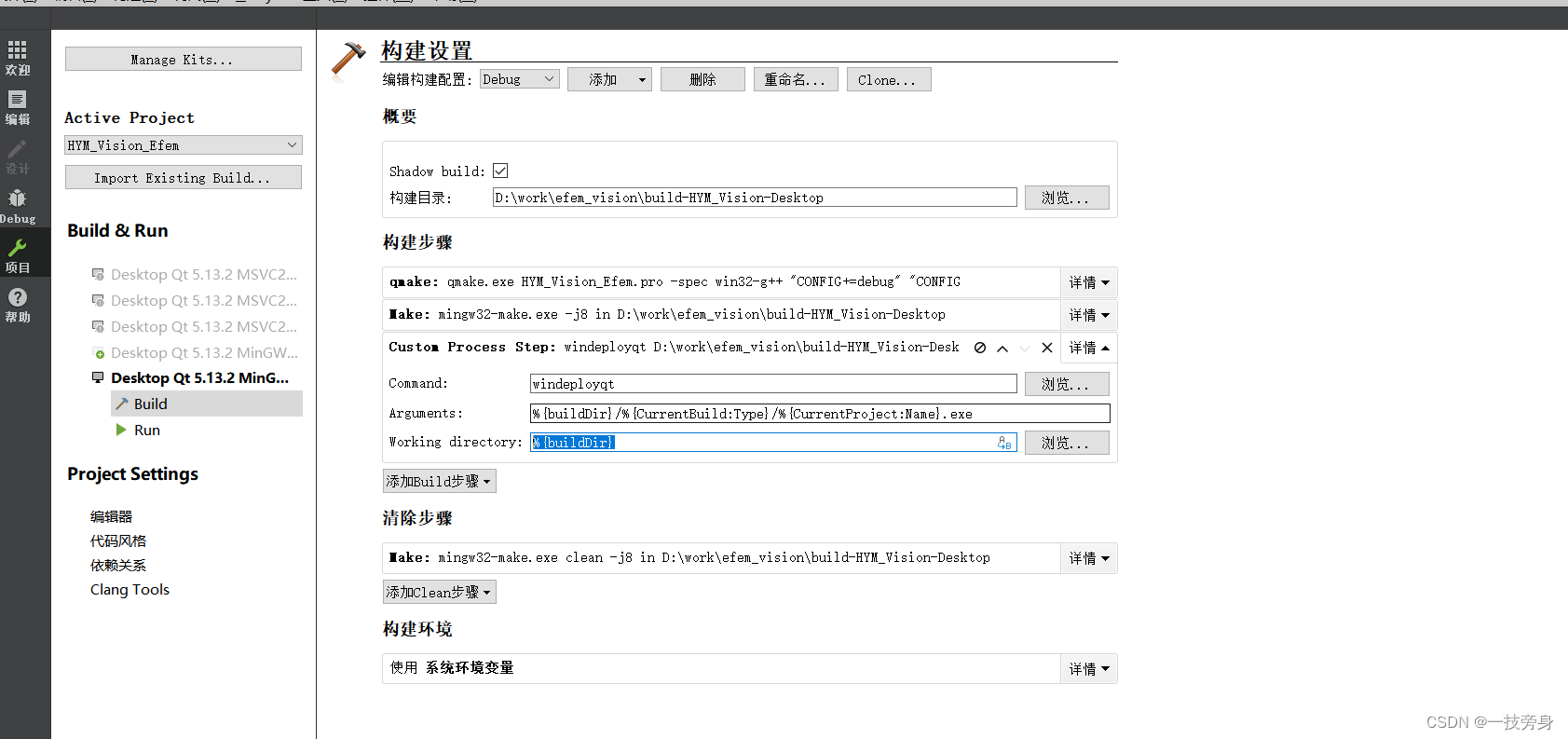
QT生成Debug和Release发布版后，运行exe缺少dll问题

在QT Creator生成debug和release的exe执行文件后&#xff0c;运行时&#xff0c;报错缺少*.dll.解决办法1&#xff1a; 在系统环境变量中添加D:\Qt\Qt5.13.2\Tools\mingw730_64\bin后&#xff0c;即可运行。 当使用此方法时&#xff0c;将exe拷贝到其他电脑中运行时&#xff0c…...

编程日记 2023/8/8 12:30:49

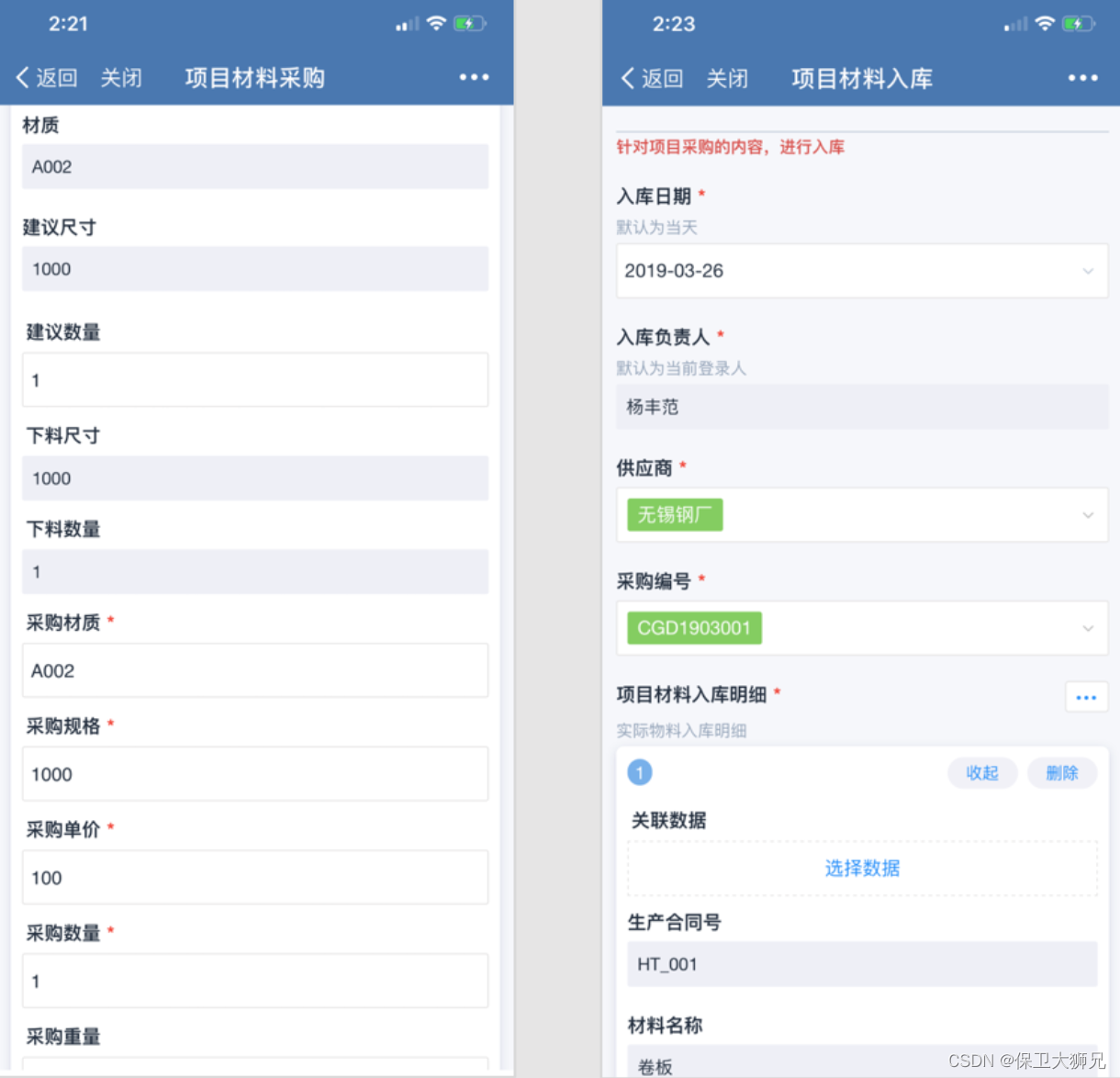
企业进销存管理流程有哪些? 附进销存管理系统

阅读本文&#xff0c;您可以了解&#xff1a;1、进销存的定义&#xff1b;2、进销存的流程 首先&#xff0c;在了解进销存流程之前&#xff0c;我们必须厘清一个问题&#xff1f; 什么是进销存&#xff1f; 进销存是一个企业管理中常用的术语&#xff0c;是指企业在经营过程中…...

编程日记 2023/8/8 12:29:48

RPC原理与Go RPC详解

文章目录 RPC原理与Go RPC什么是RPC本地调用RPC调用HTTP调用RESTful API net/rpc基础RPC示例基于TCP协议的RPC使用JSON协议的RPCPython调用RPC RPC原理 RPC原理与Go RPC 什么是RPC RPC&#xff08;Remote Procedure Call&#xff09;&#xff0c;即远程过程调用。它允许像调用…...

编程日记 2023/8/8 12:28:47

JavaScript:异步编程的发展

在JavaScript编程中&#xff0c;异步编程是处理耗时操作的关键技术&#xff0c;它允许程序在等待某些操作完成时继续执行其他任务&#xff0c;提高了程序的性能和响应性。随着技术的发展&#xff0c;JavaScript的异步编程模型也在不断演进&#xff0c;从最初的回调函数到现在的…...

编程日记 2023/8/8 12:27:45

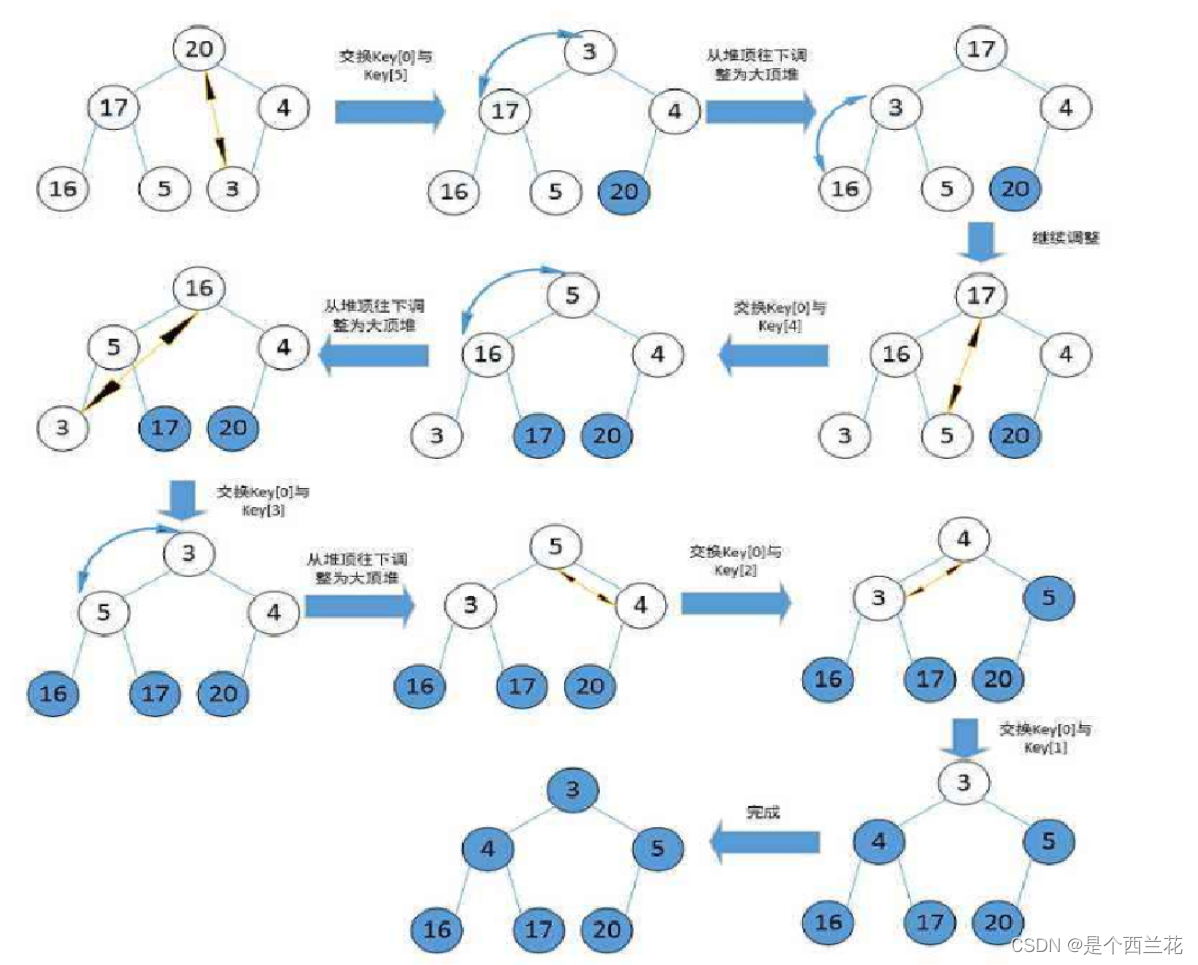
排序第二课【选择排序】直接选择排序 与 堆排序

目录 1. 排序的概念&#xff1a; 2.选择排序的基本思想 3.直接选择排序 4.堆排序 1. 排序的概念&#xff1a; 排序&#xff1a;所谓排序&#xff0c;就是使一串记录&#xff0c;按照其中的某个或某些关键字的大小&#xff0c;递增或递减的排列起来的操作。 稳定性&#xf…...

编程日记 2023/8/8 12:25:36

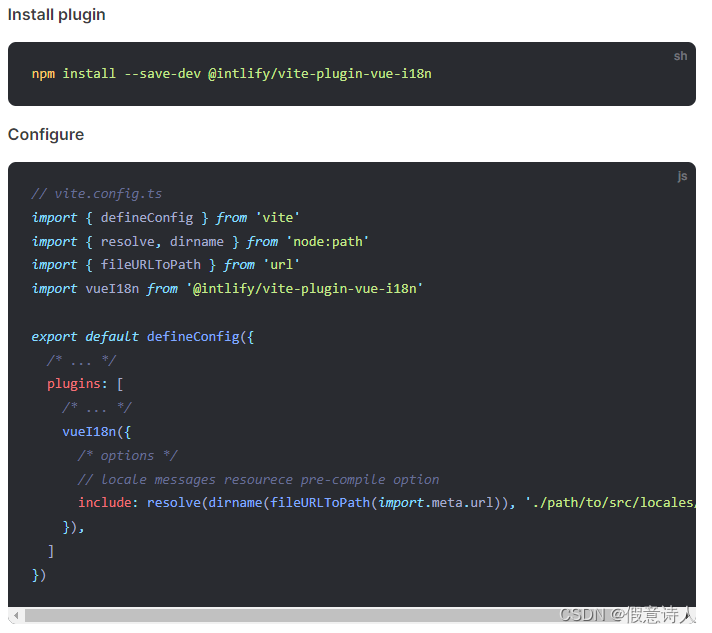
【chrome扩展开发】vue-i18n使用问题及解决方案

记录chrome扩展开发时调用vue-i18n的一些问题和解决方法 环境 vue: ^3.3.4vue-i18n: ^9.2.2vite: ^4.4.8 错误1 Uncaught (in promise) EvalError: Refused to evaluate a string as JavaScript because unsafe-eval is not an allowed source of script in the following Con…...

编程日记 2023/8/8 12:24:33

Debian系统简介

目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版&#xff…...

编程新知 2026/2/1 13:41:09

基础测试工具使用经验

背景 vtune&#xff0c;perf, nsight system等基础测试工具&#xff0c;都是用过的&#xff0c;但是没有记录&#xff0c;都逐渐忘了。所以写这篇博客总结记录一下&#xff0c;只要以后发现新的用法&#xff0c;就记得来编辑补充一下 perf 比较基础的用法&#xff1a; 先改这…...

编程新知 2025/11/22 7:38:58

Spring Boot+Neo4j知识图谱实战：3步搭建智能关系网络！

一、引言 在数据驱动的背景下&#xff0c;知识图谱凭借其高效的信息组织能力&#xff0c;正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合&#xff0c;探讨知识图谱开发的实现细节&#xff0c;帮助读者掌握该技术栈在实际项目中的落地方法。 …...

编程新知 2025/9/17 21:39:04

Ascend NPU上适配Step-Audio模型

1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统&#xff0c;支持多语言对话&#xff08;如 中文&#xff0c;英文&#xff0c;日语&#xff09;&#xff0c;语音情感&#xff08;如 开心&#xff0c;悲伤&#xff09;&#x…...

编程新知 2026/1/31 4:37:39

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码： prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

编程新知 2025/7/4 0:50:01

Java毕业设计：WML信息查询与后端信息发布系统开发

JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发&#xff0c;实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构&#xff0c;服务器端使用Java Servlet处理请求&#xff0c;数据库采用MySQL存储信息&#xff0…...

编程新知 2025/10/27 13:29:11

Windows安装Miniconda

一、下载 https://www.anaconda.com/download/success 二、安装 三、配置镜像源 Anaconda/Miniconda pip 配置清华镜像源_anaconda配置清华源-CSDN博客 四、常用操作命令 Anaconda/Miniconda 基本操作命令_miniconda创建环境命令-CSDN博客...

编程新知 2026/1/31 7:39:20

Unity VR/MR开发-VR开发与传统3D开发的差异

视频讲解链接&#xff1a;【XR马斯维】VR/MR开发与传统3D开发的差异【UnityVR/MR开发教程--入门】_哔哩哔哩_bilibili...

编程新知 2026/2/5 4:00:33

《信号与系统》第 6 章 信号与系统的时域和频域特性

目录 6.0 引言 6.1 傅里叶变换的模和相位表示 6.2 线性时不变系统频率响应的模和相位表示 6.2.1 线性与非线性相位 6.2.2 群时延 6.2.3 对数模和相位图 6.3 理想频率选择性滤波器的时域特性 6.4 非理想滤波器的时域和频域特性讨论 6.5 一阶与二阶连续时间系统 6.5.1 …...

编程新知 2026/2/5 4:45:50

跨平台商品数据接口的标准化与规范化发展路径：淘宝京东拼多多的最新实践

在电商行业蓬勃发展的当下&#xff0c;多平台运营已成为众多商家的必然选择。然而&#xff0c;不同电商平台在商品数据接口方面存在差异&#xff0c;导致商家在跨平台运营时面临诸多挑战&#xff0c;如数据对接困难、运营效率低下、用户体验不一致等。跨平台商品数据接口的标准…...

编程新知 2026/1/26 10:30:17