机器学习基础08-回归算法矩阵分析(基于波士顿房价(Boston House Price)数据集)
回归算法通常涉及到使用矩阵来表示数据和模型参数。线性回归是最常见的回归算法之一,它可以用矩阵形式来表示。
考虑一个简单的线性回归模型: y = m x + b y = mx + b y=mx+b,其中 y y y 是因变量, x x x 是自变量, m m m 是斜率, b b b 是截距。将这个模型表示成矩阵形式,可以如下所示:
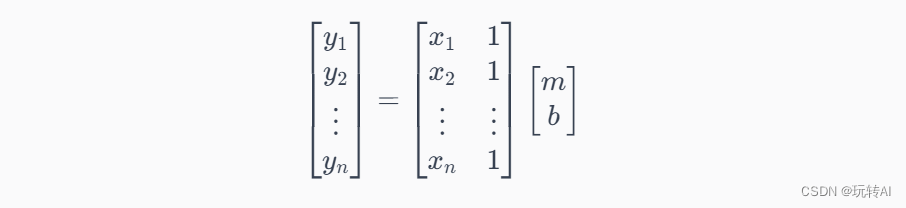
在上面的矩阵表达中,左边的矩阵表示因变量 y y y,右边的矩阵表示自变量 x x x 和一个常数项 1 1 1。而模型参数 m m m 和 b b b 则以矩阵的形式表示。
通过最小化残差(观测值与模型预测值之间的差异)来确定最佳的参数 m m m 和 b b b,这通常涉及到矩阵计算中的求解方法,如最小二乘法。
其他更复杂的回归算法,例如多变量线性回归、岭回归、Lasso回归等,也可以通过矩阵表示来进行推导和求解。矩阵表示使得回归算法的计算更加紧凑和易于理解。
接下来将介绍三种评估机器学习的回归算法的评估矩阵。
- 平均绝对误差(Mean Absolute Error,MAE)。
- 均方误差(Mean Squared Error,MSE)。
- 决定系数(R2)。
示例中采用将使用波士顿房价(Boston House Price)数据集进行实验操作
数据集下载地址
https://github.com/selva86/datasets/blob/master/BostonHousing.csv
数据集介绍:
波士顿房价预测更像是预测一个连续值,当然这也是一个非常经典的机器学习案例
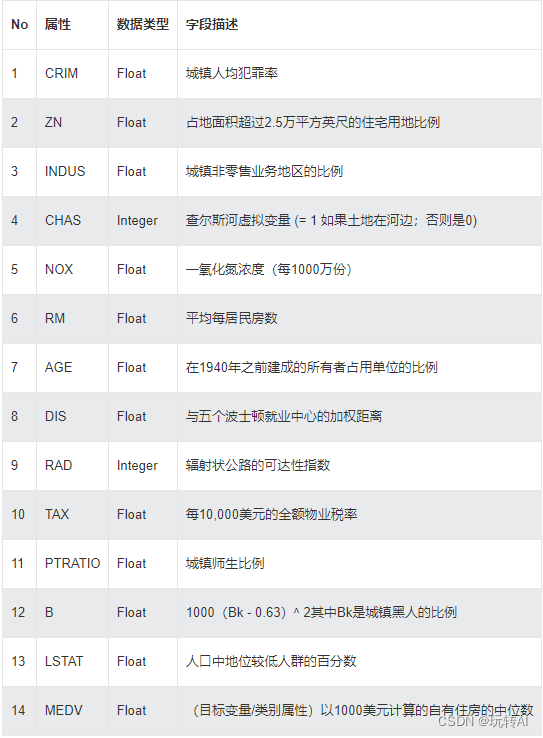
平均绝对误差
平均绝对误差是所有单个观测值与算术平均值的偏差的绝对值的平均值。与平均误差相比,平均绝对误差由于离差被绝对值化,不会出现正负相抵消的情况,因而,平均绝对误差能更好地反映预测值误差的实际情况。
代码如下:
import pandas as pd
from sklearn.linear_model import LinearRegressionfrom sklearn.model_selection import KFold, cross_val_score#数据预处理
path = 'D:\down\\BostonHousing.csv'
data = pd.read_csv(path)array = data.valuesX = array[:, 0:13]
Y = array[:, 13]n_splits = 10seed = 7kflod = KFold(n_splits=n_splits, random_state=seed, shuffle=True)
#
model = LinearRegression()scoring = 'neg_mean_absolute_error'results = cross_val_score(model, X, Y, cv=kflod, scoring=scoring)print("MSE: %.3f (%.3f)" % (results.mean(), results.std()))执行结果如下:
MSE: -3.387 (0.667)
均方误差
均方误差是衡量平均误差的方法,可以评价数据的变化程度。均方根误差是均方误差的算术平方根。均方误差的值越小,说明用该预测模型描述实验数据的准确度越高。
代码如下:
import pandas as pd
from sklearn.linear_model import LinearRegressionfrom sklearn.model_selection import KFold, cross_val_score#数据预处理
path = 'D:\down\\BostonHousing.csv'
data = pd.read_csv(path)array = data.valuesX = array[:, 0:13]
Y = array[:, 13]n_splits = 10seed = 7kflod = KFold(n_splits=n_splits, random_state=seed, shuffle=True)
#
model = LinearRegression()scoring = 'neg_mean_squared_error'results = cross_val_score(model, X, Y, cv=kflod, scoring=scoring)print("MSE: %.3f (%.3f)" % (results.mean(), results.std()))运行结果如下:
MSE: -23.747 (11.143)
决定系数(R2)
决定系数,反映因变量的全部变异能通过回归关系被自变量解释的比例。拟合优度越大,自变量对因变量的解释程度越高,自变量引起的变动占总变动的百分比越高,观察点在回归直线附近越密集。
如R2为0.8,则表示回归关系可以解释因变量80%的变异。换句话说,如果我们能控制自变量不变,则因变量的变异程度会减少80%。
决定系数(R2)的特点:
- 可决系数是非负的统计量。
- 可决系数的取值范围:0≤R2≤1。
- 可决系数是样本观测值的函数,是因随机抽样而变动的随机变量。为
此,对可决系数的统计的可靠性也应进行检验。
代码如下:
import pandas as pd
from sklearn.linear_model import LinearRegressionfrom sklearn.model_selection import KFold, cross_val_score#数据预处理
path = 'D:\down\\BostonHousing.csv'
data = pd.read_csv(path)array = data.valuesX = array[:, 0:13]
Y = array[:, 13]n_splits = 10seed = 7kflod = KFold(n_splits=n_splits, random_state=seed, shuffle=True)
#
model = LinearRegression()scoring = 'r2'results = cross_val_score(model, X, Y, cv=kflod, scoring=scoring)print("R2: %.3f (%.3f)" % (results.mean(), results.std()))执行结果如下:
R2: 0.718 (0.099)
通常情况下,R2(也称为决定系数)是用来衡量一个回归模型的拟合优度的指标。它的取值范围在0到1之间,越接近1表示模型拟合得越好,越接近0表示模型拟合较差。
在这个结果中,“R2: 0.718” 表示模型的拟合优度为0.718,大致可以理解为模型解释了目标变量约71.8%的方差。而 “(0.099)” 则是标准误差的信息,用于表示R2的置信区间。
相关文章:

机器学习基础08-回归算法矩阵分析(基于波士顿房价(Boston House Price)数据集)
回归算法通常涉及到使用矩阵来表示数据和模型参数。线性回归是最常见的回归算法之一,它可以用矩阵形式来表示。 考虑一个简单的线性回归模型: y m x b y mx b ymxb,其中 y y y 是因变量, x x x 是自变量, m m m 是…...

[英语单词] password, passphrase, passport.... paraphrase
password 是密码,大多可能就是一个单词的量,10多个字母,或者更少;而且就是一个单词; 后来发现密码这么设置不安全,怎么办? 就出现了passphrase,使用词组的组合来做为密码,…...
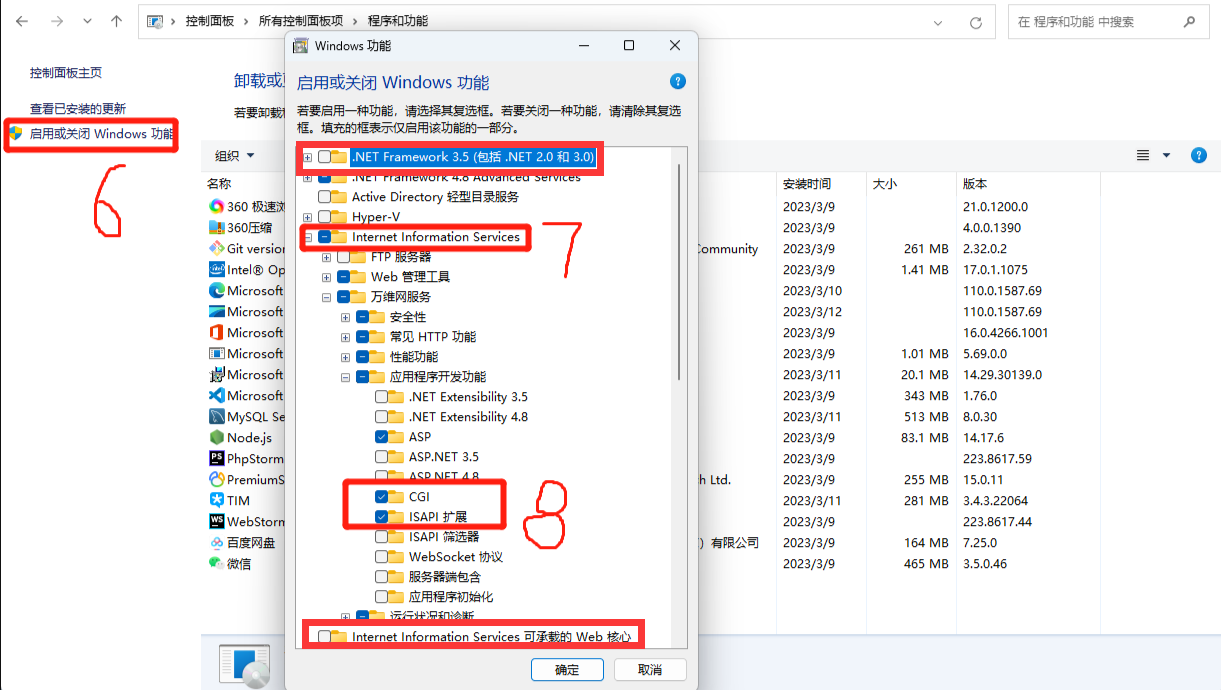
windows(iis)服务器部署安装wordpress(php)网站教程
该教程包含iis安装,php安装,mysql安装,php网站部署上线,windows服务部署php网站,只需要这一篇文章就够了。 该教程为iis服务器部署安装wordpress(php)网站教程,同样适用wordpress网站迁移。 配置要求 1、windows服务器安装iis windows服务器安装iis管理器 打开控制面…...

ETCD备份还原
备份只需要在一个节点上备就可以了,每个节点上的数据是同步的;但是数据恢复是需要在每个主节点上进行 1.查看证书位置 #查看etcd证书 [rootk8s-master01 manifests]# cat /etc/kubernetes/manifests/kube-apiserver.yaml |grep etcd- --etcd-cafile/et…...

探索CSS计数器:优雅管理网页元素的计数与序号
113. 探索CSS计数器:优雅管理网页元素的计数与序号 在前端开发中,我们经常需要对网页元素进行计数与序号,如有序列表、表格行号、步骤指示等。为了优雅地管理这些计数与序号,CSS提供了一种强大的功能:CSS计数器&#…...

这次一次性通关channel!
一 前言 前几天面试某大厂的云原生岗位,原本是一个轻松愉快的过程,当问到第二个问题,我就发现事情的不对劲,先复盘一下面试官有关Channel的问题,然后再逐一解决,最后进行扩展,这次一定要一次性…...

线程数控制
项目需求:javaMATLAB并行开发 在java中调用由MATLAB转成的jar包的代码,需要调用到底层的MATLAB服务。每次只能一个线程调用,当多个线程同时调用MATLAB时,MATLAB会报错。导致整个java服务挂掉。 现在增加线程控制,每…...
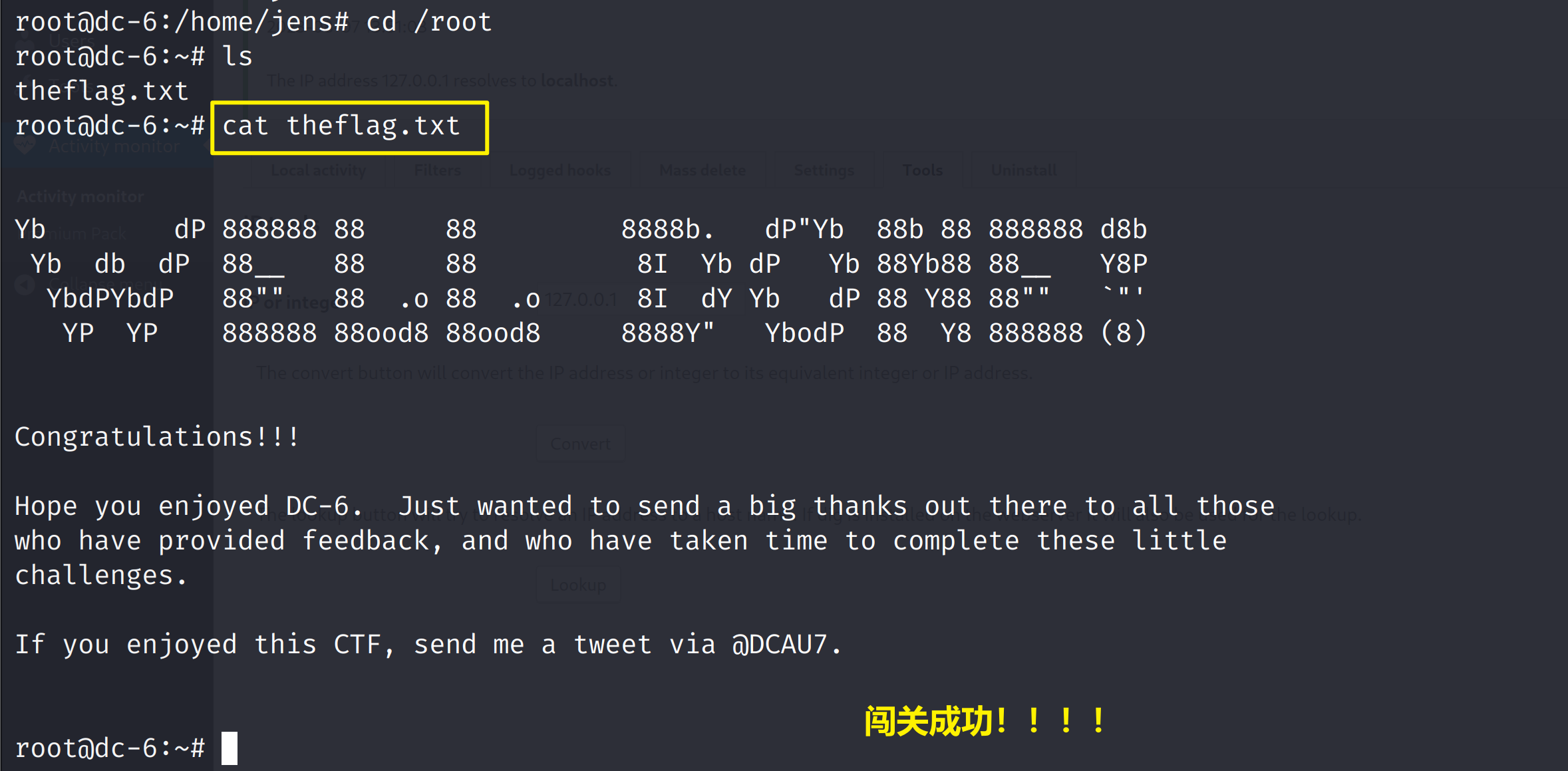
DC-6靶机
先去看看DC-6的官网描述,看看有没有给出提示信息 把这个线索信息先复制下来 cat /usr/share/wordlists/rockyou.txt | grep k01 > passwords.txt开始前先要吧 kali和DC-6靶机放在统一网段,都换成NAT模式 然后看一下DC-6的MAC地址 靶机的MAC地址00…...

SpringCloud入门Day01-服务注册与发现、服务通信、负载均衡与算法
SpringCloudNetflix入门 一、应用架构的演变 伴随互联网的发展,使用互联网的人群越来越多,软件应用的体量越来越大和复杂。而传统单体应用 可能不足以支撑大数据量以及发哦并发场景应用的框架也随之进行演变从最开始的单体应用架构到分布式(…...
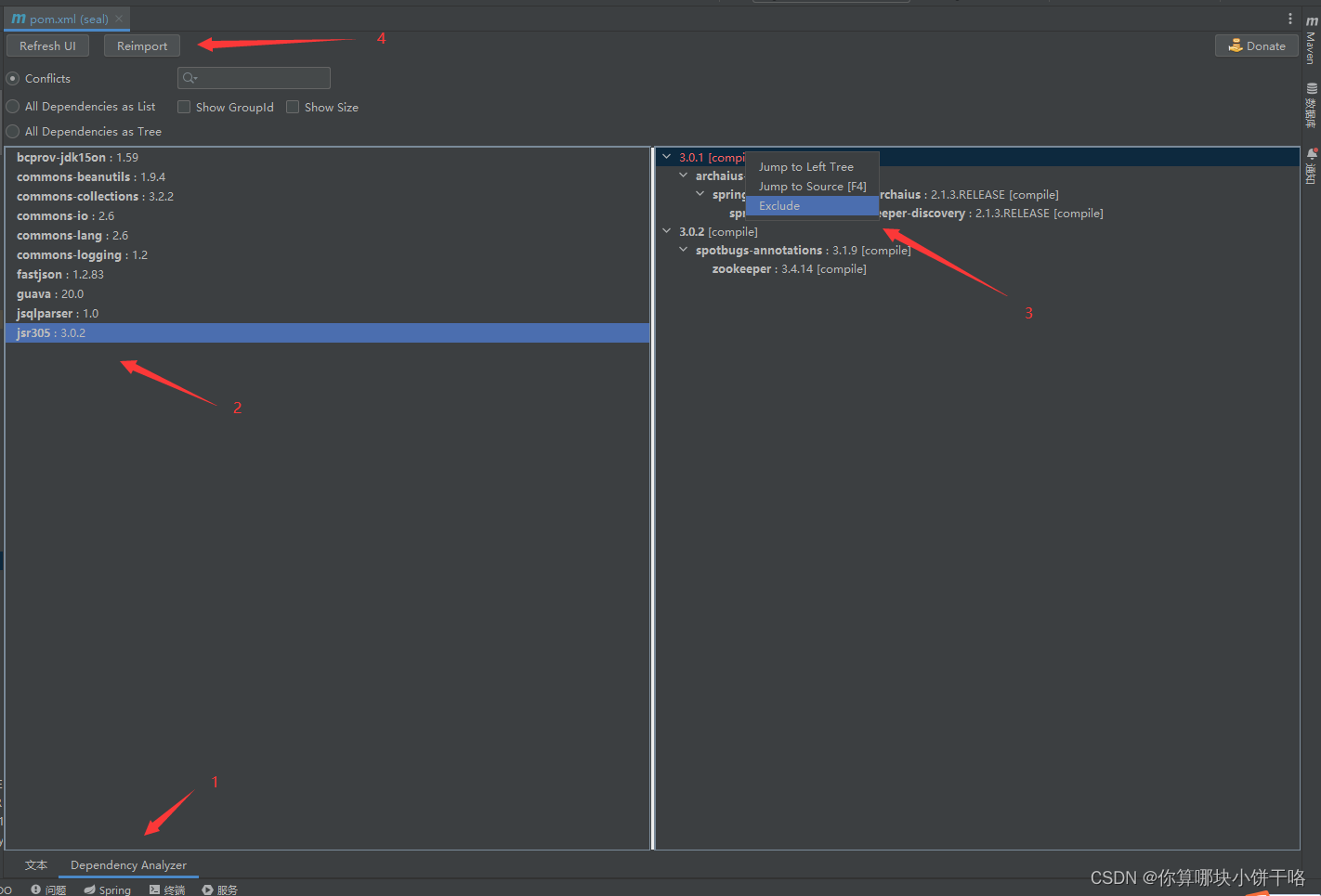
java-IDEA MAVEN查看依赖树,解决jar包重复和冲突
如果这里面的依赖关系有红线,就说明有包冲突,一般都是版本不一致,可以在idea里下一个插件Maven Helper,点击install并重启IDEA 打开pom.xml文件,在下方会出现Dependency Analyzer,选择它会出现重复依赖列表,选择对应的依赖,右键红…...
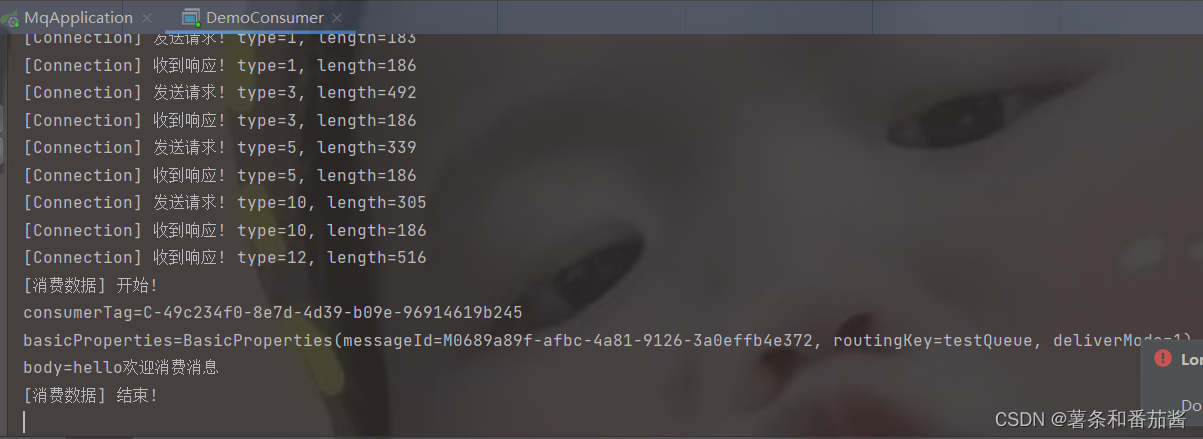
参考RabbitMQ实现一个消息队列
文章目录 前言小小消息管家1.项目介绍2. 需求分析2.1 API2.2 消息应答2.3 网络通信协议设计 3. 开发环境4. 项目结构介绍4.1 配置信息 5. 项目演示 前言 消息队列的本质就是阻塞队列,它的最大用途就是用来实现生产者消费者模型,从而实现解耦合以及削峰填…...

SpringBoot+JWT
一、maven坐标 <!-- JWT依赖 --><dependency><groupId>io.jsonwebtoken</groupId><artifactId>jjwt</artifactId><version>0.9.1</version></dependency><dependency><groupId>com.auth0</groupId>&…...

Cad二次开发EqualPoint
在 CAD 软件的二次开发中,Tolerance.Global.EqualPoint 是一个特定的属性或方法,用于表示全局的相等性公差值。这个属性或方法通常是由 CAD 软件的开发平台或 API 提供的,用于处理浮点数的相等性比较。 具体来说,Tolerance.Globa…...

20230806将ASF格式的视频转换为MP4
20230806将ASF格式的视频转换为MP4 2023/8/6 18:47 缘起,自考中山大学的《计算机网络》,考试《数据库系统原理》的时候找到视频,由于个人的原因,使用字幕更加有学习效率! 由于【重型】的PR2023占用资源较多,…...

【MySQL】——常用接口API即相关函数说明
目录 1、MySQL结构体的说明 1、MYSQL结构体 2.MYSQL_RES结构体 3. MYSQL_FIELD 2. 接口的使用步骤 3、mysql_init()——MYSQL对象初始化 4、mysql_real_connect()——数据库引擎建立连接 5. mysql_query()——查询数据库某表内容 6、mysql_real_query——执行SQL语句 …...
—— 实现请求封装)
ts + axios + useRequest (ahooks)—— 实现请求封装
现在越来越多的项目开始ts化,我们今天就一块学习一下,关于ts的请求封装。 首先要安装两个依赖: npm i axios -S npm i ahooks -S 引入: import { useRequest } from ahooks; import axios, { AxiosRequestConfig, AxiosRespo…...
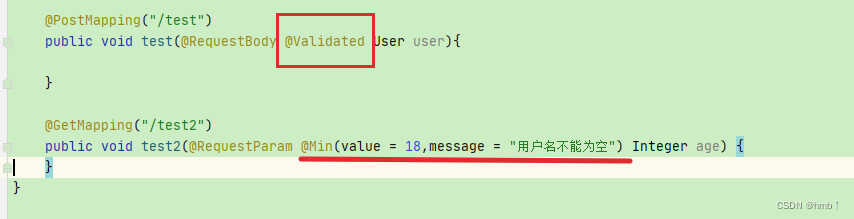
Springboot @Validated注解详细说明
在Spring Boot中,Validated注解用于验证请求参数。它可以应用在Controller类或方法上 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-validation</artifactId> </depen…...

STM32初学者,到底选标准库还是HAL库?
当初学者尝试学习STM32开发时,通常会面临一个关键的选择:是选择STM32的标准库,还是HAL库?这两个库各自有着优势与适用场景,本文将从多个角度分析,帮助初学者更好地选择适合自己的库。 在开始之前ÿ…...
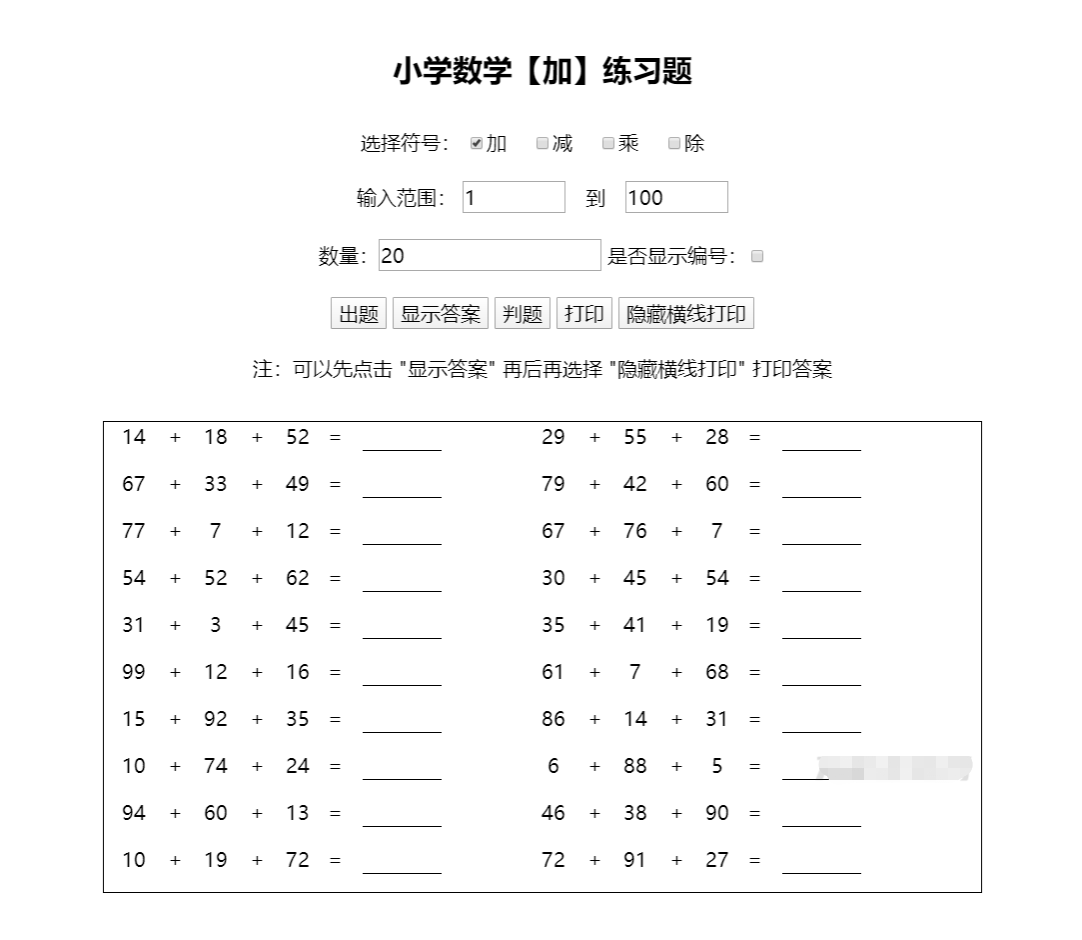
小学生作业随机加减乘除运算计算习题答案 html源码
小学生作业随机加减乘除运算计算习题答案 html源码 这道题目提供了多种选项,包括运算符和输入的运算数范围。题目数量也可以选择。如果你选择好了选项,就可以点击出题按钮进行练习。 为了方便,题目答案可以打印出来。但是,如果隐藏了横线,就会去除等号后面的下划线。推荐使用…...

nvm下载安装配置
一、作用 nvm是node版本管理的工具,具有管理、下载、切换node版本等能力。经常不同项目需要依赖不同版本的node,此时nvm就能有效的解决node版本切换的问题。 二、nvm下载安装配置 (1)安装包地址 https://github.com/coreybutl…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

GruntJS-前端自动化任务运行器从入门到实战
Grunt 完全指南:从入门到实战 一、Grunt 是什么? Grunt是一个基于 Node.js 的前端自动化任务运行器,主要用于自动化执行项目开发中重复性高的任务,例如文件压缩、代码编译、语法检查、单元测试、文件合并等。通过配置简洁的任务…...

永磁同步电机无速度算法--基于卡尔曼滤波器的滑模观测器
一、原理介绍 传统滑模观测器采用如下结构: 传统SMO中LPF会带来相位延迟和幅值衰减,并且需要额外的相位补偿。 采用扩展卡尔曼滤波器代替常用低通滤波器(LPF),可以去除高次谐波,并且不用相位补偿就可以获得一个误差较小的转子位…...

WPF八大法则:告别模态窗口卡顿
⚙️ 核心问题:阻塞式模态窗口的缺陷 原始代码中ShowDialog()会阻塞UI线程,导致后续逻辑无法执行: var result modalWindow.ShowDialog(); // 线程阻塞 ProcessResult(result); // 必须等待窗口关闭根本问题:…...

【无标题】湖北理元理律师事务所:债务优化中的生活保障与法律平衡之道
文/法律实务观察组 在债务重组领域,专业机构的核心价值不仅在于减轻债务数字,更在于帮助债务人在履行义务的同时维持基本生活尊严。湖北理元理律师事务所的服务实践表明,合法债务优化需同步实现三重平衡: 法律刚性(债…...

热门Chrome扩展程序存在明文传输风险,用户隐私安全受威胁
赛门铁克威胁猎手团队最新报告披露,数款拥有数百万活跃用户的Chrome扩展程序正在通过未加密的HTTP连接静默泄露用户敏感数据,严重威胁用户隐私安全。 知名扩展程序存在明文传输风险 尽管宣称提供安全浏览、数据分析或便捷界面等功能,但SEMR…...

Vue 3 + WebSocket 实战:公司通知实时推送功能详解
📢 Vue 3 WebSocket 实战:公司通知实时推送功能详解 📌 收藏 点赞 关注,项目中要用到推送功能时就不怕找不到了! 实时通知是企业系统中常见的功能,比如:管理员发布通知后,所有用户…...

基于开源AI智能名片链动2 + 1模式S2B2C商城小程序的沉浸式体验营销研究
摘要:在消费市场竞争日益激烈的当下,传统体验营销方式存在诸多局限。本文聚焦开源AI智能名片链动2 1模式S2B2C商城小程序,探讨其在沉浸式体验营销中的应用。通过对比传统品鉴、工厂参观等初级体验方式,分析沉浸式体验的优势与价值…...
