dfs之卒的遍历
题面
题目描述
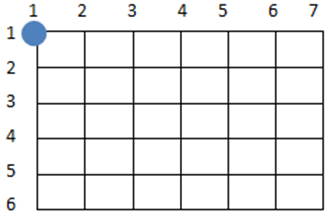
在一张n×m 的棋盘上(如 6 行 7 列)的最左上角(1,1) 的位置有一个卒。该卒只能向下或者向右走,且卒采取的策略是先向下,下边走到头就向右,请问从(1,1) 点走到 (n,m) 点可以怎样走,输出这些走法。
输入
两个整数n,m 代表棋盘大小(3≤n≤8,3≤m≤8)
输出
卒的行走路线。
样例
输入
复制
3 3输出
复制
1:1,1->2,1->3,1->3,2->3,3 2:1,1->2,1->2,2->3,2->3,3 3:1,1->2,1->2,2->2,3->3,3 4:1,1->1,2->2,2->3,2->3,3 5:1,1->1,2->2,2->2,3->3,3 6:1,1->1,2->1,3->2,3->3,3链接
先深搜到终点输出在return回去
解法一:函数包含三个参数X,Y,K
#include <bits/stdc++.h>
using namespace std;
int n , m , c = 0 , r[20][3];
int fx[3] = {0 , 1 , 0} , fy[3] = {0 , 0 , 1};
void print(int k){c++;printf("%d:" , c);for ( int i = 1 ; i < k ; i++ )printf("%d,%d->" , r[i][1] , r[i][2]);printf("%d,%d" , n , m);printf("\n");
}
void dfs( int x , int y , int k){r[k][1] = x;r[k][2] = y;if(x == n && y == m){print(k);return;}int tx , ty;for ( int i = 1 ; i <= 2 ; i++ ){tx = x + fx[i];ty = y + fy[i];if(tx >= 1 && tx <= n && ty >= 1 && ty <= m )dfs(tx , ty , k+1);}
}
int main(){scanf("%d%d" , &n , &m);dfs(1,1,1);return 0;
}解法二:直接用r数组里存的元素
#include <bits/stdc++.h>
using namespace std;
int n , m , c = 0 , r[20][3];
int fx[3] = {0 , 1 , 0} , fy[3] = {0 , 0 , 1};
void print(int k){c++;printf("%d:" , c);for ( int i = 1 ; i < k ; i++ )printf("%d,%d->" , r[i][1] , r[i][2]);printf("%d,%d" , n , m);printf("\n");
}
void dfs(int k){int tx , ty;for ( int i = 1 ; i <= 2 ; i++ ){tx = r[k-1][1] + fx[i];ty = r[k-1][2] + fy[i];if(tx >= 1 && tx <= n && ty >= 1 && ty <= m ){r[k][1] = tx;r[k][2] = ty;if(tx == n && ty == m) print(k);else dfs(k+1);}}
}
int main(){scanf("%d%d" , &n , &m);r[1][1] = 1;r[1][2] = 1;dfs(2);return 0;
}相关文章:
dfs之卒的遍历
题面 题目描述 在一张nm 的棋盘上(如 6 行 7 列)的最左上角(1,1) 的位置有一个卒。该卒只能向下或者向右走,且卒采取的策略是先向下,下边走到头就向右,请问从(1,1) 点走到 (n,m) 点可以怎样走,输出这些走法…...

Springboot整合activiti5,达梦数据库,mybatis中间件
Springboot整合activiti5,达梦数据库,mybatis中间件 问题现象解决方案 问题现象 由于工作流引擎不支持达梦数据库以及国产中间件,所以我们引入的时候会报错,这个时候就需要去改造代码和配置文件。各种文档和资料查找一天…...
使用Python + Flask搭建web服务
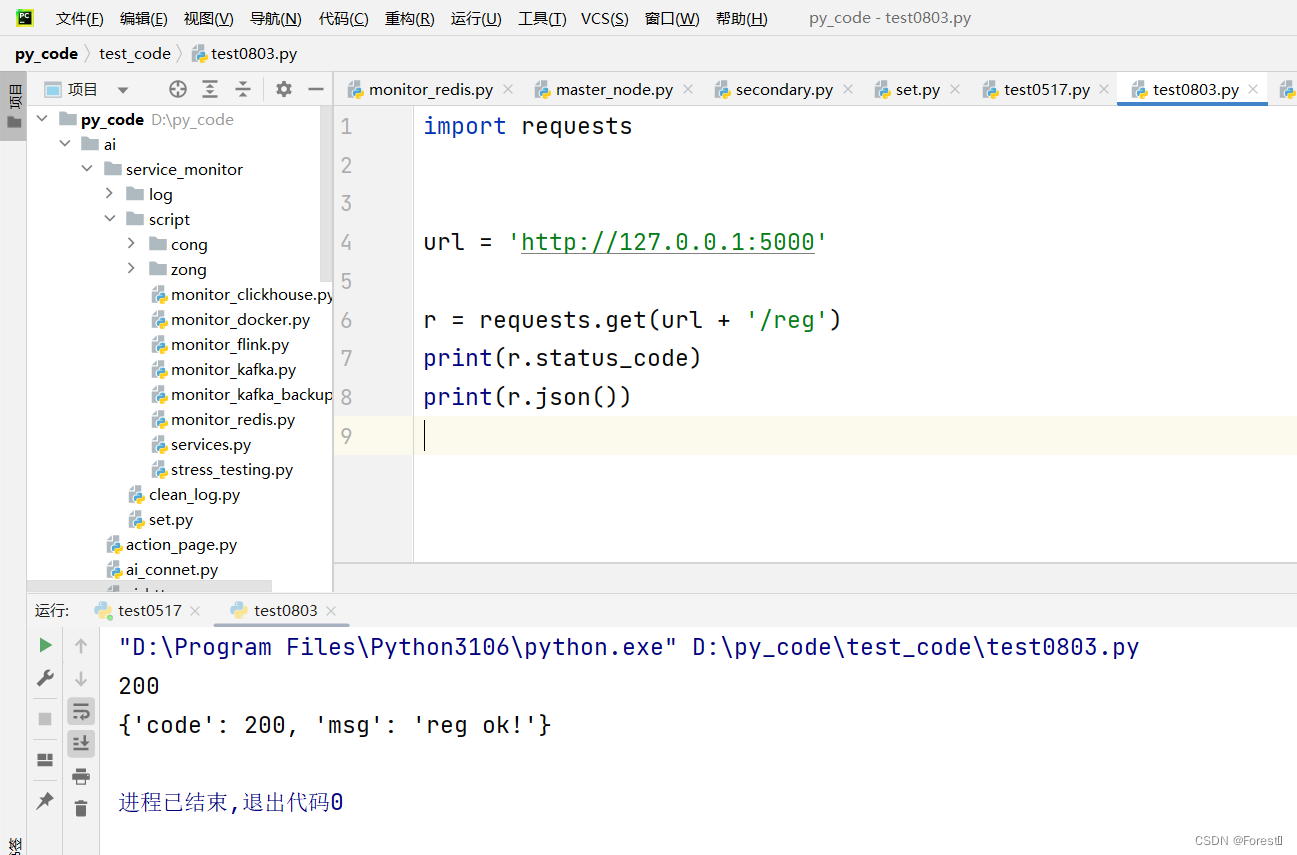
示例脚本 from flask import Flask# 获取一个实例对象 app Flask(__name__)# 1、注册 app.route(/reg, methods[get]) def reg():return {code: 200,msg: reg ok!}# 2、登录 app.route(/login, methods[get]) def login():return login ok!if __name__ __main__:…...

Winform 打开文件夹、文件、拖拽上传
参考原文:https://blog.csdn.net/u012543266/article/details/21834073 1、打开文件 private void button1_Click(object sender, EventArgs e){OpenFileDialog dialog new OpenFileDialog();dialog.Multiselect true;//该值确定是否可以选择多个文件dialog.Titl…...
热评国内AI四小龙:此一时彼一时,彼此彼此
引言:阿里“清仓”全部持股 商汤科技表示“没啥事” 【科技明说 | 热点关注】 作为国内AI领域的知名科技上市公司,商汤科技SenseTime的一举一动都牵动着业内人士的心。 然而,商汤科技的财报表现没有出奇制胜,却让不…...

[国产MCU]-BL602开发实例-GPIO控制
GPIO与控制 文章目录 GPIO与控制1、GPIO介绍2、GPIO管理相关API介绍3、硬件准备4、软件准备5、代码实现3.1 GPIO输出3.2 GPIO输入3.3 GPIO中断BL602的GLB(Global Register)是芯片通用全局设定模块,主要包含了时钟管理、复位管理、总线管理、内存管理以及GPIO管理等功能。 本文…...

Firefox 配置 Burp_proxy 和 证书
安装代理拓展 安装拓展: chrome : switchomega firefox : foxyproxy 创建代理 : 127.0.0.1:8080 安装burp证书 先开启burp,然后切换到 burp 的代理访问 https://burp/ 下载证书打开firefox设置 - 搜索”证书“ -…...
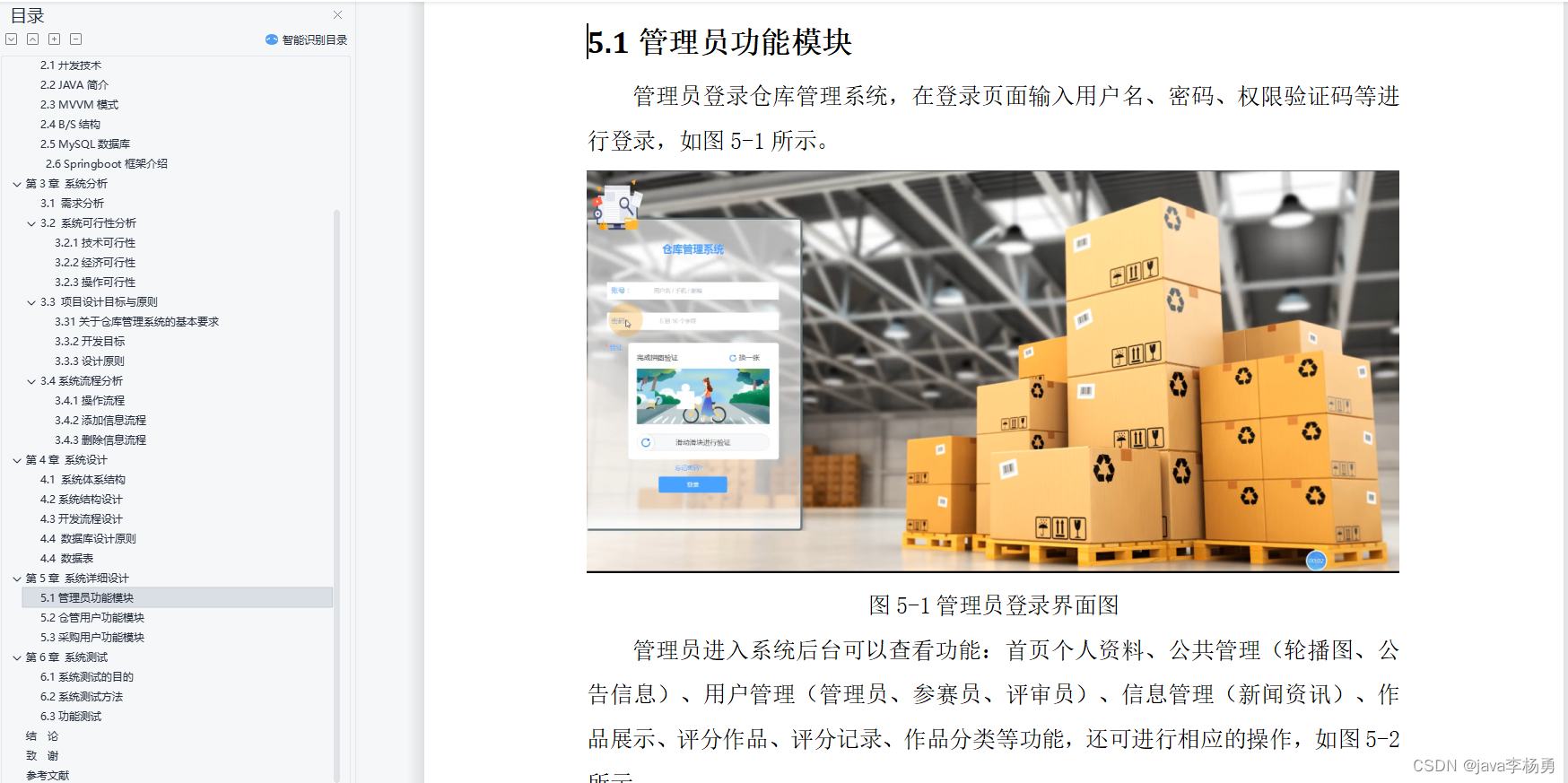
基于Java+SpringBoot+Vue前后端分离仓库管理系统详细设计和实现
博主介绍:✌全网粉丝30W,csdn特邀作者、博客专家、CSDN新星计划导师、Java领域优质创作者,博客之星、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 🍅文末获取源码联系🍅 👇🏻 精彩专…...

PyTorch Lightning教程七:可视化
本节指导如何利用Lightning进行可视化和监控模型 为何需要跟踪参数 在模型开发中,我们跟踪感兴趣的值,例如validation_loss,以可视化模型的学习过程。模型开发就像驾驶一辆没有窗户的汽车,图表和日志提供了窗口,让我们…...

后端开发2.mongdb的集成
使用docker安装 安装 拉取镜像 docker pull mongo:4.4.14-focal 创建容器 docker run -itd --name mongo -p 8036:27017 mongo:4.4.14-focal --auth 配置管理员 进入容器 docker exec -it mongo bash 进入终端 mongo 进入admin数据库 use admin 创建管理员账户 db.c…...

Unity面板究极优化
首先对于大项目来说UI首选一定的UGUI,目前没有啥可选的余地。多一点都是对性能的负担,UGUI底层基于多线程技术,可以有效分担压力,对于一些不是那么重的面板几乎无感。 无论其他面板只是在此基础上修改的,但每多一层&am…...

C# App.config和Web.config加密
步骤1:创建加密命令 使用ASP.NET提供的命令工具aspnet_regiis来创建加密命令。 1、打开控制台窗口,在命令行中输入以下命令: cd C:\Windows\Microsoft.NET\Framework\v4.xxxxx aspnet_regiis.exe -pef connectionStrings "C:\MyAppFo…...
(Python3))
力扣:50. Pow(x, n)(Python3)
题目: 实现 pow(x, n) ,即计算 x 的整数 n 次幂函数(即,xn )。 来源:力扣(LeetCode) 链接:力扣 示例: 示例 1: 输入:x 2.00000, n 1…...
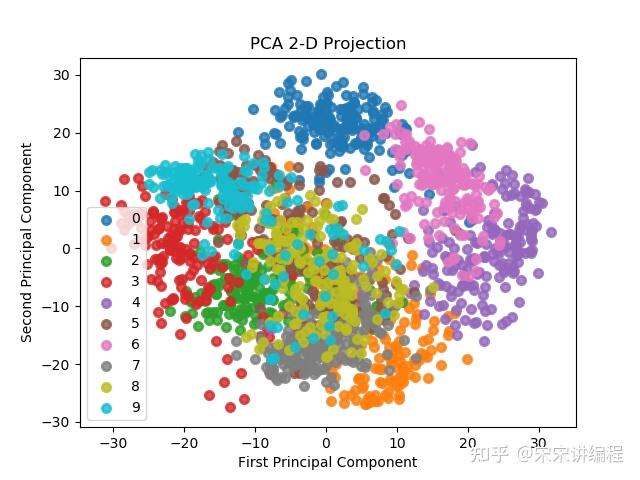
scikit-plot 使用笔记
scikit-plot是基于sklearn和Matplotlib的库,主要的功能是对训练好的模型进行可视化。 安装: pip install scikit-plot 功能1:评估指标可视化 scikitplot.metrics.plot_confusion_matrix快速展示模型预测结果和标签计算得到的混淆矩阵。 im…...

2024考研408-计算机网络 第五章-传输层学习笔记
文章目录 前言一、传输层提供的服务1.1、传输层的功能1.2、传输层的两个协议(TCP、UDP)1.3、传输层的寻址与端口(常见端口介绍) 二、UDP协议2.1、认识UDP功能和特点2.2、UDP首部格式2.3、UDP伪首部字段分析2.4、伪首部校验UDP用户…...

【JS】一道解构面试题
文章目录 [TOC] 一道解构面试题题目运行结果 原理概念数组迭代器 答案答案(1)、在对象中添加一个数组迭代器1.使用临时数组添加迭代器2. 对象值输出结果3.使用Object.values(this);拿到对象的值 答案(2)、在对象原型上添加数组迭代器1.按步骤实现数组迭代器2. 简化步骤 答案(3)…...

24v转3.3v输出3A用什么芯片
问:客户需要一个能够将24V输入电压转换为3.3V输出电压,并且能够提供1-3A的电流输出的芯片。还希望它能够内置MOS管。有什么推荐的型号吗?(vin24v、5v,vout3.3v,Io1-3A) 答:推荐使用…...
在Linux中安装lrzsz(yum命令使用)
在Linux中安装lrzsz(yum命令使用) 操作步骤: 1、搜索lrzsz安装包,命令为yum list lrzsz 2、使用yum命令在线安装,命令为yum install lrzsz.x86_64 注意事项: Yum(全称为 Yellow dog Updater, Modified)是一个在Fedor…...
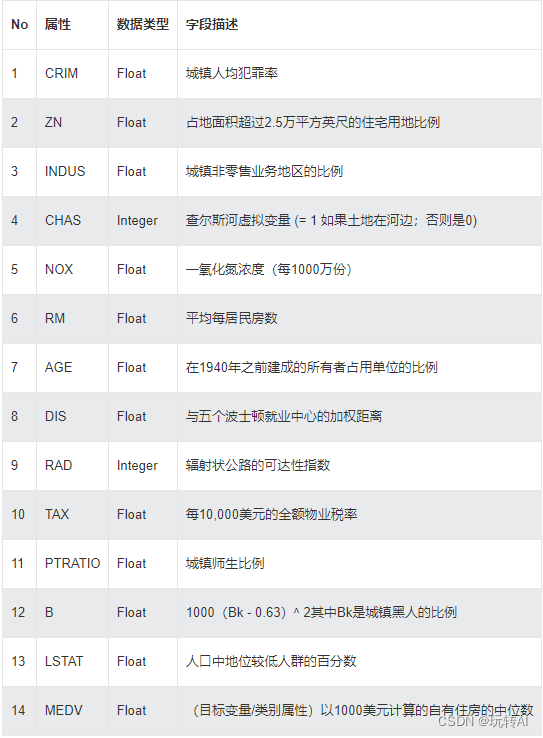
机器学习基础08-回归算法矩阵分析(基于波士顿房价(Boston House Price)数据集)
回归算法通常涉及到使用矩阵来表示数据和模型参数。线性回归是最常见的回归算法之一,它可以用矩阵形式来表示。 考虑一个简单的线性回归模型: y m x b y mx b ymxb,其中 y y y 是因变量, x x x 是自变量, m m m 是…...

[英语单词] password, passphrase, passport.... paraphrase
password 是密码,大多可能就是一个单词的量,10多个字母,或者更少;而且就是一个单词; 后来发现密码这么设置不安全,怎么办? 就出现了passphrase,使用词组的组合来做为密码,…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...

MySQL 部分重点知识篇
一、数据库对象 1. 主键 定义 :主键是用于唯一标识表中每一行记录的字段或字段组合。它具有唯一性和非空性特点。 作用 :确保数据的完整性,便于数据的查询和管理。 示例 :在学生信息表中,学号可以作为主键ÿ…...

(一)单例模式
一、前言 单例模式属于六大创建型模式,即在软件设计过程中,主要关注创建对象的结果,并不关心创建对象的过程及细节。创建型设计模式将类对象的实例化过程进行抽象化接口设计,从而隐藏了类对象的实例是如何被创建的,封装了软件系统使用的具体对象类型。 六大创建型模式包括…...
