AtCoder Regular Contest 126 D题题解
思路
首先我们看看假设选中 mmm 个数后的答案。
我们首先现将 mmm 个数移动到一起,在将他们重新排序。
我们知道,mmm 个数移在一起时,当位于中间的那个数不动时交换次数最少,于是可以列出式子(cic_ici 是点 iii 的位置):
∑i=1m∣cmid+mid−ci+i∣\sum_{i = 1}^m |c_{mid} + mid - c_i + i| i=1∑m∣cmid+mid−ci+i∣
我们可以将上面的式子改成如下形式:
−2m∗mid+m%2∗cmid+∑i=1mci−1i<=mid-\dfrac{2}{m}*mid + m \% 2 * c_{mid} + \sum_{i = 1}^m c_i^{-1^{i <=mid}} −m2∗mid+m%2∗cmid+i=1∑mci−1i<=mid
此时我们就可以用壮压DP来做了。
我们首先枚举每个数,在枚举选上这个数后的情况,在DP的过程中计算出下面的式子的求和公式里面的值,前面的为常数,并且在加上逆序对个数就可以了。
代码
#include <bits/stdc++.h>
using namespace std;
int n, m, mid, a[205], f[205][1 << 18], INF = 1e9;
int solve(int state, int i) {int sum = 0, t = 0, t1 = 0;//t是目前选了多少个数,t1选了的树中比这个数要小的数。for (int j = 0; j < m; j++) {if (state & (1 << j))t++;if (a[i] - 1 == j)t1 = t;}return i * (t <= mid ? -1 : 1) + i * (m & 1) * (mid == t) + (t - t1);//此时的i就是c值,于是我们把他带进去式子就可以了。
}
int main() {scanf("%d%d", &n, &m), mid = (m + 1) / 2;for (int i = 1; i <= n; i++) scanf("%d", &a[i]);memset(f, 36, sizeof(f));for (int i = 0; i <= n; i++) f[i][0] = 0;for (int i = 1; i <= n; i++)for (int j = 0; j < 1 << m; j++)f[i][j] = min(j & (1 << (a[i] - 1)) ? f[i - 1][j ^ (1 << (a[i] - 1))] + solve(j, i) : INF, f[i - 1][j]);printf("%d", f[n][(1 << m) - 1] - m / 2 * mid);return 0;
}
相关文章:

AtCoder Regular Contest 126 D题题解
思路 首先我们看看假设选中 mmm 个数后的答案。 我们首先现将 mmm 个数移动到一起,在将他们重新排序。 我们知道,mmm 个数移在一起时,当位于中间的那个数不动时交换次数最少,于是可以列出式子(cic_ici 是点 iii 的…...

Android R WiFi热点流程浅析
Android R WiFi热点流程浅析 Android上的WiFi SoftAp功能是用户常用的功能之一,它能让我们分享手机的网络给其他设备使用。 那Android系统是如何实现SoftAp的呢,这里在FWK层面做一个简要的流程分析,供自己记录和大家参考。 以Android R版本为…...
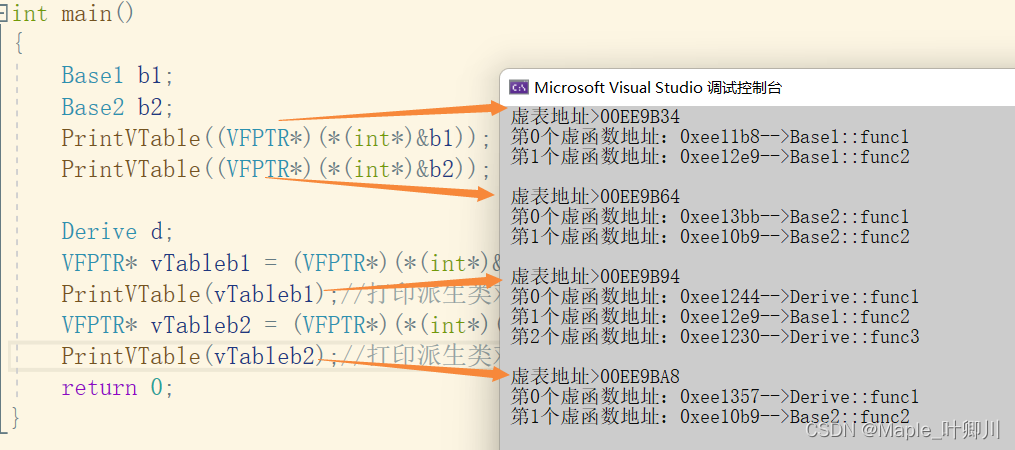
【C++进阶】二、多态详解(总)
目录 一、多态的概念 二、多态的定义及实现 2.1 多态的构成条件 2.2 虚函数 2.3 虚函数的重写 2.4 虚函数重写的两个例外 2.4.1 协变 2.4.2 析构函数的重写 2.5 C11 override 和 final 2.5.1 final 2.5.2 override 2.6 重载、覆盖(重写)、隐藏(重定义)的对比 三、…...
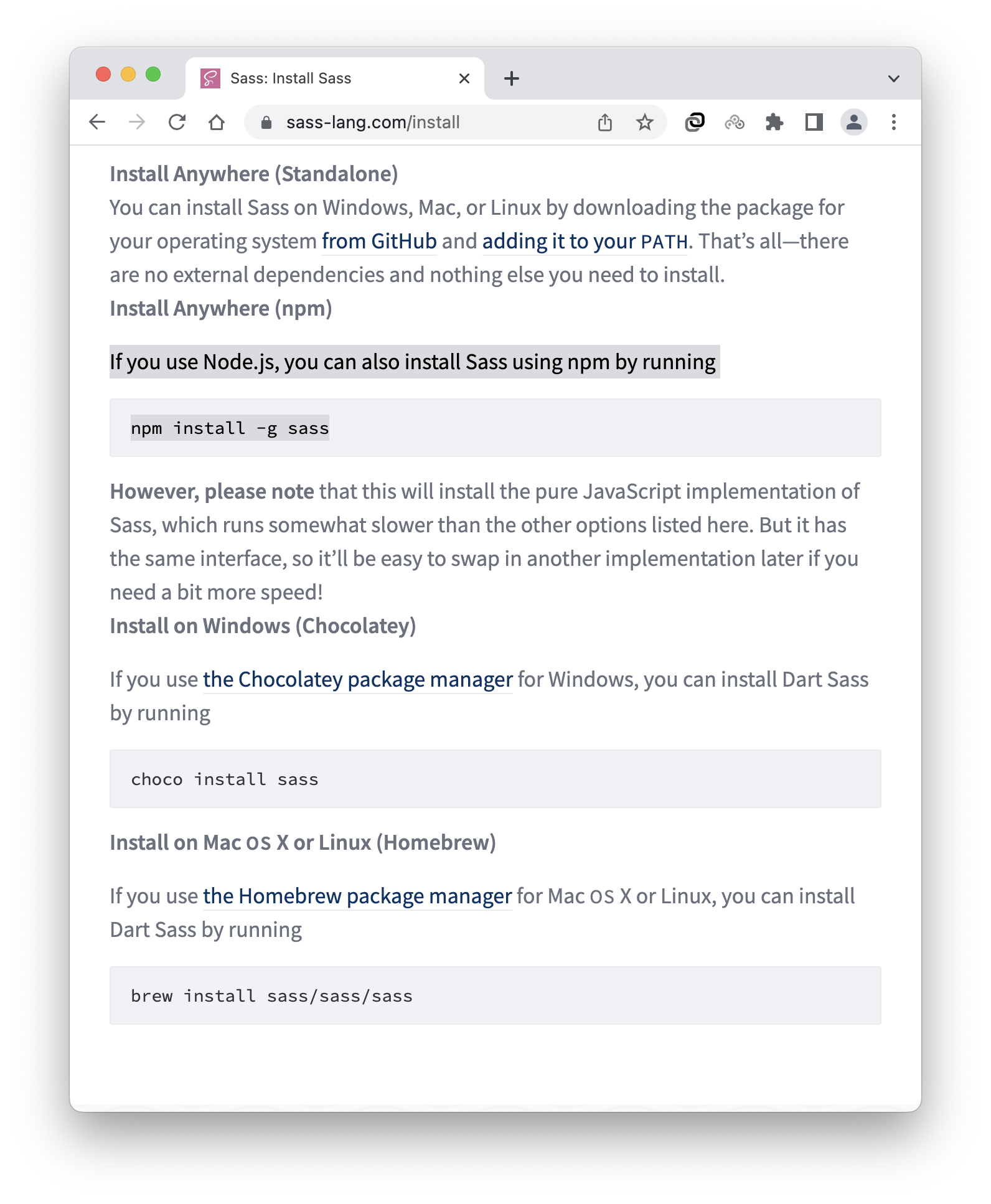
node-sass@4.14.1 包含风险, 如何升级依赖至 dart-sass
文章目录需求我上网都查到了哪些信息在 github 看到了 node-sass 依赖的最新版本的列表:关于方案2的失败不同版本的 nodejs 和 node-sass依赖的**适配关系**从何得知替代方案——dart-sass如何安装 dart sass?需求 在做一个基于Node、React的前端项目&a…...
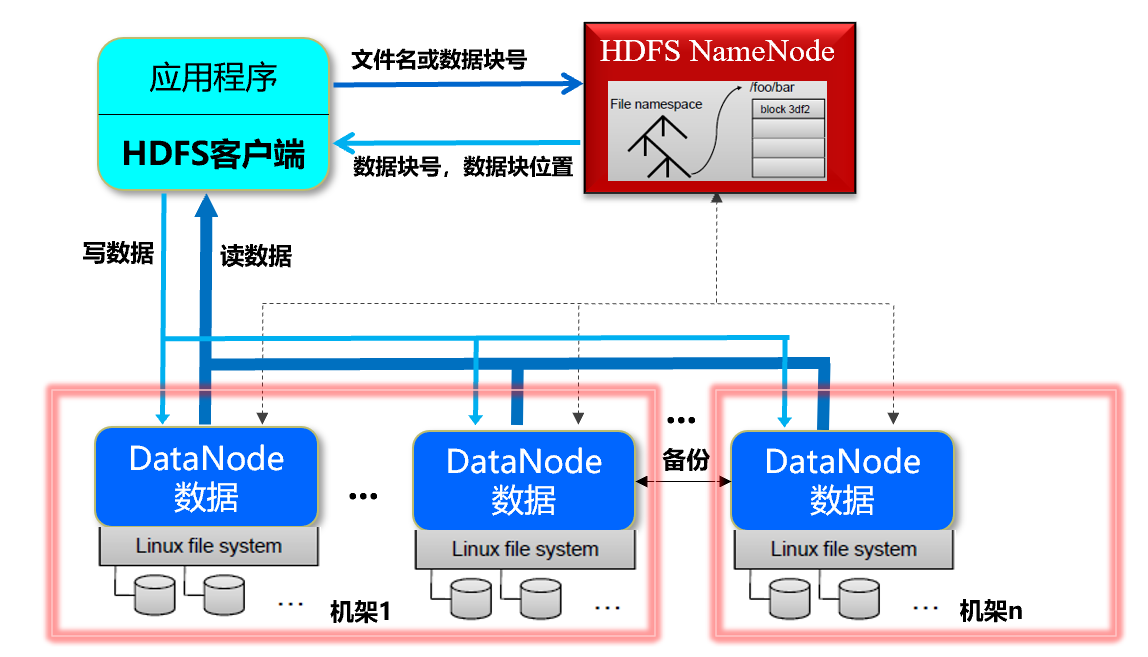
DataWhale 大数据处理技术组队学习task2
三、Hadoop分布式文件系统 1. 产生背景 数据量越来越大,一台独立的计算机已经无法存储所有的数据---->将大规模的数据存储到成百上千的计算机中------为了解决数据管理以及维护极其繁琐与低效------>分布式文件系统 分布式文件系统是管理网络中跨多台计算机…...

一文读懂select、poll、epoll的用法
select,poll,epoll都是IO多路复用的机制。I/O多路复用就通过一种机制,可以监视多个描述符,一旦某个描述符就绪(一般是读就绪或者写就绪),能够通知程序进行相应的读写操作。但select,…...

《C陷阱与缺陷》----词法“陷阱”
导言: 由于一个程序错误可以从不同层面采用不同方式进行考察,而根据程序错误与考察程序的方式之间的相关性,可以将程序错误进行划分为各种陷阱与缺陷: ①.词法“陷阱” ②.语法“陷阱” ③.语义“陷阱” ④.连接问题 ⑤.库函数问…...

千锋教育+计算机四级网络-计算机网络学习-04
UDP概述 UDP协议 面向无连接的用户数据报协议,在传输数据前不需要先建立连接;目地主机的运输层收到UDP报文后,不需要给出任何确认 UDP特点 相比TCP速度稍快些简单的请求/应答应用程序可以使用UDP对于海量数据传输不应该使用UDP广播和多播应用…...

蓝桥杯算法训练合集十四 1.P08052.P07053.同余方程4.P08015.ascii应用
目录 1.P0805 2.P0705 3.同余方程 4.P0801 5.ascii应用 1.P0805 问题描述 当两个比较大的整数相乘时,可能会出现数据溢出的情形。为避免溢出,可以采用字符串的方法来实现两个大数之间的乘法。具体来说,首先以字符串的形式输入两个整数&…...
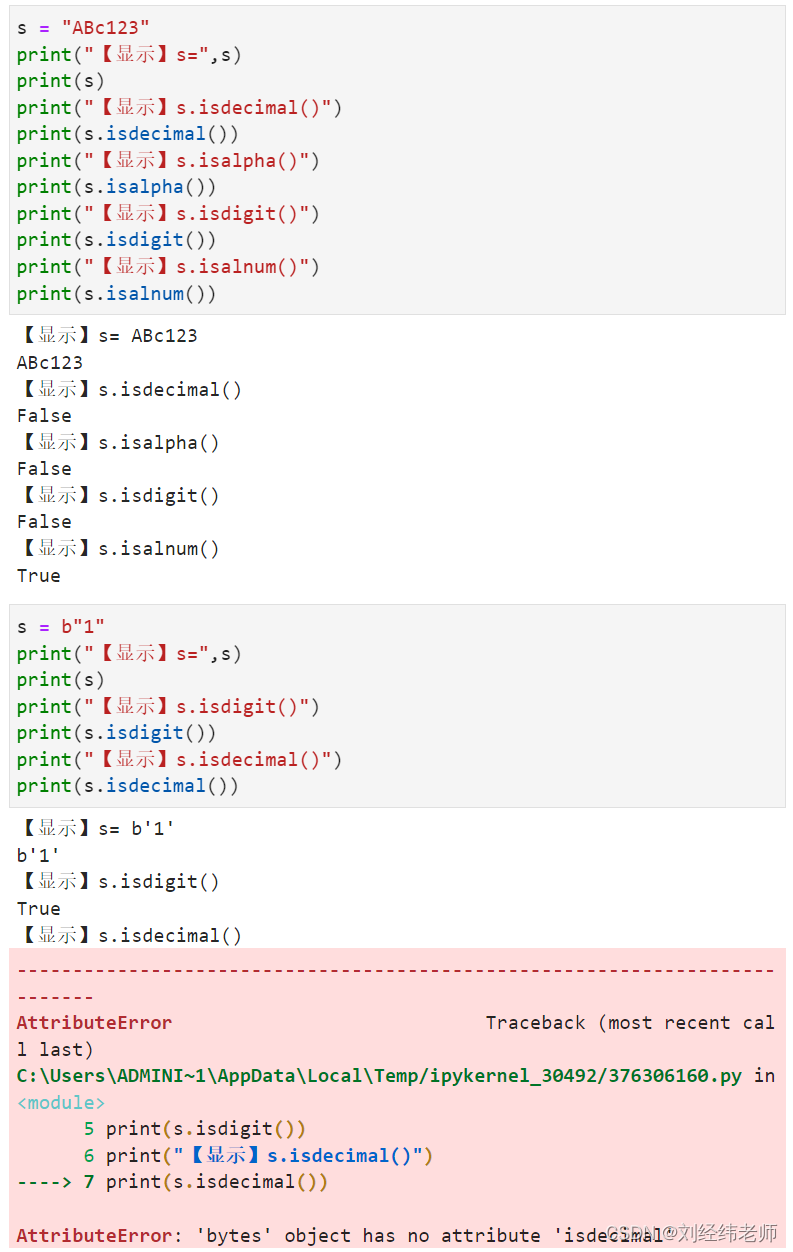
判断字符串中的字符的类型isdecimal();isalpha();isdigit();isalnum()
【小白从小学Python、C、Java】 【计算机等级考试500强双证书】 【Python-数据分析】 判断字符串中的字符的类型 isdecimal();isalpha();isdigit();isalnum() [太阳]选择题 对于代码中isdecimal()和isalnum()输出的结果是? s "ABc123&…...
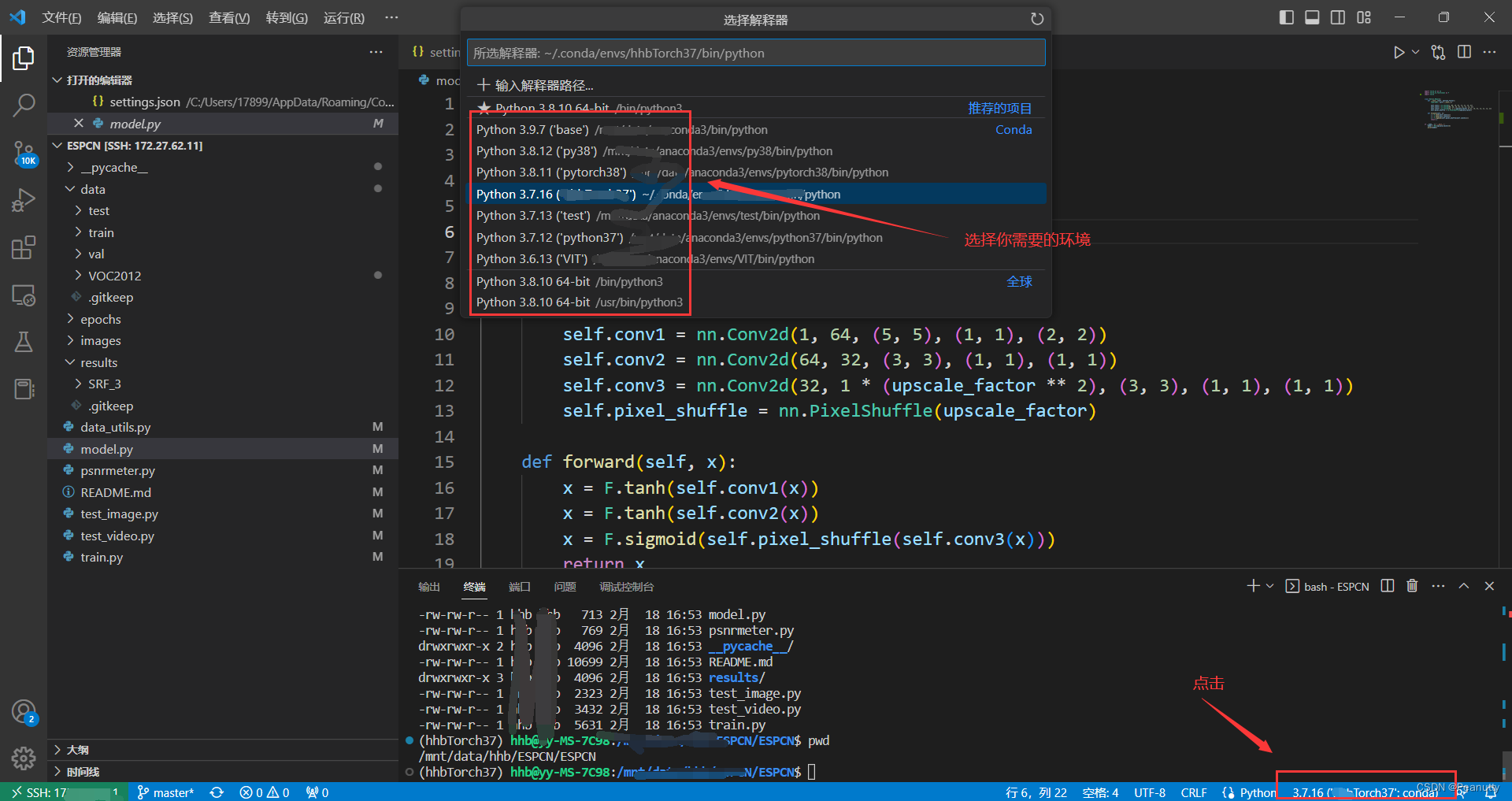
VSCode远程调试Linux代码,python解释器配置
安装插件并配置 安装后找到插件图标,点击 点击SSH上的 号 在弹出框中输入命令:ssh usernameip -p port username: 远程服务器的用户名 ip: 远程ip port:端口号,没有可以不用 输入完毕后点击enter 选择ssh配置文件保存…...

03:入门篇 - CTK Plugin Framework 基本原理
作者: 一去、二三里 个人微信号: iwaleon 微信公众号: 高效程序员 CTK Plugin Framework 技术是面向 C++ 的动态模型系统。该系统允许插件之间的松散耦合,并且提供了设计良好的方式来进行功能和数据的交互。此外,它没有预先对插件施加限制,这样就可以很容易地将插件的相关…...
)
面试攻略,Java 基础面试 100 问(九)
数组有没有 length()方法?String 有没有 length()方法? 数组没有 length()方法,有 length 的属性。String 有 length()方法。JavaScript 中,获得字符串的长度是通过 length 属性得到的,这一点容易和 Java混淆。 在 Java 中&…...

JavaScript 代码不嵌套主义
文章目录前言一、何为嵌套代码二、避免嵌套1.提炼抽取2.反转排列总结前言 看过不少过度嵌套的代码, 我真正意识到问题的严重性是刚入职那会, 我在一个老项目里看到了40个连续的else if, 套了6层的if, for和forEach, 因为我们并没有做什么限制代码嵌套的提前约定. 呃, 那之后认…...

使用默认参数的4大要点
概述 默认参数是C中新增的特性。在C中,可以为函数的参数指定默认值。调用函数时,如果没有指定实参,则自动使用默认参数。默认参数的基本语法这里就不作介绍了,下面重点介绍使用默认参数的一些知识要点。 基本规则 1、当函数中某个…...
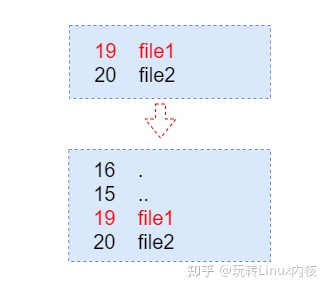
Linux文件系统中的硬链接及常见面试题
如果能对inode的概念有所了解,对理解本文会有所帮助。如果对inode的概念不太清楚也没有关系,我们会捎带介绍一下。在文件系统的实现层面,我们可以认为包含两个组件:一个是包含数据块的池子,池子中的数据块是等大小的&a…...

opencv-StereoBM算法
原理解释目前立体匹配算法是计算机视觉中的一个难点和热点,算法很多,但是一般的步骤是:A、匹配代价计算匹配代价计算是整个立体匹配算法的基础,实际是对不同视差下进行灰度相似性测量。常见的方法有灰度差的平方SD(squ…...

图像分类竞赛进阶技能:OpenAI-CLIP使用范例
OpenAI-CLIP 官方介绍 尽管深度学习已经彻底改变了计算机视觉,但目前的方法存在几个主要问题:典型的视觉数据集是劳动密集型的,创建成本高,同时只教授一组狭窄的视觉概念;标准视觉模型擅长于一项任务且仅擅长于一项任务,并且需要大…...
Metasploit框架基础(一)
文章目录前言一、基础认知二、批量POC/EXP的构想三、poc检测框架的简单实现四、xray五、Meatsploit框架参考前言 Metasploit 一款渗透测试框架漏洞利用的集合与构建和定制满足你的需求的基础漏洞利用和验证的工具 这几个说法都是百度或者官方文档中出现的手法,说…...
——标签转换与数据加载)
pytorch零基础实现语义分割项目(二)——标签转换与数据加载
数据转换与加载项目列表前言标签转换RGB标签到类别标签映射RGB标签转换成类别标签数据数据加载随机裁剪数据加载项目列表 语义分割项目(一)——数据概况及预处理 语义分割项目(二)——标签转换与数据加载 语义分割项目&#x…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

LabVIEW双光子成像系统技术
双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制,展现出显著的技术优势: 深层组织穿透能力:适用于活体组织深度成像 高分辨率观测性能:满足微观结构的精细研究需求 低光毒性特点:减少对样本的损伤…...

Vite中定义@软链接
在webpack中可以直接通过符号表示src路径,但是vite中默认不可以。 如何实现: vite中提供了resolve.alias:通过别名在指向一个具体的路径 在vite.config.js中 import { join } from pathexport default defineConfig({plugins: [vue()],//…...

Chromium 136 编译指南 Windows篇:depot_tools 配置与源码获取(二)
引言 工欲善其事,必先利其器。在完成了 Visual Studio 2022 和 Windows SDK 的安装后,我们即将接触到 Chromium 开发生态中最核心的工具——depot_tools。这个由 Google 精心打造的工具集,就像是连接开发者与 Chromium 庞大代码库的智能桥梁…...

如何配置一个sql server使得其它用户可以通过excel odbc获取数据
要让其他用户通过 Excel 使用 ODBC 连接到 SQL Server 获取数据,你需要完成以下配置步骤: ✅ 一、在 SQL Server 端配置(服务器设置) 1. 启用 TCP/IP 协议 打开 “SQL Server 配置管理器”。导航到:SQL Server 网络配…...
