第三章 图论 No.6负环之01分数规划与特殊建图方式
文章目录
- 裸题:904. 虫洞
- 01分数规划:361. 观光奶牛
- 特殊建图与01分数规划+trick:1165. 单词环
裸题:904. 虫洞
904. 虫洞 - AcWing题库

// 虫洞是负权且单向边,道路是正权且双向边,题目较裸,判断有无负环即可
#include <iostream>
#include <cstring>
using namespace std;const int N = 510, M = 6010;
int h[N], e[M], ne[M], w[M], idx;
int n, m, k;
int dis[N], cnt[N];
int q[N];
bool st[N];void add(int x, int y, int d)
{e[idx] = y, ne[idx] = h[x], w[idx] = d, h[x] = idx ++ ;
}bool spfa()
{int tt = 0, hh = 0;memset(cnt, 0, sizeof(cnt));memset(dis, 0, sizeof(dis));memset(st, 0, sizeof(st));for (int i = 1; i <= n; ++ i ) st[i] = true, q[tt ++ ] = i;while (hh != tt){int x = q[hh ++ ];if (hh == N) hh = 0;st[x] = false;for (int i = h[x]; i != -1; i = ne[i]){int y = e[i];if (dis[y] > dis[x] + w[i]){cnt[y] = cnt[x] + 1;if (cnt[y] >= n) return true;dis[y] = dis[x] + w[i];if (!st[y]) {st[y] = true;q[tt ++ ] = y;if (tt == N) tt = 0;}}}}return false;
}int main()
{int T;scanf("%d", &T);while (T -- ){memset(h, -1, sizeof(h));idx = 0;scanf("%d%d%d", &n, &m, &k);int x, y, d;for (int i = 0; i < m; ++ i ){scanf("%d%d%d", &x, &y, &d);add(x, y, d), add(y, x, d);}for (int i = 0; i < k; ++ i ){scanf("%d%d%d", &x, &y, &d);add(x, y, -d);}if (spfa()) puts("YES");else puts("NO");}return 0;
}
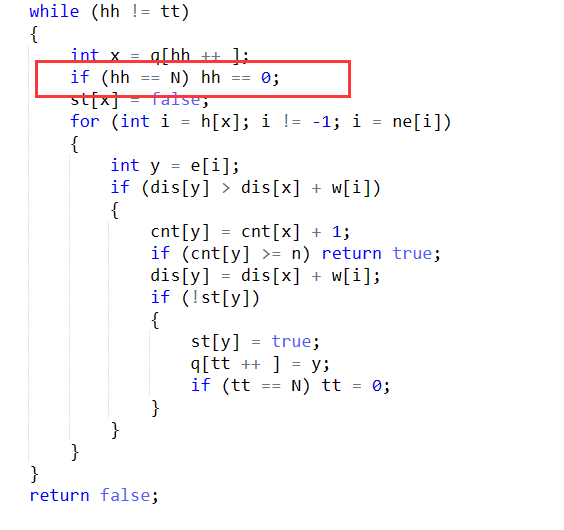
这个==真的服,调半天,还有,邻接表的大小又设置错了
01分数规划:361. 观光奶牛
361. 观光奶牛 - AcWing题库
在图论问题中,所有形如:某个部分之和除以某个部分之和最大的问题,被称为01分数规划,通常使用二分解决这类问题
根据题意,这道题的答案范围在 ( 0 , 1000 ] (0, 1000] (0,1000]中,我们需要二分这个区间找到答案
若点权之和/边权之和大于等于mid,则说明答案在 [ m i d , r ] [mid, r] [mid,r]之间
反之,点权之和/边权小于mid,则说明答案在 [ l , m i d ] [l, mid] [l,mid]之间
根据这个二段性,我们能二分出ans,使得边权之和/边权之和的最大值 = ans
现在的问题是check如何实现?
整理不等式,如下图:
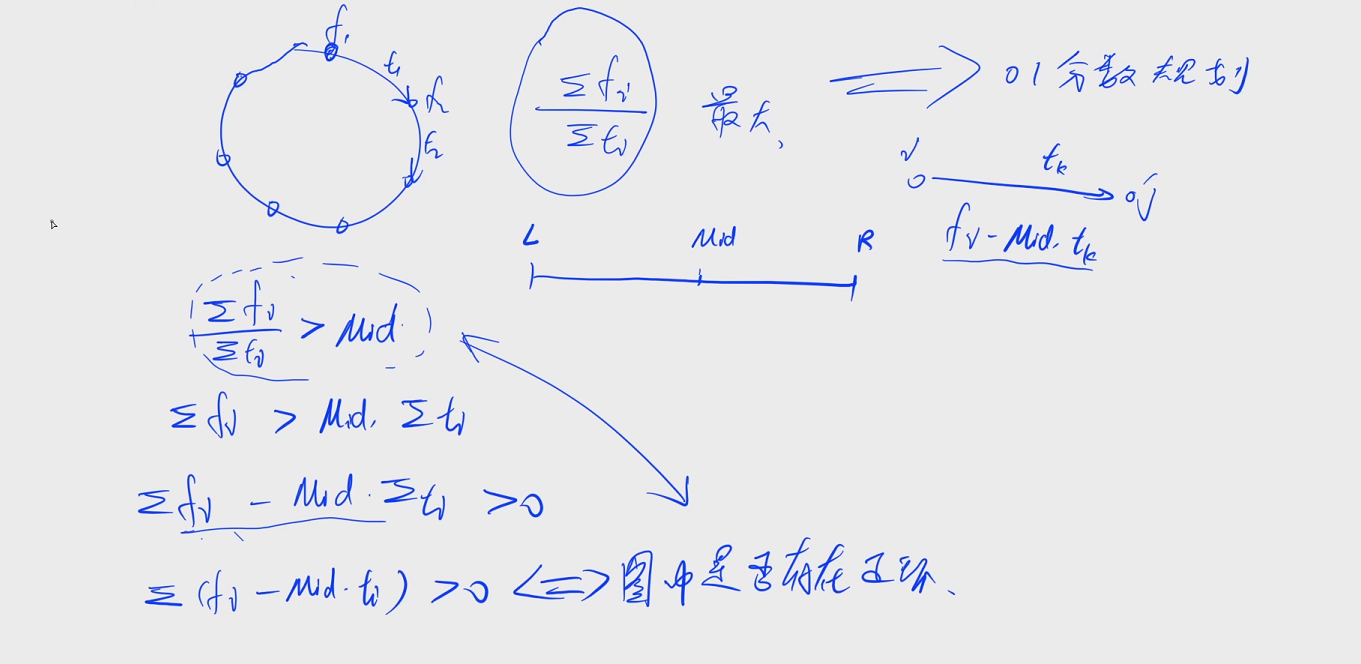
一个常用的技巧:若图中的环既有点权又有边权,那么可以将点权加到出边或者入边上
那么不等式的求和可以提到外面,结合这个技巧,将点权和边权结合
若一条边由x->y,权值为w,那么将其权值设置为 f x − m i d ∗ w f_x-mid*w fx−mid∗w, f x f_x fx为x的点权
问题就转换成了图中是否存在一个正环?
求正环只要修改三角不等式即可:dis[y] < dis[x] + w[i]
总结下:check判断图中是否存在一个环,其点权之和/边权之和大于等于mid,转换成图中是否存在一个正环(或权值和为0的环),若存在,则l = mid,否则r = mid,
- 思考题目的二段性
- 根据不等式重置边/点权
- 根据不等式判断题目的具体问题:负环/最小生成树/最短路
#include <iostream>
#include <cstring>
using namespace std;const int N = 1010, M = 5010;
int h[N], e[M], ne[M], w[M], idx;
int f[N];
double dis[N];
int cnt[N]; bool st[N];
int q[N];int n, m;void add(int x, int y, int d)
{e[idx] = y, ne[idx] = h[x], w[idx] = d, h[x] = idx ++ ;
}bool check(double mid)
{memset(dis, 0, sizeof(dis));memset(cnt, 0, sizeof(cnt));int tt = 0, hh = 0;for (int i = 1; i <= n; ++ i ) st[i] = true, q[tt ++ ] = i;while (hh != tt){int x = q[hh ++ ];if (hh == N) hh = 0;st[x] = false;for (int i = h[x]; i != -1; i = ne[i]){int y = e[i];if (dis[y] <= dis[x] + f[x] - mid * w[i]){dis[y] = dis[x] + f[x] - mid * w[i];cnt[y] = cnt[x] + 1;if (cnt[y] >= n) return true;if(!st[y]){st[y] = true;q[tt ++ ] = y;if (tt == N) tt = 0;}}}}return false;
}int main()
{memset(h, -1, sizeof(h));scanf("%d%d", &n, &m);for (int i = 1; i <= n; ++ i ) scanf("%d", &f[i]);int x, y, d;for (int i = 0; i < m; ++ i ){scanf("%d%d%d", &x, &y, &d);add(x, y, d);}double l = 0, r = 1000;while (r - l > 1e-4){double mid = (l + r) / 2;if (check(mid)) l = mid;else r = mid;}printf("%.2lf\n", r);return 0;
}
debug:点权需要从数组1号下标开始读取
特殊建图与01分数规划+trick:1165. 单词环
1165. 单词环 - AcWing题库
估算一下这题的数据量,如果按照题意建图,不仅爆空间还会爆时间,所以这题需要考虑其他建图方式
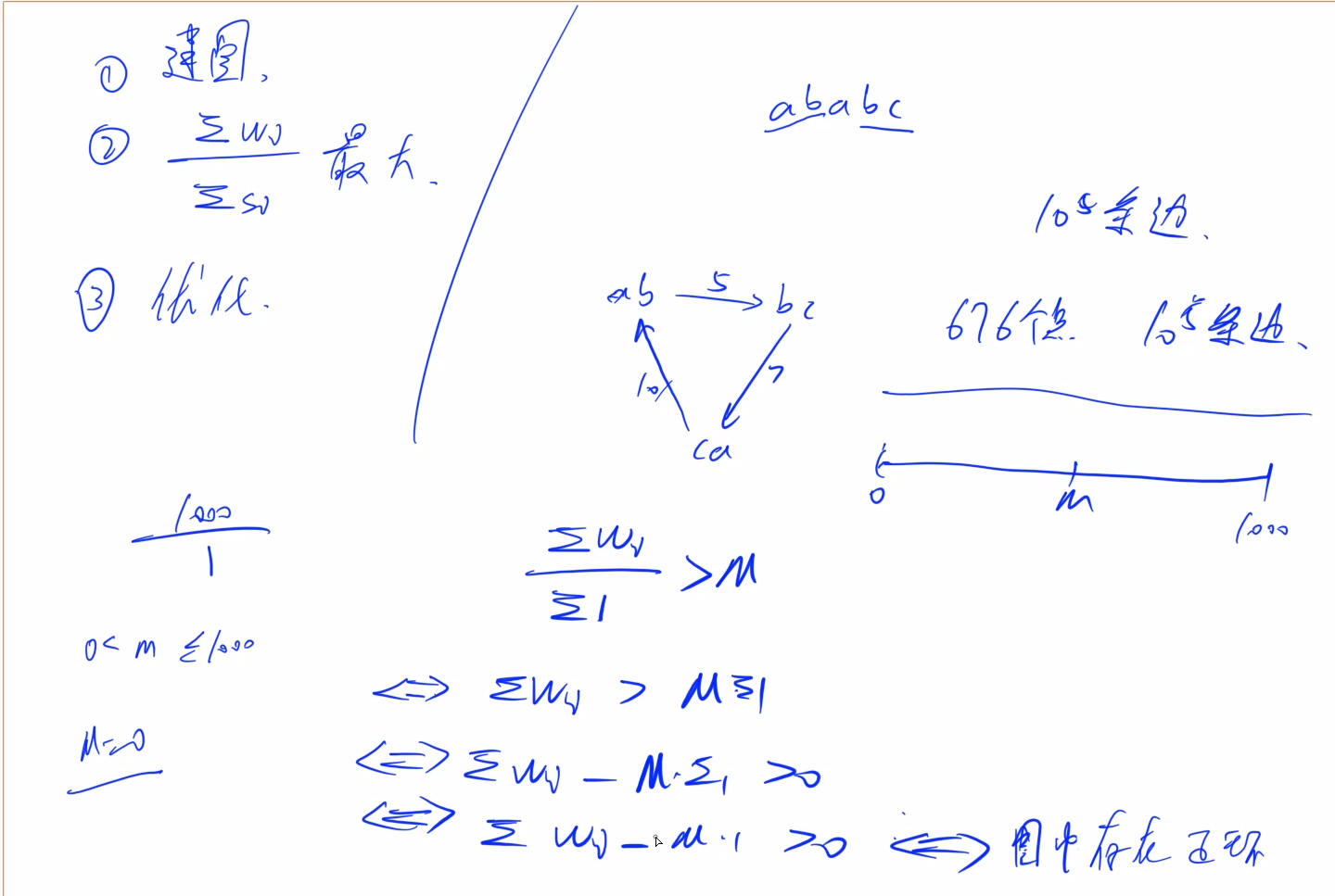
题目给定的建图方式是:单词为点,若两单词能相连,那么边的权值为1
考虑新的建图方式,以单词的前两个字符为起点,最后两个字符为终点,建立一条有向边,权值为单词的长度。这种建图方式中,点的数量最多为26 * 26,边的数量为 1 0 5 10^5 105
其次,题目要求环中所有单词的长度之和 / 环中的单词数量最大,显然是01分数规划
二分答案,答案的范围是 ( 0 , 1000 ] (0, 1000] (0,1000],最大的答案为每个单词长度都是1000,而最小的答案0是取不到的,最小的情况应该是1,0用来表示无解
整理不等式,重新设置边权为 w i − 1 ∗ m i d w_i - 1 * mid wi−1∗mid,1是由环中点的数量累加后(第二个式子)再把累加提到外面(第三个等式)得到的
check:每次根据mid判断图中是否存在正环或零环,若存在返回true,反之返回false
trick:如果spfa更新了很多次还没有结束循环,那么有极大概率可以认为图中存在环,这里设置阈值为10000(点数的十几倍),当循环次数超过该值时,直接认为图中存在环、
不过这样的trick在正规比赛中不会出现
#include <iostream>
#include <cstring>
using namespace std;const int N = 27 * 27, M = 1e5 + 10;
int h[N], e[M], ne[M], w[M], idx;
double dis[N];
int cnt[N], q[N];
bool st[N];void add(int x, int y, int d)
{e[idx] = y, ne[idx] = h[x], w[idx] = d, h[x] = idx ++ ;
}bool check(double mid)
{memset(dis, 0, sizeof(dis));memset(cnt, 0, sizeof(cnt));int tt = 0, hh = 0, count = 0;for (int i = 0; i < N - 1; ++ i ) q[tt ++ ] = i, st[i] = true;while (hh != tt ){int x = q[hh ++ ];if (hh == N) hh = 0;st[x] = false;for (int i = h[x]; i != -1; i = ne[i]){int y = e[i];if (dis[y] <= dis[x] + w[i] - mid){cnt[y] = cnt[x] + 1;if (cnt[y] >= N) return true;if (++ count >= 10000) return true;dis[y] = dis[x] + w[i] - mid;if (!st[y]){st[y] = true;q[tt ++ ] = y;if (tt == N) tt = 0;}}}}return false;
}int main()
{int m;char str[1010];while (scanf("%d", &m), m){memset(h, -1, sizeof(h));idx = 0;for (int i = 0; i < m; ++ i ){scanf("%s", str);int len = strlen(str);if (len >= 2){int x = (str[0] - 'a') * 26 + str[1] - 'a';int y = (str[len - 2] - 'a') * 26 + str[len - 1] - 'a';add(x, y, len);}}double l = 0, r = 1000;while (r - l > 1e-4){double mid = (l + r) / 2;if (check(mid)) l = mid;else r = mid;}if (r < 1e-4) puts("No solution");else printf("%.2lf\n", r);}return 0;
}
debug:dis数组的类型开成int,想着边的权值为整数,int就行,然而边权被重置,类型是浮点数
相关文章:

第三章 图论 No.6负环之01分数规划与特殊建图方式
文章目录 裸题:904. 虫洞01分数规划:361. 观光奶牛特殊建图与01分数规划trick:1165. 单词环 裸题:904. 虫洞 904. 虫洞 - AcWing题库 // 虫洞是负权且单向边,道路是正权且双向边,题目较裸,判…...

九、Spring 声明式事务学习总结
文章目录 一、声明式事务1.1 什么是事务1.2 事务的应用场景1.3 事务的特性(ACID)1.4 未使用事务的代码示例1.5 配置 Spring 声明式事务学习总结 一、声明式事务 1.1 什么是事务 把一组业务当成一个业务来做;要么都成功,要么都失败…...
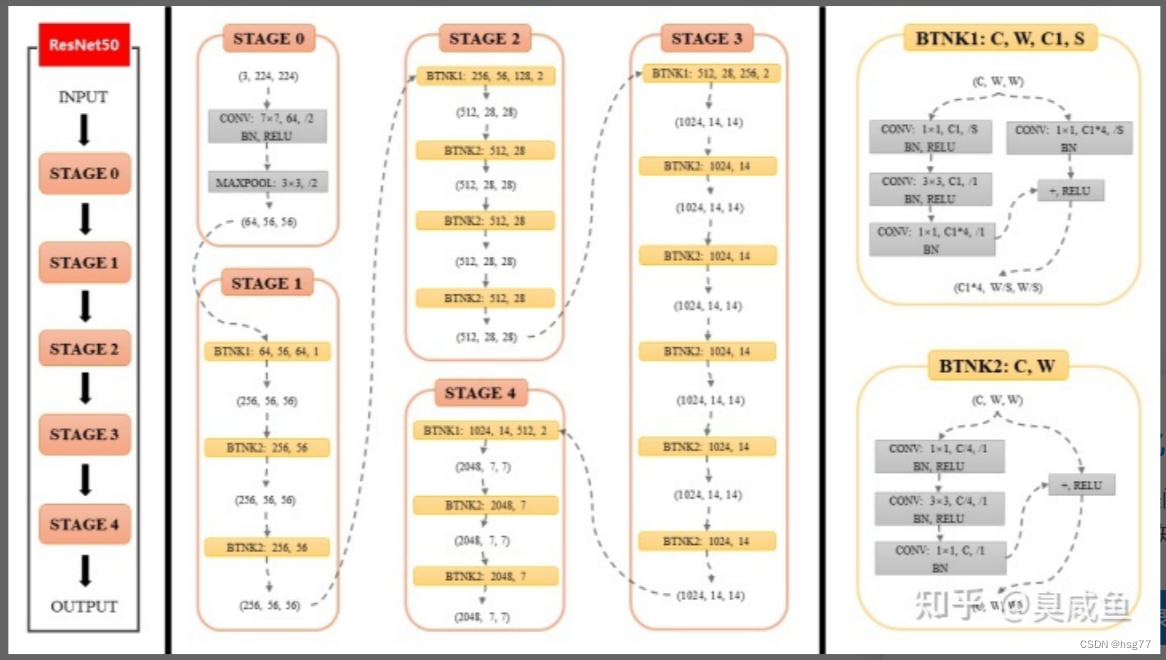
ResNet50卷积神经网络输出数据形参分析-笔记
ResNet50卷积神经网络输出数据形参分析-笔记 ResNet50包含多个模块,其中第2到第5个模块分别包含3、4、6、3个残差块 5049个卷积(3463)*31和一个全连接层 分析结果为: 输入数据形状:[10, 3, 224, 224] 最后输出结果:linear_0 [10,…...
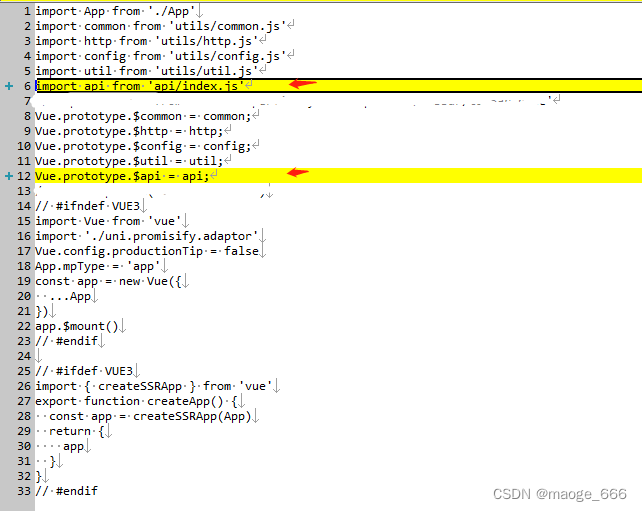
uniapp 微信小程序 封装公共的请求js(api版本)
一、新建api文件夹 在项目目录下创建api文件夹,内放files跟index.js文件夹,files文件夹内放每个页面对应的js请求接口 1、index.js /*** api接口的统一出口*/ const api {}; const requireComponent require.context(./files, false, /\.js$/) requi…...
格式化后数据恢复,教你3个实用方法!
“格式化后数据还能恢复吗?前几天因为我的电脑中了病毒,我不得不将它进行格式化操作。但是我电脑里有很多比较重要的文件,有什么方法可以帮我恢复电脑中的文件吗?求解答!” 格式化是一种比较常见的数据清除方法&#x…...
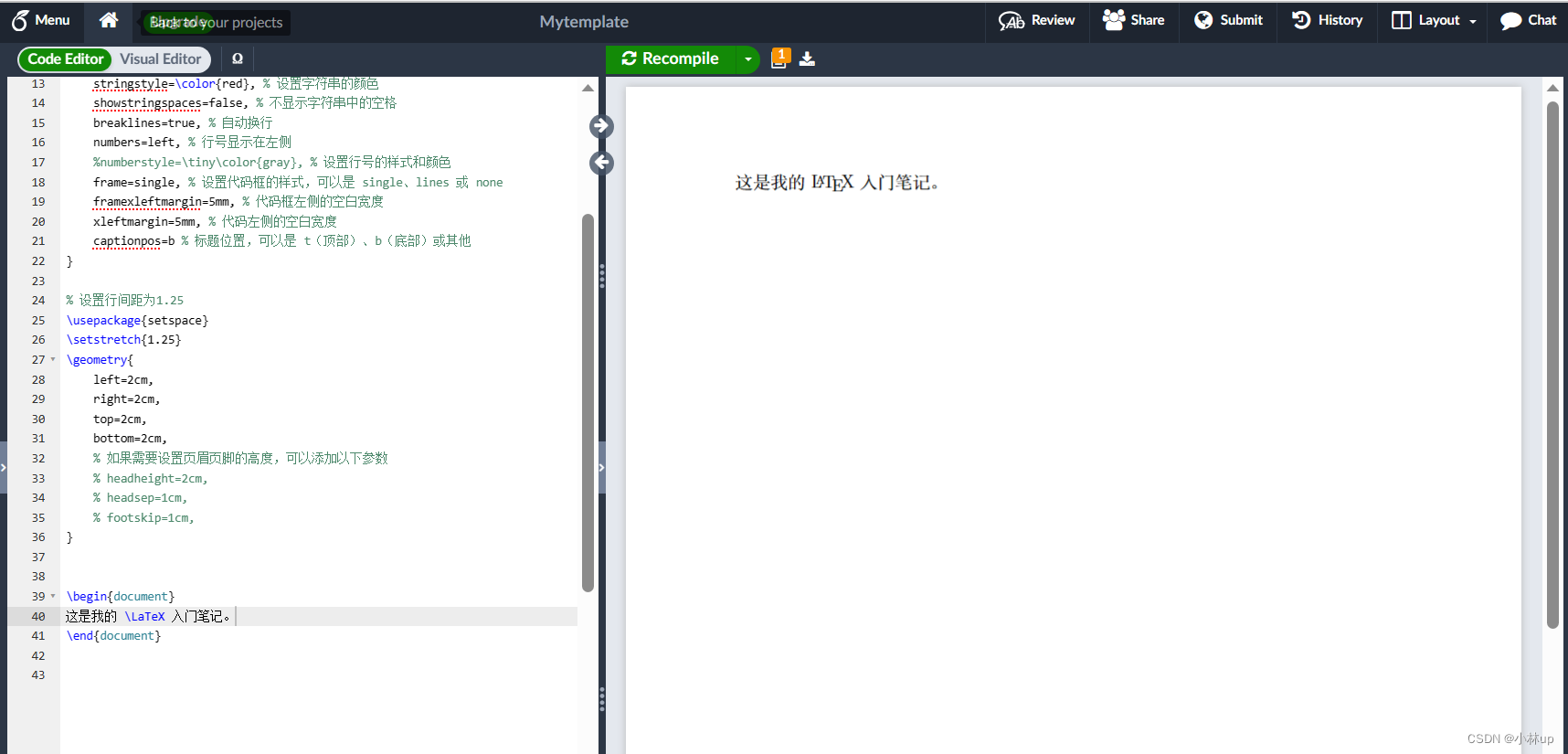
LaTex使用技巧21:设置中文环境、字体、行间距和页边距
我在Overleaf上编写我的中文LaTex,设置了中文环境,字体、行间距以及页间距,记录一下方便以后查询。 使用中文环境命令为: \usepackage{xeCJK}可以使用Overleaf上支持的中文字体Fonts for CJK Chinese,设置字体的命令…...

【RabbitMQ】golang客户端教程3——发布订阅(使用fanout交换器)
发布订阅 在上一个教程中,我们创建了一个工作队列。工作队列背后的假设是每个任务只传递给一个工人。在这一部分中,我们将做一些完全不同的事情——我们将向多个消费者传递一个消息。这就是所谓的“订阅/发布模式”。 为了说明这种模式,我们…...

图像处理学习笔记
图像处理的流程:获取图像-分割区域-特征提取。 嵌入式工业读码器 :包括DM码、QR码、vericode码 Blob分析与形态学 1.Blob区域是Blobs这一数据类型在halcon中的一种贴切的表达形式。 采集图像-区域分割,最后通过特征(如圆度、面积、…...

87端口无法访问-GoogleChrome非安全端口列表
以下为Google Chrome 默认非安全端口列表 平时我们服务器尽量不要开启这些端口,会产生访问不了的错误! 1, // tcpmux7, // echo9, // discard11, // systat13, // daytime15, // netstat17, // qotd19, // chargen20, // ftp data…...

pyautogui 配合 selenium 实现桌面坐标系定位元素坐标,模拟真实鼠标行为
pyautogui 配合 selenium 实现桌面坐标系定位元素坐标,模拟真实鼠标行为。 场景:当我需要点击某个元素,或者触发浏览器的自动填充账号密码时,自动化点击无效。但是想要模拟真实鼠标点击又需要元素的坐标通过pyautogui来实现。通过…...
c#设计模式-创建型模式 之 工厂模式
前言: 工厂模式(Factory Pattern)是一种常用的对象创建型设计模式。该模式的主要思想是提供一个创建对象的接口(也可以是抽象类、静态方法等),将实际创建对象的工作推迟到子类中进行。这样一来,…...
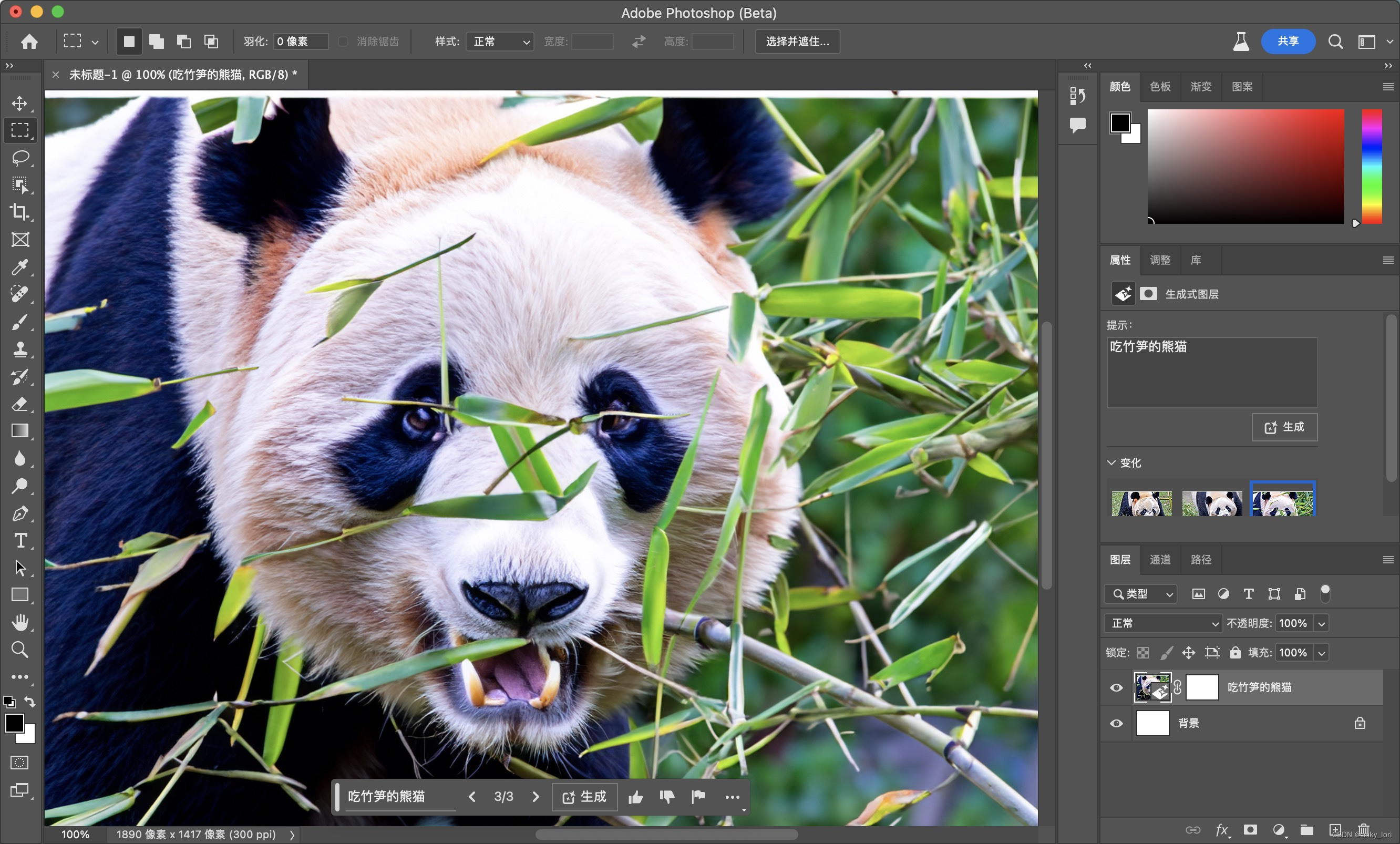
Photoshop 2023 25.0beta「Mac」
Photoshop 2023是一款专业图像处理软件,它主要用于图像编辑、合成和设计等方面。 Photoshop beta创新式填充的功能特色包括: 自动识别和删除对象:该功能可以自动识别图像中的对象,并用周围的图像填充空白部分,使图像看…...

机器学习基础07-模型选择01-利用scikit-learn 基于Pima 数据集对LogisticRegression算法进行评估
选择合适的模型是机器学习和深度学习中非常重要的一步,它直接影响到模型的性能和泛化能力。 “所有模型都是坏的,但有些模型是有用的”。建立模型之后就要去评 估模型,确定模型是否有用。模型评估是模型开发过程中不可或缺的一部 分ÿ…...

单片机实现动态内存管理
1.简介 多数传统的单片机并没有动态内存管理功能。单片机通常具有有限的存储资源,包括固定大小的静态RAM(SRAM)用于数据存储和寄存器用于特定功能。这些资源在编译时被分配并且在程序的整个生命周期中保持不变。 2.动态内存管理好处 灵活性和…...

(JS逆向专栏十一)某融平台网站登入RSA
声明: 本文章中所有内容仅供学习交流,严禁用于商业用途和非法用途,否则由此产生的一切后果均与作者无关,若有侵权,请联系我立即删除! 名称:点融 目标:登入参数 加密类型:RSA 目标网址:https://www.dianrong.com/accoun…...
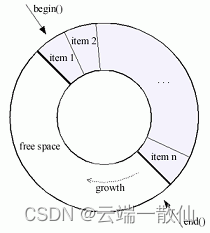
c++ boost circular_buffer
boost库中的 circular_buffer顾名思义是一个循环缓冲器,其 capcity是固定的当容量满了以后,插入一个元素时,会在容器的开头或结尾处删除一个元素。 circular_buffer为了效率考虑,使用了连续内存块保存元素 使用固定内存&#x…...

网络编程——端口
端口 一、端口概述 TCP/IP 协议采用端口标识通信的进程 用于区分一个系统里的多个进程 二、端口特点 1、对于同一个端口,在本同系统中对应着不同的进程 2、对于同一个系统,一个端口只能被一个进程拥有 3、一个进程拥有一个端口后,传输层送…...
【网络】自定义协议 | 序列化和反序列化 | Jsoncpp
本文首发于 慕雪的寒舍 以tcpServer的计算器服务为例,实现用jsoncpp来进行序列化和反序列化 阅读本文之前,请先阅读 自定义协议 | 序列化和反序列化 | 以tcpServer为例 1.安装jsoncpp 我所用的系统是centos7.6,先用下面的命令查找相关的包 …...

PHP实践:用openssl打造安全可靠的API签名验证系统
🏆作者简介,黑夜开发者,全栈领域新星创作者✌,阿里云社区专家博主,2023年6月csdn上海赛道top4。 🏆数年电商行业从业经验,历任核心研发工程师,项目技术负责人。 🏆本文已…...
每天一道leetcode:剑指 Offer 50. 第一个只出现一次的字符(适合初学者)
今日份题目: 在字符串 s 中找出第一个只出现一次的字符。如果没有,返回一个单空格。 s 只包含小写字母。 示例1 输入:s "abaccdeff" 输出:b 示例2 输入:s "" 输出: 提示 0 …...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

LabVIEW双光子成像系统技术
双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制,展现出显著的技术优势: 深层组织穿透能力:适用于活体组织深度成像 高分辨率观测性能:满足微观结构的精细研究需求 低光毒性特点:减少对样本的损伤…...

android RelativeLayout布局
<?xml version"1.0" encoding"utf-8"?> <RelativeLayout xmlns:android"http://schemas.android.com/apk/res/android"android:layout_width"match_parent"android:layout_height"match_parent"android:gravity&…...

通过 Ansible 在 Windows 2022 上安装 IIS Web 服务器
拓扑结构 这是一个用于通过 Ansible 部署 IIS Web 服务器的实验室拓扑。 前提条件: 在被管理的节点上安装WinRm 准备一张自签名的证书 开放防火墙入站tcp 5985 5986端口 准备自签名证书 PS C:\Users\azureuser> $cert New-SelfSignedCertificate -DnsName &…...

nnUNet V2修改网络——暴力替换网络为UNet++
更换前,要用nnUNet V2跑通所用数据集,证明nnUNet V2、数据集、运行环境等没有问题 阅读nnU-Net V2 的 U-Net结构,初步了解要修改的网络,知己知彼,修改起来才能游刃有余。 U-Net存在两个局限,一是网络的最佳深度因应用场景而异,这取决于任务的难度和可用于训练的标注数…...
