创意编程py模拟题
前言:好久没写博客了,来水好好写一篇
注:本篇文章为py,不是c++
1、敲七 版本1
题目:
题目描述
输出7和7的倍数,还有包含7的数字例如(17,27,37…70,71,72,73…)。当然,这些数是无限的,所以我们加上一个上限N。即输出不大于N的敲七数。
输入格式
第1行:1个整数N。(N不大于30000)
输出格式
若干行,每行一个敲七数。按从小到大的顺序排列。
样例
样例输入
20
样例输出
7
14
17
分析
一个数一个数的排查
AC代码
n=int(input())
for i in range(7,n+1):if i % 7 == 0 :print(i)else:j = iwhile j <= n:if j % 10 == 7:print(i)breakj = j // 10;if j == 0:break
2、韩信点兵
题目
题目描述
相传韩信才智过人,从不直接清点自己军队的人数,只要让士兵先后以三个人一排,五人一排,七人一排地变换队形,而他每次只掠一眼队伍的队尾就知道总人数了。输入3个非负整数a,b,c,表示每种队尾的人数(a<3,b<5,c<7),输出总人数的最小值(或报告无解)。已知总人数不小于10,不超过100。
//请有基础的同学写中国剩余定理
输入格式
2 1 6
输出格式
41
样例
样例输入
2 1 3
样例输出
no answer
分析
因为人数再100以内,所以工程量很小,从1枚举到100便可
a,b,c=map(int,input().split())
for i in range(1,101):if(i%3==a and i%5==b and i%7==c):print(i)sys.exit()
print("no answer")
3、完全数
题目
题目描述
若某个自然数的所有小于自身的因数之和恰好等于其自身,则该自然数称为一个完全数。试编程找出m~n间的完全数。
输入格式
二个整数m、n。(1≤m,n≤20000)
输出格式
每行一个完全数,最后一个数为完全数的个数
样例
样例输入
1 10
样例输出
6
1
分析
这道题要注意一点,因为工程量很大,所以暴力有可能超时,所以要找到完全数末尾为6/8的特点(性质)
AC代码
n,m=map(int,input().split())
w=0
for i in range(n,m+1):s=0for j in range(1,i//2+1):#print(j)if i%10==8 or i%10==6 :#判断末尾为6/8if i%j==0 :s+=jif s>i:breakif s==i:print(i)w+=1
print(w)
4、鸡兔问题
题目
题目描述
鸡兔关在同一笼中,读入总脚数及头数,编程输出鸡兔各有多少只。
输入格式
共一行,二个数N和M,分别表示脚数及头数
输出格式
共一行,两个整数,鸡兔各多少只,两数之间用一空格分开
样例
样例输入
40 16
样例输出
12 4
AC代码
b, a = map(int, input().split(' '))
for i in range(1, a):x = iy = a - xif 2 * x + 4 * y == b:print("{} {}".format(x, y))break相关文章:

创意编程py模拟题
前言:好久没写博客了,来水好好写一篇 注:本篇文章为py,不是c 1、敲七 版本1 题目: 题目描述 输出7和7的倍数,还有包含7的数字例如(17,27,37…70,71&#…...
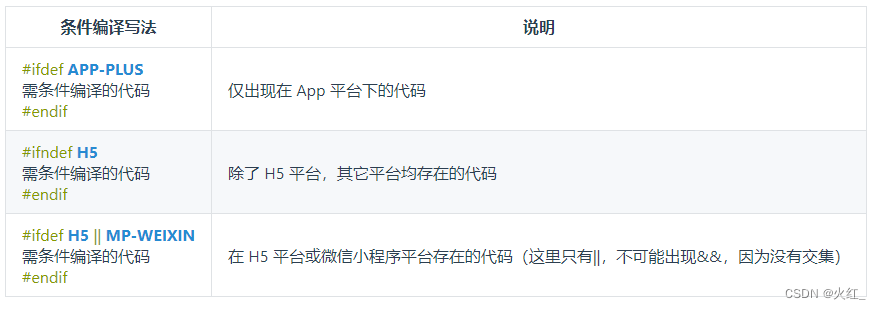
uniapp中条件编译
官方:https://uniapp.dcloud.net.cn/tutorial/platform.html#%E8%B7%A8%E7%AB%AF%E5%85%BC%E5%AE%B9 #ifndef H5 代码段… #endif 表示除了H5其他都可以编译 #ifdef H5 代码段… #endef 表示只能编译H5,其他的都不能编译 其他编译平台请查看官方文档。 …...

封装 YoloV5 detect.py 成 Python 库以供 python 程序使用
本项目地址 Github 本项目地址 Github Introduction YoloV5 作为 YoloV4 之后的改进型,在算法上做出了优化,检测的性能得到了一定的提升。其特点之一就是权重文件非常的小,可以在一些配置更低的移动设备上运行,且提高速度的同时…...

PostgreSQL , PostGIS , 球坐标 , 平面坐标 , 球面距离 , 平面距离
标签 PostgreSQL , PostGIS , 球坐标 , 平面坐标 , 球面距离 , 平面距离 背景 PostGIS中有两种常用的空间类型geometry和geography,这两种数据类型有什么差异,应该如何选择? 对于GIS来说,首先是坐标系,有两种&#…...

K3S 系列文章-5G IoT 网关设备 POD 访问报错 DNS ‘i/o timeout‘分析与解决
开篇 《K3s 系列文章》《Rancher 系列文章》 问题概述 20220606 5G IoT 网关设备同时安装 K3S Server, 但是 POD 却无法访问互联网地址,查看 CoreDNS 日志提示如下: ... [ERROR] plugin/errors: 2 update.traefik.io. A: read udp 10.42.0.3:38545-&…...

社会工程学介绍
目录前言手段和术语假托在线聊天/电话钓鱼下饵(Baiting)等价交换同情心尾随(Tailgating or Piggybacking)社交工程学的演进钓鱼式攻击电脑蠕虫垃圾邮件特别人物总结前言 在信息安全方面,社会工程学是指对人进行心理操…...

干货 | 有哪些安慰剂按钮的设计?
仔细观察我们的生活,你会发现处处都是安慰剂按钮,ATM的点钞声、开启空调的呼呼声,这些都对用户心里产生了有意的引导作用,当你打开了空调按钮,先播放声音会让你感觉你按下的按钮起到了作用。 我们的大脑不喜欢杂乱无章…...

LeetCode 每日一题 2023/2/13-2023/2/19
记录了初步解题思路 以及本地实现代码;并不一定为最优 也希望大家能一起探讨 一起进步 目录2/13 1234. 替换子串得到平衡字符串2/14 1124. 表现良好的最长时间段2/15 1250. 检查「好数组」2/16 2341. 数组能形成多少数对2/17 1139. 最大的以 1 为边界的正方形2/18 1…...

SAP 关于多种语言配置
怎样才能在登录时选择自己需要的语言登录呢?虽然这个问题对很多人来说可能根本就算不上问题,但对很多新手来说可能却是很想尽快解决的问题。 曾经有位Puber说有个很简单的办法,但可惜的是在我一直没找到这个办法。今天看到一份资料ÿ…...
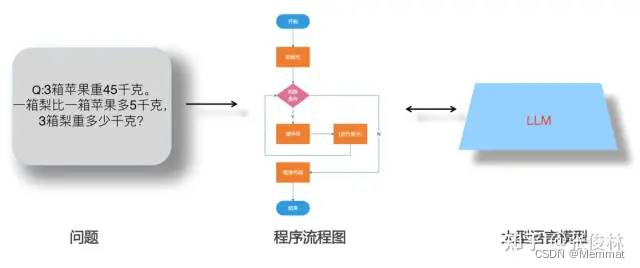
万字长文讲述由ChatGPT反思大语言模型的技术精要
文|张俊林 源|知乎张俊林 导读:ChatGPT出现后惊喜或惊醒了很多人。惊喜是因为没想到大型语言模型(LLM,Large Language Model)效果能好成这样;惊醒是顿悟到我们对LLM的认知及发展理念,…...

SpringBoot静态资源访问
静态资源路径 类路径下:/resources/static/、/resources/public/、/resources/resources/、/resources/META-INF/resources 这些路径下的资源均可直接访问;通过 http://ip:port/资源名称 访问即可 可在配置文件中对访问路径和访问拦截规则进行设置&…...
【物联网】智慧农业病虫害精准辨识竞赛思路及代码分享
来源:投稿 作者:LSC 编辑:学姐 比赛官网: https://www.dataglobal.cn/cmpt/signUpInfo200.html 任务描述 请参赛者设计智慧农业病虫害检测系统,给出一体化问题解决方案,鼓励参赛选手结合某一果园/农作物实际情况建立…...

Properties类读取配置文件
文章目录前言一、Properties类的使用 :1、创建sk.properties文件2、编写读取 properties 属性文件,并输出属性值。3、运行结果总结前言 Properties类的介绍 : 在Java中提供了 java.util.Properties 类,来读取 .properties 属性文件。在程序调用 Propert…...

知其然更要知其所以然,聊聊SQLite软件架构
SQLite是一个非常受欢迎的数据库,在数据库排行榜中已经进入前十的行列。这主要是因为该数据库非常小巧,而且可以支持Linux、Windows、iOS和Andriod的主流的操作系统。 SQLite非常简单,是一个进程内的动态库数据库。其最大的特点是可以支持不同…...
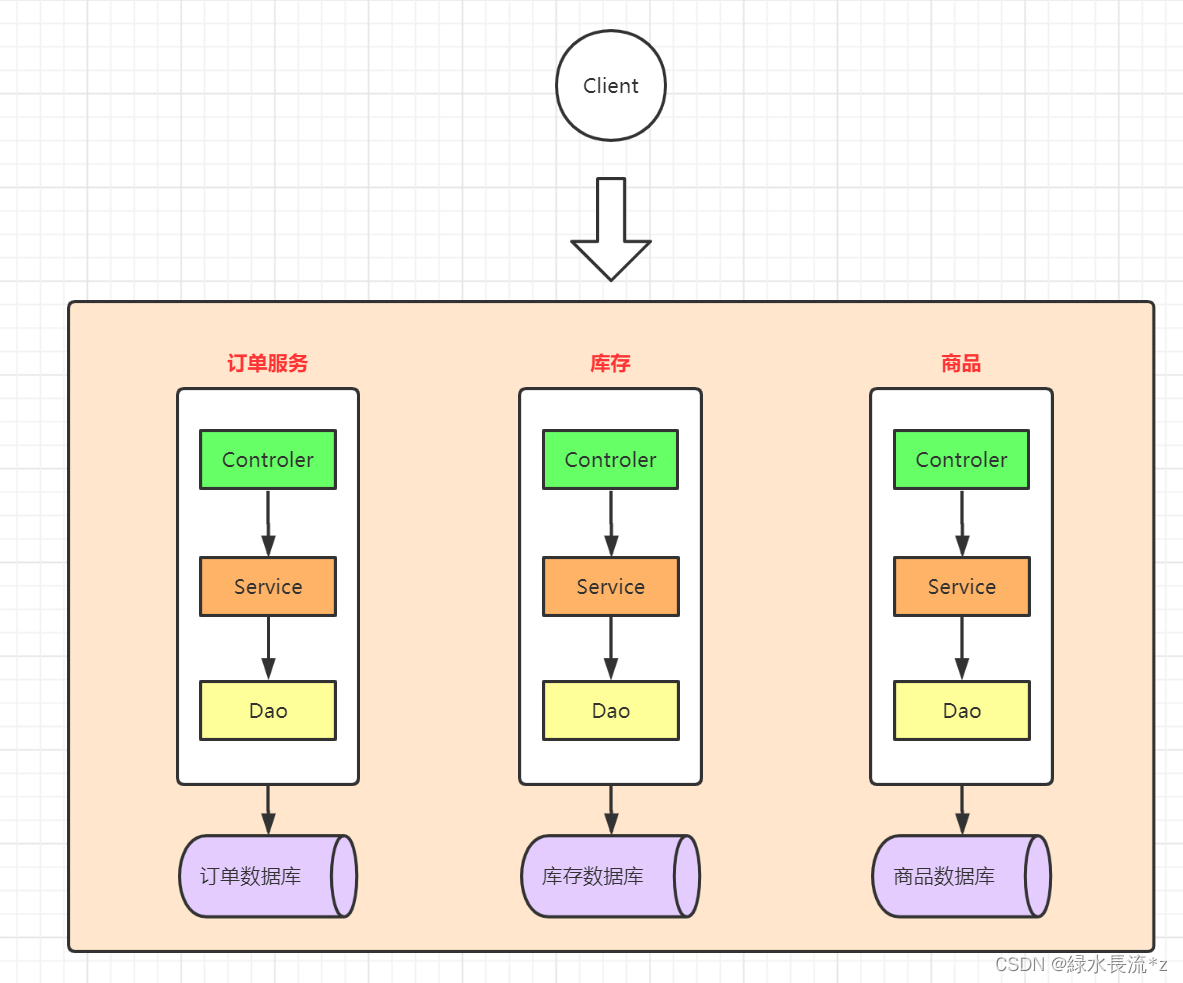
微服务架构的演变
文章目录1.1 系统架构的演变过程1.1.1 单体应用架构1.1.2 垂直应用架构1.1.3 分布式架构1.1.4 SOA架构1.1.5 微服务架构1.2 微服务架构设计原则1.2.1 AKF拆分原则1.2.1.1 X轴扩展(水平复制)1.2.1.2 Y轴扩展(模块拆分)1.2.1.3 Z轴扩…...
使用html-to-image代替html2canvas,结合jspdf实现下载pdf(下载截图下载前端dom元素)
一、问题 一开始的时候,准备使用html2canvasjspdf来实现的,但是遇到了一个麻烦的问题,在其他项目中使用html2canvas没有任何问题,但是在要开发的项目中使用,就给我报错,是真滴烦。 html2canvas报错 Uncau…...

云环境渗透测试的重要性
🌕写在前面 🎉欢迎关注🔎点赞👍收藏⭐️留言📝 ✉️今日分享: “在这个世上,除了极稀少的例外,我们其实只有两种选择:要么是孤独,要么就是庸俗。” 随着云计…...
)
ROS2 入门应用 请求和应答(Python)
ROS2 入门应用 请求和应答(Python)1. 创建功能包1. 创建功能包2. 创建源文件2.1. 服务端2.2. 客户端3. 添加依赖关系4. 添加入口点5. 编译和运行1. 创建功能包 1. 创建功能包 在《ROS2 入门应用 工作空间》中已创建和加载了ros2_ws工作空间 在《ROS2 入…...

是德Keysight E4991A/e4991B射频阻抗/材料分析仪
Keysight E4991A 射频阻抗/材料分析仪提供终极阻抗测量性能和强大的内置分析功能。它将为评估 3 GHz 范围内组件的组件和电路设计人员的研发提供创新。E4991A 使用 RF-IV 技术,而不是反射测量技术,可在宽阻抗范围内进行更精确的阻抗测量。基本阻抗精度为…...
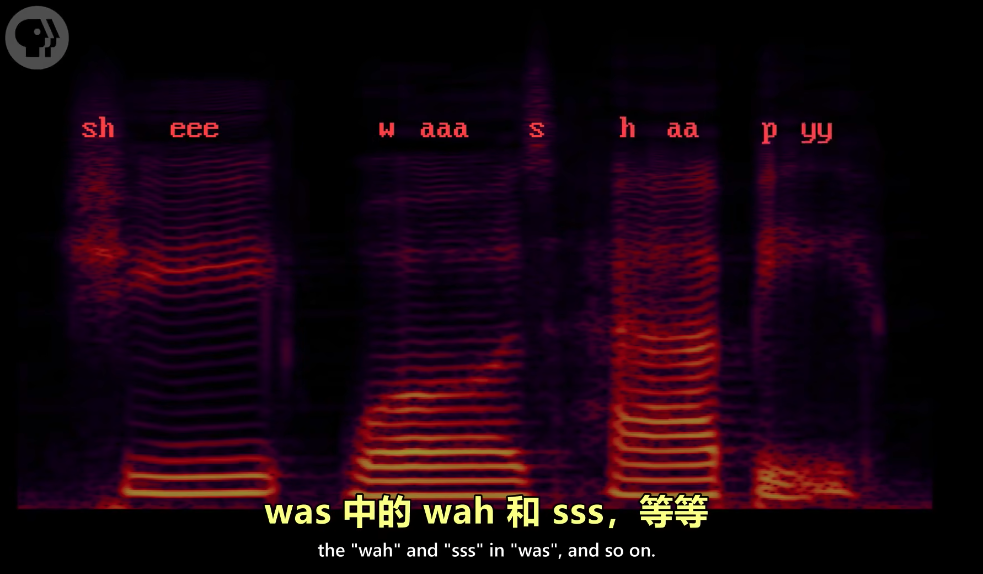
这才是计算机科学_人工智能
人工智能一、前言二、ML2.1 分类2.1.1 决策树2.2.2 支持向量机2.2.3 人工神经网络三、计算机视觉3.1 Prewitt算子3.2 Viola-Jones 人脸检测算法3.3 卷积神经网络四、自然语言处理4.1 知识图谱4.2 语音识别一、前言 之前讲了计算机从发展到现在的过程,计算机很适合做…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

【从零开始学习JVM | 第四篇】类加载器和双亲委派机制(高频面试题)
前言: 双亲委派机制对于面试这块来说非常重要,在实际开发中也是经常遇见需要打破双亲委派的需求,今天我们一起来探索一下什么是双亲委派机制,在此之前我们先介绍一下类的加载器。 目录 编辑 前言: 类加载器 1. …...

日常一水C
多态 言简意赅:就是一个对象面对同一事件时做出的不同反应 而之前的继承中说过,当子类和父类的函数名相同时,会隐藏父类的同名函数转而调用子类的同名函数,如果要调用父类的同名函数,那么就需要对父类进行引用&#…...

ZYNQ学习记录FPGA(一)ZYNQ简介
一、知识准备 1.一些术语,缩写和概念: 1)ZYNQ全称:ZYNQ7000 All Pgrammable SoC 2)SoC:system on chips(片上系统),对比集成电路的SoB(system on board) 3)ARM:处理器…...
