数据结构 | 利用二叉堆实现优先级队列
目录
一、二叉堆的操作
二、二叉堆的实现
2.1 结构属性
2.2 堆的有序性
2.3 堆操作
队列有一个重要的变体,叫作优先级队列。和队列一样,优先级队列从头部移除元素,不过元素的逻辑顺序是由优先级决定的。优先级最高的元素在最前,优先级最低的元素在最后。因此,当一个元素入队时,它可能直接被移到优先级队列的头部。
实现优先级队列的经典方法是使用叫作二叉堆的数据结构。二叉堆的入队操作和出队操作均可达到。
二叉堆有两个常见的变体:最小堆(最小的元素一直在队首)与最大堆(最大的元素一直在队首)。
本篇文章实现的是最小堆。
一、二叉堆的操作
我们将实现以下基本的二叉堆方法。
- BinaryHeap()新建一个空的二叉堆。
- insert(k)往堆中加入一个新元素。
- findMin()返回最小的元素,元素留在堆中。
- delMin()返回最小的元素,并将该元素从堆中移除。
- isEmpty()在堆为空时返回True,否则返回False。
- size()返回堆中元素的个数。
- buildHeap(list)根据一个列表创建堆。
>>> from pythonds.trees import BinaryHeap
>>> bh=BinaryHeap()
>>> bh.insert(5)
>>> bh.insert(7)
>>> bh.insert(3)
>>> bh.insert(11)
>>> print(bh.delMin())
3
>>> print(bh.delMin())
5
>>> print(bh.delMin())
7
>>> print(bh.delMin())
11二、二叉堆的实现
2.1 结构属性
为了使二叉树能够高效地工作,我们利用树的对数性质来表示它。为了保证对数性能,必须维持树的平衡。平衡的二叉树是指,其根节点的左右子树含有数量大致相等的节点。在实现二叉堆时,我们通过创建一颗完全二叉树来维持树的平衡。在完全二叉树中,除了最底层,其他每一层的节点都是满的。在最底层,我们从左往右填充节点。
完全二叉树的另一个有趣之处在于,可以用一个列表来表示它,而不需要采用“列表之列表”或“节点与引用”表示法。由于树是完全的,因此,因此对于在列表中处于位置p的节点来说,它的左子节点正好处于位置2p;同理,右子节点处于位置2p+1。若要找到树中任意节点的父节点,只需使用python的整数除法即可。给定列表中位置n处的节点,其父节点的位置就是n/2。
2.2 堆的有序性
我们用来存储堆元素的方法依赖于堆的有序性。堆的有序性是指:对于堆中任意元素x及其父元素p,p都不大于x。
2.3 堆操作
新建二叉堆:
def __init__(self):self.heapList=[0]self.currentSize=0接下来实现insert方法。将元素加入列表的最简单、最高效的方法就是将元素追加到列表的末尾。追加操作的优点在于,它能保证完全数的性质,但缺点是很可能会破坏堆的结构性质。不过可以写一个方法,通过比较新元素与其父元素来重新获得堆的结构性质。如果新元素小于其父元素,就将二者交换。
perUp方法:
def perUp(self,i):while i//2>0:if self.heapList[i]<self.heapList[i//2]:tmp=self.heapList[i//2]self.heapList[i//2]=self.heapList[i]self.heapList[i]=tmpi=i//2向二叉堆中新加元素:
def insert(self,k):self.heapList.append(k)self.currentSize=self.currentSize+1self.perUp(self.currentSize)正确定义insert方法后,就可以编写delMin方法。既然堆的结构性质要求根节点是树的最小元素,那么查找最小值就很简单。delMin方法的难点在于,如果在移除根节点之后重获堆的结构性质和有序性。可以分两步重建堆。第一步,取出列表中的最后一个元素,将其移到根节点的位置。移动最后一个元素保证了堆的结构性质,但可能破坏二叉堆的有序性。第二步,将新的根节点沿着树推到正确的位置,以重获堆的有序性。
perDown方法和minChild方法:
def percDown(self,i):while (i*2)<=self.currentSize:mc=self.minChild(i)if self.heapList[i]>self.heapList[mc]:tmp=self.heapList[i]self.heapList[i]=self.heapList[mc]self.heapList[mc]=tmpi=mcdef minChild(self,i):if i*2+1>self.currentSize:return i*2else:if self.heapList[i*2]<self.heapList[i*2+1]:return i*2else:return i*2+1从二叉堆中删除最小的元素:
def delMin(self):retval=self.heapList[1]self.heapList[1]=self.heapList[self.currentSize]self.currentSize=self.currentSize-1self.heapList.pop()self.percDown(1)return retval根据元素列表构建堆:
def bulidHeap(self,alist):i=len(alist)//2self.currentSize=len(alist)self.heapList=[0]+alist[:]while (i>0):self.percDown(i)i=i-1相关文章:
数据结构 | 利用二叉堆实现优先级队列
目录 一、二叉堆的操作 二、二叉堆的实现 2.1 结构属性 2.2 堆的有序性 2.3 堆操作 队列有一个重要的变体,叫作优先级队列。和队列一样,优先级队列从头部移除元素,不过元素的逻辑顺序是由优先级决定的。优先级最高的元素在最前ÿ…...

Javascript怎样阻止事件传播?
在 JavaScript 中,可以使用事件对象的方法来阻止事件传播。事件传播指的是当一个元素上触发了一个事件,该事件会在事件流中传播到父元素或祖先元素,从而影响到它们。 事件传播有三个阶段:捕获阶段、目标阶段和冒泡阶段。阻止事件…...
web-csrf
目录 CSRF与XSS的区别: get请求 原理: pikachu为例 post请求 pikachu为例 CSRF与XSS的区别: CSRF是借用户的权限完成攻击,攻击者并没有拿到用户的权限,而XSS是直接盗取到了用户的权限 get请求 原理:…...
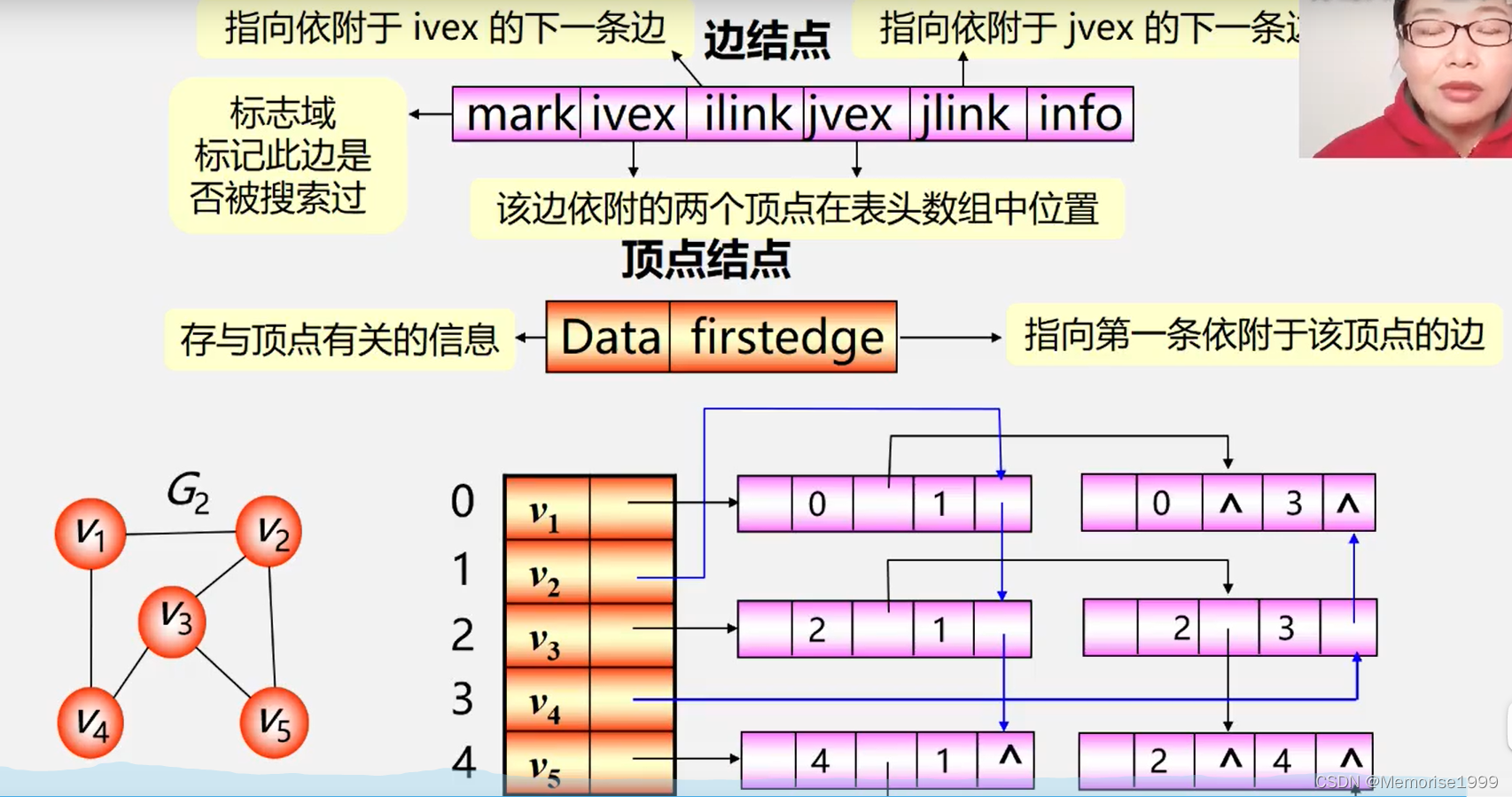
数据结构—图的存储结构
6.图 回顾:数据的逻辑结构 集合——数据元素间除 “同属于一个集合” 外,无其他关系。 线性结构——一个对一个,如线性表、栈、队列 树形结构——一个对多个,如树 图形结构——多个对多个,如图 6.1图的定义和术语 图:…...

Vue3 中 setup,ref 和 reactive 的理解
setup Vue3中使用了Composition API这种写法,使得所有的组合API函数都在此使用, 只在初始化时执行一次。 函数如果返回对象, 对象中的属性或方法, 模板中可以直接使用 ref 作用:定义一个数据的响应式 语法:const xxx ref(initValue) 一般用来…...

BL302嵌入式ARM控制器进行SQLite3数据库操作的实例演示
本文主要讲述了在钡铼技术BL302嵌入式arm控制器上运行 SQLite3 数据库的命令示例。SQLite3 是一个轻型的嵌入式数据库,不需要安装数据库服务器进程,占用资源低且处理速度快。 首先,需要将对应版本的 SQLite3 文件复制到设备的 /usr/ 目录下&…...
C++ 多线程:std::future
std::future std::future 简介示例1博客引用来源 std::future 简介 我们前面介绍的std::thread 是C11中提供异步创建多线程的工具,只能是异步运行任务,却无法获取任务执行的结果,一般都是依靠全局对象,全局对象在多线程下是及其不…...
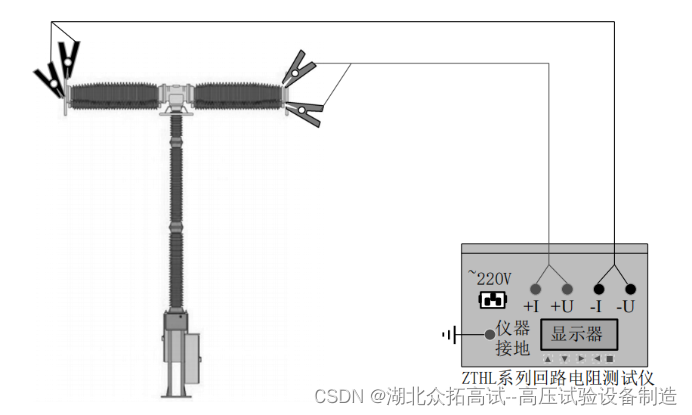
断路器回路电阻试验
试验目的 断路器回路电阻主要取决于断路器动、 静触头的接触电阻, 其大小直接影响正常 运行时的发热情况及切断短路电流的性能, 是反应安装检修质量的重要数据。 试验设备 回路电阻测试仪 厂家: 湖北众拓高试代销 试验接线 对于单断口的断路器, 通过断口两端的接线…...

Python中的CALL_FUNCTION指令
在Python字节码中,CALL_FUNCTION指令后跟的数字代表这次函数调用需要从栈上取出的参数的数量。具体来说,这个数字包括位置参数和关键字参数的数量。 这个数字的低两位表示位置参数的数量,然后每两位表示一个关键字参数的数量。因此ÿ…...
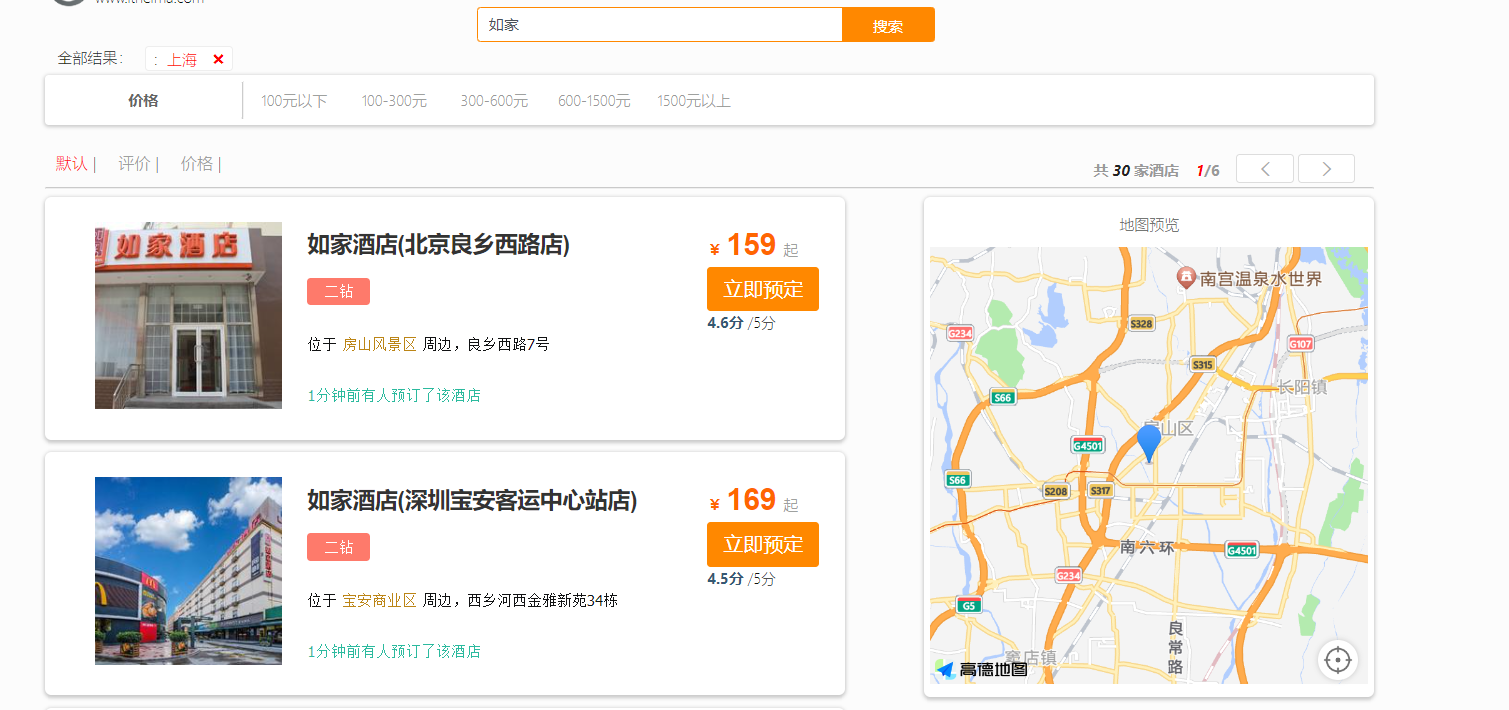
微服务——es数据聚合+RestClient实现聚合
数据聚合 聚合的种类 DSL实现Bucket聚合 如图所示,设置了10个桶,那么就显示了数量最多的前10个桶,品牌含有7天酒店的有30家, 品牌含有如家的也有30家。 修改排序规则 限定聚合范围 DSL实现Metrics聚合 如下案例要求对不同的品…...
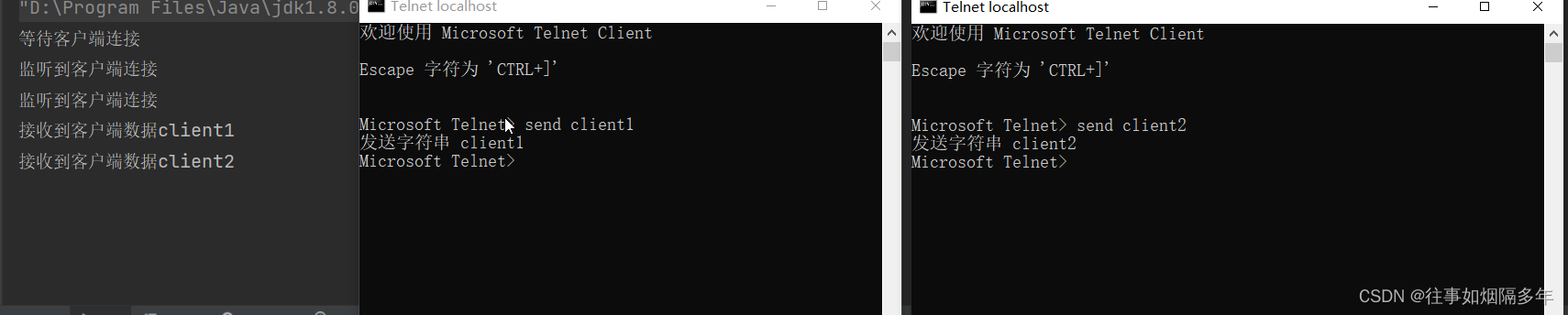
代码分析Java中的BIO与NIO
开发环境 OS:Win10(需要开启telnet服务,或使用第三方远程工具) Java版本:8 BIO 概念 BIO(Block IO),即同步阻塞IO,特点为当客户端发起请求后,在服务端未处理完该请求之前ÿ…...
网络安全(黑客)工作篇
一、网络安全行业的就业前景如何? 网络安全行业的就业前景非常广阔和有吸引力。随着数字化、云计算、物联网和人工智能等技术的迅速发展,网络安全的需求持续增长。以下是网络安全行业就业前景的一些关键因素: 高需求:随着互联网的…...
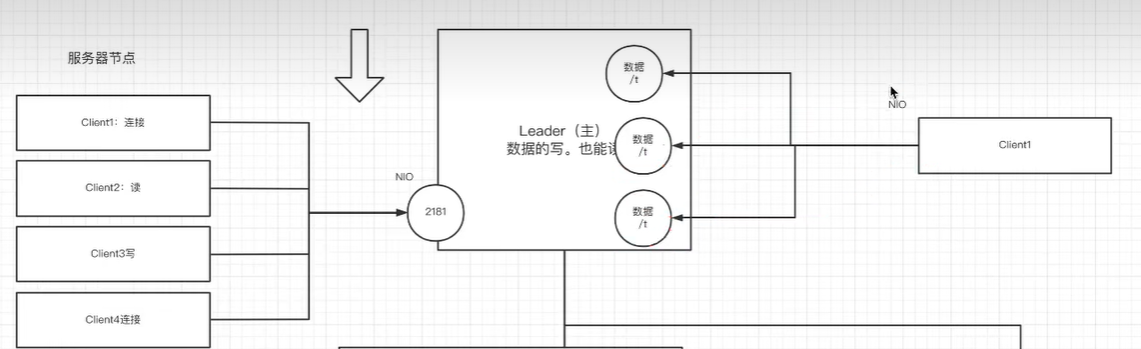
zookeeper入门学习
zookeeper入门学习 zookeeper应用场景 分布式协调组件 客户端第一次请求发给服务器2,将flag值修改为false,第二次请求被负载均衡到服务器1,访问到的flag也会是false 一旦有节点发生改变,就会通知所有监听方改变自己的值&#…...

VirtualEnv 20.24.0 发布
导读VirtualEnv 20.24.0 现已发布,VirtualEnv 用于在一台机器上创建多个独立的 Python 运行环境,可隔离项目之间的第三方包依赖,为部署应用提供方便,把开发环境的虚拟环境打包到生产环境即可,不需要在服务器上再折腾一…...
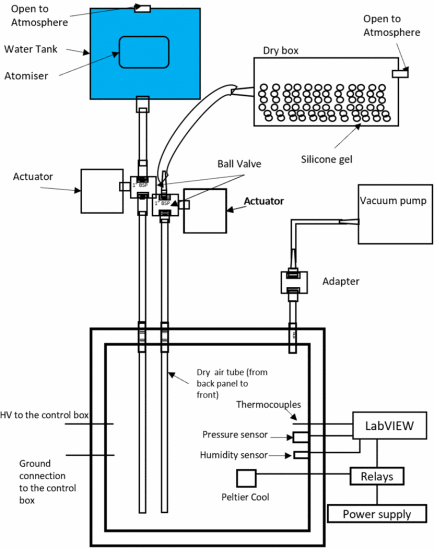
LabVIEW开发高压航空航天动力系统爬电距离的测试
LabVIEW开发高压航空航天动力系统爬电距离的测试 更多电动飞机MEA技术将发电,配电和用电集成到一个统一的系统中,提高了飞机的可靠性和可维护性。更多的电动飞机使用更多的电能来用电动替代品取代液压和气动系统。对车载电力的需求不断增加,…...
【论文阅读】基于深度学习的时序异常检测——Anomaly Transformer
系列文章链接 数据基础:多维时序数据集简介 论文一:2022 Anomaly Transformer:异常分数预测 论文二:2022 TransAD:异常分数预测 论文链接:Anomaly Transformer.pdf 代码链接:https://github.co…...

Java并发总结
1.创建线程三种方式 Runnable.Callable接口使用继承Thread类的方式创建多线程Runnable 和Callable区别 Callable规定(重写)的方法是call(),Runnable规定(重写)的方法是run()。Callable的任务执行后可返回值࿰…...
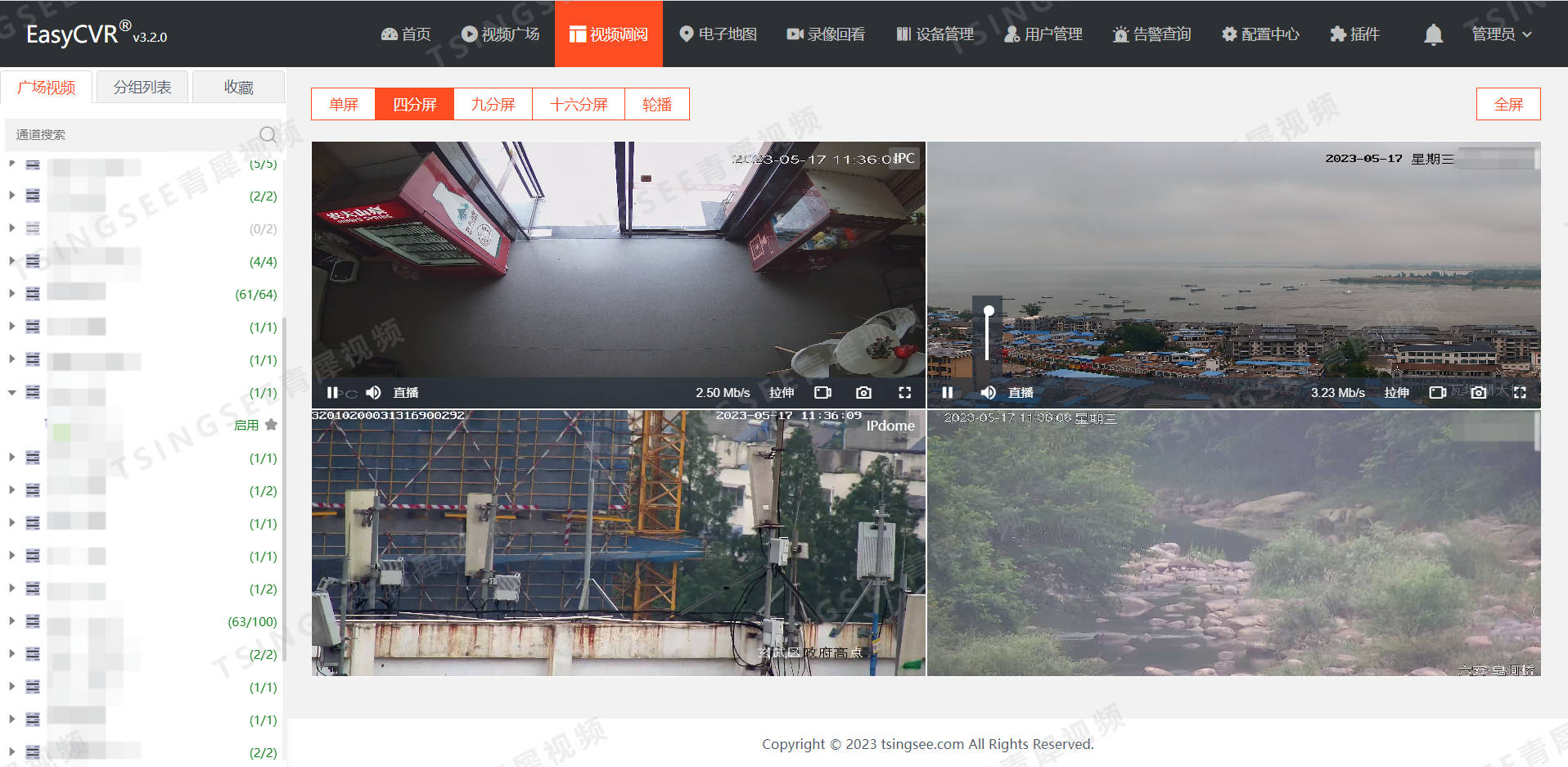
视频汇聚平台EasyCVR视频广场侧边栏支持拖拽
为了提升用户体验以及让平台的操作更加符合用户使用习惯,我们在EasyCVR v3.3版本中,支持面包屑侧边栏的广场视频、分组列表、收藏这三个模块拖拽排序,并且该操作在视频广场、视频调阅、电子地图、录像回放等页面均能支持。 TSINGSEE青犀视频…...

MyCat分片规则——范围分片、取模分片、一致性hash、枚举分片
1.范围分片 2.取模分片 范围分片和取模分片针对数字类型的字段可以,但是针对于字符串类型的字段时。这两种就不适用了。 3.一致性hash 4.枚举分片 默认节点指的是,如果我们向数据库表插入数据的时候,超出了这个枚举值,那么默认向…...
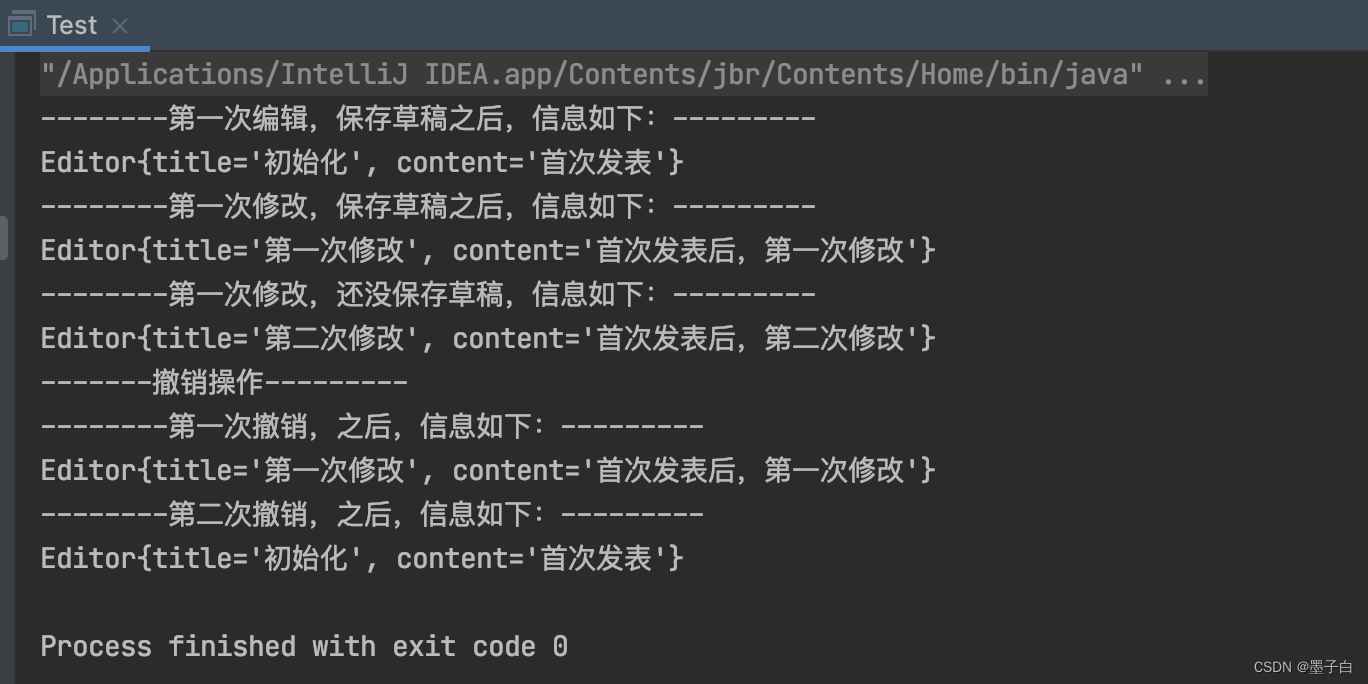
设计模式行为型——备忘录模式
目录 什么是备忘录模式 备忘录模式的实现 备忘录模式角色 备忘录模式类图 备忘录模式举例 备忘录模式代码实现 备忘录模式的特点 优点 缺点 使用场景 注意事项 实际应用 什么是备忘录模式 备忘录模式(Memento Pattern)又叫做快照模式&#x…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...

Golang——9、反射和文件操作
反射和文件操作 1、反射1.1、reflect.TypeOf()获取任意值的类型对象1.2、reflect.ValueOf()1.3、结构体反射 2、文件操作2.1、os.Open()打开文件2.2、方式一:使用Read()读取文件2.3、方式二:bufio读取文件2.4、方式三:os.ReadFile读取2.5、写…...

spring Security对RBAC及其ABAC的支持使用
RBAC (基于角色的访问控制) RBAC (Role-Based Access Control) 是 Spring Security 中最常用的权限模型,它将权限分配给角色,再将角色分配给用户。 RBAC 核心实现 1. 数据库设计 users roles permissions ------- ------…...
