数据结构—图的存储结构
6.图
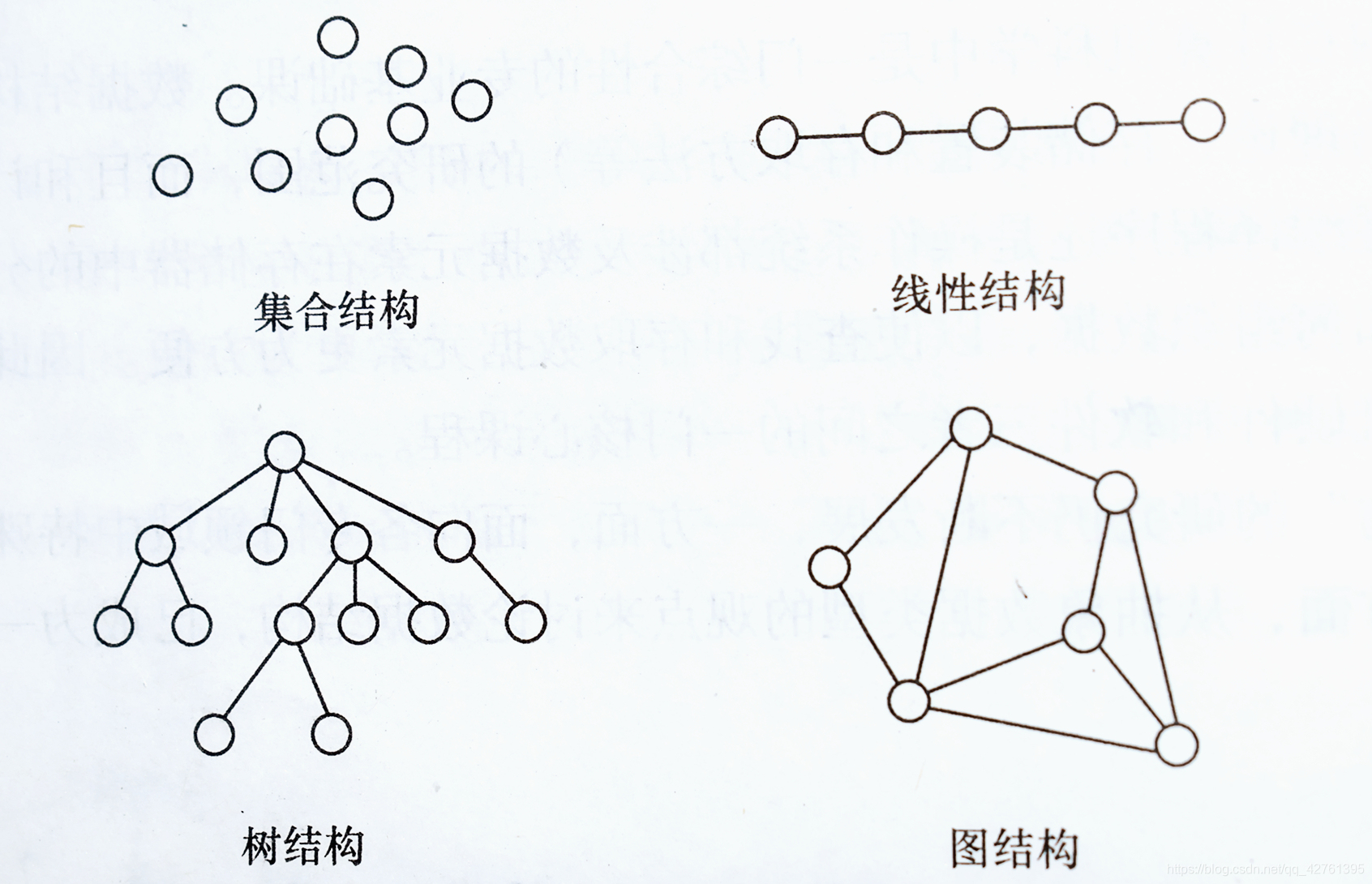
回顾:数据的逻辑结构
集合——数据元素间除 “同属于一个集合” 外,无其他关系。
线性结构——一个对一个,如线性表、栈、队列
树形结构——一个对多个,如树
图形结构——多个对多个,如图
6.1图的定义和术语
图: G=(V,E)V:顶点(数据元素)的有穷非空集合; E:边的有穷集合。
无向图:每条边都是无方向的;
有向图:每条边都是有方向的。

完全图:任意两个点都有一条边相连。
无向完全图:n 个顶点,n(n-1)/2条边
有向完全图:n 个顶点,n(n-1)条边
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-NdIzTjfy-1691238142116)(https://ts1.cn.mm.bing.net/th/id/R-C.bf9aad94a55a06758f0d0d4a2aa083bf?rik=VscqICD0R7hR%2fA&riu=http%3a%2f%2fdata.biancheng.net%2fuploads%2fallimg%2f190103%2f2-1Z103210110O8.gif&ehk=Oi7hLl6AEIQ%2f1UfWj%2fAO6riRvAKN51BTFvzwxhq%2bGSE%3d&risl=&pid=ImgRaw&r=0)]
稀疏图:有很少边或弧的图(e<nlogn)。
稠密图:有较多边或弧的图。
网:边/弧带权的图。
邻接:有边/弧相连的两个顶点之间的关系。
存在(vi,vj),则称vi和vj互为邻接点;
存在 <vi,vj>,则称vi邻接到vj,vj邻接到vi
关联(依附):边/弧与顶点之间的关系。
存在(vi,vj)/ <vi,vj>,则称该边/弧关联于vi和vj
顶点的度:与该顶点相关联的边的数目,记为TD(v)
在有向图中,顶点的度等于该顶点的入度与出度之和。
顶点v的入度是以v为顶点的有向边的条数,记作ID(v)
顶点v的出度是以v为始点的有向边的条数,记作OD(v)
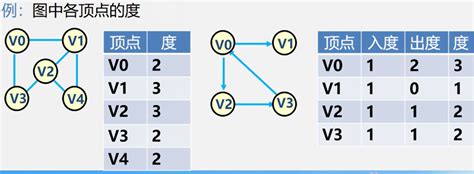
问:当有向图中仅1个顶点的入度为0,其余顶点的入度均为1,此时是何形状?
答:是树!而且是一棵有向树!
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-rztk0NIk-1691238142118)(https://ts1.cn.mm.bing.net/th/id/R-C.4f3bd2363f037cff739f8e388db9b321?rik=W0cQmZrsrYAcEA&riu=http%3a%2f%2fivr-ahnu.cn%2flectures%2fos%2fimages%2f24.jpg&ehk=rL%2blBOSUE1GCU30Sl09HWmQqTnbVhZDKEDVVUvJxi1U%3d&risl=&pid=ImgRaw&r=0)]
路径:接续的边构成的顶点序列。
路径长度:路径上边或弧的数目/权值之和。
回路(环):第一个顶点和最后一个顶点相同的路径。
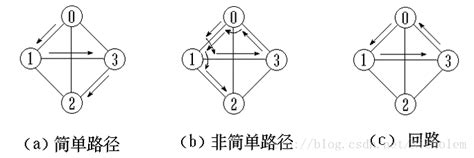
简单路径:除路径起点和终点可以相同外,其余顶点均不相同的路径。
简单回路(简单环):除路径起点和终点相同外,其余顶点均不相同的路径。
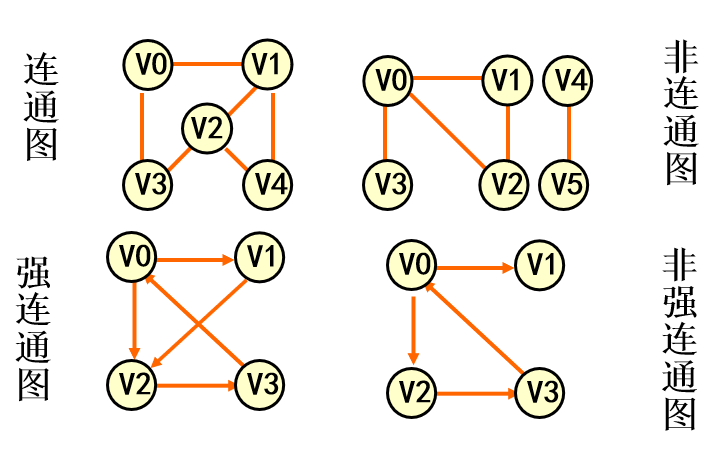
连通图(强连通图)
在无(有)向图G=(V,{E})中,若对任何两个顶点v、u都存在从v到u的路径,则称G是连通图(强连通图)。
权与网
图中边或弧所具有的相关数称为权。表明从一个顶点到另一个顶点的距离或耗费。
带权的图称为网。
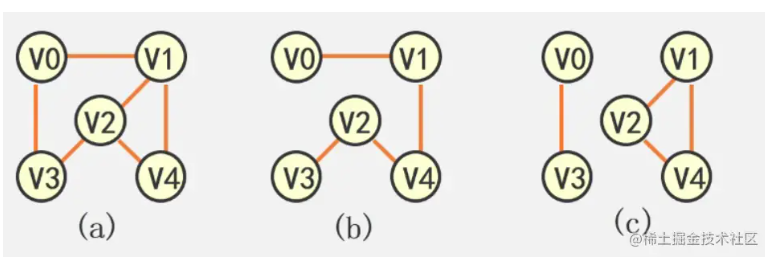
子图
设有两个图G=(V,{E})、G1=(V1,{E1}),若V1⊆V,E1⊆E,则称G1是G的子图。
例:(b),(c)是(a)的子图
连通分量(强连通分量)
-
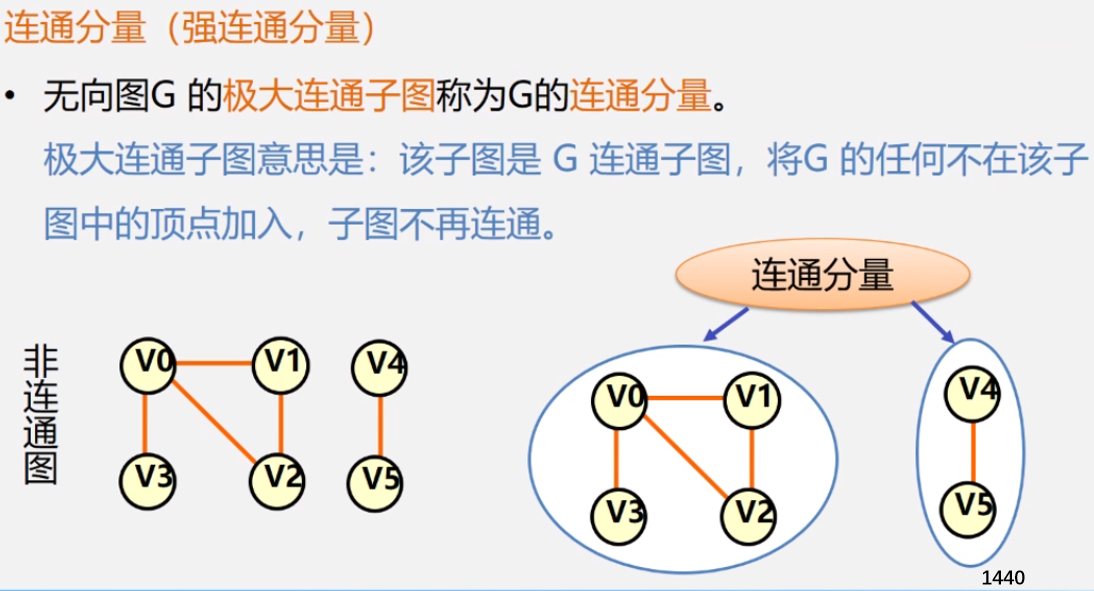
无向图G的极大连通子图称为G的连通分量。
极大连通子图意思是:该子图是G连通子图,将G的任何不在该子图中的顶点加入,子图不再连通。
-
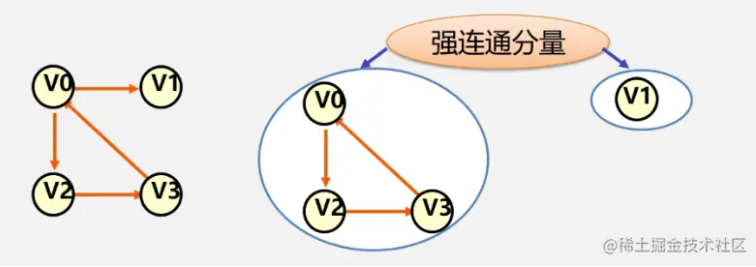
有向图G的极大强连通子图称为G的强连通分量。
极大强连通子图意思是:该子图是G的强连通子图,将D的任何不在该子图中的顶点加入,子图不再是强连通的。
-
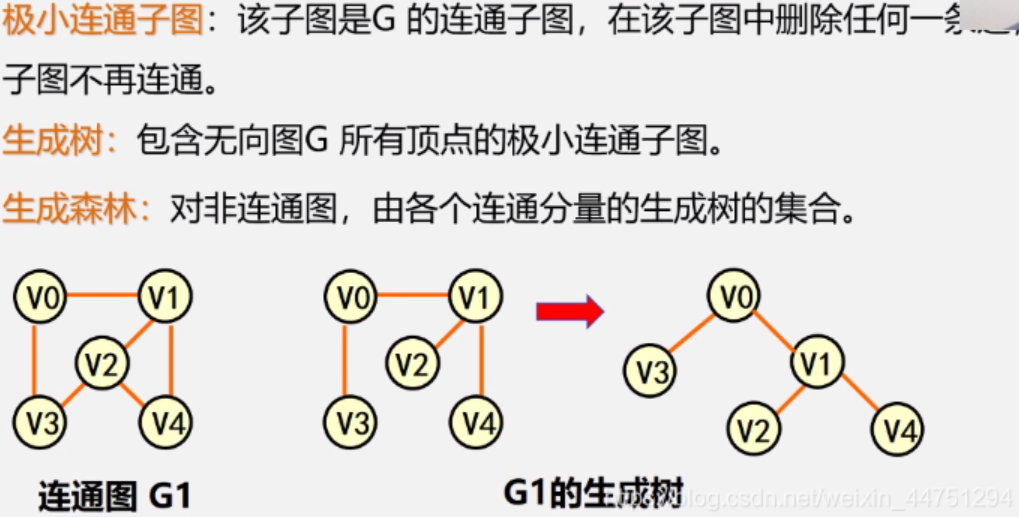
极小连通子图:该子图是G的连通子图,在该子图中删除任何一条边,子图不再连通。
-
生成树:包含无向图G所有顶点的极小连通子图。
-
生成森林:对非连通图,由各个连通分量的生成树的集合。
6.2图的存储结构
图的逻辑结构:多对多
图没有顺序存储结构,但可以借助二维数组来表示元素间的关系。
6.2.1邻接矩阵
1、数组(邻接矩阵)表示法
- 建立一个顶点表(记录各个顶点信息)和一个邻接矩阵(表示各个顶点之间关系)。
- 设图A=(V,E)有 n 个顶点。
- 图的邻接矩阵是一个二维数组。
无向图的邻接矩阵表示法
存在关系记为1,没有关系记为0
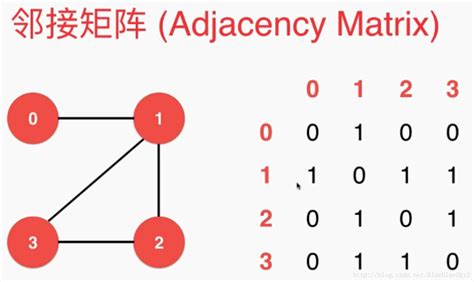
分析1:无向图的邻接矩阵是对称的。
分析2:顶点 i 的度 = 第 i 行(列)中1的个数。
特别:完全图的邻接矩阵中,对角元素为0,其余为1。
有向图的邻接矩阵表示方法
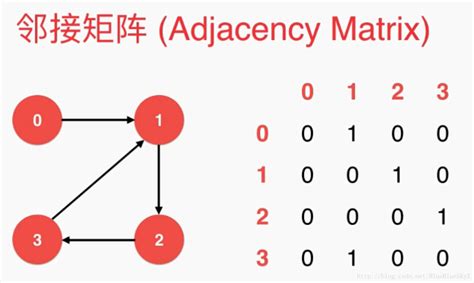
注:在有向图的邻接矩阵中,
第 i 行含义:以结点vi为尾的弧(即出度边);
第 i 列含义:以结点vi为头的弧(即入度边)。
分析1:有向图的邻接矩阵可能是不对称的。
分析2:顶点的出度 = 第i行元素之和
顶点的入度 = 第i列元素之和
顶点的度 = 第i行元素之和 + 第i列元素之和
网(即有权图)的邻接矩阵表示法
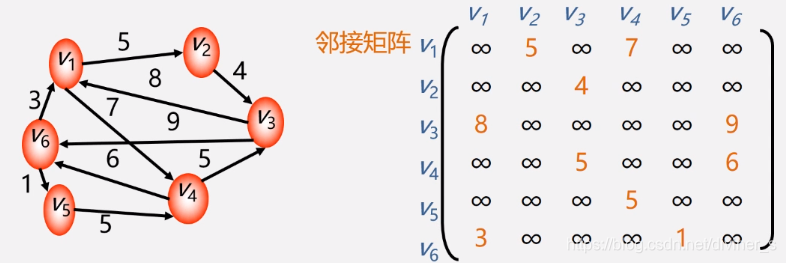
邻接矩阵存储表示,用两个数组分别存储顶点表和邻接矩阵。
#define MaxInt 32767
#define MVNum 100 //最大顶点数
typedef char VerTexType;//设顶点的数据类型为字符型
typedef int ArcType;//假设边的权值类型为整型
typedef struct{VerTexType vexs[MVNum];//顶点表ArcType arcs[MVNum][MVNum];//邻接矩阵int vexnum,arcnum;
}AMGraph;
2、采用邻接矩阵表示法创建无向网
算法思想:
- 输入总顶点数和总边数。
- 依次输入点的信息存入顶点表中。
- 初始化邻接矩阵,使每个权值初始化为最大值。
- 构造邻接矩阵。
Status CreateUDN(AMGraph &G){cin>>G.vexnum>>G.arcnum;//输入总顶点数,总边数for(i=0;i<G.vexnum;++i)cin>>G.vexs[i];//依次输入点的信息for(i=0;i<G,vexnum;++i)for(j=0;j<G.vexnum;++j)G.arcs[i][j]=MaxInt;//边的权值均设置为极大值for(k=0;k<G.arcnum;++k){cin>>v1>>v2>>w;//输入一条边所依附的顶点及边的权值i=LocateVex(G,v1);j=LocateVex(G,v2);//确定v1和v2在G中的位置G.arcs[i][j]=w;//边<v1,v2>的权值置为wG.arcs[j][i]=G.arcs[i][j];//置<v1,v2>的对称边<v2,v1>的权值为w}return OK;
}
补充算法:在图中查找顶点
int LocateVex(AMGraph G,VertexType u){int i;for(i=0;i<G.vexnum;++i)if(u==G.vexs[i]) return i;return -1;
}
3、邻接矩阵的优缺点
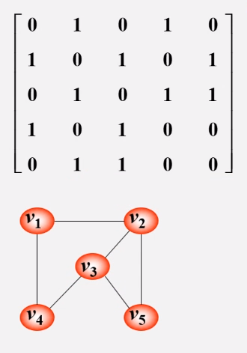
邻接矩阵有什么优点?
- 直观、简单、好理解
- 方便检查任意一对顶点间是否存在边
- 方便找任一顶点的所有“邻接点”(有边直接相连的顶点)
- 方便计算任一顶点的“度”(从该店发出的边数为“出度”,指向该点的边数为“入度”)
- 无向图:对应行(或列)非0元素的个数
- 有向图:对应行非0元素的个数是“出度”;对应列非0元素的个数是“入度”。
邻接矩阵的缺点?
-
不便于增加和删除顶点
-
浪费空间——存稀疏图(点很多而边很少)有大量无效元素
——对稠密图(特别是完全图)还是很合算的
-
浪费时间——统计稀疏图中一共有多少条边。
6.2.2邻接表
1、邻接表表示法(链式)
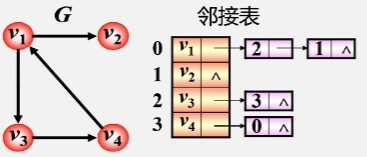
- 顶点:按编号顺序将顶点数据存储在一维数组中;
- 关联同一顶点的边(以顶点为尾的弧):用线性链表存储
无向图邻接表
特点:
-
邻接表不唯一
-
若无向图中有n个顶点,e条边,则其邻接表需n个头结点和2e个表结点。适宜存储稀疏图。
-
无向图中顶点的度为第i个单链表中的结点数。
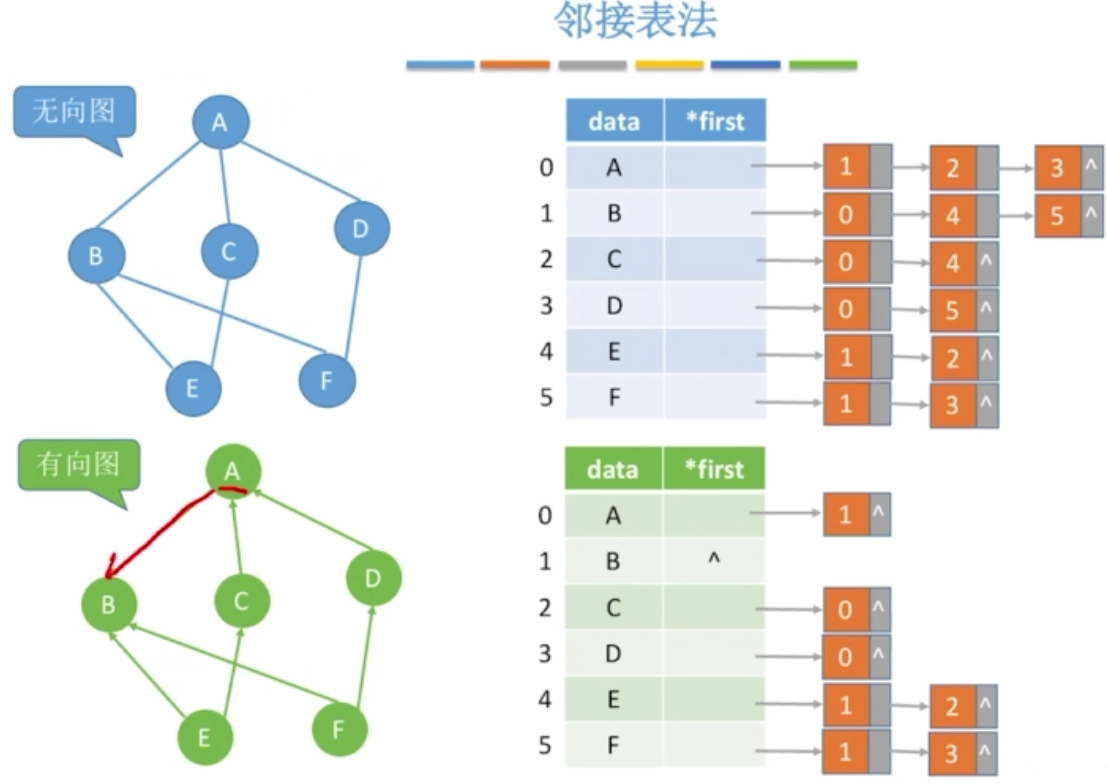
有向图邻接表
特点:找出度易,找入度难
- 顶点的出度就是第i个单链表中的结点个数。
- 顶点的入度为整个单链表中邻接点域值是i-1的结点个数。
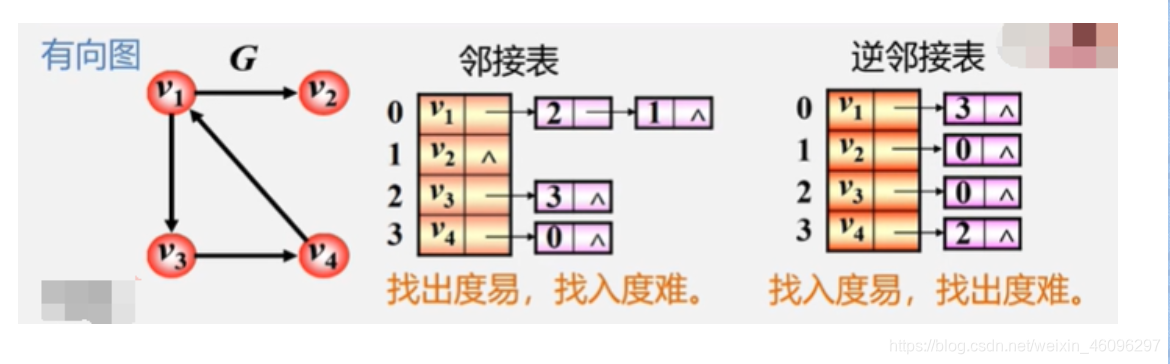
图的邻接表存储表示
顶点的结点结构
typedef struct VNode{VerTexType data;//顶点信息ArcNode *firstarc;//指向第一条依附该顶点的边的指针
}VNode,AdjList[MVNum];//AdjList表示邻接表类型
说明:例如,AdjList v; 相当于:VNode v[MVNum];
弧(边)的结点结构
#define MVNum 100
typedef struct ArcNode{//边结点int adjvex;//该边所指向的顶点的位置struct ArcNode *nextarc;//指向下一条边的指针OtherInfo info;//和边相关的信息
}ArcNode;
图的结构定义
typedef struct{AdjList vertices;int vexnum,arcnum;//图的当前顶点数和弧数
}ALGraph;
2、采用邻接表创建无向网
算法思想:
-
输入总顶点数和总边数
-
建立顶点表
依次输入点的信息存入顶点表中
使每个表头结点的指针域初始化为NULL
-
创建邻接表
依次输入每条边依附的两个顶点
确定两个顶点的序号i和j,建立边结点
将此边结点分别插入到vi和vj对应的两个边链表的头部
Status CreateUDG(ALGraph &G){cin>>G.vexnum>>G.arcnum;//输入总顶点数,总边数for(i=0;i<G.vexnum;++i){//输入各点,构造表头结点表cin>>G.vertices[i].data;//输入顶点值G.vertices[i].firstarc=NULL;//初始化表头结点的指针域}for(k=0;k<G.arcnum;++k){//输入各边,构造邻接表cin>>v1>>v2;//输入一条边依附的两个顶点i=LocateVex(G,v1);j=LocateVex(G.v2);p1=new ArcNode;//生成一个新的边结点*p1p1->adjvex=j;//邻接点序号为jpi->nextarc=G.vertices[i].firstarc;G.vertices[i].firstarc=p1;//将新结点*p1插入顶点vi的边表头部p2=new ArcNode;//生成另一个对称的新的边结点p2->adjvex=i;p2->nextarc=G.vertices[j].firstarc;G.vertices[j].firstarc=p2;//将新结点*p2插入顶点vj的边表头部}return OK;
}
3、邻接表特点
-
方便找任一顶点的所有“邻接点”
-
节约稀疏图的空间
- 需要N个头指针 + 2E个结点(每个结点至少2个域)
-
方便计算任一顶点的“度”
- 对无向图:是的
- 对有向图:只能计算“出度”;需要构造“逆邻接表”(纯指向自己的边)来方便计算“入度”
-
不方便检查任意一对顶点间是否存在边
6.2.3邻接矩阵与邻接表的关系
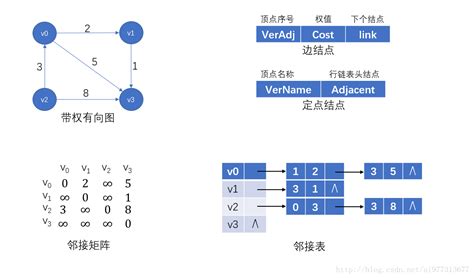
联系:邻接表中每个链表对应与邻接矩阵中的一行,链表中结点个数等于一行中非零元素的个数。
区别:
- 对于任一确定的无向图,邻接矩阵是唯一的(行列号与顶点编号一致),当邻接表不唯一(链接次序与顶点编号无关)。
- 邻接矩阵的空间复杂度为O(n2),而邻接表的空间复杂度为O(n+e)。
用途:邻接矩阵多用于稠密图;而邻接表多用于稀疏图。
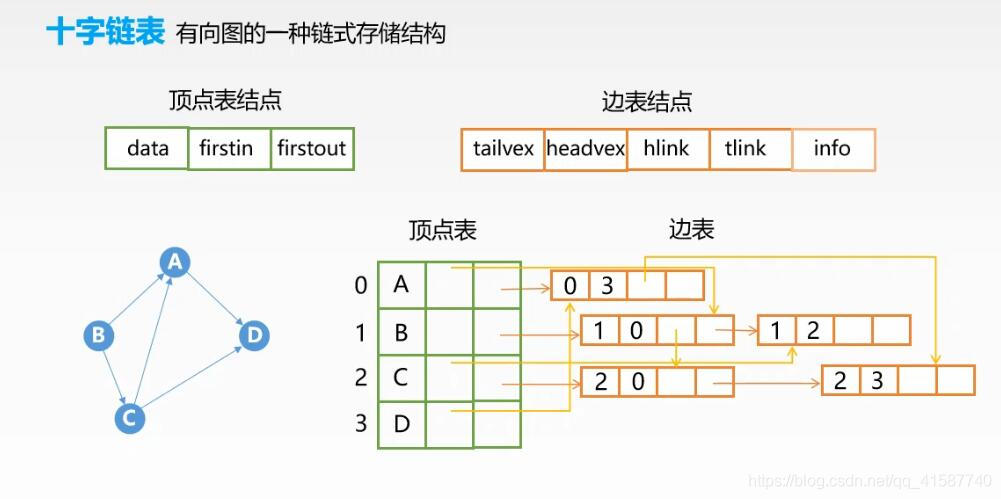
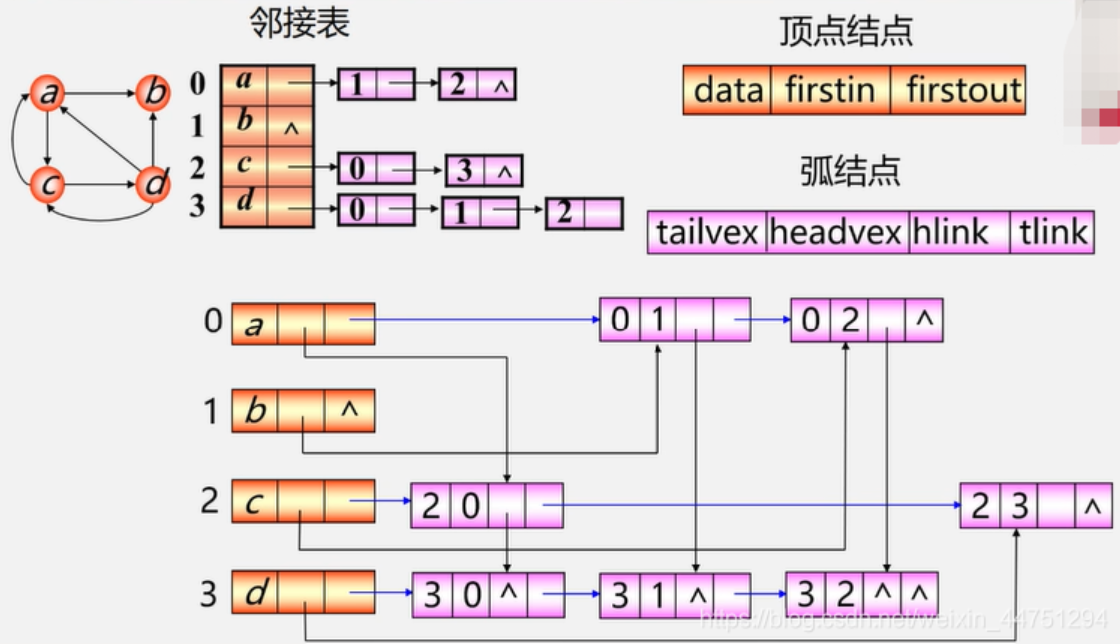
6.2.4十字链表
十字链表是有向图的另一种链式存储结构。我们也可以把她看成是将有向图的邻接表和逆邻接表结合起来形成的一种链表。
有向图中的每一条弧对应十字链表中的一个弧结点,同时有向图中的每个顶点在十字链表中对应有一个结点,叫做顶点结点。
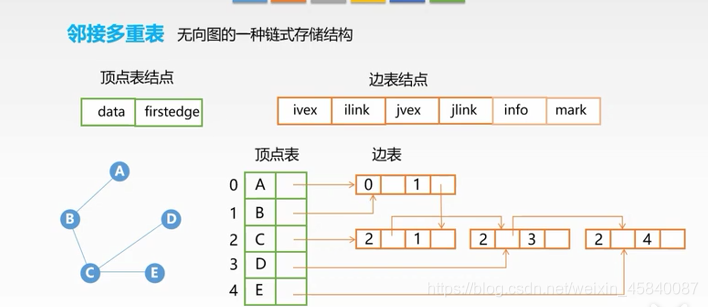
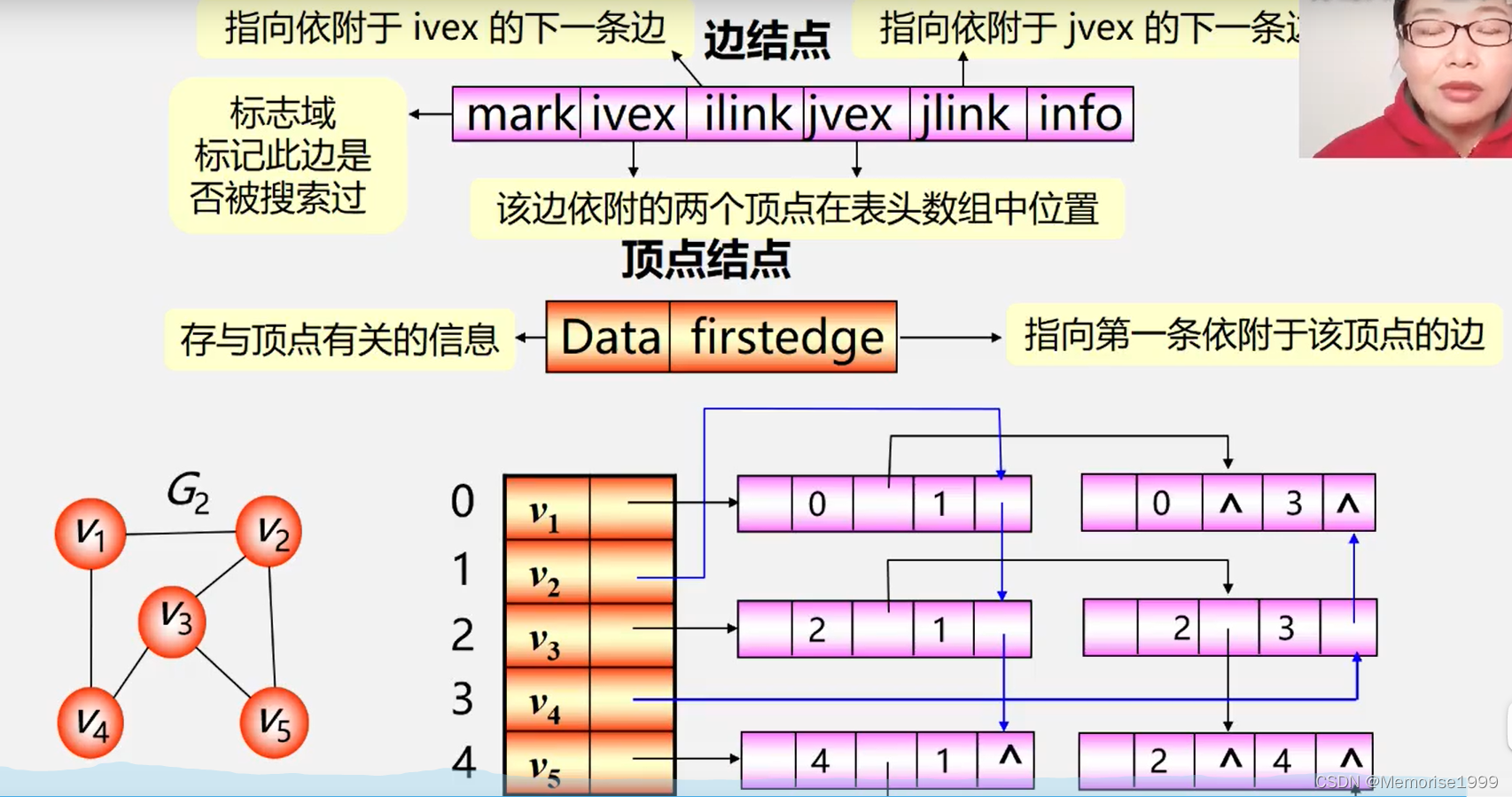
6.2.5邻接多重表
邻接表优点:容易求得顶点和边的信息。
缺点:某些操作不方便(如:删除一条边需找表示此边的两个结点)。
邻接表中,任何一条边,都会出现两次
相关文章:

数据结构—图的存储结构
6.图 回顾:数据的逻辑结构 集合——数据元素间除 “同属于一个集合” 外,无其他关系。 线性结构——一个对一个,如线性表、栈、队列 树形结构——一个对多个,如树 图形结构——多个对多个,如图 6.1图的定义和术语 图:…...

Vue3 中 setup,ref 和 reactive 的理解
setup Vue3中使用了Composition API这种写法,使得所有的组合API函数都在此使用, 只在初始化时执行一次。 函数如果返回对象, 对象中的属性或方法, 模板中可以直接使用 ref 作用:定义一个数据的响应式 语法:const xxx ref(initValue) 一般用来…...

BL302嵌入式ARM控制器进行SQLite3数据库操作的实例演示
本文主要讲述了在钡铼技术BL302嵌入式arm控制器上运行 SQLite3 数据库的命令示例。SQLite3 是一个轻型的嵌入式数据库,不需要安装数据库服务器进程,占用资源低且处理速度快。 首先,需要将对应版本的 SQLite3 文件复制到设备的 /usr/ 目录下&…...
C++ 多线程:std::future
std::future std::future 简介示例1博客引用来源 std::future 简介 我们前面介绍的std::thread 是C11中提供异步创建多线程的工具,只能是异步运行任务,却无法获取任务执行的结果,一般都是依靠全局对象,全局对象在多线程下是及其不…...
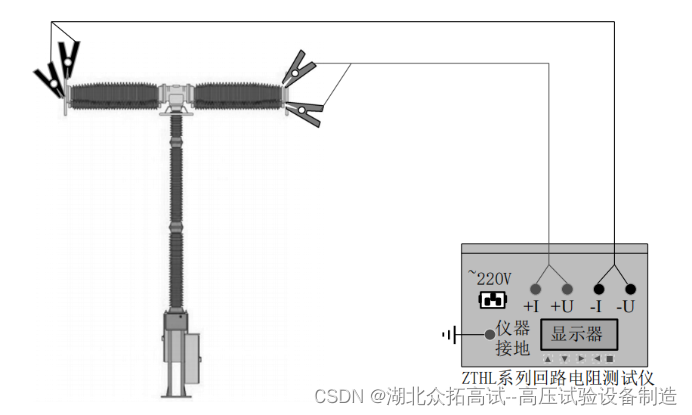
断路器回路电阻试验
试验目的 断路器回路电阻主要取决于断路器动、 静触头的接触电阻, 其大小直接影响正常 运行时的发热情况及切断短路电流的性能, 是反应安装检修质量的重要数据。 试验设备 回路电阻测试仪 厂家: 湖北众拓高试代销 试验接线 对于单断口的断路器, 通过断口两端的接线…...

Python中的CALL_FUNCTION指令
在Python字节码中,CALL_FUNCTION指令后跟的数字代表这次函数调用需要从栈上取出的参数的数量。具体来说,这个数字包括位置参数和关键字参数的数量。 这个数字的低两位表示位置参数的数量,然后每两位表示一个关键字参数的数量。因此ÿ…...
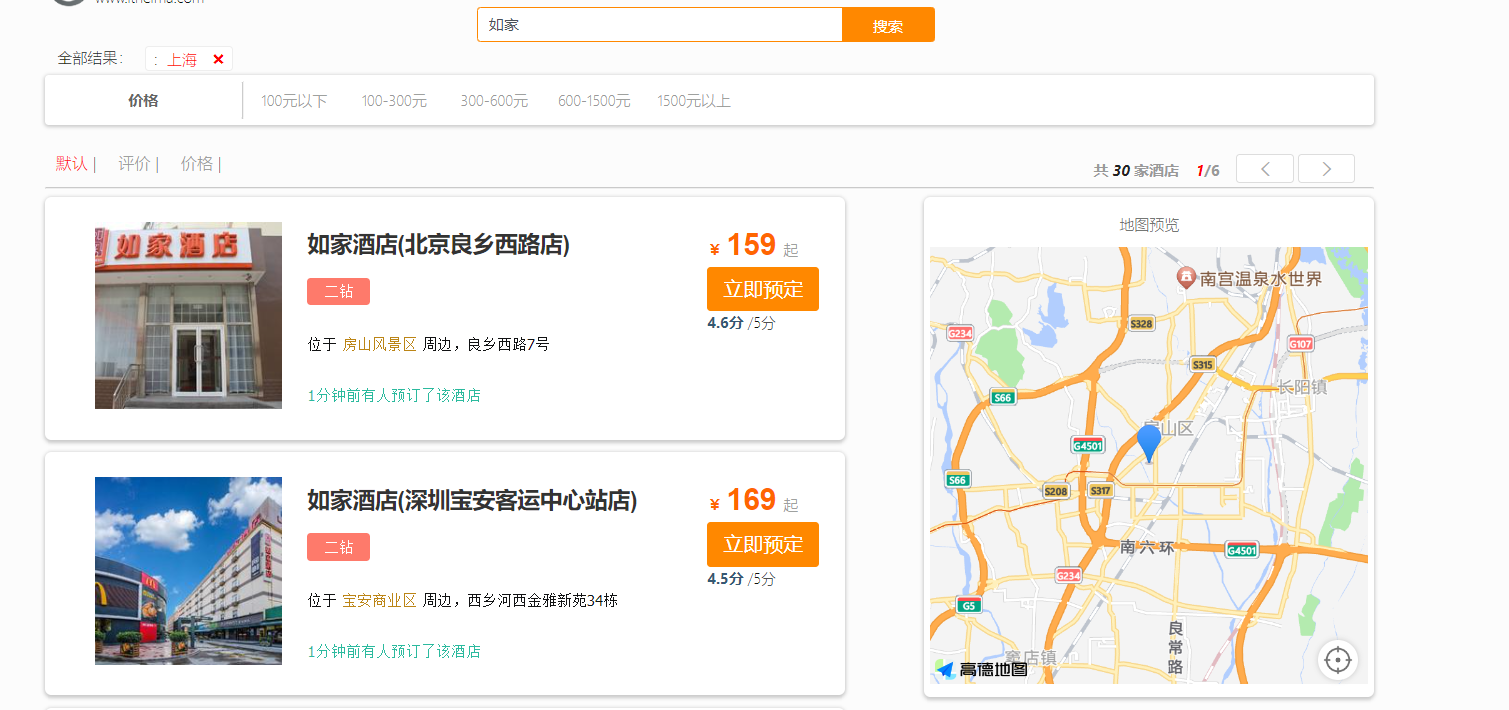
微服务——es数据聚合+RestClient实现聚合
数据聚合 聚合的种类 DSL实现Bucket聚合 如图所示,设置了10个桶,那么就显示了数量最多的前10个桶,品牌含有7天酒店的有30家, 品牌含有如家的也有30家。 修改排序规则 限定聚合范围 DSL实现Metrics聚合 如下案例要求对不同的品…...
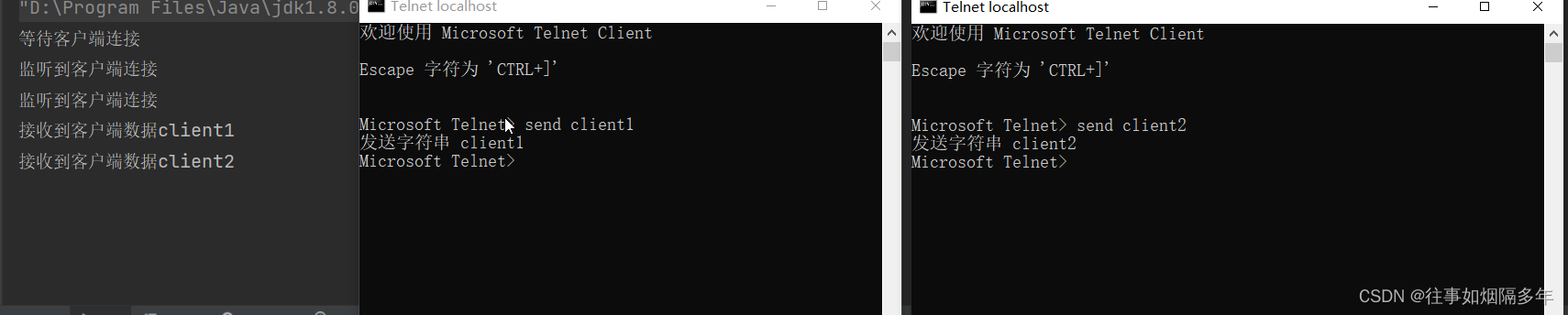
代码分析Java中的BIO与NIO
开发环境 OS:Win10(需要开启telnet服务,或使用第三方远程工具) Java版本:8 BIO 概念 BIO(Block IO),即同步阻塞IO,特点为当客户端发起请求后,在服务端未处理完该请求之前ÿ…...
网络安全(黑客)工作篇
一、网络安全行业的就业前景如何? 网络安全行业的就业前景非常广阔和有吸引力。随着数字化、云计算、物联网和人工智能等技术的迅速发展,网络安全的需求持续增长。以下是网络安全行业就业前景的一些关键因素: 高需求:随着互联网的…...
zookeeper入门学习
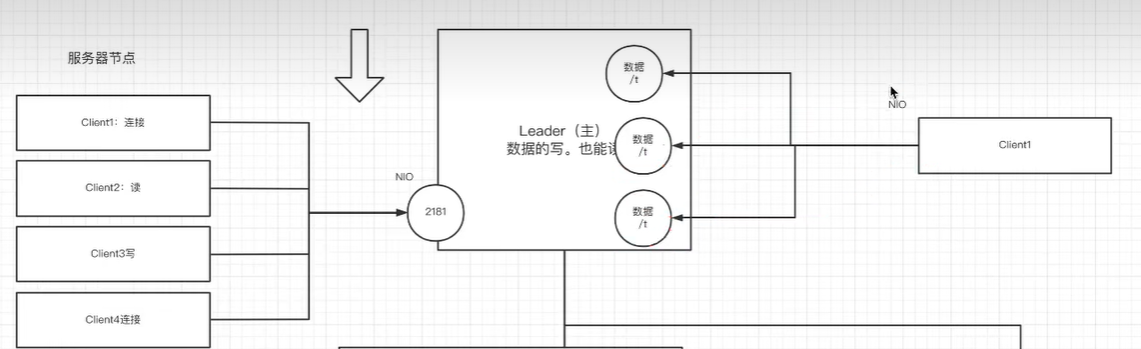
zookeeper入门学习 zookeeper应用场景 分布式协调组件 客户端第一次请求发给服务器2,将flag值修改为false,第二次请求被负载均衡到服务器1,访问到的flag也会是false 一旦有节点发生改变,就会通知所有监听方改变自己的值&#…...

VirtualEnv 20.24.0 发布
导读VirtualEnv 20.24.0 现已发布,VirtualEnv 用于在一台机器上创建多个独立的 Python 运行环境,可隔离项目之间的第三方包依赖,为部署应用提供方便,把开发环境的虚拟环境打包到生产环境即可,不需要在服务器上再折腾一…...
LabVIEW开发高压航空航天动力系统爬电距离的测试
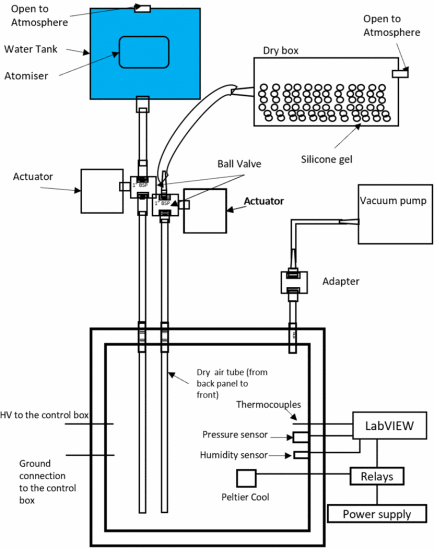
LabVIEW开发高压航空航天动力系统爬电距离的测试 更多电动飞机MEA技术将发电,配电和用电集成到一个统一的系统中,提高了飞机的可靠性和可维护性。更多的电动飞机使用更多的电能来用电动替代品取代液压和气动系统。对车载电力的需求不断增加,…...
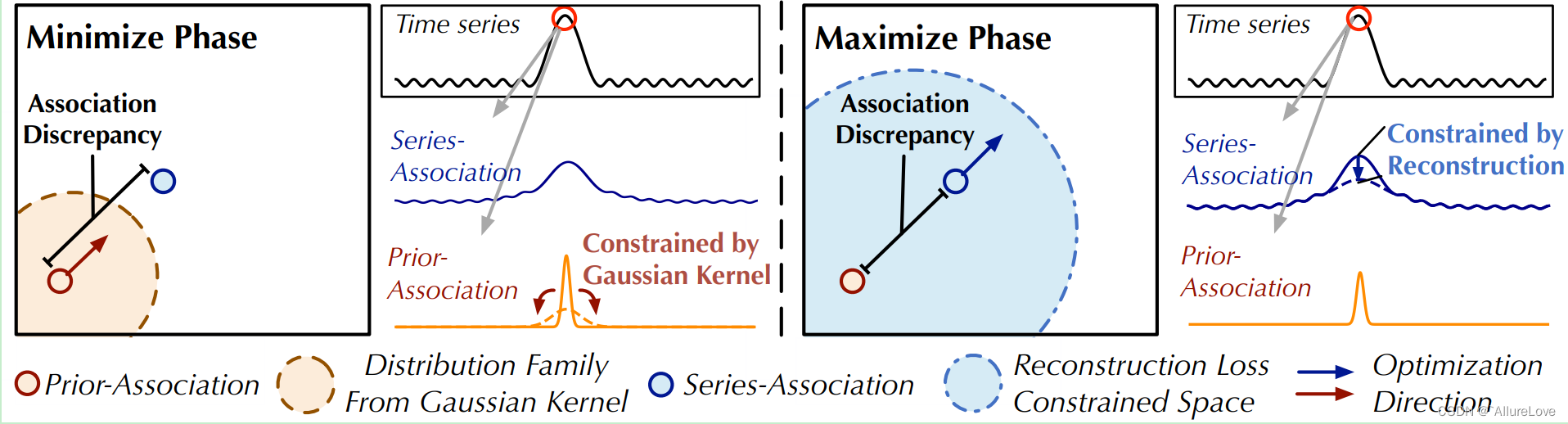
【论文阅读】基于深度学习的时序异常检测——Anomaly Transformer
系列文章链接 数据基础:多维时序数据集简介 论文一:2022 Anomaly Transformer:异常分数预测 论文二:2022 TransAD:异常分数预测 论文链接:Anomaly Transformer.pdf 代码链接:https://github.co…...

Java并发总结
1.创建线程三种方式 Runnable.Callable接口使用继承Thread类的方式创建多线程Runnable 和Callable区别 Callable规定(重写)的方法是call(),Runnable规定(重写)的方法是run()。Callable的任务执行后可返回值࿰…...
视频汇聚平台EasyCVR视频广场侧边栏支持拖拽
为了提升用户体验以及让平台的操作更加符合用户使用习惯,我们在EasyCVR v3.3版本中,支持面包屑侧边栏的广场视频、分组列表、收藏这三个模块拖拽排序,并且该操作在视频广场、视频调阅、电子地图、录像回放等页面均能支持。 TSINGSEE青犀视频…...

MyCat分片规则——范围分片、取模分片、一致性hash、枚举分片
1.范围分片 2.取模分片 范围分片和取模分片针对数字类型的字段可以,但是针对于字符串类型的字段时。这两种就不适用了。 3.一致性hash 4.枚举分片 默认节点指的是,如果我们向数据库表插入数据的时候,超出了这个枚举值,那么默认向…...
设计模式行为型——备忘录模式
目录 什么是备忘录模式 备忘录模式的实现 备忘录模式角色 备忘录模式类图 备忘录模式举例 备忘录模式代码实现 备忘录模式的特点 优点 缺点 使用场景 注意事项 实际应用 什么是备忘录模式 备忘录模式(Memento Pattern)又叫做快照模式&#x…...
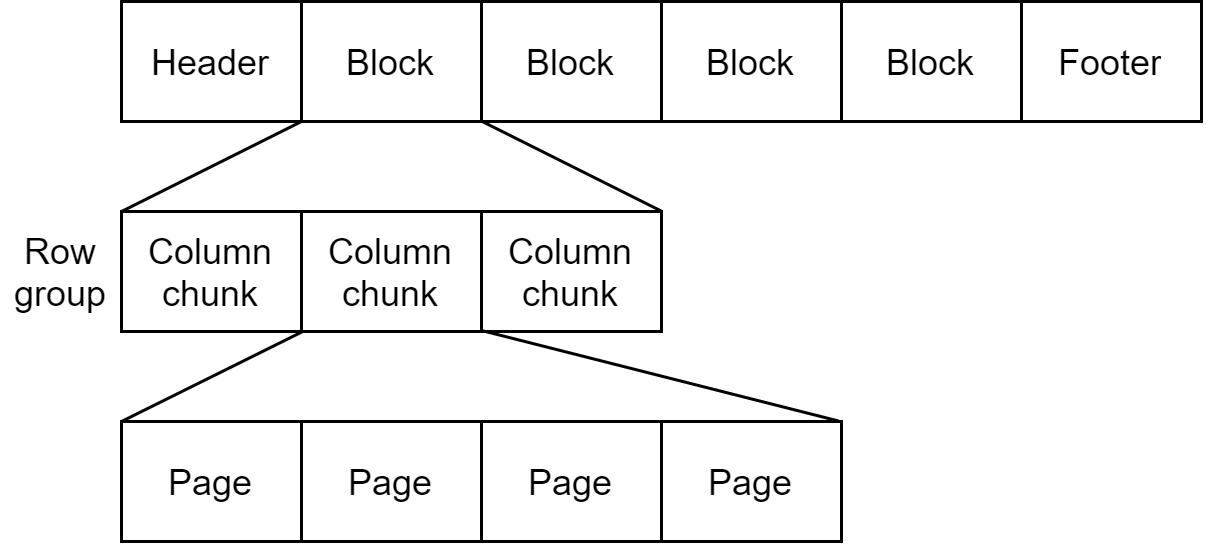
Parquet存储的数据模型以及文件格式
文章目录 数据模型Parquet 的原子类型Parquet 的逻辑类型嵌套编码 Parquet文件格式 本文主要参考文献:Tom White. Hadoop权威指南. 第4版. 清华大学出版社, 2017.pages 363. Aapche Parquet是一种能有效存储嵌套数据的列式存储格式,在Spark中应用较多。 …...

Go和Java实现访问者模式
Go和Java实现访问者模式 我们下面通过一个解压和压缩各种类型的文件的案例来说明访问者模式的使用。 1、访问者模式 在访问者模式中,我们使用了一个访问者类,它改变了元素类的执行算法。通过这种方式,元素的执行算法可以随 着访问者改变而…...

想要通过软件测试的面试,都需要学习哪些知识
很多人认为,软件测试是一个简单的职位,职业生涯走向也不会太好,但是随着时间的推移,软件测试行业的变化,人们开始对软件测试行业的认知有了新的高度,越来越多的人开始关注这个行业,开始重视这个…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...

论文阅读笔记——Muffin: Testing Deep Learning Libraries via Neural Architecture Fuzzing
Muffin 论文 现有方法 CRADLE 和 LEMON,依赖模型推理阶段输出进行差分测试,但在训练阶段是不可行的,因为训练阶段直到最后才有固定输出,中间过程是不断变化的。API 库覆盖低,因为各个 API 都是在各种具体场景下使用。…...

ui框架-文件列表展示
ui框架-文件列表展示 介绍 UI框架的文件列表展示组件,可以展示文件夹,支持列表展示和图标展示模式。组件提供了丰富的功能和可配置选项,适用于文件管理、文件上传等场景。 功能特性 支持列表模式和网格模式的切换展示支持文件和文件夹的层…...

Vue3 PC端 UI组件库我更推荐Naive UI
一、Vue3生态现状与UI库选择的重要性 随着Vue3的稳定发布和Composition API的广泛采用,前端开发者面临着UI组件库的重新选择。一个好的UI库不仅能提升开发效率,还能确保项目的长期可维护性。本文将对比三大主流Vue3 UI库(Naive UI、Element …...

【java面试】微服务篇
【java面试】微服务篇 一、总体框架二、Springcloud(一)Springcloud五大组件(二)服务注册和发现1、Eureka2、Nacos (三)负载均衡1、Ribbon负载均衡流程2、Ribbon负载均衡策略3、自定义负载均衡策略4、总结 …...
EasyRTC音视频实时通话功能在WebRTC与智能硬件整合中的应用与优势
一、WebRTC与智能硬件整合趋势 随着物联网和实时通信需求的爆发式增长,WebRTC作为开源实时通信技术,为浏览器与移动应用提供免插件的音视频通信能力,在智能硬件领域的融合应用已成必然趋势。智能硬件不再局限于单一功能,对实时…...