[LeetCode 1237]找出给定方程的正整数解
题目描述
题目链接:[LeetCode 1237]找出给定方程的正整数解
给你一个函数 f(x, y) 和一个目标结果 z,函数公式未知,请你计算方程 f(x,y) == z 所有可能的正整数 数对 x 和 y。满足条件的结果数对可以按任意顺序返回。
尽管函数的具体式子未知,但它是单调递增函数,也就是说:
- f(x, y) < f(x + 1, y)
- f(x, y) < f(x, y + 1)
函数接口定义如下:
interface CustomFunction {
public:// Returns some positive integer f(x, y) for two positive integers x and y based on a formula.int f(int x, int y);
};
你的解决方案将按如下规则进行评判:
- 判题程序有一个由 CustomFunction 的 9 种实现组成的列表,以及一种为特定的 z 生成所有有效数对的答案的方法。
- 判题程序接受两个输入:function_id(决定使用哪种实现测试你的代码)以及目标结果 z 。
- 判题程序将会调用你实现的 findSolution 并将你的结果与答案进行比较。
- 如果你的结果与答案相符,那么解决方案将被视作正确答案,即 Accepted 。
示例1
输入:function_id = 1, z = 5
输出:[[1,4],[2,3],[3,2],[4,1]]
解释:function_id = 1 暗含的函数式子为 f(x, y) = x + y
以下 x 和 y 满足 f(x, y) 等于 5:
x=1, y=4 -> f(1, 4) = 1 + 4 = 5
x=2, y=3 -> f(2, 3) = 2 + 3 = 5
x=3, y=2 -> f(3, 2) = 3 + 2 = 5
x=4, y=1 -> f(4, 1) = 4 + 1 = 5
示例2
输入:function_id = 2, z = 5
输出:[[1,5],[5,1]]
解释:function_id = 2 暗含的函数式子为 f(x, y) = x * y
以下 x 和 y 满足 f(x, y) 等于 5:
x=1, y=5 -> f(1, 5) = 1 * 5 = 5
x=5, y=1 -> f(5, 1) = 5 * 1 = 5
提示
- 1 <= function_id <= 9
- 1 <= z <= 100
- 题目保证 f(x, y) == z 的解处于 1 <= x, y <= 1000 的范围内。
- 在 1 <= x, y <= 1000 的前提下,题目保证 f(x, y) 是一个 32 位有符号整数。
思路分析
1.题目描述很不清晰,尤其是引入这个function_id
完全可以不用管这个function_id,其实就是告诉你我有九个这样的函数,函数都具有单调递增的性质,那我管你几个函数,只需要知道函数的性质就好了!
2.x,y都为1000,问题规模卡在n^2级别,看到单调,第一反应想到的就是二分
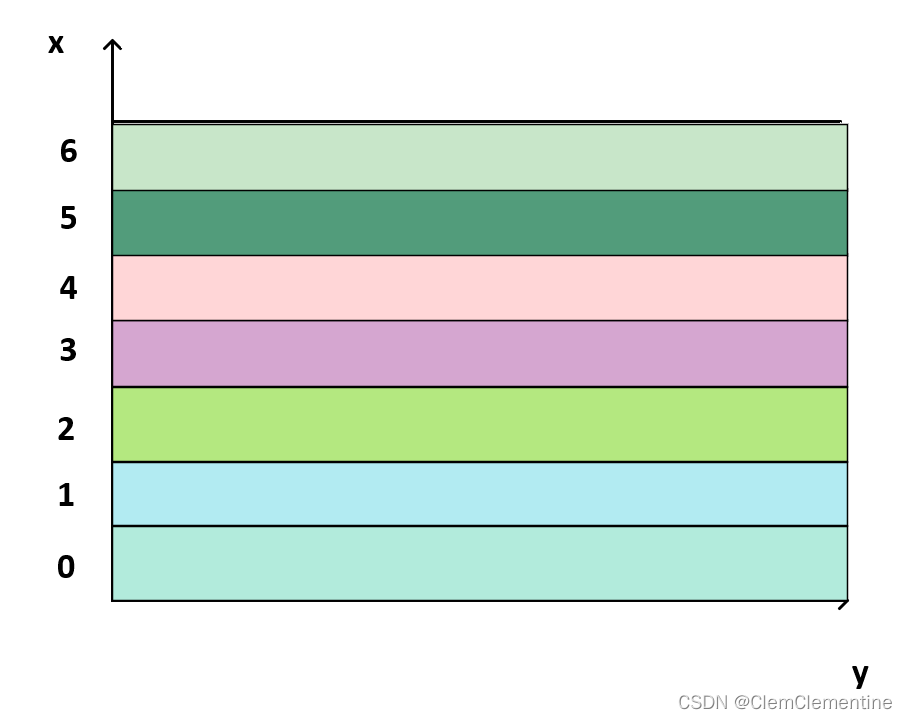
3.但是对于两个维度x和y来说很麻烦,所以我们可以固定一个维度,从这个维度上看,就是一个一维的单调递增函数,如图所示:固定住x,比如x=0,那么这个维度上,y就是单调递增的,所以可以通过枚举x,然后在每个维度上二分y来做,复杂度是O(nlogn) < O(n2n^2n2)
代码
class Solution {
public:vector<vector<int>> findSolution(CustomFunction& c, int z) {vector<vector<int>> res;//遍历xfor (int x = 1; x <= 1000; x++) {//二分yint l = 1, r = 1000;while(l < r) {int mid = (l + r) >> 1;if(c.f(x, mid) >= z) r = mid;else l = mid + 1;}//如果二分出来的点是零点,那么保存答案if(c.f(x, l) == z) res.push_back({x, l});}return res;}
};
相关文章:

[LeetCode 1237]找出给定方程的正整数解
题目描述 题目链接:[LeetCode 1237]找出给定方程的正整数解 给你一个函数 f(x, y) 和一个目标结果 z,函数公式未知,请你计算方程 f(x,y) z 所有可能的正整数 数对 x 和 y。满足条件的结果数对可以按任意顺序返回。 尽管函数的具体式子未知…...
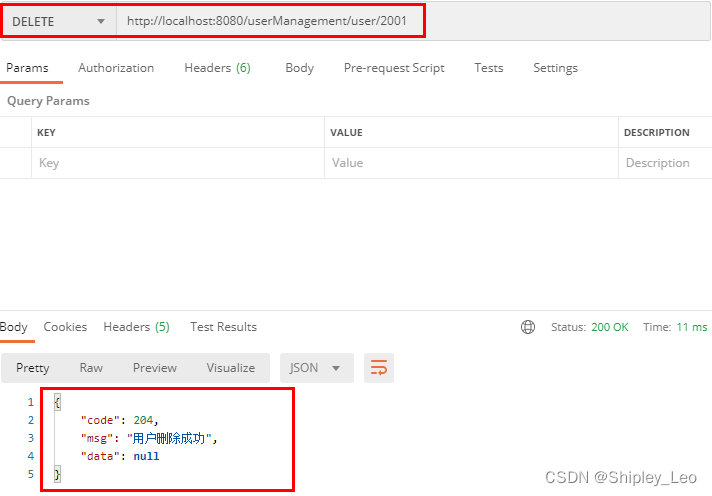
6.2 构建 RESTful 应用接口
第6章 构建 RESTful 服务 6.1 RESTful 简介 6.2 构建 RESTful 应用接口 6.3 使用 Swagger 生成 Web API 文档 6.4 实战:实现 Web API 版本控制 6.2 构建 RESTful 应用接口 6.2.1 Spring Boot 对 RESTful 的支持 Spring Boot 提供的spring-boot-starter-web组件完全…...

20230218英语学习
How Italian Artist’s Mild Colors Dominate World of Design 温柔的“莫兰迪色”,如何引领设计时尚? The Morandi color scheme has become an across-the-board fashion that now prevails in the world of design.Soft and sophisticated Morandi c…...

Linux单一服务管理systemctl
基本上systemd这个启动服务机制只有systemctl命令来处理,所以全部的操作都需要使用systemctl systemctl管理单一服务 一般来说服务的启动有两个阶段,一个是开机是否启动,以及现在是否启动 systemctl【command】【unit】 command主要有&…...
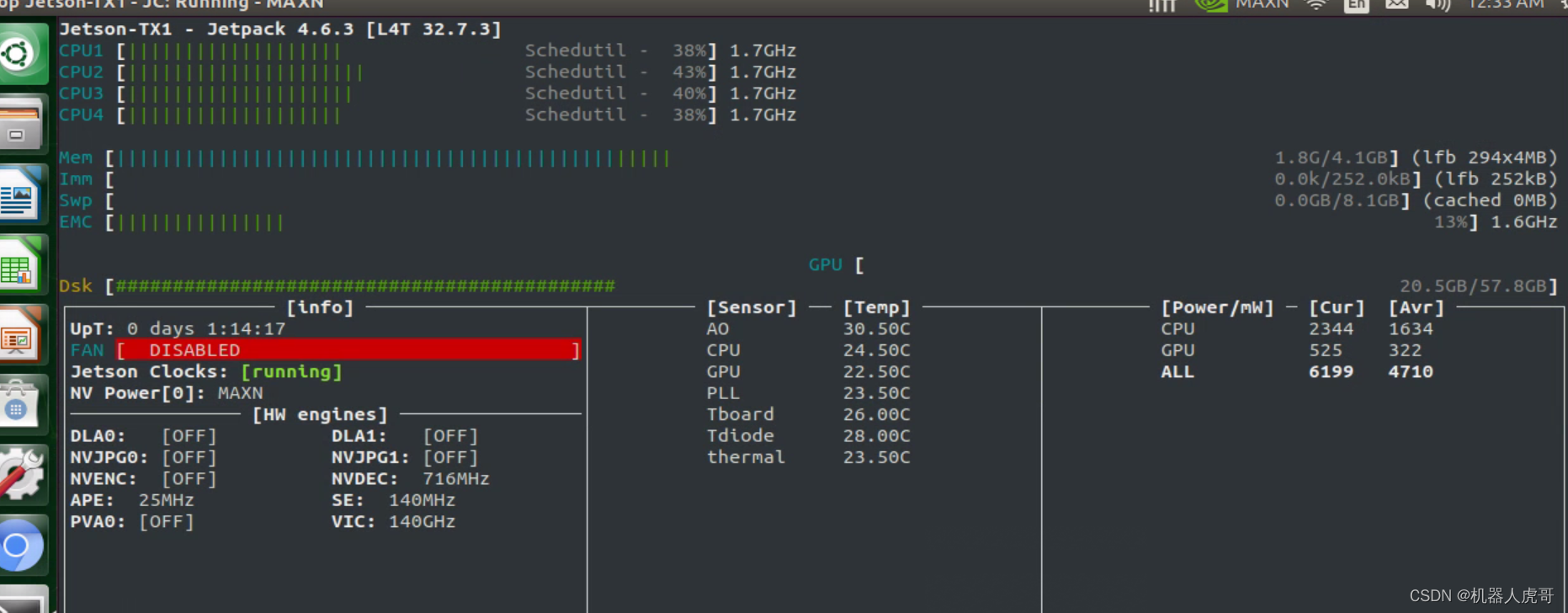
【GStreamer 】 TX1中CPU和GPU解码显示海康相机RTSP流
大家好,我是虎哥,今天找了一套海康的相机,想后续测试一下DeepStream用网络相机RTSP流做输入看看后续目标识别和分类。但是还是想先实时看看视频,当然,可以选择VLC去查看,顺道我也用GStreamer 来测试了一下&…...

匿名内部类、Lambda表达式、方法引用对比分析
文章目录一、匿名内部类1. 语法格式2. 使用方法① 传统方式② 匿名内部类方式二、Lambda表达式1. 语法格式2. 使用方法① 匿名内部类方式② Lambda表达式方式三、方法引用1. 语法格式2. 使用方法① 类型的静态方法引用② 类型的构造方法引用③ 类型的实例方法引用④ 对象的实例…...
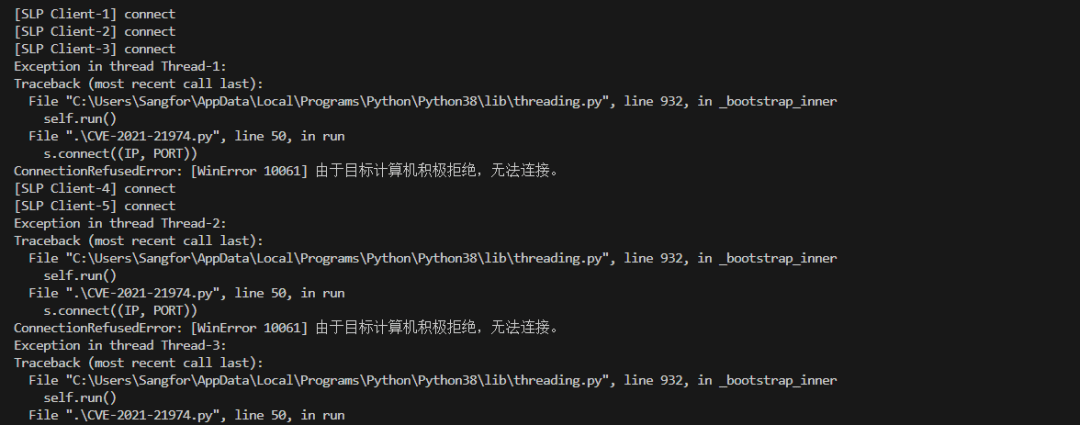
ESXi主机CVE-2021-21972漏洞复现安全处置建议
一、漏洞简介 vSphere 是 VMware 推出的虚拟化平台套件,包含 ESXi、vCenter Server 等一系列的软件。其中 vCenter Server 为 ESXi 的控制中心,可从单一控制点统一管理数据中心的所有 vSphere 主机和虚拟机。 vSphere Client(HTML5…...

研报精选230217
目录 【行业230217毕马威】奢侈品行业新气象【行业230217国信证券】医药生物行业2023年2月投资策略:持续关注疫后复苏和创新两大主线【行业230217国金证券】航空锻造:稳定格局筑专业化壁垒,顺势而为拓产业链深度【个股230217西南证券_招商轮船…...
(std::unordered_set)(一))
c++11 标准模板(STL)(std::unordered_set)(一)
定义于头文件 <unordered_set> template< class Key, class Hash std::hash<Key>, class KeyEqual std::equal_to<Key>, class Allocator std::allocator<Key> > class unordered_set;(1)(C11 起)namespace pmr { templ…...

【C语言进阶】你听说过柔性数组吗?
👦个人主页:Weraphael ✍🏻作者简介:目前是C语言学习者 ✈️专栏:C语言航路 🐋 希望大家多多支持,咱一起进步!😁 如果文章对你有帮助的话 欢迎 评论💬 点赞&a…...

[LeetCode]1237. 找出给定方程的正整数解
题目链接:https://leetcode.cn/problems/find-positive-integer-solution-for-a-given-equation/description/ 题目描述: 样例1: 输入:function_id 1, z 5 输出:[[1,4],[2,3],[3,2],[4,1]] 解释:functi…...

【路径规划】基于A*算法和Dijkstra算法的路径规划(Python代码实现)
👨🎓个人主页:研学社的博客💥💥💞💞欢迎来到本博客❤️❤️💥💥🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密…...

蓝桥杯 stm32 PWM 设置占空比
本文代码使用 HAL 库。 文章目录 前言一、创建CubeMX 工程 ,占空比分析:二、相关函数:1. 获取 CNT函数2.设置CNT为 0 函数(计算器清零)3.开启TIM2_CH1的输入捕获中断函数4.TIM 回调函数三、设置上升沿,下降沿四、在lcd上显示 R40 占空比 详细代码五、设置占空比,输出 PW…...
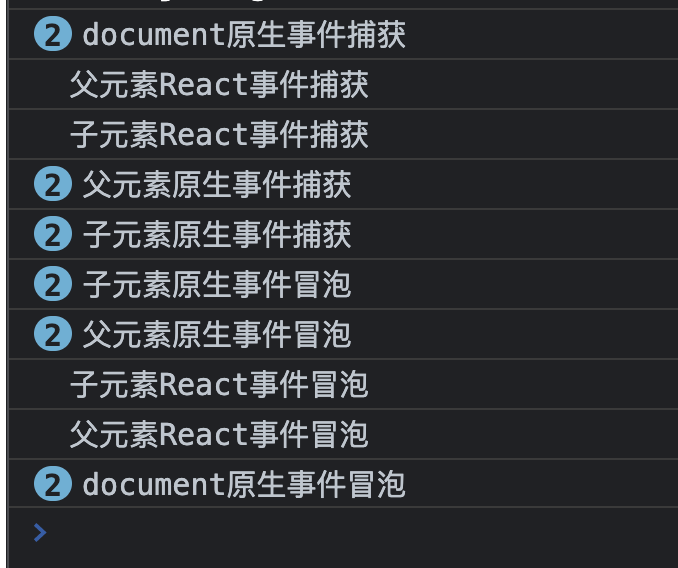
React 合成事件理解
1 事件三个阶段 捕获、目标、处理 (具体百度,后面有空补全)2import React from "react";class Test extends React.Component {parentRef;childRef;constructor(props) {super(props);this.parentRef React.createRef();this.chil…...

202302|读书笔记——国图点滴
杂志剪影|看一本赚一本系列 anywhere 随心而行随心而动,极简相生复古文艺 热情洋溢 色彩斑斓 极致优雅 深邃魅力 新生绽放 灿若星空 异彩纷呈含苞待放 惊艳绽放 爱在云端 空中婚礼 暗夜浪漫 策马逐梦橘影相映 浆果红唇 梦幻无暇 永无止境浮光掠影 微酥清风低调奢华…...

Linux 操作系统原理 — NUMA 架构中的多线程调度开销与性能优化
目录 文章目录 目录前言NUMA 架构中的多线程性能开销1、跨 Node 的 Memory 访问开销2、跨 Core 的多线程 Cache 同步开销3、多线程上下文切换开销4、多线程模式切换开销5、中断处理的开销6、TLB 缓存失效的开销7、内存拷贝的开销NUMA 架构中的性能优化:使用多核编程代替多线程…...
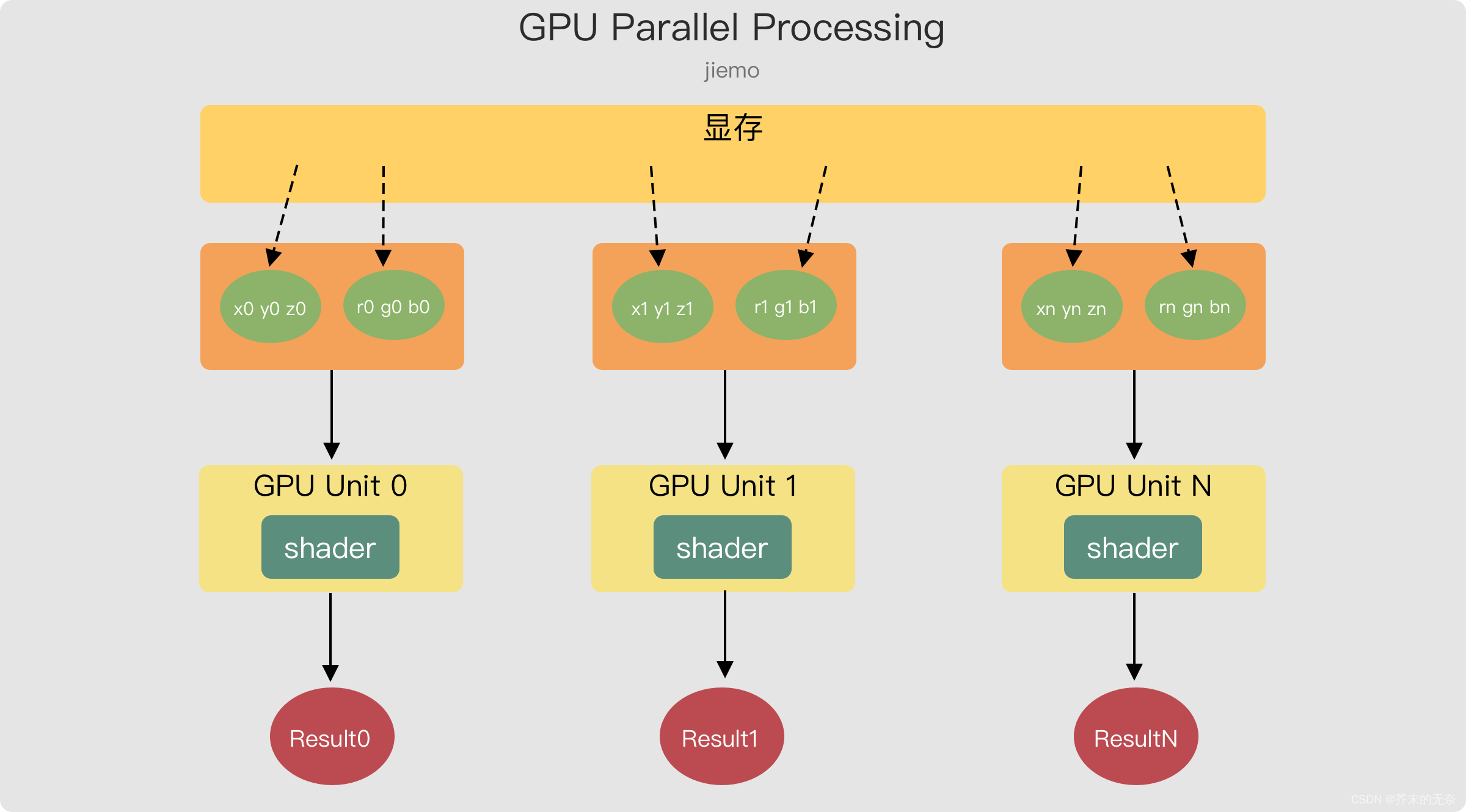
OpenGL - 如何理解 VAO 与 VBO 之间的关系
系列文章目录 LearnOpenGL 笔记 - 入门 01 OpenGLLearnOpenGL 笔记 - 入门 02 创建窗口LearnOpenGL 笔记 - 入门 03 你好,窗口LearnOpenGL 笔记 - 入门 04 你好,三角形 文章目录系列文章目录1. 前言2. 渲染管线的入口 - 顶点着色器2.1 顶点着色器处理过…...

Linux中sed的使用
语法: sed [选项] [sed内置命令字符] [输入文件]选项: 参数说明-n取消默认色的输出常与sed内置命令p一起使用-i直接将修改结果写入文件,不用-i,sed修改的是内存数据-e多次编译,不需要管道符了-r支持正则扩展 sed的内…...
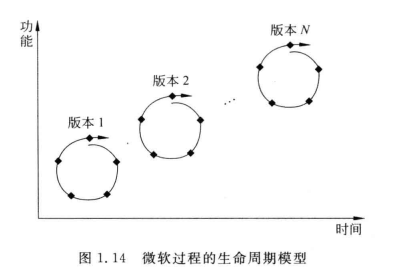
[软件工程导论(第六版)]第1章 软件工程学概述(复习笔记)
文章目录1.1 软件危机1.1.1 软件危机的介绍1.1.2 产生软件危机的原因1.1.3 消除软件危机的途径1.2 软件工程1.2.1 软件工程的介绍1.2.2 软件工程的基本原理1.2.3 软件工程方法学1.3 软件生命周期组成1.4 软件过程概念1.4.1 瀑布模型1.4.2 快速原型模型1.4.3 增量模型1.4.4 螺旋…...

ISP相关
Internet Service Provider,网络提供商/运营商,如电信、联通、移动等。 1. 与ISP互联的出口带宽 IDC或云提供商会与各运营商互联,互联的具体带宽数值一旦泄露,就会被恶意的攻击者利用。例如,若DDos攻击者知道了被攻击…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...
