【力扣刷题 | 第二十五天】

目录
前言:
474. 一和零 - 力扣(LeetCode)
总结:
前言:
今天我们依旧暴打动态规划
474. 一和零 - 力扣(LeetCode)
给你一个二进制字符串数组 strs 和两个整数 m 和 n 。
请你找出并返回 strs 的最大子集的长度,该子集中 最多 有 m 个 0 和 n 个 1 。
如果 x 的所有元素也是 y 的元素,集合 x 是集合 y 的 子集 。

其实这也是一个背包问题,只不过以前我们的限制条件只有一个重量,现在变成了两个,一个是,m,一个是n。那么我们就可以抽象的看他为一个二维的01背包问题。
那么我们就按照动态规划五部曲走:
1.确定dp数组的含义及其下标方式:dp[i][j] 表示装满 i 个0 和 j 个1 的背包中的最大子集长度
class Solution {
public:int findMaxForm(vector<string>& strs, int m, int n) {vector<vector<int>> dp(m + 1, vector<int> (n + 1, 0)); for (string str : strs) { int one = 0, zero = 0;for (char c : str) {if (c == '0') zero++;else one++;}for (int i = m; i >= zero; i--){ for (int j = n; j >= one; j--) {dp[i][j] = max(dp[i][j], dp[i - zero][j - one] + 1);}}}return dp[m][n];}};总结:
动态规划很难一眼看出来就是背包问题,要仔细甄别
如果我的内容对你有帮助,请点赞,评论,收藏。创作不易,大家的支持就是我坚持下去的动力!

相关文章:

【力扣刷题 | 第二十五天】
目录 前言: 474. 一和零 - 力扣(LeetCode) 总结: 前言: 今天我们依旧暴打动态规划 474. 一和零 - 力扣(LeetCode) 给你一个二进制字符串数组 strs 和两个整数 m 和 n 。 请你找出并返回 strs 的最大子集…...
GO学习之 函数(Function)
GO系列 1、GO学习之Hello World 2、GO学习之入门语法 3、GO学习之切片操作 4、GO学习之 Map 操作 5、GO学习之 结构体 操作 6、GO学习之 通道(Channel) 7、GO学习之 多线程(goroutine) 8、GO学习之 函数(Function) 9、GO学习之 接口(Interface) 文章目录 GO系列前言一、什么是…...

Jstack线上问题排查
1.top查找出哪个进程消耗的cpu高。执行top命令,默认是进程视图,其中PID是进程号(记下进程号) 2.top中shifth 或“H”查找出哪个线程消耗的cpu高 (记下最高的几个线程号) jstack 进程号 >> pid-cpu.…...
VIM 编辑器: Bram Moolenaar
VIM 用了很长时间, 个人的 VIM 配置文件差不多10年没有更新了。以前写程序的时候, 编辑都用这个。 linux kernel, boost规模的代码都不在话下。现在虽然代码写的少了,依然是我打开文件的首选。 现在用手机了,配个蓝牙键…...

鸿蒙应用开发指南:从零开始构建一款智能音乐播放器
介绍 随着鸿蒙操作系统的发布,开发者们迫不及待地想要探索鸿蒙应用的开发。本篇博客将以构建一款智能音乐播放器为例,带你一步步了解鸿蒙应用开发的技术要点和实践。我们将使用HarmonyOS的开发环境和MarkDown进行排版,方便你快速上手。 准备…...
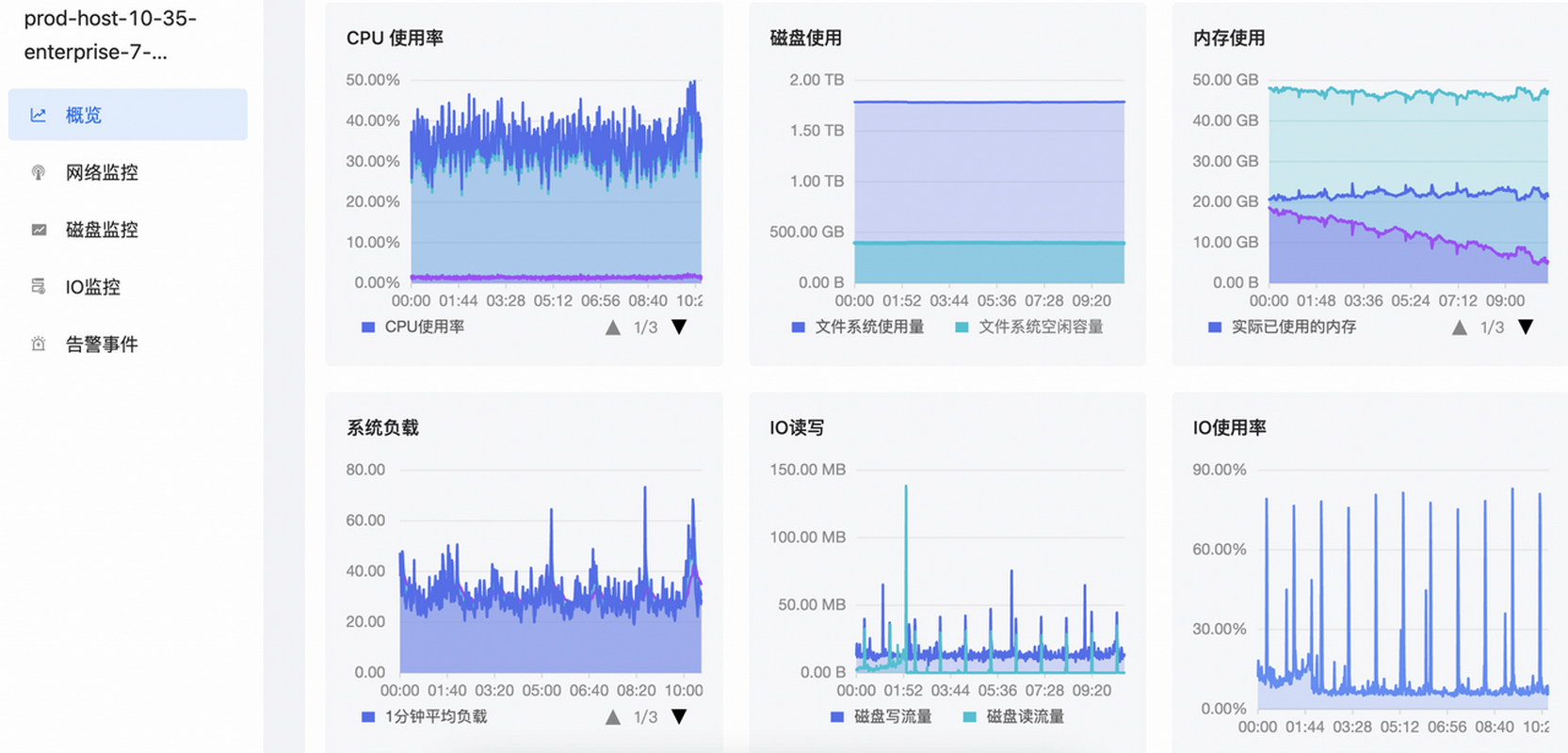
如何实现对主机的立体监控?
主机监控是保证系统稳定性和性能的重要环节之一,那应该如何实现对主机的立体监控? 本期EasyOps产品使用最佳实践,我们将为您揭晓: 主机应该如何分组和管理? 主机监控应该关注哪些关键性指标? 背 景 通…...
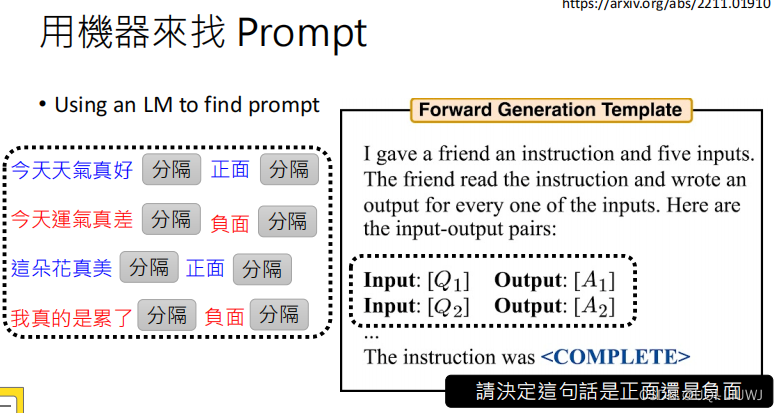
机器学习笔记:李宏毅ChatGPT Finetune VS Prompt
1 两种大语言模型:GPT VS BERT 2 对于大语言模型的两种不同期待 2.1 “专才” 2.1.1 成为专才的好处 Is ChatGPT A Good Translator? A Preliminary Study 2023 Arxiv 箭头方向指的是从哪个方向往哪个方向翻译 表格里面的数值越大表示翻译的越好 可以发现专门做翻…...
)
中电金信:逐数兴业 智启未来——“数据二十条”影响之解读 (下)
在逐数兴业 智启未来——“数据二十条”影响之解读(上)篇内容中,主要解读了有关于“数据二十条”发布的背景与意义、建立数据要素市场面临的挑战与应对。在今天的文章里,将继续解读“数据二十条”的主要内容以及对金融行业和金融科…...

54款宝藏级AIGC工具分享(claude,Midjourney,Stable Diffusion等)
随着ChatGPT的一波又一波高潮,生成式AI逐渐进入人们视野,并开始大行其道,正如人们所说:AI用的好,天天下班早! 当然,有效的利用AI不但能下班早,还能在上班时间摸鱼,就如潘…...
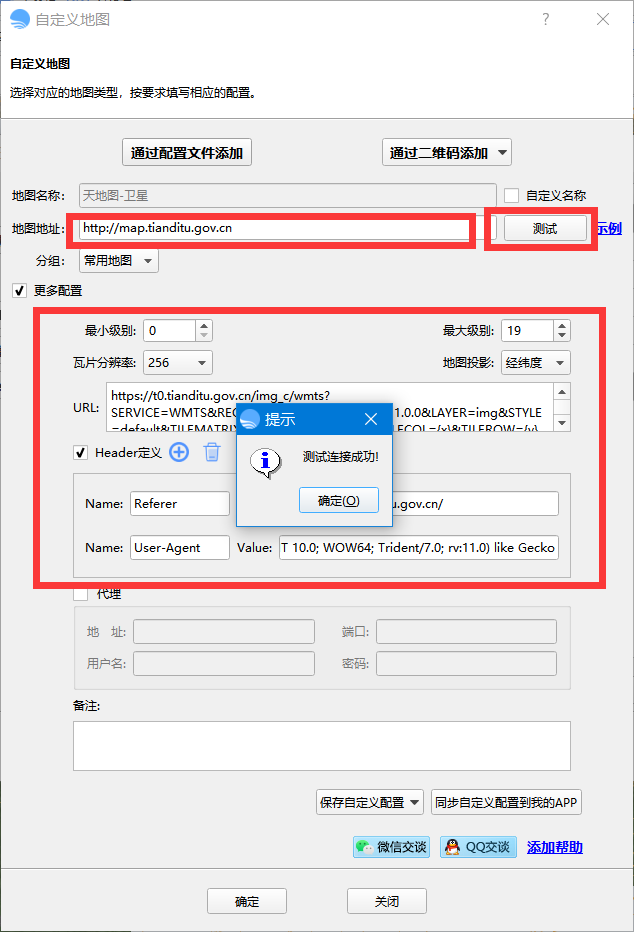
bigemap如何添加在线地图源?
第一步 打开浏览器,找到你要访问的地图的URL地址,并且确认可以正常在浏览器中访问;浏览器中不能访问,同样也不能在软件中访问。 以下为常用地图源地址: 天地图: http://map.tianditu.gov.cn 包含&a…...
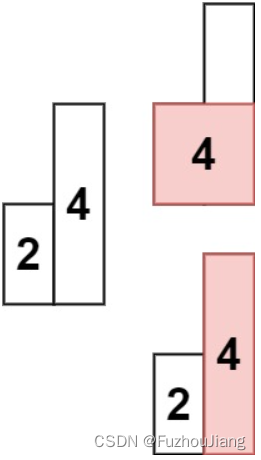
84. 柱状图中最大的矩形
题目描述 给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。 求在该柱状图中,能够勾勒出来的矩形的最大面积。 示例 1: 输入:heights [2,1,5,6,2,3] 输出:10 解释:最…...

嘉楠勘智k230开发板上手记录(二)--hello world
上次成功在k230上烧录sdk,这次准备实现hello world和ssh scp远程k230 主要是按照K230 SDK 基础教程的K230_实战基础篇_hello_world.md 一、PC连接k230 1. 初步准备 首先下载串口工具PuTTY,这个我个人感觉比较方便。 准备两根USB type-C数据线&#…...
ArcGIS Pro实践技术应用——暨基础入门、制图、空间分析、影像分析、三维建模、空间统计分析与建模、python融合、案例应用全流程科研能力提升
查看原文>>>ArcGIS Pro实践技术应用——暨基础入门、制图、空间分析、影像分析、三维建模、空间统计分析与建模、python融合能力 本文将利用ArcGIS Pro 将您的 GIS 工作组织到工程中,您可以使用 ArcGIS Pro 映射 2D 和 3D 数据。借助 ArcGIS Proÿ…...

学习pytorch
学习pytorch 1. 环境安装配置镜像源conda命令记录图像相关代码遇到的问题1. torch.cuda.is_available() False 1. 环境安装 B站小土堆视频 配置镜像源 conda config --show channels conda config --add channels https://mirrors.tuna.tsinghua.edu.cn/anaconda/pkgs/main…...

动态SQL实现原理一-动态SQL的使用
在介绍MyBatis动态SQL实现原理之前,我们先来了解一下MyBatis动态SQL的使用。顾名思义,动态SQL指的是事先无法预知具体的条件,需要在运行时根据具体的情况动态地生成SQL语句。 假设我们有一个获取用户信息查询操作,具体的查询条件…...
MyBatis动态sql标签帮你轻松搞定sql拼接
动态sql介绍 由于在开发过程不同的业务中会用到不同的操作条件,如果每个业务都拼接不同sql语句的话会是一个庞大的工作量;此时动态sql就能解决这个问题,可以针对不确定的操作条件动态拼接sql语句,根据提交的条件来完成业务sql的执…...
Java课题笔记~ 使用 Spring 的事务注解管理事务(掌握)
通过Transactional 注解方式,可将事务织入到相应 public 方法中,实现事务管理。 Transactional 的所有可选属性如下所示: propagation:用于设置事务传播属性。该属性类型为 Propagation 枚举, 默认值为 Propagation.R…...

UML—浅谈常用九种图
目录 概述: 1.用例图 2.静态图 3.行为图: 4.交互图: 5.实现图: 概述: UML的视图是由九种视图组成的,分别是用例图、类图、对象图、状态图、活动图、序列图、协作图、构件图、实施图。我们可以根据这9种图的功能和实现的目的…...
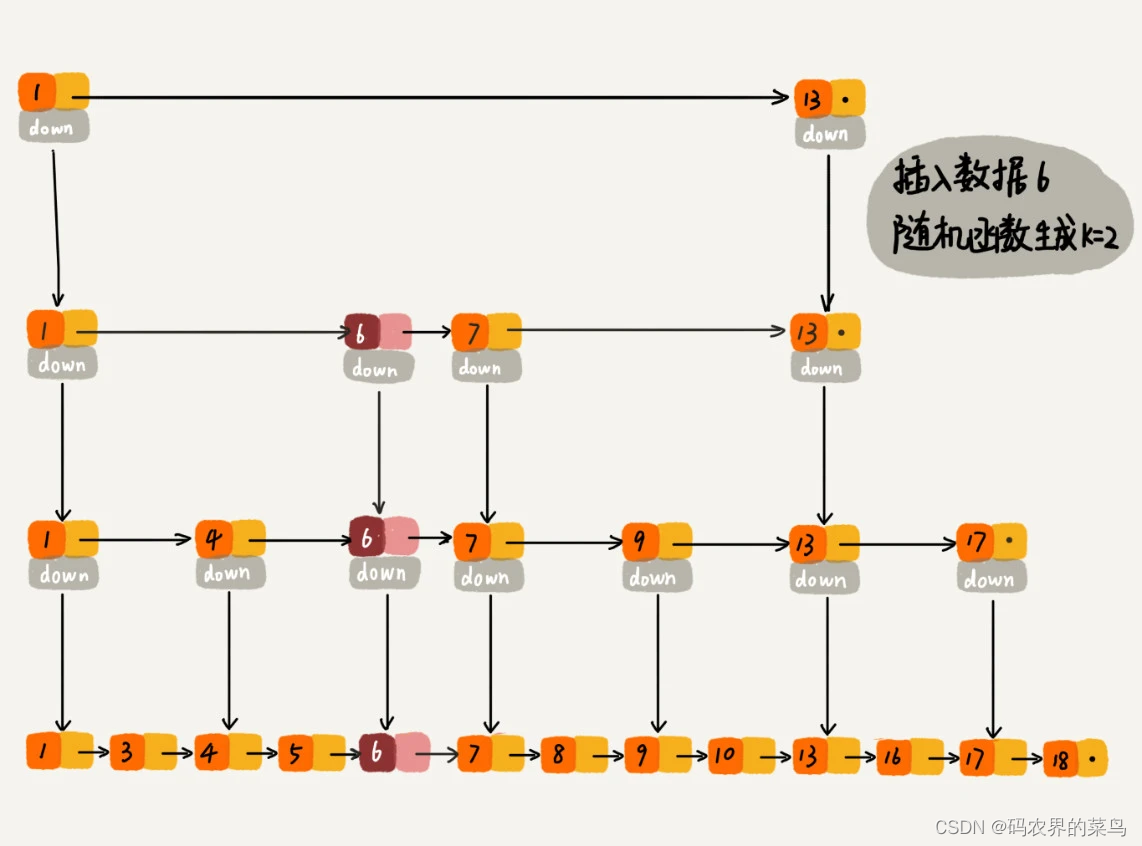
算法与数据结构-跳表
文章目录 什么是跳表跳表的时间复杂度跳表的空间复杂度如何高效的插入和删除跳表索引动态更新代码示例 什么是跳表 对于一个单链表来讲,即便链表中存储的数据是有序的,如果我们要想在其中查找某个数据,也只能从头到尾遍历链表。这样查找效率…...

微信小程序nodejs+vue+uniapp校运会高校运动会报名管理系统
3.1小程序端 小程序登录页面,用户也可以在此页面进行注册并且登录等。 登录成功后可以在我的个人中心查看自己的个人信息或者修改信息等 在广播信息中我们可以查看校运会发布的一些信息情况。 在首页我们可以看到校运会具体有什么项目运动。 在查看具体有什么活动我…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...
