Codeforces の 动态规划
Codeforces Round 785 (Div. 2) - C. Palindrome Basis
dp(9/100)
题目链接
思路:整数划分基础上加一个判断回文的条件
整数划分思路:背包容量为n,物品有体积为1~n n种,每种无数个,求使背包恰好装满的方案数——完全背包问题(传统的背包问题可能不会恰好装满,但此问题中如果背包有空余可以用1补齐,所以是一定会装满的)
#include <bits/stdc++.h>
// #pragma GCC optimize(3,"Ofast","inline")
// #pragma GCC optimize(2)
using namespace std;
typedef long long LL;
#define int LL
const int mod = 1e9 + 7;
const int N = 4e4 + 5;
int f[N];void solve()
{ int n;cin >> n;cout << f[n] << endl;
}signed main()
{ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);int t = 1;cin >> t;f[0] = 1;for (int i = 1; i <= 4e4; i ++ ){string a = to_string(i);string b = a;reverse(a.begin(), a.end());if(a == b)for (int j = i; j <= 4e4; j ++ )f[j] = (f[j] + f[j - i]) % mod; }while(t -- ) solve(); system("pause");return 0;
}
Codeforces Round 113 (Div. 2) - E. Tetrahedron
dp(18/100)
题目链接
走n步的路线数是走n-2步的三倍加上走n-1步的两倍
当走到n-2步到达D点时,还可向A B C三个方向走一来一回
例如:
f[0] = 1(没有走动,就在原点)路线:D
f[2] 路线就有:
D - A - D;
D - B - D
D - C - D
走到n-1步到达D点的情况,可在当前步向除D以外的另外两点走一步再回到D。
例如:
f[3] 路线有:
D - A - B - D
D - A - C - D
D - B - A - D
D - B - C -D
D - C - A - D
D - C- B - D
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 1e7 + 10, mod = 1e9 + 7;
int f[N];void solve()
{int n;cin >> n;f[0] = 1;f[1] = 0;for (int i = 2; i <= n; i ++ )f[i] = (2 * f[i - 1] + 3 * f[i - 2]) % mod;cout << f[n] << endl;
}signed main()
{int t = 1;// cin >> t;while(t -- ) solve();return 0;
}
相关文章:

Codeforces の 动态规划
Codeforces Round 785 (Div. 2) - C. Palindrome Basis dp(9/100) 题目链接 思路:整数划分基础上加一个判断回文的条件 整数划分思路:背包容量为n,物品有体积为1~n n种,每种无数个,求使背包恰好装满的方案数——完全背…...
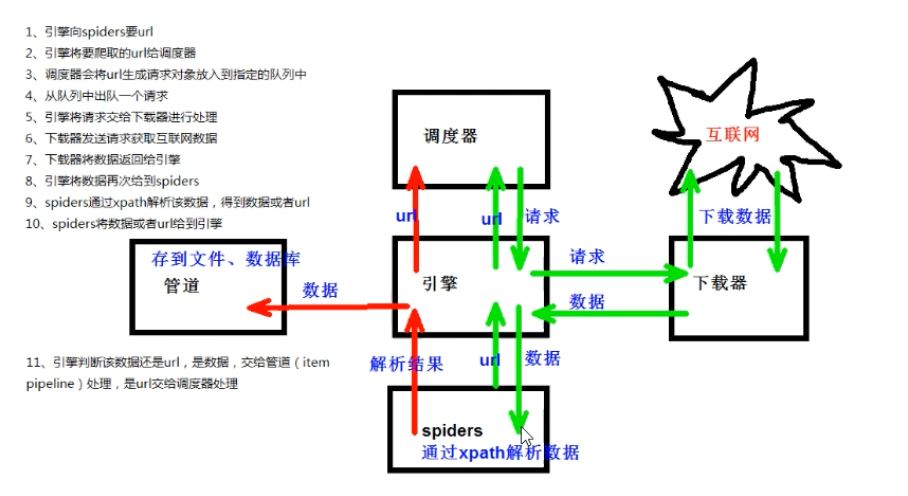
数学建模-爬虫系统学习
尚硅谷Python爬虫教程小白零基础速通(含python基础爬虫案例) 内容包括:Python基础、Urllib、解析(xpath、jsonpath、beautiful)、requests、selenium、Scrapy框架 python基础 进阶(字符串 列表 元组 字典…...
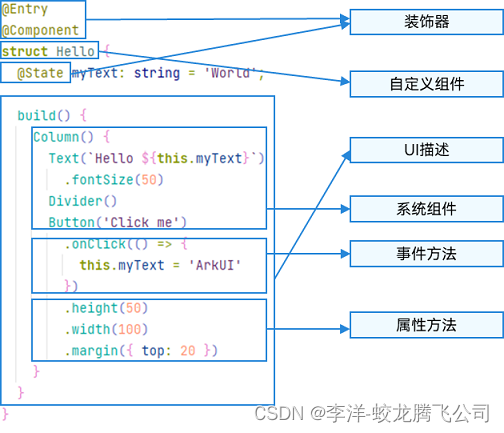
HarmonyOS/OpenHarmony应用开发-ArkTS语言渲染控制概述
ArkUI通过自定义组件的build()函数和builder装饰器中的声明式UI描述语句构建相应的UI。 在声明式描述语句中开发者除了使用系统组件外,还可以使用渲染控制语句来辅助UI的构建,这些渲染控制语句包括控制组件是否显示的条件渲染语句,基于数组数…...

【力扣刷题 | 第二十五天】
目录 前言: 474. 一和零 - 力扣(LeetCode) 总结: 前言: 今天我们依旧暴打动态规划 474. 一和零 - 力扣(LeetCode) 给你一个二进制字符串数组 strs 和两个整数 m 和 n 。 请你找出并返回 strs 的最大子集…...
GO学习之 函数(Function)
GO系列 1、GO学习之Hello World 2、GO学习之入门语法 3、GO学习之切片操作 4、GO学习之 Map 操作 5、GO学习之 结构体 操作 6、GO学习之 通道(Channel) 7、GO学习之 多线程(goroutine) 8、GO学习之 函数(Function) 9、GO学习之 接口(Interface) 文章目录 GO系列前言一、什么是…...

Jstack线上问题排查
1.top查找出哪个进程消耗的cpu高。执行top命令,默认是进程视图,其中PID是进程号(记下进程号) 2.top中shifth 或“H”查找出哪个线程消耗的cpu高 (记下最高的几个线程号) jstack 进程号 >> pid-cpu.…...
VIM 编辑器: Bram Moolenaar
VIM 用了很长时间, 个人的 VIM 配置文件差不多10年没有更新了。以前写程序的时候, 编辑都用这个。 linux kernel, boost规模的代码都不在话下。现在虽然代码写的少了,依然是我打开文件的首选。 现在用手机了,配个蓝牙键…...

鸿蒙应用开发指南:从零开始构建一款智能音乐播放器
介绍 随着鸿蒙操作系统的发布,开发者们迫不及待地想要探索鸿蒙应用的开发。本篇博客将以构建一款智能音乐播放器为例,带你一步步了解鸿蒙应用开发的技术要点和实践。我们将使用HarmonyOS的开发环境和MarkDown进行排版,方便你快速上手。 准备…...
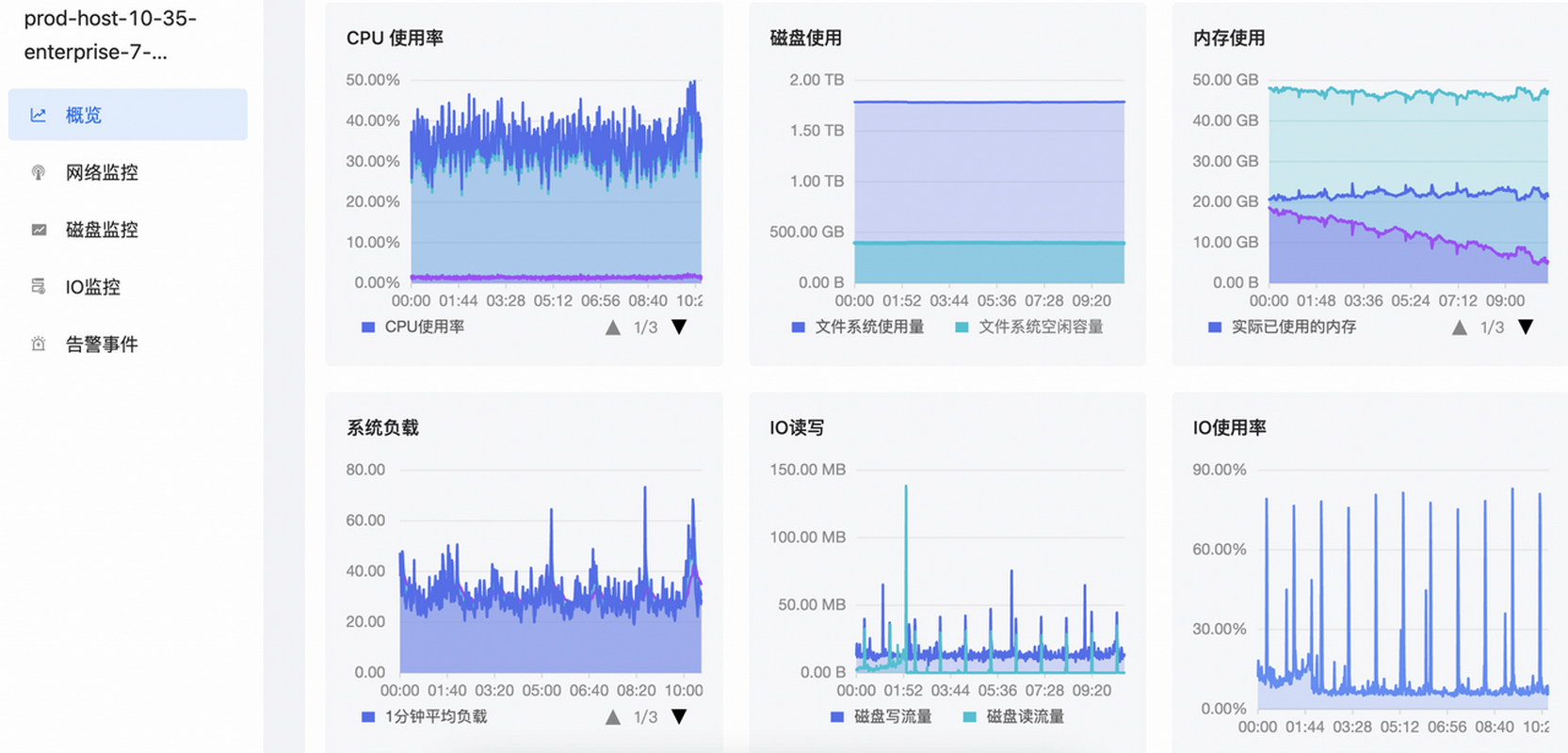
如何实现对主机的立体监控?
主机监控是保证系统稳定性和性能的重要环节之一,那应该如何实现对主机的立体监控? 本期EasyOps产品使用最佳实践,我们将为您揭晓: 主机应该如何分组和管理? 主机监控应该关注哪些关键性指标? 背 景 通…...
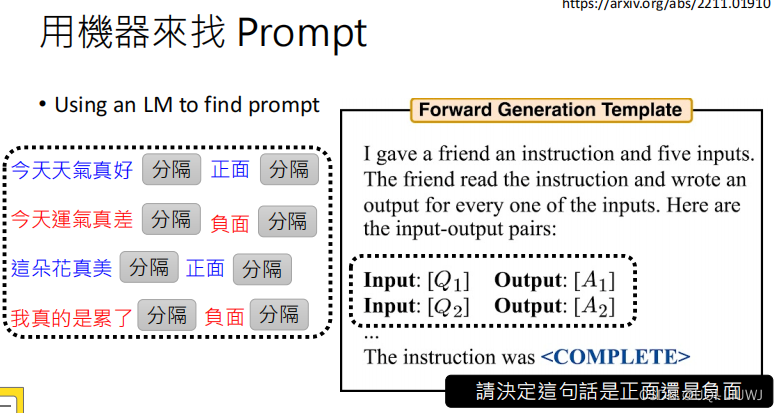
机器学习笔记:李宏毅ChatGPT Finetune VS Prompt
1 两种大语言模型:GPT VS BERT 2 对于大语言模型的两种不同期待 2.1 “专才” 2.1.1 成为专才的好处 Is ChatGPT A Good Translator? A Preliminary Study 2023 Arxiv 箭头方向指的是从哪个方向往哪个方向翻译 表格里面的数值越大表示翻译的越好 可以发现专门做翻…...
)
中电金信:逐数兴业 智启未来——“数据二十条”影响之解读 (下)
在逐数兴业 智启未来——“数据二十条”影响之解读(上)篇内容中,主要解读了有关于“数据二十条”发布的背景与意义、建立数据要素市场面临的挑战与应对。在今天的文章里,将继续解读“数据二十条”的主要内容以及对金融行业和金融科…...

54款宝藏级AIGC工具分享(claude,Midjourney,Stable Diffusion等)
随着ChatGPT的一波又一波高潮,生成式AI逐渐进入人们视野,并开始大行其道,正如人们所说:AI用的好,天天下班早! 当然,有效的利用AI不但能下班早,还能在上班时间摸鱼,就如潘…...
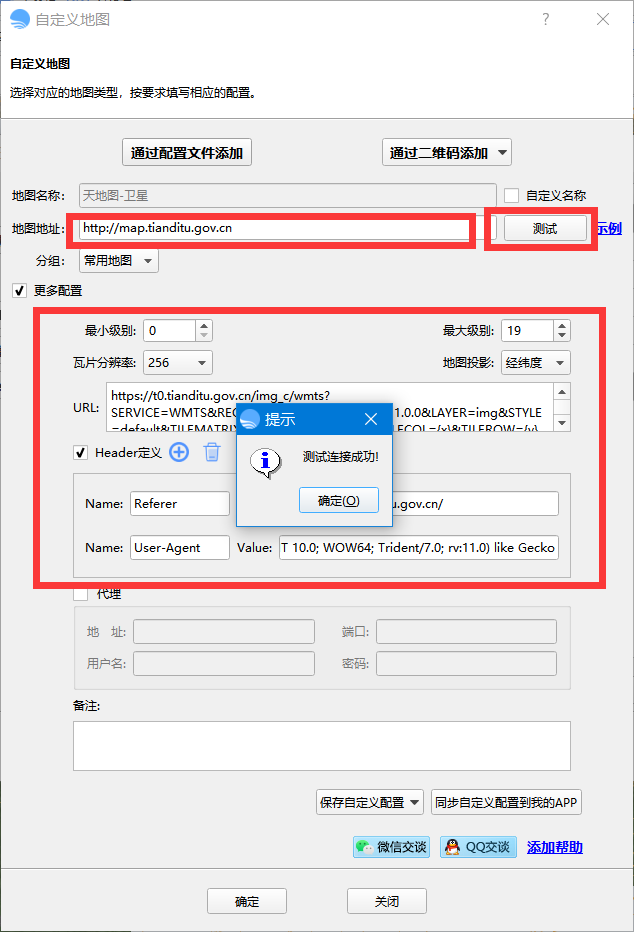
bigemap如何添加在线地图源?
第一步 打开浏览器,找到你要访问的地图的URL地址,并且确认可以正常在浏览器中访问;浏览器中不能访问,同样也不能在软件中访问。 以下为常用地图源地址: 天地图: http://map.tianditu.gov.cn 包含&a…...
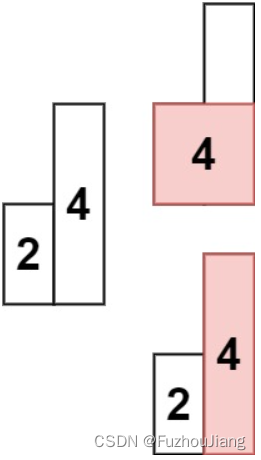
84. 柱状图中最大的矩形
题目描述 给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。 求在该柱状图中,能够勾勒出来的矩形的最大面积。 示例 1: 输入:heights [2,1,5,6,2,3] 输出:10 解释:最…...

嘉楠勘智k230开发板上手记录(二)--hello world
上次成功在k230上烧录sdk,这次准备实现hello world和ssh scp远程k230 主要是按照K230 SDK 基础教程的K230_实战基础篇_hello_world.md 一、PC连接k230 1. 初步准备 首先下载串口工具PuTTY,这个我个人感觉比较方便。 准备两根USB type-C数据线&#…...
ArcGIS Pro实践技术应用——暨基础入门、制图、空间分析、影像分析、三维建模、空间统计分析与建模、python融合、案例应用全流程科研能力提升
查看原文>>>ArcGIS Pro实践技术应用——暨基础入门、制图、空间分析、影像分析、三维建模、空间统计分析与建模、python融合能力 本文将利用ArcGIS Pro 将您的 GIS 工作组织到工程中,您可以使用 ArcGIS Pro 映射 2D 和 3D 数据。借助 ArcGIS Proÿ…...

学习pytorch
学习pytorch 1. 环境安装配置镜像源conda命令记录图像相关代码遇到的问题1. torch.cuda.is_available() False 1. 环境安装 B站小土堆视频 配置镜像源 conda config --show channels conda config --add channels https://mirrors.tuna.tsinghua.edu.cn/anaconda/pkgs/main…...

动态SQL实现原理一-动态SQL的使用
在介绍MyBatis动态SQL实现原理之前,我们先来了解一下MyBatis动态SQL的使用。顾名思义,动态SQL指的是事先无法预知具体的条件,需要在运行时根据具体的情况动态地生成SQL语句。 假设我们有一个获取用户信息查询操作,具体的查询条件…...
MyBatis动态sql标签帮你轻松搞定sql拼接
动态sql介绍 由于在开发过程不同的业务中会用到不同的操作条件,如果每个业务都拼接不同sql语句的话会是一个庞大的工作量;此时动态sql就能解决这个问题,可以针对不确定的操作条件动态拼接sql语句,根据提交的条件来完成业务sql的执…...
Java课题笔记~ 使用 Spring 的事务注解管理事务(掌握)
通过Transactional 注解方式,可将事务织入到相应 public 方法中,实现事务管理。 Transactional 的所有可选属性如下所示: propagation:用于设置事务传播属性。该属性类型为 Propagation 枚举, 默认值为 Propagation.R…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...
零知开源——STM32F103RBT6驱动 ICM20948 九轴传感器及 vofa + 上位机可视化教程
STM32F1 本教程使用零知标准板(STM32F103RBT6)通过I2C驱动ICM20948九轴传感器,实现姿态解算,并通过串口将数据实时发送至VOFA上位机进行3D可视化。代码基于开源库修改优化,适合嵌入式及物联网开发者。在基础驱动上新增…...

深度学习之模型压缩三驾马车:模型剪枝、模型量化、知识蒸馏
一、引言 在深度学习中,我们训练出的神经网络往往非常庞大(比如像 ResNet、YOLOv8、Vision Transformer),虽然精度很高,但“太重”了,运行起来很慢,占用内存大,不适合部署到手机、摄…...

pycharm 设置环境出错
pycharm 设置环境出错 pycharm 新建项目,设置虚拟环境,出错 pycharm 出错 Cannot open Local Failed to start [powershell.exe, -NoExit, -ExecutionPolicy, Bypass, -File, C:\Program Files\JetBrains\PyCharm 2024.1.3\plugins\terminal\shell-int…...

【无标题】湖北理元理律师事务所:债务优化中的生活保障与法律平衡之道
文/法律实务观察组 在债务重组领域,专业机构的核心价值不仅在于减轻债务数字,更在于帮助债务人在履行义务的同时维持基本生活尊严。湖北理元理律师事务所的服务实践表明,合法债务优化需同步实现三重平衡: 法律刚性(债…...

java高级——高阶函数、如何定义一个函数式接口类似stream流的filter
java高级——高阶函数、stream流 前情提要文章介绍一、函数伊始1.1 合格的函数1.2 有形的函数2. 函数对象2.1 函数对象——行为参数化2.2 函数对象——延迟执行 二、 函数编程语法1. 函数对象表现形式1.1 Lambda表达式1.2 方法引用(Math::max) 2 函数接口…...
