【1237. 找出给定方程的正整数解】
来源:力扣(LeetCode)
描述:
给你一个函数 f(x, y) 和一个目标结果 z,函数公式未知,请你计算方程 f(x,y) == z 所有可能的正整数 数对 x 和 y。满足条件的结果数对可以按任意顺序返回。
尽管函数的具体式子未知,但它是单调递增函数,也就是说:
- f(x, y) < f(x + 1, y)
- f(x, y) < f(x, y + 1)
函数接口定义如下:
interface CustomFunction {
public:// Returns some positive integer f(x, y) for two positive integers x and y based on a formula.int f(int x, int y);
};
你的解决方案将按如下规则进行评判:
- 判题程序有一个由
CustomFunction的9种实现组成的列表,以及一种为特定的z生成所有有效数对的答案的方法。 - 判题程序接受两个输入:
function_id(决定使用哪种实现测试你的代码)以及目标结果 z 。 - 判题程序将会调用你实现的
findSolution并将你的结果与答案进行比较。 - 如果你的结果与答案相符,那么解决方案将被视作正确答案,即
Accepted。
示例 1:
输入:function_id = 1, z = 5
输出:[[1,4],[2,3],[3,2],[4,1]]
解释:function_id = 1 暗含的函数式子为 f(x, y) = x + y
以下 x 和 y 满足 f(x, y) 等于 5:
x=1, y=4 -> f(1, 4) = 1 + 4 = 5
x=2, y=3 -> f(2, 3) = 2 + 3 = 5
x=3, y=2 -> f(3, 2) = 3 + 2 = 5
x=4, y=1 -> f(4, 1) = 4 + 1 = 5
示例 2:
输入:function_id = 2, z = 5
输出:[[1,5],[5,1]]
解释:function_id = 2 暗含的函数式子为 f(x, y) = x * y
以下 x 和 y 满足 f(x, y) 等于 5:
x=1, y=5 -> f(1, 5) = 1 * 5 = 5
x=5, y=1 -> f(5, 1) = 5 * 1 = 5
提示:
- 1 <= function_id <= 9
- 1 <= z <= 100
- 题目保证 f(x, y) == z 的解处于 1 <= x, y <= 1000 的范围内。
- 在 1 <= x, y <= 1000 的前提下,题目保证 f(x, y) 是一个 32 位有符号整数。
方法一:枚举
根据题目给出的 x 和 y 的取值范围,枚举所有的 x, y 数对,保存满足 f(x, y) = z 的数对,最后返回结果。
代码:
class Solution {
public:vector<vector<int>> findSolution(CustomFunction& customfunction, int z) {vector<vector<int>> res;for (int x = 1; x <= 1000; x++) {for (int y = 1; y <= 1000; y++) {if (customfunction.f(x, y) == z) {res.push_back({x, y});}}}return res;}
};
执行用时:124 ms, 在所有 C++ 提交中击败了13.98%的用户
内存消耗:6.2 MB, 在所有 C++ 提交中击败了80.64%的用户
复杂度分析
时间复杂度:O(mn),其中 m 是 x 的取值数目,n 是 y 的取值数目。
空间复杂度:O(1)。返回值不计入空间复杂度。
方法二:二分查找
我们固定 x = x0 时,函数 g(y) = f(x0, y) 是单调递增函数,可以通过二分查找来判断是否存在 y = y0 ,使 g(y0) = f(x0, y0) = z 成立。
代码:
class Solution {
public:vector<vector<int>> findSolution(CustomFunction& customfunction, int z) {vector<vector<int>> res;for (int x = 1; x <= 1000; x++) {int yleft = 1, yright = 1000;while (yleft <= yright) {int ymiddle = (yleft + yright) / 2;if (customfunction.f(x, ymiddle) == z) {res.push_back({x, ymiddle});break;}if (customfunction.f(x, ymiddle) > z) {yright = ymiddle - 1;} else {yleft = ymiddle + 1;}}}return res;}
};
执行用时:4 ms, 在所有 C++ 提交中击败了51.61%的用户
内存消耗:6.1 MB, 在所有 C++ 提交中击败了96.77%的用户
复杂度分析
时间复杂度:O(mlogn),其中 m 是 x 的取值数目,n 是 y 的取值数目。
空间复杂度:O(1)。返回值不计入空间复杂度。
方法三:双指针
假设 x1 < x2,且 f(x1, y1) = f(x2, y2) = z,显然有 y1 > y2。因此我们从小到大进行枚举 x,并且从大到小枚举 y,当固定 x 时,不需要重头开始枚举所有的 y,只需要从上次结束的值开始枚举即可。
代码:
class Solution {
public:vector<vector<int>> findSolution(CustomFunction& customfunction, int z) {vector<vector<int>> res;for (int x = 1, y = 1000; x <= 1000 && y >= 1; x++) {while (y >= 1 && customfunction.f(x, y) > z) {y--;}if (y >= 1 && customfunction.f(x, y) == z) {res.push_back({x, y});}}return res;}
};
执行用时:4 ms, 在所有 C++ 提交中击败了51.61%的用户
内存消耗:6.3 MB, 在所有 C++ 提交中击败了17.20%的用户
复杂度分析
时间复杂度:O(m+n),其中 m 是 x 的取值数目,n 是 y 的取值数目。
空间复杂度:O(1)。返回值不计入空间复杂度。
author:LeetCode-Solution
相关文章:

【1237. 找出给定方程的正整数解】
来源:力扣(LeetCode) 描述: 给你一个函数 f(x, y) 和一个目标结果 z,函数公式未知,请你计算方程 f(x,y) z 所有可能的正整数 数对 x 和 y。满足条件的结果数对可以按任意顺序返回。 尽管函数的具体式子…...

java基础学习 day41(继承中成员变量和成员方法的访问特点,方法的重写)
继承中,成员变量的访问特点 a. name前什么都不加,name变量的访问采用就近原则,先在局部变量中查找,若没找到,继续在本类的成员变量中查找,若没找到,继续在直接父类的成员变量中查找,…...

【c语言进阶】深度剖析整形数据
🚀write in front🚀 📜所属专栏: 🛰️博客主页:睿睿的博客主页 🛰️代码仓库:🎉VS2022_C语言仓库 🎡您的点赞、关注、收藏、评论,是对我最大的激励…...
)
【信息系统项目管理师】项目管理十大知识领域记忆敲出(采购风险沟通干系人)
【信息系统项目管理师】项目管理十大知识领域记忆敲出(采购风险沟通干系人) 这里写目录标题【信息系统项目管理师】项目管理十大知识领域记忆敲出(采购风险沟通干系人)一.项目采购管理记忆敲出1.合同管理:2.规划采购管…...
[LeetCode 1237]找出给定方程的正整数解
题目描述 题目链接:[LeetCode 1237]找出给定方程的正整数解 给你一个函数 f(x, y) 和一个目标结果 z,函数公式未知,请你计算方程 f(x,y) z 所有可能的正整数 数对 x 和 y。满足条件的结果数对可以按任意顺序返回。 尽管函数的具体式子未知…...
6.2 构建 RESTful 应用接口
第6章 构建 RESTful 服务 6.1 RESTful 简介 6.2 构建 RESTful 应用接口 6.3 使用 Swagger 生成 Web API 文档 6.4 实战:实现 Web API 版本控制 6.2 构建 RESTful 应用接口 6.2.1 Spring Boot 对 RESTful 的支持 Spring Boot 提供的spring-boot-starter-web组件完全…...

20230218英语学习
How Italian Artist’s Mild Colors Dominate World of Design 温柔的“莫兰迪色”,如何引领设计时尚? The Morandi color scheme has become an across-the-board fashion that now prevails in the world of design.Soft and sophisticated Morandi c…...

Linux单一服务管理systemctl
基本上systemd这个启动服务机制只有systemctl命令来处理,所以全部的操作都需要使用systemctl systemctl管理单一服务 一般来说服务的启动有两个阶段,一个是开机是否启动,以及现在是否启动 systemctl【command】【unit】 command主要有&…...
【GStreamer 】 TX1中CPU和GPU解码显示海康相机RTSP流
大家好,我是虎哥,今天找了一套海康的相机,想后续测试一下DeepStream用网络相机RTSP流做输入看看后续目标识别和分类。但是还是想先实时看看视频,当然,可以选择VLC去查看,顺道我也用GStreamer 来测试了一下&…...

匿名内部类、Lambda表达式、方法引用对比分析
文章目录一、匿名内部类1. 语法格式2. 使用方法① 传统方式② 匿名内部类方式二、Lambda表达式1. 语法格式2. 使用方法① 匿名内部类方式② Lambda表达式方式三、方法引用1. 语法格式2. 使用方法① 类型的静态方法引用② 类型的构造方法引用③ 类型的实例方法引用④ 对象的实例…...
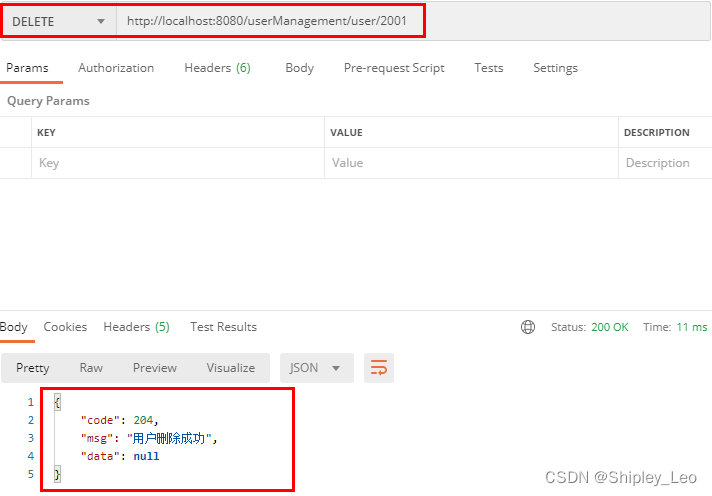
ESXi主机CVE-2021-21972漏洞复现安全处置建议
一、漏洞简介 vSphere 是 VMware 推出的虚拟化平台套件,包含 ESXi、vCenter Server 等一系列的软件。其中 vCenter Server 为 ESXi 的控制中心,可从单一控制点统一管理数据中心的所有 vSphere 主机和虚拟机。 vSphere Client(HTML5…...

研报精选230217
目录 【行业230217毕马威】奢侈品行业新气象【行业230217国信证券】医药生物行业2023年2月投资策略:持续关注疫后复苏和创新两大主线【行业230217国金证券】航空锻造:稳定格局筑专业化壁垒,顺势而为拓产业链深度【个股230217西南证券_招商轮船…...
(std::unordered_set)(一))
c++11 标准模板(STL)(std::unordered_set)(一)
定义于头文件 <unordered_set> template< class Key, class Hash std::hash<Key>, class KeyEqual std::equal_to<Key>, class Allocator std::allocator<Key> > class unordered_set;(1)(C11 起)namespace pmr { templ…...

【C语言进阶】你听说过柔性数组吗?
👦个人主页:Weraphael ✍🏻作者简介:目前是C语言学习者 ✈️专栏:C语言航路 🐋 希望大家多多支持,咱一起进步!😁 如果文章对你有帮助的话 欢迎 评论💬 点赞&a…...

[LeetCode]1237. 找出给定方程的正整数解
题目链接:https://leetcode.cn/problems/find-positive-integer-solution-for-a-given-equation/description/ 题目描述: 样例1: 输入:function_id 1, z 5 输出:[[1,4],[2,3],[3,2],[4,1]] 解释:functi…...

【路径规划】基于A*算法和Dijkstra算法的路径规划(Python代码实现)
👨🎓个人主页:研学社的博客💥💥💞💞欢迎来到本博客❤️❤️💥💥🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密…...

蓝桥杯 stm32 PWM 设置占空比
本文代码使用 HAL 库。 文章目录 前言一、创建CubeMX 工程 ,占空比分析:二、相关函数:1. 获取 CNT函数2.设置CNT为 0 函数(计算器清零)3.开启TIM2_CH1的输入捕获中断函数4.TIM 回调函数三、设置上升沿,下降沿四、在lcd上显示 R40 占空比 详细代码五、设置占空比,输出 PW…...
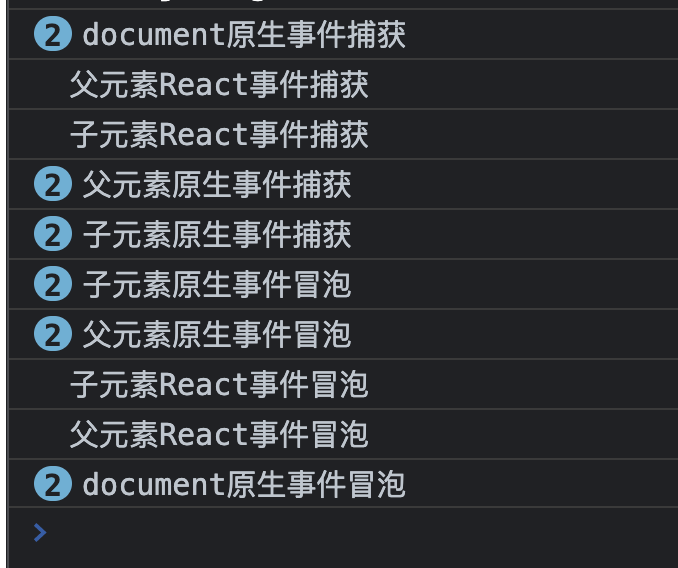
React 合成事件理解
1 事件三个阶段 捕获、目标、处理 (具体百度,后面有空补全)2import React from "react";class Test extends React.Component {parentRef;childRef;constructor(props) {super(props);this.parentRef React.createRef();this.chil…...

202302|读书笔记——国图点滴
杂志剪影|看一本赚一本系列 anywhere 随心而行随心而动,极简相生复古文艺 热情洋溢 色彩斑斓 极致优雅 深邃魅力 新生绽放 灿若星空 异彩纷呈含苞待放 惊艳绽放 爱在云端 空中婚礼 暗夜浪漫 策马逐梦橘影相映 浆果红唇 梦幻无暇 永无止境浮光掠影 微酥清风低调奢华…...

Linux 操作系统原理 — NUMA 架构中的多线程调度开销与性能优化
目录 文章目录 目录前言NUMA 架构中的多线程性能开销1、跨 Node 的 Memory 访问开销2、跨 Core 的多线程 Cache 同步开销3、多线程上下文切换开销4、多线程模式切换开销5、中断处理的开销6、TLB 缓存失效的开销7、内存拷贝的开销NUMA 架构中的性能优化:使用多核编程代替多线程…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...
