电子技术——CS和CE放大器的高频响应
电子技术——CS和CE放大器的高频响应

在绘制出MOS和BJT的高频响应模型之后,我们对MOS和BJT的高频响应有了进一步的认识。现在我们想知道的是在高频响应中 fHf_HfH 的关系。
高频响应分析对电容耦合还是直接耦合都是适用的,因为在电容耦合中高频模式下此时电容可以看做是完美短路。
CS放大器
下图是一个CS放大器的高频模型:
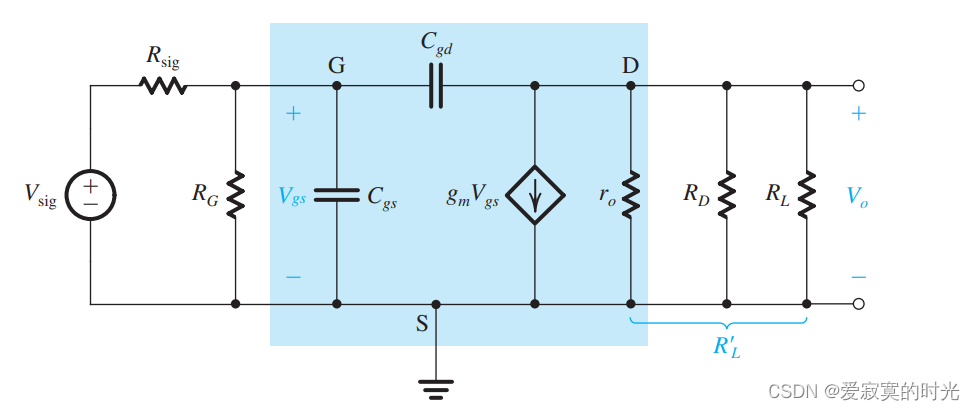
其中输入端和输出端可以使用戴维南等效定理替代:
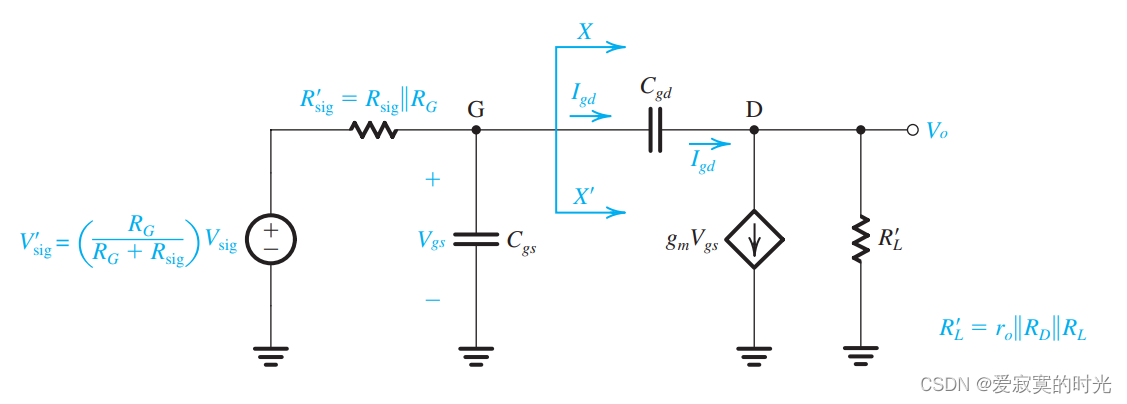
上图中,当 CgsC_{gs}Cgs 和 CgdC_{gd}Cgd 均为零的时候,此时获得最大增益 ∣AM∣|A_M|∣AM∣ :
AM=−RGRG+Rsig(gmRL′)A_M = -\frac{R_G}{R_G + R_{sig}}(g_m R_L') AM=−RG+RsigRG(gmRL′)
通过上述的等效电路,我们当然可以写出一个关于复频率 sss 的传递方程 Vo/VsigV_o / V_{sig}Vo/Vsig 。因为图中存在两个电容的,则传递方程一定是一个二阶多项式方程。之后便可以确定零点和极点。但是,这个方法还是比较困难的,而且无法给我们一个有效的方式快速确实什么才是高频响应的决定因素。为此我们需要一个更加绝妙的方法。所以我们不打算计算传递方程,而是使用估算的方法快速确定高频响应的决定因素。
我们的思路在输入端简化电路,然后使用简单的RC低通网络解决。所以,我们要去掉电容 CgdC_{gd}Cgd ,寻找一个等价的 CeqC_{eq}Ceq 代替。
首先我们考虑放大器的输出端,其电压为:
Vo=−(gmVgs)RL′+IgdRL′V_o = -(g_m V_{gs})R_L' + I_{gd}R_L' Vo=−(gmVgs)RL′+IgdRL′
因为 gmVgs≫Igdg_m V_{gs} \gg I_{gd}gmVgs≫Igd 所以:
Vo≃−(gmVgs)RL′V_o \simeq -(g_m V_{gs})R_L' Vo≃−(gmVgs)RL′
再观察电流 IgdI_{gd}Igd :
Igd=sCgd(Vgs−Vo)=sCgd[Vgs−(−gmRL′Vgs)]=sCgd(1+gmRL′)VgsI_{gd} = sC_{gd}(V_{gs} - V_o) = sC_{gd}[V_{gs} - (-g_mR_L'V_{gs})] = sC_{gd}(1 + g_mR_L')V_{gs} Igd=sCgd(Vgs−Vo)=sCgd[Vgs−(−gmRL′Vgs)]=sCgd(1+gmRL′)Vgs
现在,我们从 XX′XX'XX′ 方向向右看去,流过的电流是 IgdI_{gd}Igd 因此,我们只需要使用一个从栅极到地的等效电容 GeqG_{eq}Geq 并且使得其流过的电流仍然为 IgdI_{gd}Igd 即可。
sCeqVgs=sCgd(1+gmRL′)VgssC_{eq}V_{gs} = sC_{gd}(1 + g_mR_L')V_{gs} sCeqVgs=sCgd(1+gmRL′)Vgs
因此:
Ceq=Cgd(1+gmRL′)C_{eq} = C_{gd}(1 + g_mR_L') Ceq=Cgd(1+gmRL′)
现在 CgdC_{gd}Cgd 变成了较大的输入端电容 CeqC_{eq}Ceq 。如图:
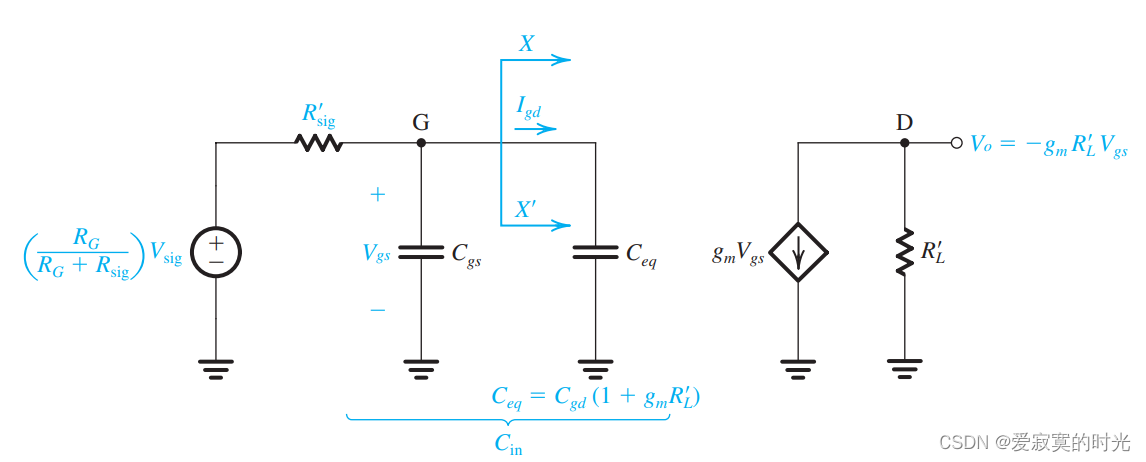
乘以因子 (1+gmRL′)(1 + g_mR_L')(1+gmRL′) 是因为 CgdC_{gd}Cgd 连接在G与D直接,并且之间存在一个电压增益 gmRL′g_mR_L'gmRL′ 。这个效应称为 米勒效应 。因子 (1+gmRL′)(1 + g_mR_L')(1+gmRL′) 称为 米勒因子 。
现在输入端变成了一个简单的RC低通型STC网络:
Vgs=(RGRG+RsigVsig)11+sω0V_{gs} = (\frac{R_G}{R_G + R_{sig}}V_{sig})\frac{1}{1 + \frac{s}{\omega_0}} Vgs=(RG+RsigRGVsig)1+ω0s1
这里 ω0\omega_0ω0 是极点频率:
ω0=1/CinRsig′\omega_0 = 1/C_{in}R_{sig}' ω0=1/CinRsig′
这里 CinC_{in}Cin 为:
Cin=Cgs+CeqC_{in} = C_{gs} + C_{eq} Cin=Cgs+Ceq
最后我们就可以得到:
VoVsig=−(RGRG+Rsig)(gmRL′)(11+sω0)\frac{V_o}{V_{sig}} = -(\frac{R_G}{R_G + R_{sig}})(g_m R_L')(\frac{1}{1 + \frac{s}{\omega_0}}) VsigVo=−(RG+RsigRG)(gmRL′)(1+ω0s1)
也就是:
VoVsig=AM1+sωH\frac{V_o}{V_{sig}} = \frac{A_M}{1 + \frac{s}{\omega_H}} VsigVo=1+ωHsAM
这里:
ωH=ω0=1CinRsig′\omega_H = \omega_0 = \frac{1}{C_{in}R_{sig}'} ωH=ω0=CinRsig′1
fH=12πCinRsig′f_H = \frac{1}{2\pi C_{in}R_{sig}'} fH=2πCinRsig′1
最后我们发现CS放大器的高频响应可以等效为一个低通型RC网络的高频响应:
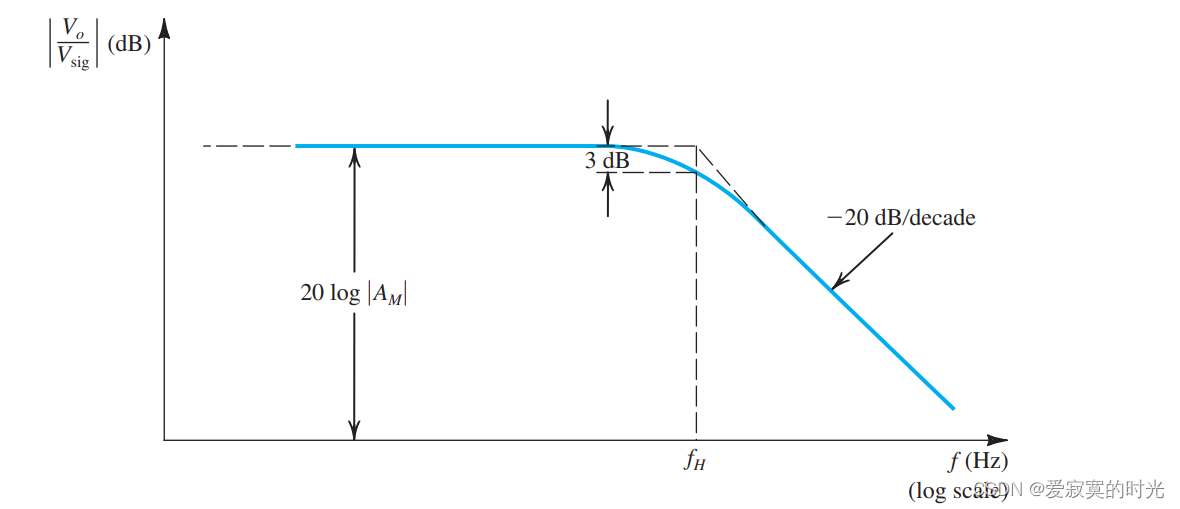
总结如下:
- 我们发现 fHf_HfH 反比于 Rsig′≃RsigR_{sig}' \simeq R_{sig}Rsig′≃Rsig 这说明信号源内阻越大, fHf_HfH 越小。
- 我们发现尽管 CgdC_{gd}Cgd 比较小,但是乘完因子之后 CeqC_{eq}Ceq 却很大,所以 CeqC_{eq}Ceq 称为了贡献 CinC_{in}Cin 的主要因素,所以越大的 CeqC_{eq}Ceq 则会造成 fHf_HfH 越小。
- 这给我们一个扩宽放大器带宽的一个思路,就是尽量降低米勒效应。
- 上述分析都是一种估计分析,也就是说 IgdI_{gd}Igd 必须非常小,并且频率也不能超过 fHf_HfH 太多。一个精准的分析应该是具有两个极点,其极点频率远大于 fHf_HfH 并且有两个传输零点分别是 s=∞s = \inftys=∞ 和 s=gm/Cgds = g_m / C_{gd}s=gm/Cgd 都是远大于 fHf_HfH 的,因此在只估计 fHf_HfH 的时候,以上因素均可以忽略。同时,这个方法指出影响放大器高频响应的关键因素:米勒效应。
- CS放大器在高频具有主导频率 fP≃fHf_P \simeq f_HfP≃fH 。
CE放大器
下图展示了CE放大器的高频等效模型:
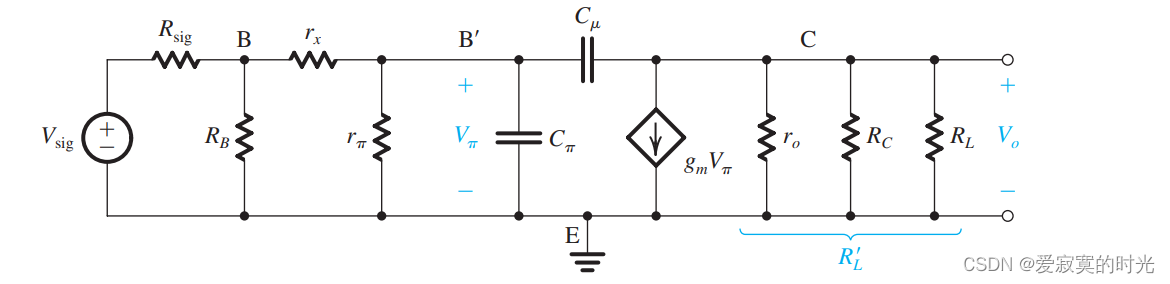
同样的我们进行戴维南等效:
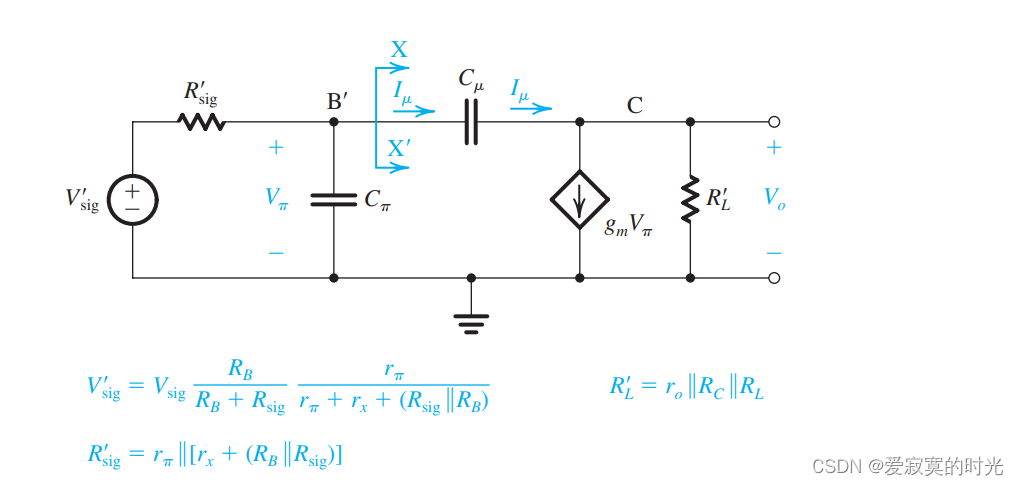
则此时原始的电压增益为:
AM=VoVsig=−RBRB+Rsigrπrπ+rx+(Rsig∣∣RB)(gmRL′)A_M = \frac{V_o}{V_{sig}} = -\frac{R_B}{R_B + R_{sig}}\frac{r_\pi}{r_\pi + r_x + (R_{sig} || R_B)}(g_m R_L') AM=VsigVo=−RB+RsigRBrπ+rx+(Rsig∣∣RB)rπ(gmRL′)
我们发现上面的电路图和MOS情况的完全一致,因此可以得到:
VoVsig=AM1+sωH\frac{V_o}{V_{sig}} = \frac{A_M}{1 + \frac{s}{\omega_H}} VsigVo=1+ωHsAM
这里:
fH=12πCinRsig′f_H = \frac{1}{2 \pi C_{in} R_{sig}'} fH=2πCinRsig′1
如图:
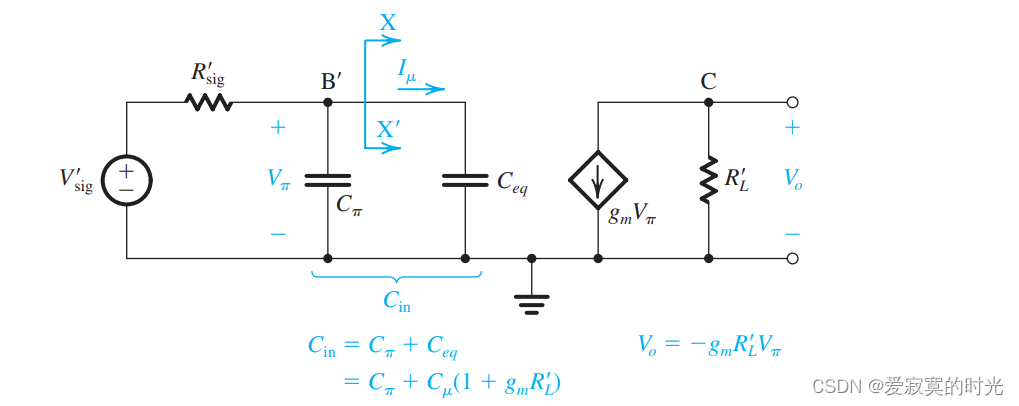
高频响应为:
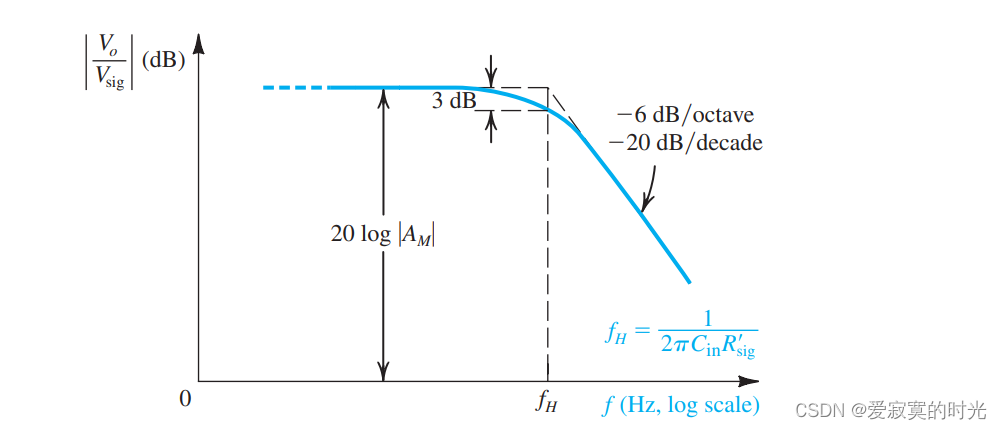
结论和MOS完全相似。
米勒定理
在我们上述的分析中,我们使用等效的 CeqC_{eq}Ceq 代替了桥电容 CgsC_{gs}Cgs 或是 CμC_\muCμ 。这是一个非常快速且有效的方法,我们称为 米勒定理 。
考虑下面的情况:
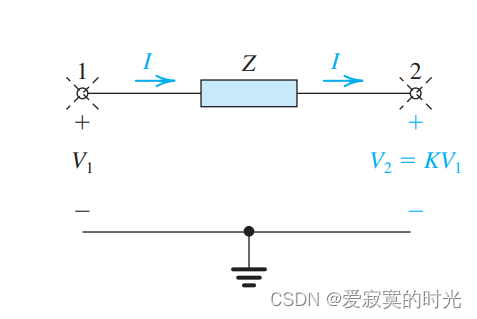
这是一个简化的二端传输网络,端口1和2为电气连接点,中间的阻抗为 ZZZ 。并且我们假设存在电压关系:
V2=KV1V_2 = KV_1 V2=KV1
米勒定理阐述阻抗 ZZZ 能够被等效替代成两个对地阻抗 Z1Z_1Z1 和 Z2Z_2Z2 ,称为米勒等效电路,如图:
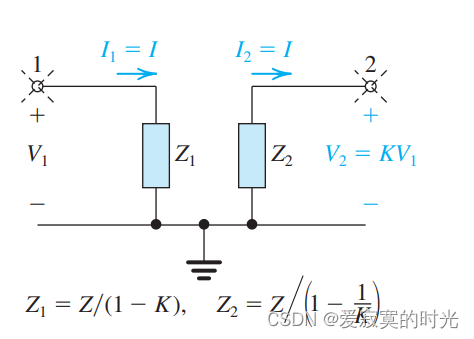
其中:
Z1=Z/(1−K)Z_1 = Z/(1 - K) Z1=Z/(1−K)
Z2=Z/(1−1K)Z_2 = Z / (1 - \frac{1}{K}) Z2=Z/(1−K1)
若要证明这个定理,我们必须保证电流关系不变,对于端口1来说:
I1=V1Z1=I=V1−KV1ZI_1 = \frac{V_1}{Z_1} = I = \frac{V_1 - KV_1}{Z} I1=Z1V1=I=ZV1−KV1
同样的对于端口2:
I2=0−V2Z2=0−KV1Z2=I=V1−KV1ZI_2 = \frac{0 - V_2}{Z_2} = \frac{0 - KV_1}{Z_2} = I = \frac{V_1 - KV_1}{Z} I2=Z20−V2=Z20−KV1=I=ZV1−KV1
我们发现,使用米勒等效替代之后,我们在输入端获得了一个和 1−K1-K1−K 有关的一个负反馈电阻,负反馈因子 1−K1-K1−K 我们称为 米勒因子 。
最后一点,我们在上面分析CS和CE的过程中,我们忽略了等效的输出电容,因为它实在是太小了 ≃Cgd\simeq C_{gd}≃Cgd 。
CS放大器在低 RsigR_{sig}Rsig 时候的的频率响应
有时候,CS放大器的信号源的内阻可能很小,此时的 fHf_HfH 的最大值限制不再受信号源的内阻的影响,如图:
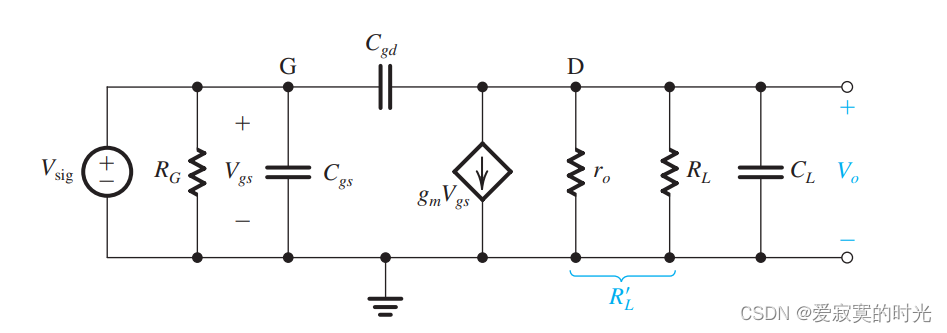
上图中信号源的内阻为零,而且我们在输出端引入了负载电容 CLC_LCL ,负载电容可能由负载自身的容性阻抗或是MOS的 CdbC_{db}Cdb 或是线间电容等等。之前,我们忽略了 CLC_LCL 是因为 fHf_HfH 的最大值主要受 RsigR_{sig}Rsig 影响。
注意到:
Vgs=VsigV_{gs} = V_{sig} Vgs=Vsig
Igd=sCgd(Vgs−Vo)I_{gd} = sC_{gd}(V_{gs} - V_o) Igd=sCgd(Vgs−Vo)
根据输出节点的电流方程:
Igd=gmVgs+VoRL′+sCLVoI_{gd} = g_mV_{gs} + \frac{V_o}{R_L'}+sC_LV_o Igd=gmVgs+RL′Vo+sCLVo
联立方程得到:
VoVsig=−gmRL′1−s(Cgd/gm)1+s(CL+CgdRL′)\frac{V_o}{V_{sig}} = -g_mR_L' \frac{1 - s(C_{gd}/g_m)}{1 + s(C_L + C_{gd}R_L')} VsigVo=−gmRL′1+s(CL+CgdRL′)1−s(Cgd/gm)
我们发现其存在一个零点频率:
fZ=gm2πCgdf_Z = \frac{g_m}{2 \pi C_{gd}} fZ=2πCgdgm
极点频率:
fH=12π(CL+Cgd)RL′f_H = \frac{1}{2 \pi (C_L + C_{gd})R_L'} fH=2π(CL+Cgd)RL′1
为了说明极点是怎么形成的,我们可以观察下图,下图中,我们将电压源置零。
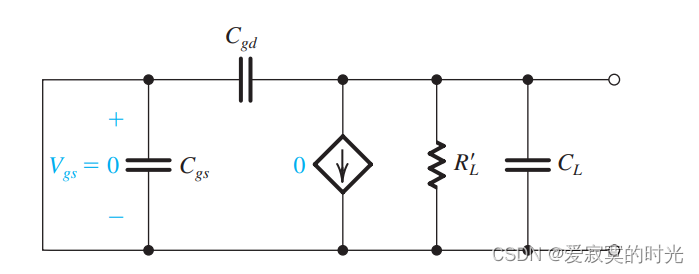
此时 RL′R_L'RL′ 可以观察到的电容为 CL+CgdC_L + C_{gd}CL+Cgd 。
我们发现传输零点频率要比 fHf_HfH 大很多:
fZfH=(gmRL′)(1+CLCgd)\frac{f_Z}{f_H} = (g_m R_L')(1 + \frac{C_L}{C_{gd}}) fHfZ=(gmRL′)(1+CgdCL)
因此传输零点一般不影响高频响应。实际上,我们知道,大约从 fHf_HfH 开始,增益 ∣AM∣|A_M|∣AM∣ 将以 -6dB每八度或-20dB每十倍的速度下降,存在一个假设的理想零点(单位增益) ftf_tft ,如图:
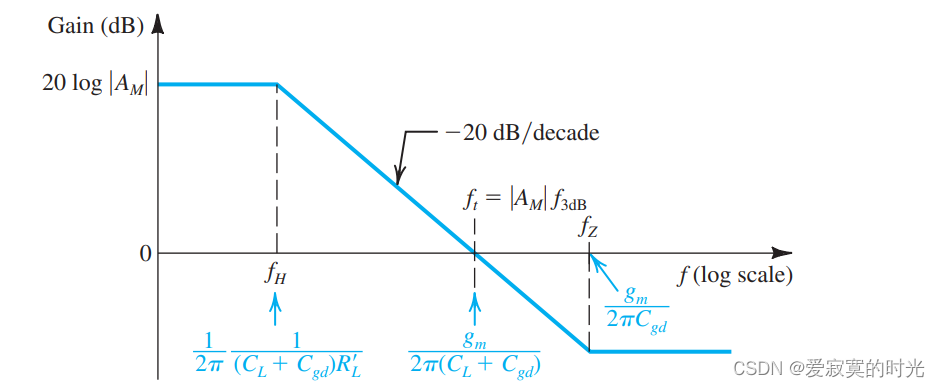
我们可以计算出:
ft=∣AM∣fHf_t = |A_M|f_H ft=∣AM∣fH
其值等于 增益-带宽积 。
进而:
ft=gmRL′12π(CL+Cgd)RL′=gm2π(CL+Cgd)f_t = g_mR_L'\frac{1}{2 \pi (C_L + C_{gd})R_L'} = \frac{g_m}{2 \pi (C_L + C_{gd})} ft=gmRL′2π(CL+Cgd)RL′1=2π(CL+Cgd)gm
这说明,当频率超过 ftf_tft 其增益衰减到几乎为0dB。
相关文章:

电子技术——CS和CE放大器的高频响应
电子技术——CS和CE放大器的高频响应 在绘制出MOS和BJT的高频响应模型之后,我们对MOS和BJT的高频响应有了进一步的认识。现在我们想知道的是在高频响应中 fHf_HfH 的关系。 高频响应分析对电容耦合还是直接耦合都是适用的,因为在电容耦合中高频模式下…...

2023年数学建模美赛D题(Prioritizing the UN Sustainability Goals):SDGs 优先事项的选择
正在写,不断更新,别着急。。。 4. SDGs 优先事项的选择 4.1 基于SDG密度分布图选择优先事项 虽然每个可持续发展目标的接近度矩阵和中心性度量的结果是通用的,并创建了基本的可持续发展目标网络,但由于各国在网络的不同部分取得…...

springboot实现项目启动前的一些操作
在服务启动时,做一些操作,比如加载配置,初始化数据,请求其他服务的接口等。 有三种方法: 第一种是实现CommandLineRunner接口 第二种是实现ApplicationRunner接口 第三种是使用注解:PostConstruct 三者使用…...

详解JavaScript的形参,实参以及传参
文章目录 前言一、参数是什么?二、形参和实参 1.形参 2.实参三、传参 1.参数传递的对应关系2.两个传参的例子 总结前言 编程初学者在接触JavaScript这门语言时,很难搞懂里面的逻辑,这就会导致入门慢,入门难。这种难度一般…...

Vue中的diff算法
diff算法介绍 diff算法是一种高效对比算法。diff算法在组件更新即响应式数据监控到数据的改变,重新生成虚拟DOM树的时候调用,然后通过diff算法计算出前后虚拟dom树的差异点,更新dom时只更新变化的部分。 直接比较和修改两个数的复杂度为什么…...

【面试题】前端春招第二面
不容错过的一些面试题小细节,话不多说,直接看题~大厂面试题分享 面试题库后端面试题库 (面试必备) 推荐:★★★★★地址:前端面试题库HTML/CSS/Javascript/ES篇(1)标准盒模型和怪异盒…...
Pytorch 基础之张量数据类型
学习之前:先了解 Tensor(张量) 官方文档的解释是: 张量如同数组和矩阵一样, 是一种特殊的数据结构。在PyTorch中, 神经网络的输入、输出以及网络的参数等数据, 都是使用张量来进行描述。 说白了就是一种数据结构 基本数据类型…...
Java 基础面试题——常见类
目录1.String 为什么是不可变的?2.字符串拼接用“” 和 StringBuilder 有什么区别?3.String、StringBuffer 和 StringBuilder 的区别是什么?4.String 中的 equals() 和 Object 中的 equals() 有何区别?5.Object 类有哪些常用的方法?6.如何获…...

Windows 系统从零配置 Python 环境,安装CUDA、CUDNN、PyTorch 详细教程
文章目录1 配置 python 环境1.1 安装 Anaconda1.2 检查环境安装成功1.3 创建虚拟环境1.4 进入/退出 刚刚创建的环境1.5 其它操作1.5.1 查看电脑上所有已创建的环境1.5.2 删除已创建的环境2 安装 CUDA 和 CUDNN2.1 查看自己电脑支持的 CUDA 版本2.2 安装 CUDA2.3 安装 CUDNN2.4 …...
[REDIS]redis的一些配置文件
修改配置文件 vim /etc/redis/redis.conf目录 protected-mode tcp-backlog timeout tcp-keepalive daemonize pidfile loglevel databases 设置密码 maxclients maxmemory maxmemory-policy maxmemory-samples 默认情况下 bind127.0.0.1 只能接受本机的访问请求。在不写的情况…...

Java反序列化漏洞——CommonsCollections4.0版本—CC2、CC4
一、概述4.0版本的CommonsCollections对之前的版本做了一定的更改,那么之前的CC链反序列化再4版本中是否可用呢。实际上是可用的,比如CC6的链,引入的时候因为⽼的Gadget中依赖的包名都是org.apache.commons.collections ,⽽新的包…...

下载网上压缩包(包含多行json)并将其转换为字典的解决方案
大家好,我是爱编程的喵喵。双985硕士毕业,现担任全栈工程师一职,热衷于将数据思维应用到工作与生活中。从事机器学习以及相关的前后端开发工作。曾在阿里云、科大讯飞、CCF等比赛获得多次Top名次。喜欢通过博客创作的方式对所学的知识进行总结与归纳,不仅形成深入且独到的理…...

【郭东白架构课 模块一:生存法则】11|法则五:架构师为什么要关注技术体系的外部适应性?
你好, 我是郭东白。 前四条法则分别讲了目标、资源、人性和技术周期,这些都与架构活动的外部环境有关。那么今天我们来讲讲在架构活动内部,也就是在架构师可控的范围内,应该遵守哪些法则。今天这节课,我们就先从技术体…...

Mindspore安装
本文用于记录搭建昇思MindSpore开发及使用环境的过程,并通过MindSpore的API快速实现了一个简单的深度学习模型。 什么是MindSpore? 昇思MindSpore是一个全场景深度学习框架,旨在实现易开发、高效执行、全场景覆盖三大目标。 安装步骤 鉴于笔者手头硬…...

C++010-C++嵌套循环
文章目录C010-C嵌套循环嵌套循环嵌套循环举例题目描述 输出1的个数题目描述 输出n行99乘法表题目描述 求s1!2!...10!作业在线练习:总结C010-C嵌套循环 在线练习: http://noi.openjudge.cn/ https://www.luogu.com.cn/ 嵌套循环 循环可以指挥计算机重复去…...
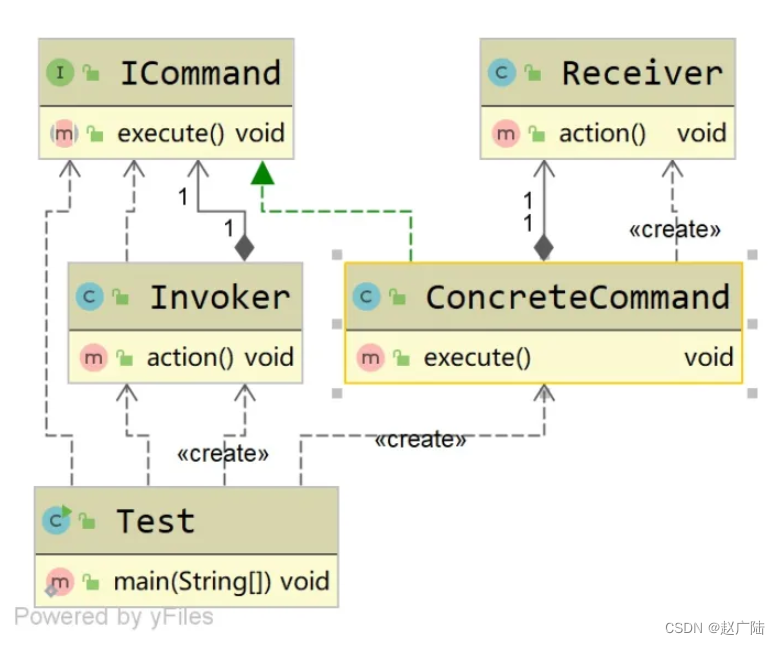
设计模式之迭代器模式与命令模式详解和应用
目录1 迭代器模式1.1 目标1.2 内容定位1.3 迭代器模式1.4 迭代器模式的应用场景1.5 手写字定义的送代器1.6 迭代器模式在源码中的体现1.7 迭代器模式的优缺点2 命令模式2.1 定义2.2 命令模式的应用场景2.3 命令模式在业务场景中的应用2.4 命令模式在源码中的体现2.5 命令模式的…...

【QA】[Vue/复选框全选] v-model绑定每一项的赋初值问题
发生场景:不只是复选框的状态改变,还有的功能要用到复选框的选中状态,比如:购物车计算总价,合计等等。 引入:复选框 checkbox 在使用时,需要用v-model绑定布尔值,来获取选中状态&…...
python基于django+vue微信小程序的校园二手闲置物品交易
在大学校园里,存在着很多的二手商品,但是由于信息资源的不流通以及传统二手商品信息交流方式的笨拙,导致了很多仍然具有一定价值或者具有非常价值的二手商品的囤积,乃至被当作废弃物处理。现在通过微信小程序的校园二手交易平台,可以方便快捷的发布和交流任何二手商品的信息,并…...

设计模式之观察者模式
什么是观察者模式 观察者模式定义了对象之间一种一对多依赖关系,使得每当一个对象状态发生改变时,其相关依赖对象都能收到通知并自动刷新。 观察者模式主要包含以下几个角色: Subject(目标):指被观察的对…...

Java Lambda表达式
目录1 Lambda表达式1.1 函数式编程思想概括1.2 Lambda表达式标准格式1.3 Lambda表达式练习1(抽象方法无参无返回值)1.4 Lambda表达式练习2(抽象方法带参无返回值)1.5 Lambda表达式练习2(抽象方法带参带返回值ÿ…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

如何更改默认 Crontab 编辑器 ?
在 Linux 领域中,crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用,用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益,允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...

uniapp 小程序 学习(一)
利用Hbuilder 创建项目 运行到内置浏览器看效果 下载微信小程序 安装到Hbuilder 下载地址 :开发者工具默认安装 设置服务端口号 在Hbuilder中设置微信小程序 配置 找到运行设置,将微信开发者工具放入到Hbuilder中, 打开后出现 如下 bug 解…...
