源码解析Collections.sort ——从一个逃过单测的 bug 说起
本文从一个小明写的bug 开始,讲bug的发现、排查定位,并由此展开对涉及的算法进行图解分析和源码分析。
事情挺曲折的,因为小明的代码是有单测的,让小明更加笃定自己写的没问题。所以在排查的时候,也经历了前世的500年,去排查排序后的list改动(主要是小明和同事互相怀疑对方的代码,不多说了)。
本文从问题定位之后开始讲:

前言
小明写了一个自定义排序的代码,简化后如下。聪明的你快来帮小明review一下吧。
代码
背景:有一批休息室,status是状态,其中1表示空闲,8表示使用中,2表示在维修。需要按照1空闲<8使用中<2在维修的顺序进行排序。
例如:输入:[1,8, 2, 2, 8, 1, 8],期望输出:[1, 1, 8, 8, 8, 2, 2]。list不为空,数量小于100。
环境:JDK 8
小明的代码如下:
/**
* 排序
*/
private static int compare(Integer status1, Integer status2) {// 1<8<2 ,按照这样的规则排序if (status2 != null && status1 != null) {// 2-维修中, 维修中排到最后面if (status2.equals(2)) {return -1;} else {// 8-使用中, 排在倒数第二,仅在维修中之前if (status2.equals(8) && !status1.equals(2)) {return -1;}}}return 0;}//Test public static void main(String[] args) {List<Integer> list = Lists.newArrayList(1, 8, 2, 2, 8, 1, 8);System.out.println("排序前:"+list);list.sort(Test::compare);System.out.println("排序后:"+list);}看上面的代码有问题么?别急,咱们先给个入参试一下。
测试
[ 1, 8, 2, 2, 8, 1, 8 ]
public static void main(String[] args) {List<Integer> list = Lists.newArrayList(1, 8, 2, 2, 8, 1, 8);System.out.println("排序前:"+list);list.sort(Test::compare);System.out.println("排序后:"+list);}输出:
排序前:[1, 8, 2, 2, 8, 1, 8]
排序后:[1, 1, 8, 8, 8, 2, 2]结论:结果是对的,符合预期 。 ( 按照1空闲<8使用中<2维修中的顺序进行排序) 。
嗯,看起来排序是对的。但确实是有问题呢?
(小明OS :哪里有问题?不可能有问题!我本地是好的!)

那我们看看情景复现👉🏻
情景复现
那有什么问题呢?我们再给几个入参试一下 。
case1 : 随机入参
[2, 8, 1, 2, 8, 8, 8, 2, 1]
输出:
排序前:[2, 8, 1, 2, 8, 8, 8, 2, 1]
排序后:[1, 1, 8, 8, 8, 8, 2, 2, 2]
期望是:[1, 1, 8, 8, 8, 8, 2, 2, 2]结论:结果对,符合预期 ✅。
case2 : 多增加一些数
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 8, 2, 2]
输出:
排序前:[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 8, 2, 2]
排序后:[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 8, 2, 2]
期望是:[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 8, 2, 2, 2, 2, 2, 2, 2]结论:结果不对了,不符合预期 ❌。
case3 : 换几个数
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 8, 8, 8, 8, 8, 2, 2, 2, 2, 2, 8, 8, 8, 8, 2, 2]
输出:
排序前:[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 8, 8, 8, 8, 8, 2, 2, 2, 2, 2, 8, 8, 8, 8, 2, 2]
排序后:[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 8, 8, 8, 8, 8, 8, 8, 8, 8, 2, 2, 2, 2, 2, 2, 2]
期望是:[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 8, 8, 8, 8, 8, 8, 8, 8, 8, 2, 2, 2, 2, 2, 2, 2]结论:结果又对了??

这是什么情况?!

小明有些慌了,越想越觉得奇怪,目前看起来有这样几个看起来些许离谱的结论:
1、可能是和数据量有关系(因为用32位以下的数据,多次Test 也没发现问题),
2、一定和数据数值有关系。(32位以上,有的数据样本没问题,有的有问题)。
3、有问题都在中间部分,而两边是有序的,猜测像排序归并导致的问题。
定位
想查这个问题,小明有三个思路。
一是:代码的逻辑比较,是有一些不完整的。那可以先试着改改代码,通过这几个失败用例,然后在找深层原因。
二是:查查用的排序类,有没有坑。用法有没有特殊注意的,有没有类似的案例。
三是:从源码上,理清排序底层的逻辑,找到哪一个环节排序出了问题。
顺着这三个思路,小明发现写的代码里缺少返回为1的场景。虽然小明不知道有没有影响,但是试了试,发现好使。。但为啥呢?
private static int compare(Integer status1, Integer status2) {// 1<8<2 ,按照这样的规则排序if (status2 != null && status1 != null) {// 2-维修中, 维修中排到最后面if (status2.equals(2)) {return -1;} else {// 8-使用中, 排在倒数第二,仅在维修中之前if (status2.equals(8) && !status1.equals(2)) {return -1;}else{return 1;}}}return 0;}}然后小明看 Collections.sort 的坑,没有看到和这个相关的。
接下来,还是要来调试代码。最终定位是因为原来的compare 自定义代码里,对 compaer(2,1) 这种应该返回1的情况 ,默认返回了0。导致在底层两组数据归并排序过程,误以为1和2相等了。
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 8, 2, 2]
见Debug部分:(具体分析内容在后边源码部分)

解决方案
发现问题,就好解决了。方案是,要么补充完善逻辑,要么换用一种权重映射的排序方式。
1 优化代码
/**
* 按照1<8<2排序
**/
private static int compare(Integer status1, Integer status2) {// 2大于8 大于1 ,按照这样的规则排序if (status2 != null && status1 != null) {// 2-维修中, 维修中排到最后面if (status2.equals(2)) {return -1;} else {// 8-使用中, 排在倒数第二,仅在维修中之前if (status2.equals(8) && !status1.equals(2)) {return -1;}else{return 1;}}}return 0;}2 改为权重等方式排序
当然,还有对于一些容易理解出错的排序,也可以通过设置权重映射的方式进行排序。
小明忽然想起来,无论底层排序算法是什么, 排序逻辑还是要完整。这一点也开发规约也是有的呀。👉🏻
【注意】在JDK7版本及以上,为了让Arrays.sort、Collections.sort正常工作,Comparator必须满足以下三个条件,否则会抛出IllegalArgumentException异常。
1)比较x和y的结果应该与比较y和x的结果相反。
2)如果x>y,y>z,则x>z。
3)如果x=y,则比较x和z的结果应该与比较y和z的结果相同。
好了问题解决了,那我们接下来慢慢聊聊这里Collections.sort 底层用的TimSort排序原理。以及为什么32位及以上才有问题,为什么正好是归并过程有问题 ?
源码解读
JAVA 7 中集合类中的sort 开始,默认用TimSort排序方法 。Tim Sort,里的Tim 也没什么特别的含义。Tim是这个算法的创始人Tim Peters 的名字。该算法首先在Python中应用,之后在 java 中应用。
TimSort :一种稳定的、自适应的、迭代的归并排序,在部分排序数组上运行时需要的比较远远少于nlg (n)次,而在随机数组上运行时提供与传统归并排序相当的性能。像所有合适的归并排序一样,这种排序是稳定的,运行时间为O(n log n)(最坏情况)。在最坏的情况下,这种排序需要n/2个对象引用的临时存储空间;在最好的情况下,它只需要少量的常量空间。这个实现改编自Tim Peters的Python列表排序
图解 TimSort 排序原理
如果数组的长度小于32,直接采用二分法插入排序。(略)
如果数组的长度大于32,找到单调上升段(或下降段,进行反转),然后基于这个单调片段,通过插入排序的方式进行合并。如此反复归并相邻片段。
到这一步的时候,小明恍然大悟,怪不得32位数以下,没有出现过问题呢。
这个算法里有一个重要的概念,也可以理解为分段( 算法里 run )。每个分段都是连续上升或下降的子串

然后对下降的分段进行反转,使其变为一个递增的子串。这样就可以得到若干的分段,使得每个分段都单调递增,后续就可以对这些分段进行合并。

👉🏻 当然算法里会计算出一个最小的分段长度(Java里16-32之间),来控制分段的数量以保证效率。对那些不满足最小长度的分区,会采用二分插入的方法,使其满足最的长度。比如我们假设最小的长度是3,那此时由于第二段36 不符合最小长度3,会利用二分插入法,将8插入到第二段。即 368 就是第二段了。
分段划分之后,下一步就是如何进行合并。
合并时,会将分区进行压栈,并判断是否需要和之前的分段做合并。当然还有一些更详细的优化点,具体可看下文源码部分。重点说一下,两个分段如何进行合并。
假设以下内容:
第一个段包含元素:[1, 2, 3, 5, 6, 8, 9]
第二个段包含元素:[4, 6, 7, 8, 10, 11, 12]
第一个段在数组中出现在第二个段之前。请注意,实际段落长度不会这么短。如前所述,段落长度应介于16到32之间。此处只是提供示例以说明问题。
gallopRight():查找第二个段的第一个元素在第一个段中的位置。例如,在此示例中,位置为2。这意味着前两个元素不需要参与合并,它们的位置不需要改变。
gallopLeft():查找第一个段的最后一个元素在第二个段中的位置。在此处,发现第二个段中的第四个元素为10。因此,第二个段中的10、11、12不需要参与合并,它们的位置也不需要改变。

最终参与合并的段为:
第一段:[5,6,8,9]
第二段:[4, 6, 7, 8]
这样参与合并的段的长度就大大减小了。 这里就是我们上边问题出现的地方。在gallopLeft 方法里,
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2,2]
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 8, 2, 2]
查找第一个段的最后一个元素【2】在第二个段中的位置时,比较【2】和【1】时,得出了相等的结果。这有什么影响呢?因为数组分段是单调递增的,也就是说第一组里最后一个(最大的)数据2,和第二组里第一个(最小的)数据1 相等。那也就是说,第一个数组直接在第二个数组之前。即:
[**1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2,**1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 8, 2, 2]
源码解读:Collections.sort 排序原理
入口
list.sort(Test::compare);
进入list sort
public void sort(Comparator<? super E> c) {final int expectedModCount = modCount; // 当前 modCount 的值Arrays.sort((E[]) elementData, 0, size, c); // 使用 Arrays.sort 对 elementData 数组进行排序if (modCount != expectedModCount) { // 检查排序过程中是否发生了并发修改throw new ConcurrentModificationException();}modCount++; // 增加 modCount 的值,表示进行了一次修改
}Arrays.sort()
进入Arrays.sort()方法
public static <T> void sort(T[] a, int fromIndex, int toIndex, Comparator<? super T> c) {if (c == null) {sort(a, fromIndex, toIndex); // 如果比较器为 null,调用默认的排序方法} else {rangeCheck(a.length, fromIndex, toIndex); // 检查 fromIndex 和 toIndex 的范围是否合法if (LegacyMergeSort.userRequested)legacyMergeSort(a, fromIndex, toIndex, c); // 如果指定使用传统的归并排序,则调用该方法elseTimSort.sort(a, fromIndex, toIndex, c, null, 0, 0); // 否则,调用 TimSort 进行排序}
}TimSort.sort
我们重点看 TimSort.sort
/*** Sorts the given range, using the given workspace array slice* for temp storage when possible. This method is designed to be* invoked from public methods (in class Arrays) after performing* any necessary array bounds checks and expanding parameters into* the required forms.** @param a the array to be sorted* @param lo the index of the first element, inclusive, to be sorted* @param hi the index of the last element, exclusive, to be sorted* @param c the comparator to use* @param work a workspace array (slice)* @param workBase origin of usable space in work array* @param workLen usable size of work array* @since 1.8*/static <T> void sort(T[] a, int lo, int hi, Comparator<? super T> c,T[] work, int workBase, int workLen) {assert c != null && a != null && lo >= 0 && lo <= hi && hi <= a.length;int nRemaining = hi - lo;if (nRemaining < 2)return; // 数组长度为 0 或 1 时,无需排序// 如果数组长度较小,执行“迷你的 TimSort”而不进行合并操作if (nRemaining < MIN_MERGE) {int initRunLen = countRunAndMakeAscending(a, lo, hi, c);binarySort(a, lo, hi, lo + initRunLen, c);return;}/*** 从左到右遍历数组一次,找到自然的 run,* 将短的自然 run 扩展到 minRun 的长度,并合并 run 以保持栈的不变性。*/TimSort<T> ts = new TimSort<>(a, c, work, workBase, workLen);int minRun = minRunLength(nRemaining);do {// 确定下一个 runint runLen = countRunAndMakeAscending(a, lo, hi, c);// 如果 run 很短,则扩展到 min(minRun, nRemaining) 的长度if (runLen < minRun) {int force = nRemaining <= minRun ? nRemaining : minRun;binarySort(a, lo, lo + force, lo + runLen, c);runLen = force;}// 将 run 推入待处理 run 栈,并可能进行合并ts.pushRun(lo, runLen);ts.mergeCollapse();// 前进以找到下一个 runlo += runLen;nRemaining -= runLen;} while (nRemaining != 0);// 合并所有剩余的 run 以完成排序assert lo == hi;ts.mergeForceCollapse();assert ts.stackSize == 1;
}countRunAndMakeAscending : 找到数组中的一段有序数字
countRunAndMakeAscending:方法的主要作用就是找到数组中的一段有序数字,并告诉我们它们的长度。如果这段数字是倒序的,它还会将它们反转成正序。
private static <T> int countRunAndMakeAscending(T[] a, int lo, int hi, Comparator<? super T> c) {assert lo < hi;int runHi = lo + 1;if (runHi == hi)return 1;// 找到 run 的结束位置,并在降序情况下反转范围if (c.compare(a[runHi++], a[lo]) < 0) { // 降序while (runHi < hi && c.compare(a[runHi], a[runHi - 1]) < 0)runHi++;reverseRange(a, lo, runHi);} else { // 升序while (runHi < hi && c.compare(a[runHi], a[runHi - 1]) >= 0)runHi++;}return runHi - lo;
}mergeCollapse : 将连续的有序小段合并成更大的有序段
mergeCollapse的主要作用就是在排序过程中,将连续的有序小段合并成更大的有序段,以便更高效地进行排序。
/*** Examines the stack of runs waiting to be merged and merges adjacent runs* until the stack invariants are reestablished:* 检查等待合并的运行堆栈,并合并相邻的运行,直到满足堆栈条件:* 1. runLen[i - 3] > runLen[i - 2] + runLen[i - 1]* 2. runLen[i - 2] > runLen[i - 1]** This method is called each time a new run is pushed onto the stack,* so the invariants are guaranteed to hold for i < stackSize upon* entry to the method.* 每次将新的运行推入堆栈时,都会调用此方法,因此在进入方法时,对于 i < stackSize,满足堆栈条件。*/private void mergeCollapse() {while (stackSize > 1) {int n = stackSize - 2;if (n > 0 && runLen[n-1] <= runLen[n] + runLen[n+1]) {if (runLen[n - 1] < runLen[n + 1])n--;// 在位置 n 处合并相邻的运行mergeAt(n);} else if (runLen[n] <= runLen[n + 1]) {// 在位置 n 处合并相邻的运行mergeAt(n);} else {// 堆栈条件已满足,退出循环break;}}
}mergeAt(n) : 把两个有序的小段合并成一个更大的有序段
mergeAt(n):它帮助我们把两个有序的小段合并成一个更大的有序段,以便在排序过程中保持正确的顺序。
/*** Merges the two runs at stack indices i and i+1. Run i must be* the penultimate or antepenultimate run on the stack. In other words,* i must be equal to stackSize-2 or stackSize-3.** @param i stack index of the first of the two runs to merge*/
private void mergeAt(int i) {assert stackSize >= 2;assert i >= 0;assert i == stackSize - 2 || i == stackSize - 3;int base1 = runBase[i];int len1 = runLen[i];int base2 = runBase[i + 1];int len2 = runLen[i + 1];assert len1 > 0 && len2 > 0;assert base1 + len1 == base2;// 记录合并后的 run 长度;如果 i 是倒数第三个 run,也要滑动最后一个 run(不参与本次合并)runLen[i] = len1 + len2;if (i == stackSize - 3) {runBase[i + 1] = runBase[i + 2];runLen[i + 1] = runLen[i + 2];}stackSize--;// 找到 run2 中第一个元素在 run1 中的插入位置int k = gallopRight(a[base2], a, base1, len1, 0, c);assert k >= 0;base1 += k;len1 -= k;if (len1 == 0)return;// 找到 run1 中最后一个元素在 run2 中的插入位置len2 = gallopLeft(a[base1 + len1 - 1], a, base2, len2, len2 - 1, c);assert len2 >= 0;if (len2 == 0)return;// 使用临时数组(长度为 min(len1, len2))合并剩余的 runif (len1 <= len2)mergeLo(base1, len1, base2, len2);elsemergeHi(base1, len1, base2, len2);
}gallopRigth && gallopLeft :在有序数组中快速查找目标元素的可能位置,便于合并
其中两个主要的方法就是gallopRigth()和gallopLeft() 。这里就是上面所说的 找元素的部分。
主要作用就是在有序数组中快速查找目标元素的可能位置,它采用一种跳跃式的查找策略,通过快速定位可能的位置,提高查找速度。
也就是上文中这一部分:
假设以下内容:
第一个段包含元素:[1,2,3,5,6,8,9]
第二个段包含元素:[4,6,7,8,10,11,12]第一个段在数组中出现在第二个段之前。请注意,实际段落长度不会这么短。如前所述,段落长度应介于16到32之间。此处只是提供示例以说明问题。
gallopRight():查找第二个段的第一个元素在第一个段中的位置。例如,在此示例中,位置为2。这意味着前两个元素不需要参与合并,它们的位置不需要改变。gallopLeft():查找第一个段的最后一个元素在第二个段中的位置。在此处,发现第二个段中的第四个元素为10。因此,第二个段中的10、11、12不需要参与合并,它们的位置也不需要改变。
这样参与合并的段的长度就大大减小,时间相应的就变短了(算法的优化点之一)。gallopLeft 代码如下:
gallopLeft方法用于在有序数组的指定范围内进行快速查找,定位将指定键插入的位置或最左边相等元素的索引。它使用跳跃式的查找策略,根据键与范围内元素的比较结果,通过不断调整步长进行左跳或右跳,直到找到合适的插入位置。最后,使用二分查找在找到的范围内确定确切的插入位置,并返回结果。这个方法的目标是提高查找效率。
/*** Locates the position at which to insert the specified key into the* specified sorted range; if the range contains an element equal to key,* returns the index of the leftmost equal element.** @param key 要搜索插入位置的键* @param a 要搜索的数组* @param base 范围内第一个元素的索引* @param len 范围的长度;必须大于 0* @param hint 开始搜索的索引,0 <= hint < n。hint 越接近结果,该方法的执行速度越快。* @param c 用于对范围进行排序和搜索的比较器* @return 整数 k,0 <= k <= n,满足 a[b + k - 1] < key <= a[b + k],* 假设 a[b - 1] 是负无穷大,a[b + n] 是正无穷大。* 换句话说,键属于索引 b + k 处;或者换句话说,* 数组 a 的前 k 个元素应该在键之前,后面的 n - k 个元素应该在键之后。*/
private static <T> int gallopLeft(T key, T[] a, int base, int len, int hint,Comparator<? super T> c) {assert len > 0 && hint >= 0 && hint < len;int lastOfs = 0;int ofs = 1;if (c.compare(key, a[base + hint]) > 0) {// 向右跳跃,直到 a[base+hint+lastOfs] < key <= a[base+hint+ofs]int maxOfs = len - hint;while (ofs < maxOfs && c.compare(key, a[base + hint + ofs]) > 0) {lastOfs = ofs;ofs = (ofs << 1) + 1;if (ofs <= 0) // 检查 int 溢出ofs = maxOfs;}if (ofs > maxOfs)ofs = maxOfs;// 将偏移量相对于基准位置进行调整lastOfs += hint;ofs += hint;} else { // key <= a[base + hint]// 向左跳跃,直到 a[base+hint-ofs] < key <= a[base+hint-lastOfs]final int maxOfs = hint + 1;while (ofs < maxOfs && c.compare(key, a[base + hint - ofs]) <= 0) {lastOfs = ofs;ofs = (ofs << 1) + 1;if (ofs <= 0) // 检查 int 溢出ofs = maxOfs;}if (ofs > maxOfs)ofs = maxOfs;// 将偏移量相对于基准位置进行调整int tmp = lastOfs;lastOfs = hint - ofs;ofs = hint - tmp;}assert -1 <= lastOfs && lastOfs < ofs && ofs <= len;/** 现在 a[base+lastOfs] < key <= a[base+ofs],* 因此键位于 lastOfs 的右侧,但不超过 ofs 的位置。* 使用二分查找,在不变式 a[base + lastOfs - 1] < key <= a[base + ofs] 的条件下进行。*/lastOfs++;while (lastOfs < ofs) {int m = lastOfs + ((ofs - lastOfs) >>> 1);if (c.compare(key, a[base + m]) > 0)lastOfs = m + 1; // a[base + m] < keyelseofs = m; // key <= a[base + m]}assert lastOfs == ofs; // 所以 a[base + ofs - 1] < key <= a[base + ofs]return ofs;
}TimSort 算法的优缺点
优点
-
稳定性:TimSort 是一种稳定的排序算法,即相等元素的相对顺序在排序后保持不变。
-
高效的处理小规模或部分有序数组:TimSort 在处理小规模数组时具有良好的性能,可以利用插入排序的优势。此外,对于部分有序的数组,TimSort 也能快速识别并进行优化处理。
-
最坏情况下的时间复杂度是 O(n log n):在最坏情况下,TimSort 的时间复杂度与其他基于比较的排序算法(如快速排序和归并排序)相同,都是 O(n log n)。
-
适用于大多数实际数据:TimSort 是一种自适应的排序算法,它能够根据输入数据的特性进行优化,适应不同的数据分布和大小。
缺点
-
需要额外的空间:TimSort 在合并阶段需要额外的辅助空间,用于暂存部分数组。这可能导致空间复杂度较高,特别是对于大规模数据排序时。
-
对于某些特殊情况效率较低:在处理某些特殊情况下,例如完全逆序的数组。
最后:
通过查看 TimSort 的源码,可以深入了解该算法的工作原理、核心步骤和关键逻辑。这有助于我们对排查问题时快速定位问题,也有助于对算法的理解和知识的扩展。
另外 TimSort 是一种经过优化的排序算法,它采用了多种技巧来提高性能和效率。通过研究源码,我们可以学习到一些优化技巧,例如插入、二分查找的优化、自适应调整等。这些技巧或许可以用在我们日后的开发场景中。当然,最重要的还是去逐渐体会、借鉴其实现方式和设计优化思想。
最后的最后,谢谢小明。
小明:

以下是我收集到的比较好的学习教程资源,虽然不是什么很值钱的东西,如果你刚好需要,可以评论区,留言【777】直接拿走就好了


各位想获取资料的朋友请点赞 + 评论 + 收藏,三连!
三连之后我会在评论区挨个私信发给你们~
相关文章:

源码解析Collections.sort ——从一个逃过单测的 bug 说起
本文从一个小明写的bug 开始,讲bug的发现、排查定位,并由此展开对涉及的算法进行图解分析和源码分析。 事情挺曲折的,因为小明的代码是有单测的,让小明更加笃定自己写的没问题。所以在排查的时候,也经历了前世的500年…...

一周 AIGC 丨苹果下架多款 AIGC 应用,阿里云开源通义千问 70 亿参数模型
多个 AIGC 应用在苹果应用商店下架,包含数据采集和使用不够规范等问题。阿里云开源通义千问 70 亿参数模型,包括通用模型 Qwen-7 B 和对话模型 Qwen-7 B-Chat。腾讯混元大模型开始应用内测,内部多个业务线接入测试。百度智能云“千帆大模型平…...
tomcat虚拟主机配置演示
一.新建用于显示的index.jsp文件,写入内容 二.修改tomcat/apache-tomcat-8.5.70/conf/server.xml配置文件 匹配到Host那部分,按上面格式在后面添加自己的域名和文件目录信息 主要是修改name和docBase 保存退出重启tomcat,确保tomcat运行…...

Nacos基本应用
Nacos 基本应用 Nacos 提供了 SDK 和 OpenAPI 方式来完成服务注册与发现等操作,SDK 实际上是对于 http 请求的封装。 微服务架构的电子商务平台,其中包含订单服务、商品服务和用户服务。可以使用 Nacos 作为服务注册和发现的中心,以便各个微…...

UML的类图规则
public:号 private:-号 protected:#号类图多重关系: 泛化关系: 概念:也就是继承关系。表示方式:用带空心三角形的直线来表示。例子:动物和猫,人和老师关联关系: 概念:用于表示一类对…...

uniapp实现微信小程序长按二维码扫码加群或好友
<template><view><view class"tit">欢迎扫码加入</view><image show-menu-by-longpress"true" src"/static/img/qrcode/1.jpg" class"btn-icon" click"previewImage"></image></vie…...
)
轮转数组(每日一题)
“路虽远,行则将至” ❤️主页:小赛毛 ☕今日份刷题:轮转数组 题目链接:轮转数组 题目描述: 给定一个整数数组 nums,将数组中的元素向右轮转 k 个位置,其中 k 是非负数。 示例1: 输入…...
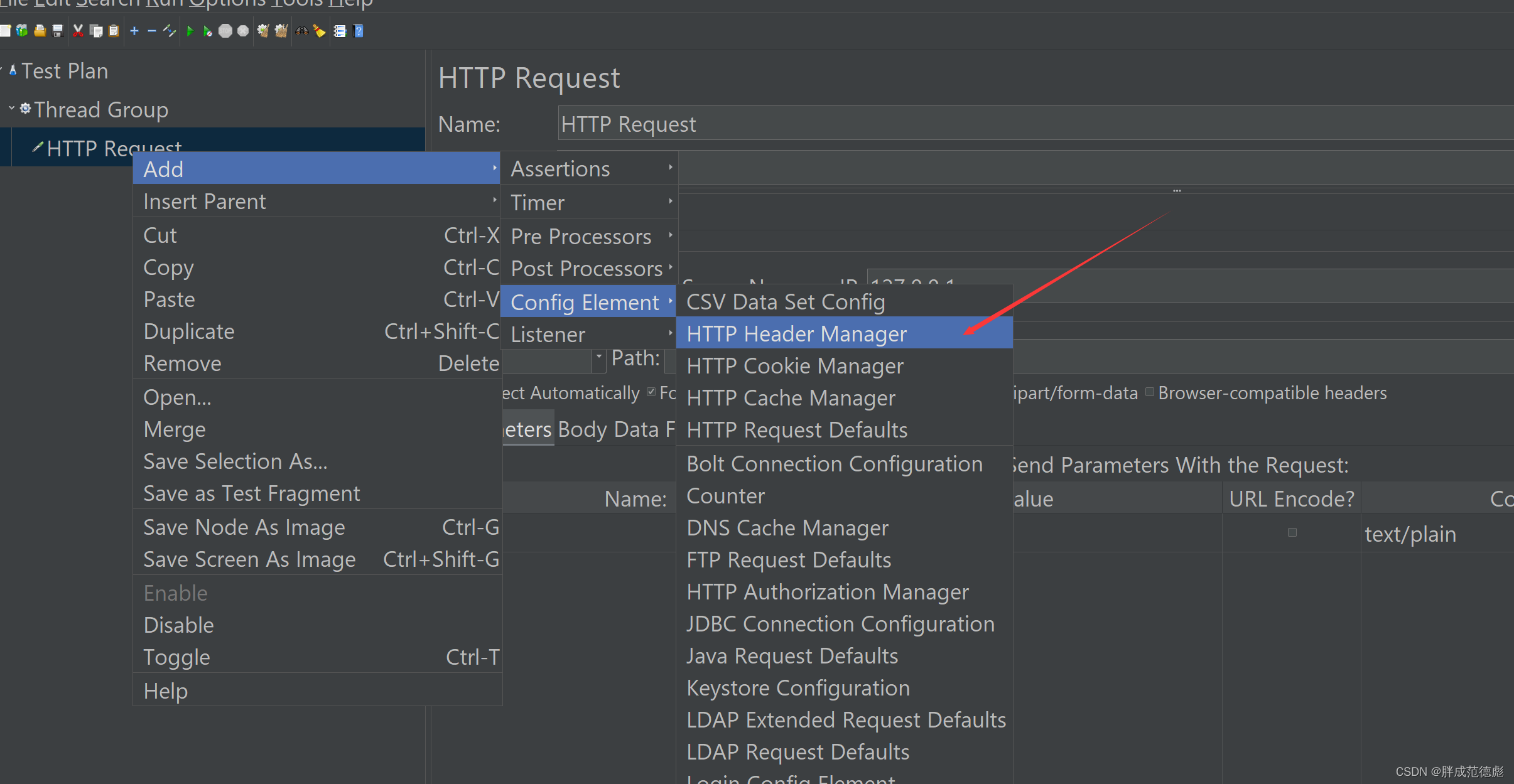
jmeter使用步骤
jmeter 使用步骤 1,进入jmeter目录中的bin目录,双击jmeter.bat 打开 2,右键test plan 创建线程组 3,配置线程组参数 4,右键刚刚创建的线程组,创建请求,填写请求地址 5,需要携带to…...

Ts中泛型的理解与使用
一、什么是泛型 在定义函数,定义接口或定义class类的时候,不先规定其类型,在使用的时候进行定义类型。 二、使用 1、定义函数: // 函数类型 function AA<T>(arg:T):T{return arg } AA<number>(1) AA<string>…...

uniapp使用eatchs雷达图
引入插件 <template><view class"page"><view class"AllBox"><view class"topTit">标题</view><view class"leftTit">对比分析</view><view class"tableBox"><view cl…...

PostgreSQL jsonb
PostgreSQL jsonb jsonb 函数以及操作符 在PostgreSQL中,有许多用于处理JSONB数据类型的内置函数和操作符。下面列出了一些常用的JSONB函数和操作符: jsonb_pretty(jsonb) 该函数将JSONB数据格式化为易读的多行字符串。jsonb_typeof(jsonb) 该函数返回…...

Spring系列四:AOP切面编程
文章目录 💗AOP-官方文档🍝AOP 讲解🍝AOP APIs 💗动态代理🍝初始动态代理🍝动态代理深入🍝AOP问题提出📗使用土方法解决📗 对土方法解耦-开发最简单的AOP类📗…...
VS+Qt+C++旅游景区地图导航源码实例
程序示例精选 VSQtC旅游景区地图导航 如需安装运行环境或远程调试,见文章底部个人QQ名片,由专业技术人员远程协助! 前言 这篇博客针对<<VSQtC旅游景区地图导航>>编写代码,代码整洁,规则,易读。…...
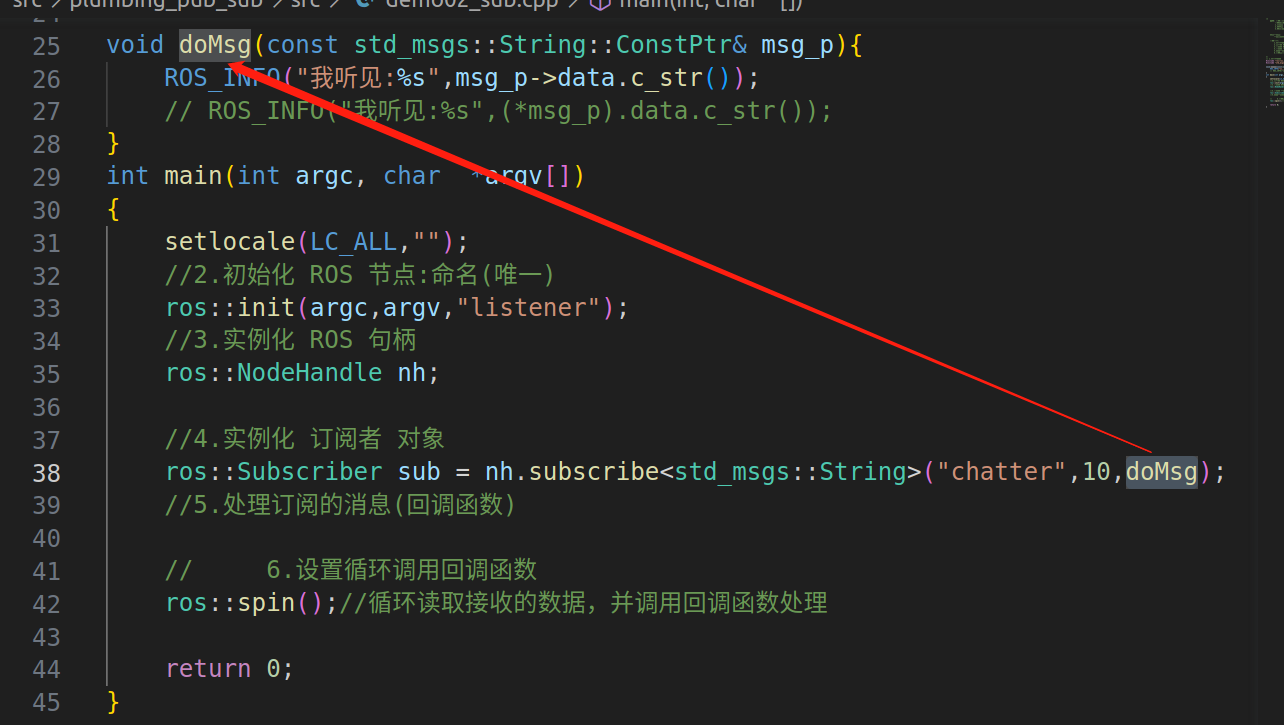
回调函数和一般函数的区别
回调函数:不是我能控制的,通过外界信号触发调用,例如下面是chatter 一般函数:我能控制的,顺序调用...
使用vite创建Vue/React前端项目,配置@别名和Sass样式,又快又方便
Vite官方网站:Vite | 下一代的前端工具链 Vite 并不是基于 Webpack 的,它有自己的开发服务器,利用浏览器中的原生 ES 模块。这种架构使得 Vite 比 Webpack 的开发服务器快了好几个数量级。Vite 采用 Rollup 进行构建,速度也更快…...
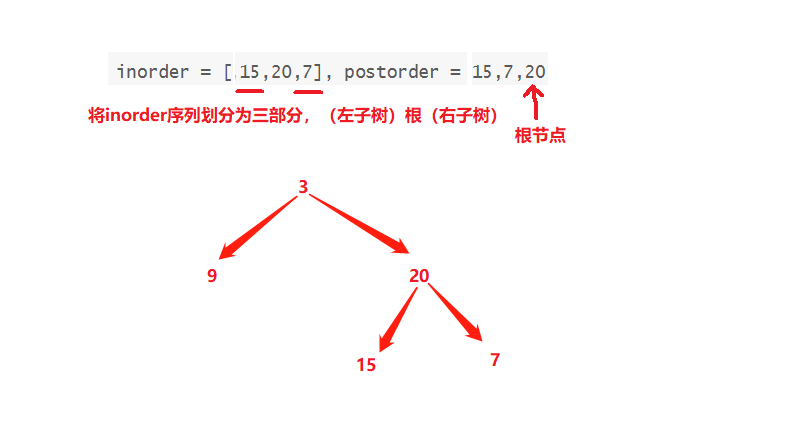
从前序与中序遍历序列构造二叉树,从中序与后序遍历序列构造二叉树
目录 从前序与中序遍历序列构造二叉树从中序与后序遍历序列构造二叉树 从前序与中序遍历序列构造二叉树 题目链接 给定两个整数数组 preorder 和 inorder ,其中 preorder 是二叉树的先序遍历, inorder 是同一棵树的中序遍历,请构造二叉树并返…...

【JS常见数据结构】
JS数据结构 前言数组JavaScript 中数组的常见操作:1. 创建数组:2. 访问数组元素:3. 插入元素:4. 删除元素:5. 查询元素: 链表单向链表双向链表循环链表 栈队列树二叉树示例 图图的定义图的分类图的表示方法…...

算法基础之插入排序
1、插入排序基本思想 插入排序的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。插入排序在实现上,通常采用in-place排序(即只需用到O(1)的额外空间的排序)&a…...

InfoQ 分享
...
Jupyter Notebook 遇上 NebulaGraph,可视化探索图数据库
在之前的《手把手教你用 NebulaGraph AI 全家桶跑图算法》中,除了介绍了 ngai 这个小工具之外,还提到了一件事有了 Jupyter Notebook 插件: https://github.com/wey-gu/ipython-ngql,可以更便捷地操作 NebulaGraph。 本文就手把手教你咋在 J…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...

