centos磁盘爆满可以清理mysql-bin.000011吗
`mysql-bin.000011` 是 MySQL 的二进制日志文件,用于记录数据库中的更改操作。删除该文件可能会导致数据库恢复、备份和复制等功能的中断或数据丢失。因此,在删除任何 MySQL 的二进制日志文件之前,请确保您了解其潜在影响并采取适当的备份措施。
在执行删除操作之前,可以通过以下步骤确认是否可以删除 `mysql-bin.000011` 文件:
- 登录到 MySQL 数据库,并查看当前的二进制日志列表:
mysql -u <username> -p
SHOW BINARY LOGS;
- 确保 `mysql-bin.000011` 文件不是当前活动日志,即没有被其他进程使用。活动日志的状态为 `File` 列标记为 `YES`:
SHOW MASTER STATUS;
如果 `mysql-bin.000011` 文件不是当前活动日志,且您确认不再需要该文件,可以通过以下命令删除它:
PURGE BINARY LOGS TO 'mysql-bin.000011';
请注意,上述操作将删除 `mysql-bin.000011` 文件及其之前所有的二进制日志文件,因此请谨慎操作,确保没有重要的数据需要保留。
相关文章:

centos磁盘爆满可以清理mysql-bin.000011吗
mysql-bin.000011 是 MySQL 的二进制日志文件,用于记录数据库中的更改操作。删除该文件可能会导致数据库恢复、备份和复制等功能的中断或数据丢失。因此,在删除任何 MySQL 的二进制日志文件之前,请确保您了解其潜在影响并采取适当的备份措施。…...
SSM个人博客项目
文章目录 SSM个人博客系统实现项目介绍 一、准备工作0. 创建项目添加对应依赖1. 数据库设计2. 定时实体类 二、功能实现1.统一功能处理统一返回格式统一异常处理定义登录拦截器 2. 注册登录实现生成获取验证码密码加盐实现注册功能登录功能注销功能 3.登录用户博客列表获取登录…...

vue插槽是什么?如何使用?
1、意义 插槽是vue提供的一个内置组件,是一个占位符。作用是可以向组件中传递一段html代码,加强了组件封装性以及复用性。 2、分类 插槽通常分为匿名插槽、具名插槽、作用域插槽 匿名插槽: 顾名思义就是没有名字的插槽,我们通…...

yum常用操作命令
目录 查询命令 查看当前所有仓库 检查可升级的程序 安装、卸载、升级 清除缓存命令 生成缓存 查询命令 列出已安装的软件包:yum list installed列出仓库中还未安装的软件包:yum list available列出指定软件包的依赖关系:yum deplist &…...
.Net C# 免费PDF合成软件
最近用到pdf合成,发现各种软件均收费啊,这个技术非常简单,别人写好的库一大把,这里用到了PDFsharp,项目地址Home of PDFsharp and MigraDoc Foundation 软件下载地址 https://download.csdn.net/download/g313105910…...
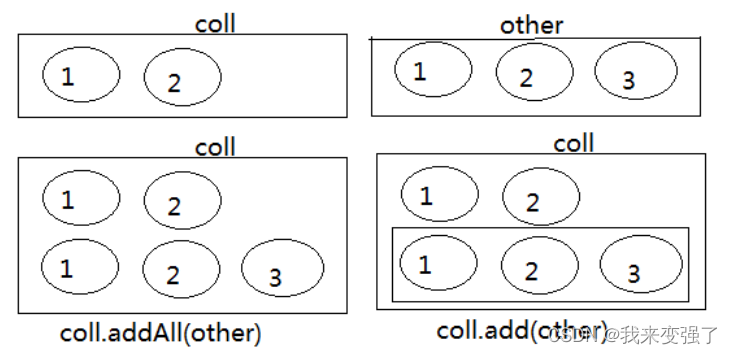
JAVA集合框架 一:Collection(LIst,Set)和Iterator(迭代器)
目录 一、Java 集合框架体系 1.Collection接口:用于存储一个一个的数据,也称单列数据集合(single)。 2.Map接口:用于存储具有映射关系“key-value对”的集合(couple) 3.Iterator接口&#…...
python ffmpeg合并ts文件
前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家:点击跳转 当你从网站下载了一集动漫,然后发现是一堆ts文件,虽然可以打开,但是某个都是10秒左右,…...

c++map和set剖析
文章参考文献:cplusplus 博主:拖拉机厂第一代码手 gitee:拖拉机厂第一代码手 c专栏:C 目录 🧙🏼♂set剖析🧚🏼set简介🧚🏼set模板参数列表🧚🏼s…...

kubernetes configmap 的data中的文件内容格式错乱
截取一段错乱的配置: kubectl -n monitoring get cm blackbox-exporter-configuration -o yaml apiVersion: v1 data:config.yml: "\"modules\":\n \"http_2xx\":\n \"http\":\n \"preferred_ip_protocol\"…...

A TupleBackedMap cannot be modified Mybatis分页,使用List<Map>接参,无法修改map的解决方案
问题描述 当使用Mybatis 进行Page分页,再使用Page< map >作为接受参数。此时尝试修改map则会报错。 报错为 java.lang.UnsupportedOperationException: A TupleBackedMap cannot be modified解决方案 使用新的数组,使用反射,构建工具…...

Leetcode-每日一题【剑指 Offer 13. 机器人的运动范围】
题目 地上有一个m行n列的方格,从坐标 [0,0] 到坐标 [m-1,n-1] 。一个机器人从坐标 [0, 0] 的格子开始移动,它每次可以向左、右、上、下移动一格(不能移动到方格外),也不能进入行坐标和列坐标的数位之和大于k的格子。例…...

WEB集群——负载均衡集群
目录 一、 LVS-DR 群集。 1、LVS-DR工作原理 2、LVS-DR模式的特点 3、部署LVS-DR集群 3.1 配置负载调度器(192.168.186.100) 3.2 第一台web节点服务器(192.168.186.103) 3.3 第二台web节点服务器(192.168.186.…...
ubuntu 20.0.4 搭建nvidia 显卡环境
一、安装docker 1、安装dokcer sudo apt install docker.io2、docker 添加到用户组 创建docker用户组 sudo groupadd docker添加当前用户加入docker用户组 sudo usermod -aG docker ${USER}重启docker服务 sudo systemctl restart docker切换或者退出当前账户再从新登入 …...
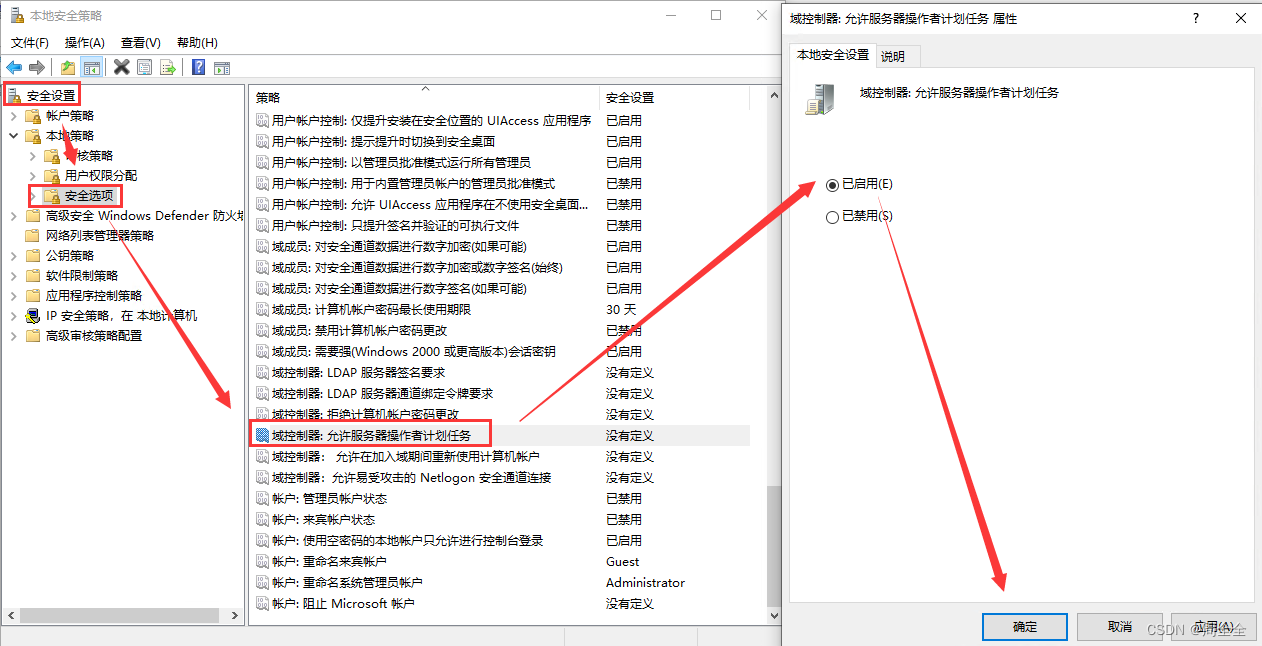
Windows环境下通过 系统定时 执行脚本方式 压缩并备份文件夹 到其他数据盘
环境配置 压缩时需要使用7-zip进行调用,因此根据自己电脑进行安装 官网:https://www.7-zip.org/ 脚本文件 新建记事本文件,重命名为git_back_up.bat echo off rem 设置utf-8可以正常显示中文 chcp 65001 > nulrem 获取当前日期和时间&…...

C++系列二:STL教程-常用算法
提示:写完文章后,目录可以自动生成,如何生成可参考右边的帮助文档 常用算法 前言算法列举:算法例子 前言 还有一些我在尝试中迷惑不解的,有点玄幻。 算法列举: 排序算法: sort(first, last);…...

【css】渐变
渐变是设置一种颜色或者多种颜色之间的过度变化。 两种渐变类型: 线性渐变(向下/向上/向左/向右/对角线) 径向渐变(由其中心定义) 1、线性渐变 语法:background-image: linear-gradient(direction, co…...
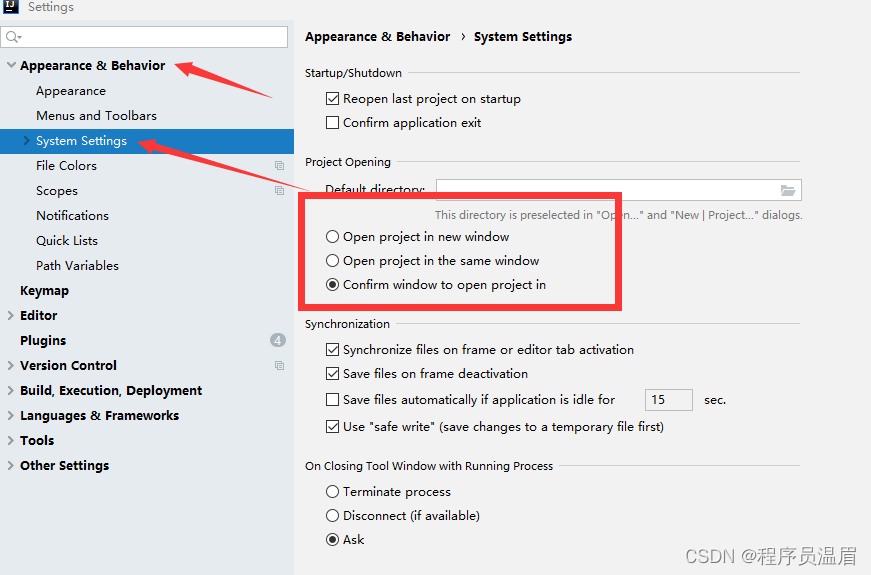
idea打开多个项目需要开多个窗口(恢复询问弹窗)
【版权所有,文章允许转载,但须以链接方式注明源地址,否则追究法律责任】【创作不易,点个赞就是对我最大的支持】 前言 仅作为学习笔记,供大家参考 总结的不错的话,记得点赞收藏关注哦! 使用…...

篇十三:策略模式:选择不同算法
篇十三:“策略模式:选择不同算法” 设计模式是软件开发中的重要知识,策略模式(Strategy Pattern)是一种行为型设计模式,用于在运行时根据不同的需求选择不同的算法或行为。本文将探讨策略模式的作用和实现…...

Centos7.6 安装mysql过程全记录
在centos 7.6上 离线安装mysql 的步骤,可参考下文: 一、查看当前MySQL的安装情况并卸载 1. 查看当前MySQL的安装情况 查找之前是否安装了MySQL rpm -qa|grep -i mysql 2.卸载mysql 如果已经安装mysql,则需要先停止MySQL,再删除…...

Java中的Guava是什么?
Java中的Guava是一个非常强大的Java库,它提供了很多实用的工具类和方法,可以帮助我们更高效地开发Java应用程序。从新手的角度来看,Guava可以让我们在Java编程中变得更加简单、快速和高效。 Guava的命名来源于“Google’s favorite Java lib…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

深入浅出WebGL:在浏览器中解锁3D世界的魔法钥匙
WebGL:在浏览器中解锁3D世界的魔法钥匙 引言:网页的边界正在消失 在数字化浪潮的推动下,网页早已不再是静态信息的展示窗口。如今,我们可以在浏览器中体验逼真的3D游戏、交互式数据可视化、虚拟实验室,甚至沉浸式的V…...

数据结构:泰勒展开式:霍纳法则(Horner‘s Rule)
目录 🔍 若用递归计算每一项,会发生什么? Horners Rule(霍纳法则) 第一步:我们从最原始的泰勒公式出发 第二步:从形式上重新观察展开式 🌟 第三步:引出霍纳法则&…...
