LeetCode解法汇总1749. 任意子数组和的绝对值的最大值
目录链接:
力扣编程题-解法汇总_分享+记录-CSDN博客
GitHub同步刷题项目:
https://github.com/September26/java-algorithms
原题链接:力扣
描述:
给你一个整数数组 nums 。一个子数组 [numsl, numsl+1, ..., numsr-1, numsr] 的 和的绝对值 为 abs(numsl + numsl+1 + ... + numsr-1 + numsr) 。
请你找出 nums 中 和的绝对值 最大的任意子数组(可能为空),并返回该 最大值 。
abs(x) 定义如下:
- 如果
x是负整数,那么abs(x) = -x。 - 如果
x是非负整数,那么abs(x) = x。
示例 1:
输入:nums = [1,-3,2,3,-4] 输出:5 解释:子数组 [2,3] 和的绝对值最大,为 abs(2+3) = abs(5) = 5 。
示例 2:
输入:nums = [2,-5,1,-4,3,-2] 输出:8 解释:子数组 [-5,1,-4] 和的绝对值最大,为 abs(-5+1-4) = abs(-8) = 8 。
提示:
1 <= nums.length <= 105-104 <= nums[i] <= 104
解题思路:
/**
* 1749. 任意子数组和的绝对值的最大值
* 1,-3,2,3,-4
* 2,-5,1,-4,3,-2
* 解题思路:
* 动态规划,构建2个数组dp1和dp2,dp1[i]代表数组右区间为i位,可能的最大的正数数组和,dp2[i]则为负数。
* 遍历的时候,如果nums[i+1] + dp1[i]>0,则dp1[i+1]=nums[i+1] + dp1[i],否则dp1[i+1]=0。dp2也是一样的逻辑。
* 找dp1和dp2最大的绝对值即可。
*/
代码:
class Solution1749
{
public:int maxAbsoluteSum(vector<int> &nums){vector<int> dp1(nums.size());vector<int> dp2(nums.size());if (nums[0] >= 0){dp1[0] = nums[0];dp2[0] = 0;}else{dp1[0] = 0;dp2[0] = nums[0];}int absValue = max(abs(dp1[0]), abs(dp2[0]));for (int i = 1; i < nums.size(); i++){int value = nums[i];if (value >= 0){dp1[i] = value + dp1[i - 1];dp2[i] = min(value + dp2[i - 1], 0);}else{dp1[i] = max(value + dp1[i - 1], 0);dp2[i] = value + dp2[i - 1];}absValue = max(absValue, max(abs(dp1[i]), abs(dp2[i])));}return absValue;}
};相关文章:

LeetCode解法汇总1749. 任意子数组和的绝对值的最大值
目录链接: 力扣编程题-解法汇总_分享记录-CSDN博客 GitHub同步刷题项目: https://github.com/September26/java-algorithms 原题链接:力扣 描述: 给你一个整数数组 nums 。一个子数组 [numsl, numsl1, ..., numsr-1, numsr] 的…...
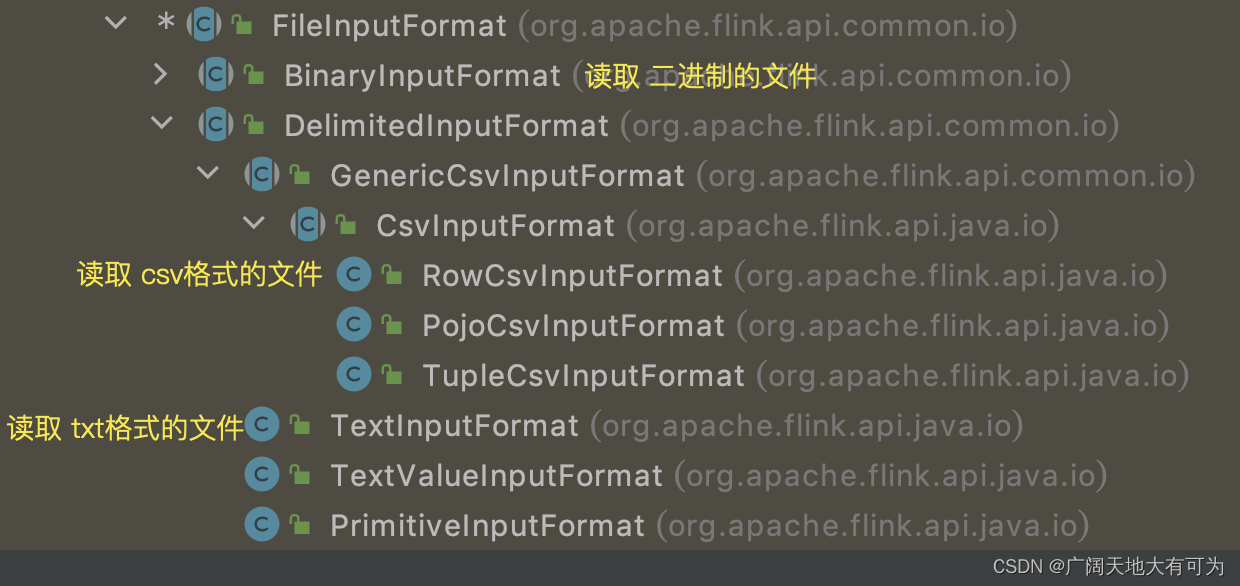
4.2、Flink任务怎样读取文件中的数据
目录 1、前言 2、readTextFile(已过时,不推荐使用) 3、readFile(已过时,不推荐使用) 4、fromSource(FileSource) 推荐使用 1、前言 思考: 读取文件时可以设置哪些规则呢? 1. 文件的格式(tx…...

Effective Java笔记(28)列表优于数组
数组与泛型相比,有两个重要的不同点 。 首先,数组是协变的( covariant ) 。 这个词听起来有点吓人,其实只是表示如果 Sub 为 Super 的子类型,那么数组类型 Sub[ ]就是Super[ ]的子类型。 相反,泛…...

做BI领域的ChatGPT,思迈特升级一站式ABI平台
8月8日,以「指标驱动 智能决策」为主题,2023 Smartbi V11系列新品发布会在广州丽思卡尔顿酒店开幕。 后疫情时代,BI发展趋势的观察与应对 在发布会上,思迈特CEO吴华夫在开场致辞中表示,当前大环境背景下…...
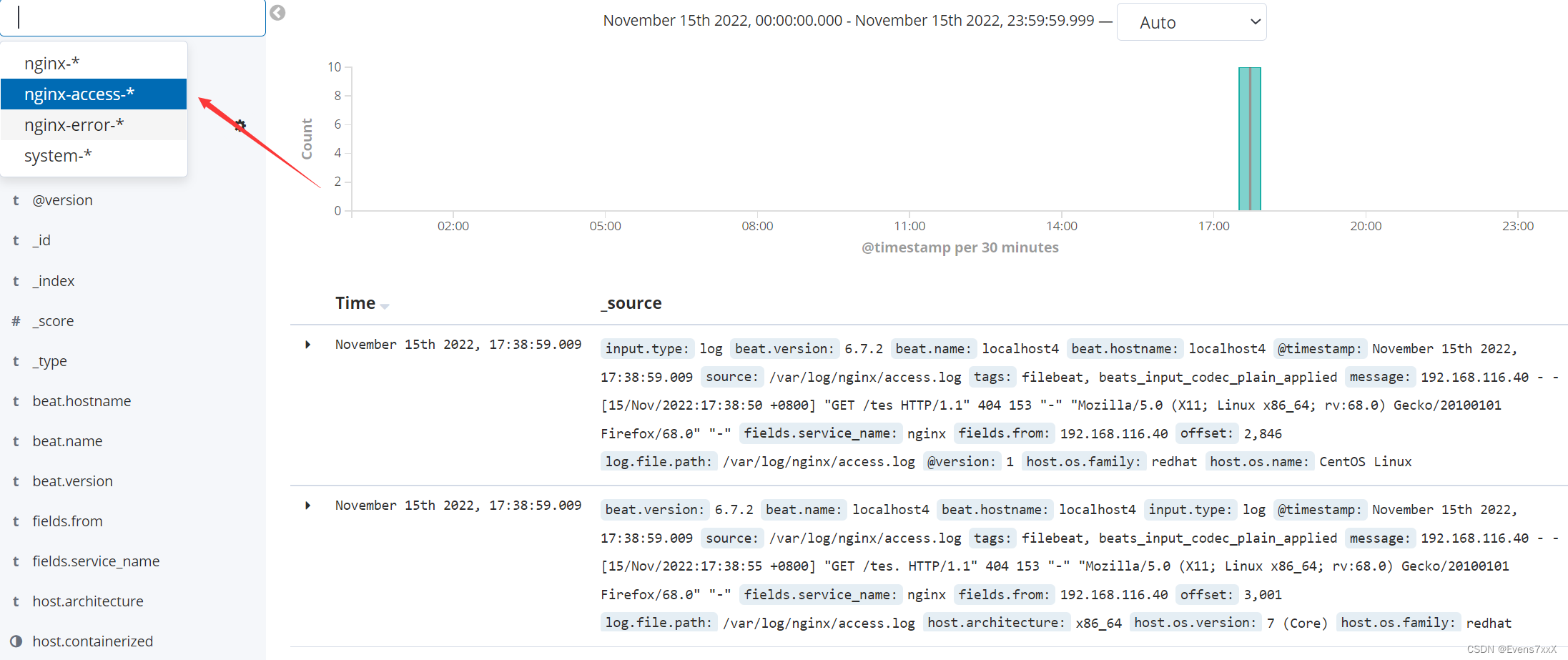
ELFK——ELK结合filebeat日志分析系统(2)
目录 一、filebeat 二、ELFK 1.原理简介 2.在ELK基础上部署filebeat 一、filebeat Filebeat,轻量级的开源日志文件数据搜集器。通常在需要采集数据的客户端安装 Filebeat,并指定目录与日志格式,Filebeat 就能快速收集数据,并…...

webSocket 协议是什么
webSocket 协议是什么,能简述一下吗? websocket 协议 HTML5 带来的新协议,相对于 http,它是一个持久连接的协议,它利用 http 协议完成握手,然后通过 TCP 连接通道发送消息,使用 websocket 协议可…...

CentOS 7迁移Anolis OS 8
背景:生产环境客户要求操作系统国产化 操作系统:Centos7.9 内核:5.4.108 服务器可以联网,进行在线迁移: # 下载迁移工具软件源 wget https://mirrors.openanolis.cn/anolis/migration/anolis-migration.repo -O /etc/y…...

Transformer 立体视觉 Depth Estimation
1. Intro 立体深度估计具有重要的意义,因为它能够重建三维信息。为此,在左右相机图像之间匹配相应的像素;对应像素位置的差异,即视差,可以用来推断深度并重建3D场景。最近基于深度学习的立体深度估计方法已经显示出有希望的结果,但仍然存在一些挑战。 其中一个挑战涉及使…...
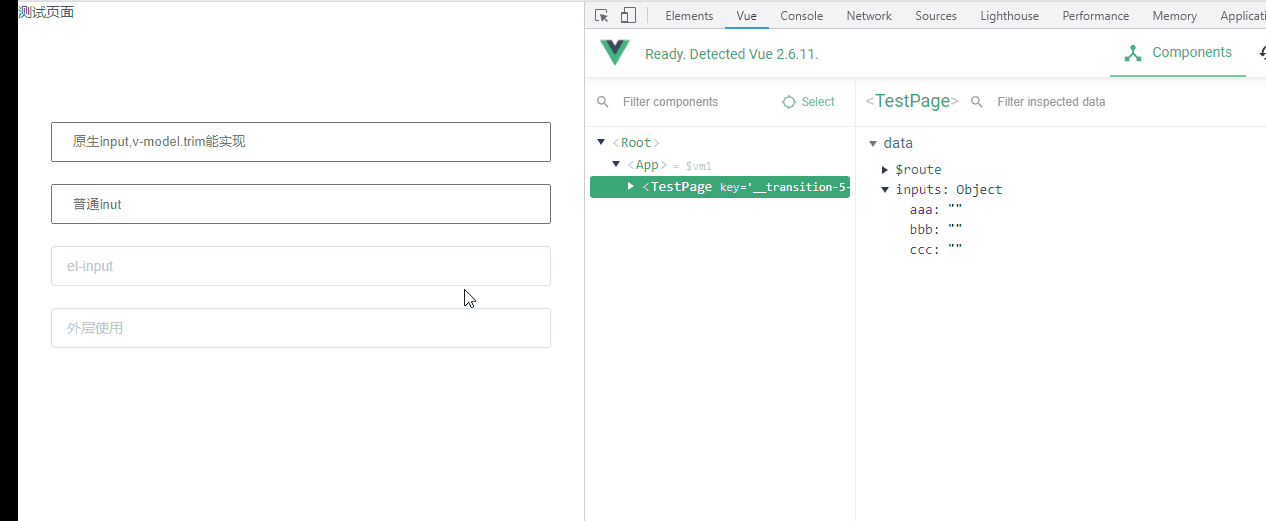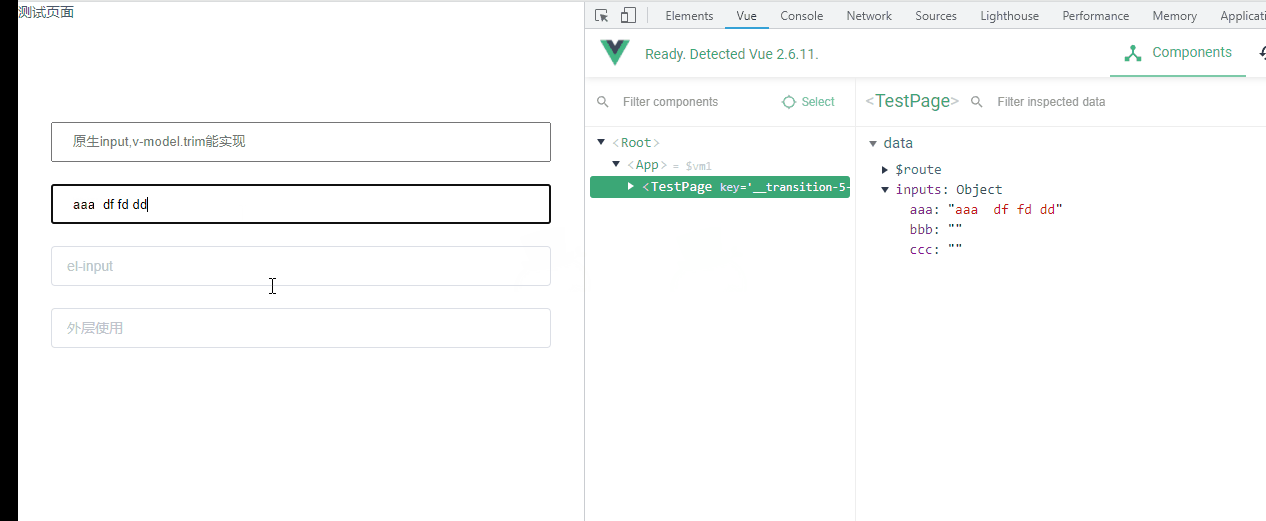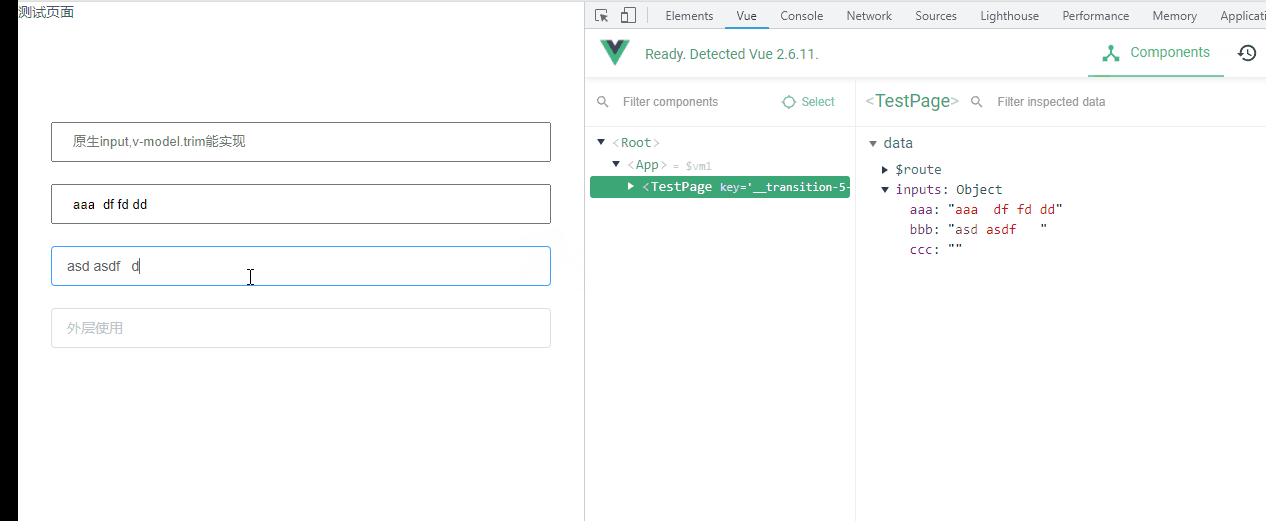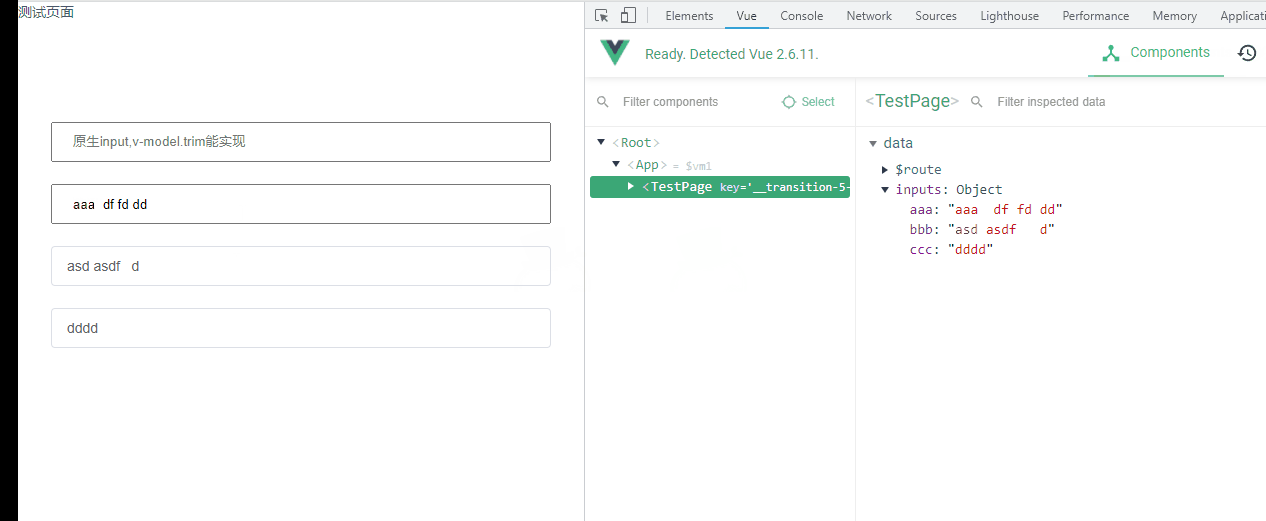
vue去掉所有输入框两边空格,封装指令去空格,支持Vue2和Vue3,ElementUI Input去空格
需求背景 就是页面很多表单输入框,期望在提交的时候,都要把用户两边的空格去掉 ❌使用 vue 的指令 .trim 去掉空格 中间会输入不了空格, 比如我想输入 你好啊 中国, 这中间的空格输入不了,只能变成 你好啊中国 ❌在提交的时候使用…...
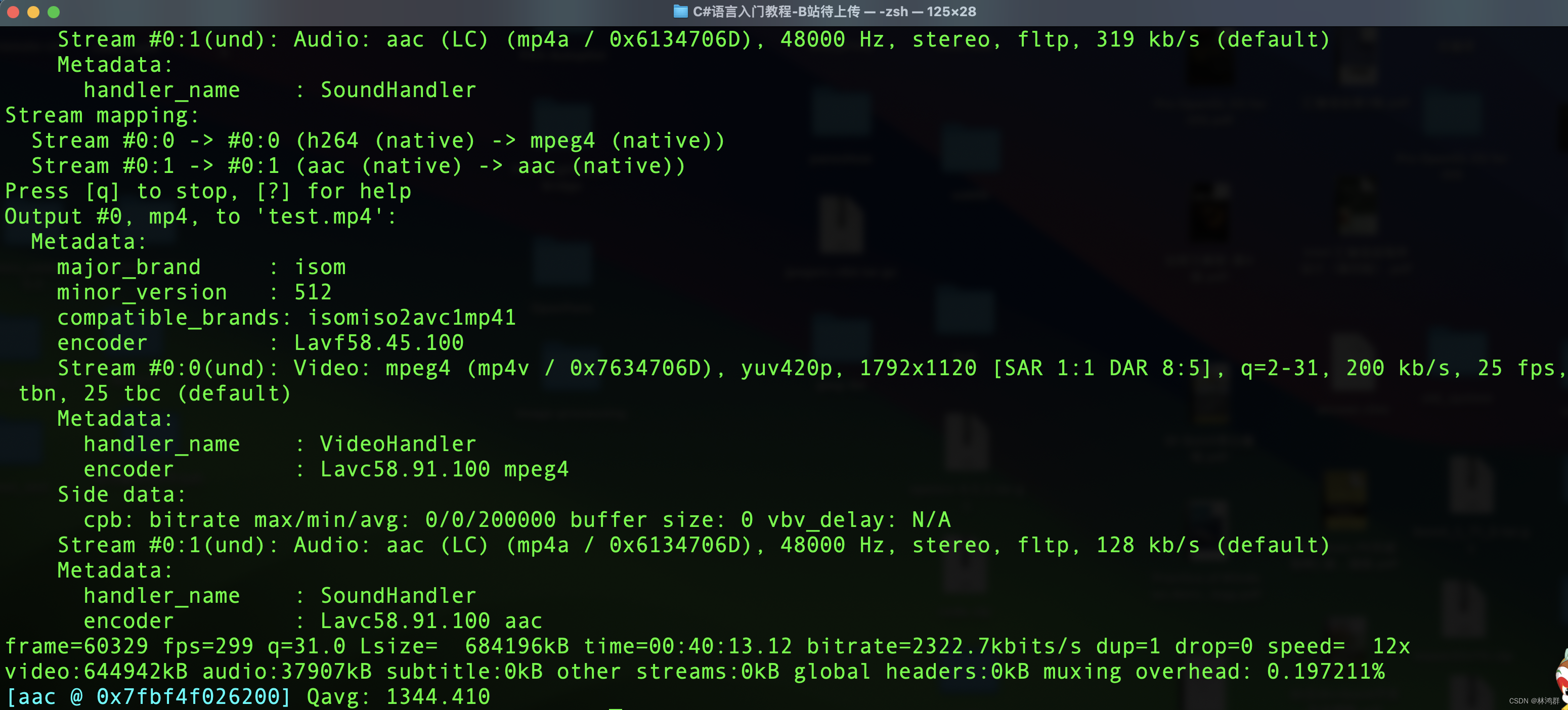
认识FFMPEG框架
FFMPEG全称: Fast Forward Moving Picture Experts Group (MPEG:动态图像专家组) ffmpeg相关网站: git://source.ffmpeg.org/ffmpeg.git http://git.videolan.org/?pffmpeg.git https://github.com/FFmpeg/FFmpeg FFMPEG框架基本组件: AVFormat , AVCodec, AVDevice, AVFil…...

Vue3 大屏数字滚动效果
父组件: <template> <div class"homePage"> <NumRoll v-for"(v, i) in numberList" :key"i" :number"v"></NumRoll> </div> </template> <script setup> import { onMounted, r…...
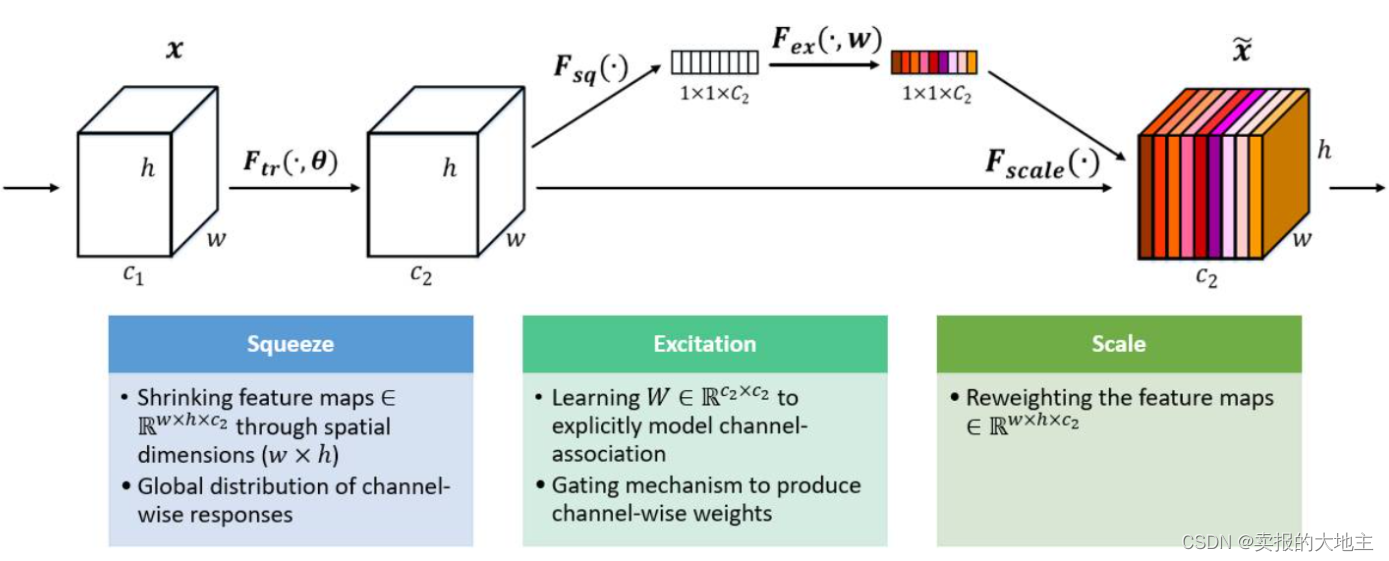
【深度学习注意力机制系列】—— SENet注意力机制(附pytorch实现)
深度学习中的注意力机制(Attention Mechanism)是一种模仿人类视觉和认知系统的方法,它允许神经网络在处理输入数据时集中注意力于相关的部分。通过引入注意力机制,神经网络能够自动地学习并选择性地关注输入中的重要信息ÿ…...

go 函数
go 语言函数 go 函数函数定义Go函数的特点如下函数作为参数可变参数相同类型可变参数不同类型可变参数 return语句作用概述空的return语句空白标识符多个返回值命名返回值 defer 语句作用引申出来的面试题for defer下面是一个使用defer的示例代码输出结果 匿名函数定义匿名函数…...

python之正则表达式
目录 正则表达式 python正则表达式方法 match search findall finditer compile 元字符匹配 元字符 量词 贪婪匹配和惰性匹配 正则表达式的group 语法 案例 正则表达式 正则表达式又称规则表达式,是使用单个字符串来描述、匹配某个句法规则的字符串…...
【LeetCode每日一题】——219.存在重复元素II
文章目录 一【题目类别】二【题目难度】三【题目编号】四【题目描述】五【题目示例】六【题目提示】七【解题思路】八【时间频度】九【代码实现】十【提交结果】 一【题目类别】 哈希表 二【题目难度】 简单 三【题目编号】 219.存在重复元素II 四【题目描述】 给你一个…...

篇六:适配器模式:让不兼容变兼容
篇六:“适配器模式:让不兼容变兼容” 开始本篇文章之前先推荐一个好用的学习工具,AIRIght,借助于AI助手工具,学习事半功倍。欢迎访问:http://airight.fun/ 另外有2本不错的关于设计模式的资料,…...

【云原生】Docker-compose中所有模块学习
compose模块 模板文件是使用 Compose 的核心,涉及到的指令关键字也比较多。但大家不用担心,这里面大部分指令跟 docker run 相关参数的含义都是类似的。 默认的模板文件名称为 docker-compose.yml,格式为 YAML 格式。 version: "3&quo…...

广义积分练习
前置知识 无穷限积分瑕积分 练习 计算 ∫ 0 ∞ 1 x ( 1 x ) d x \int_0^{\infty}\dfrac{1}{\sqrt x(1x)}dx ∫0∞x (1x)1dx 解: x 0 \qquad x0 x0为瑕点 \qquad 原式 lim a → 0 lim b → ∞ ∫ a b 1 x ( 1 x ) d x lim a → 0 lim …...
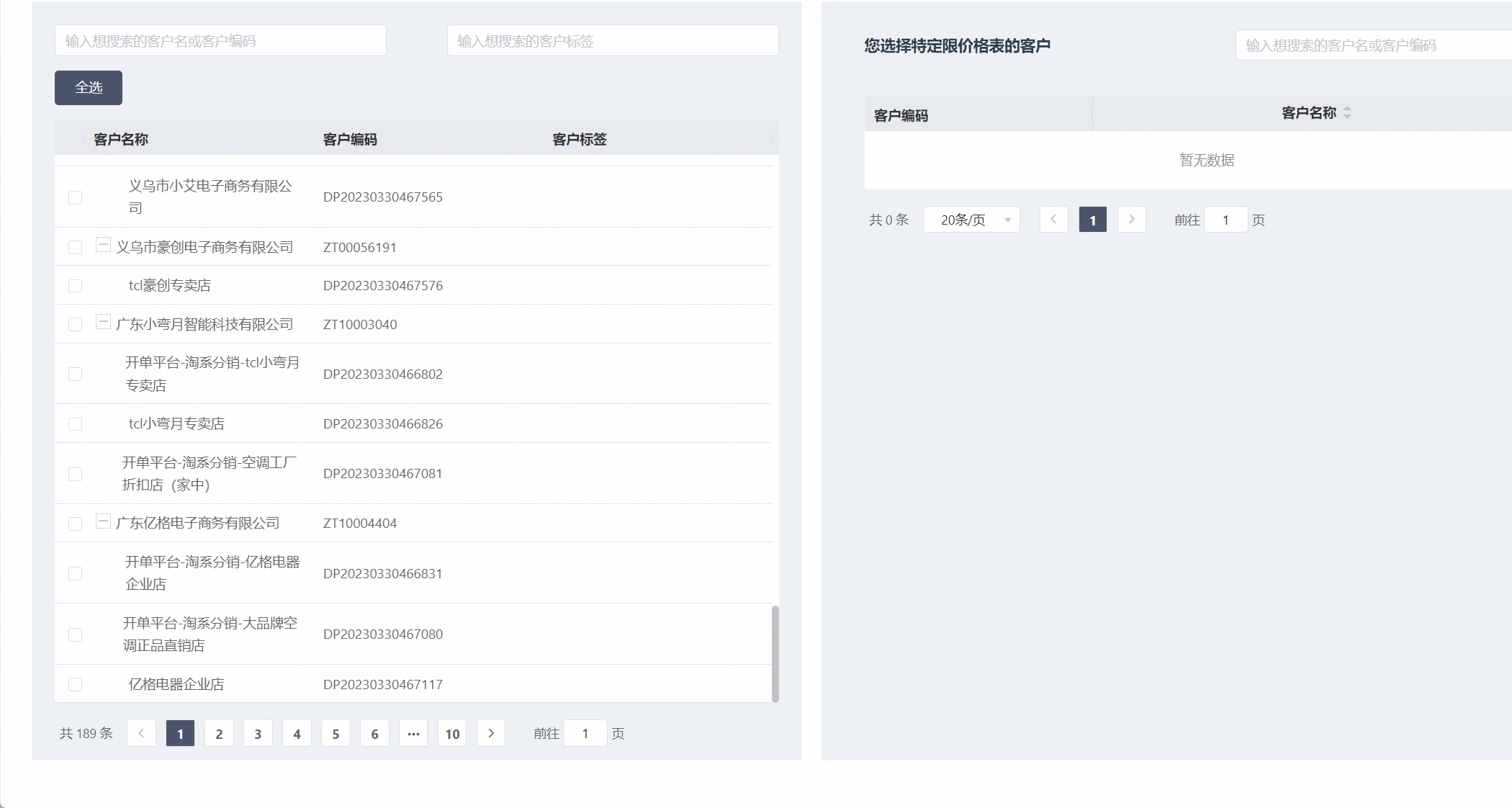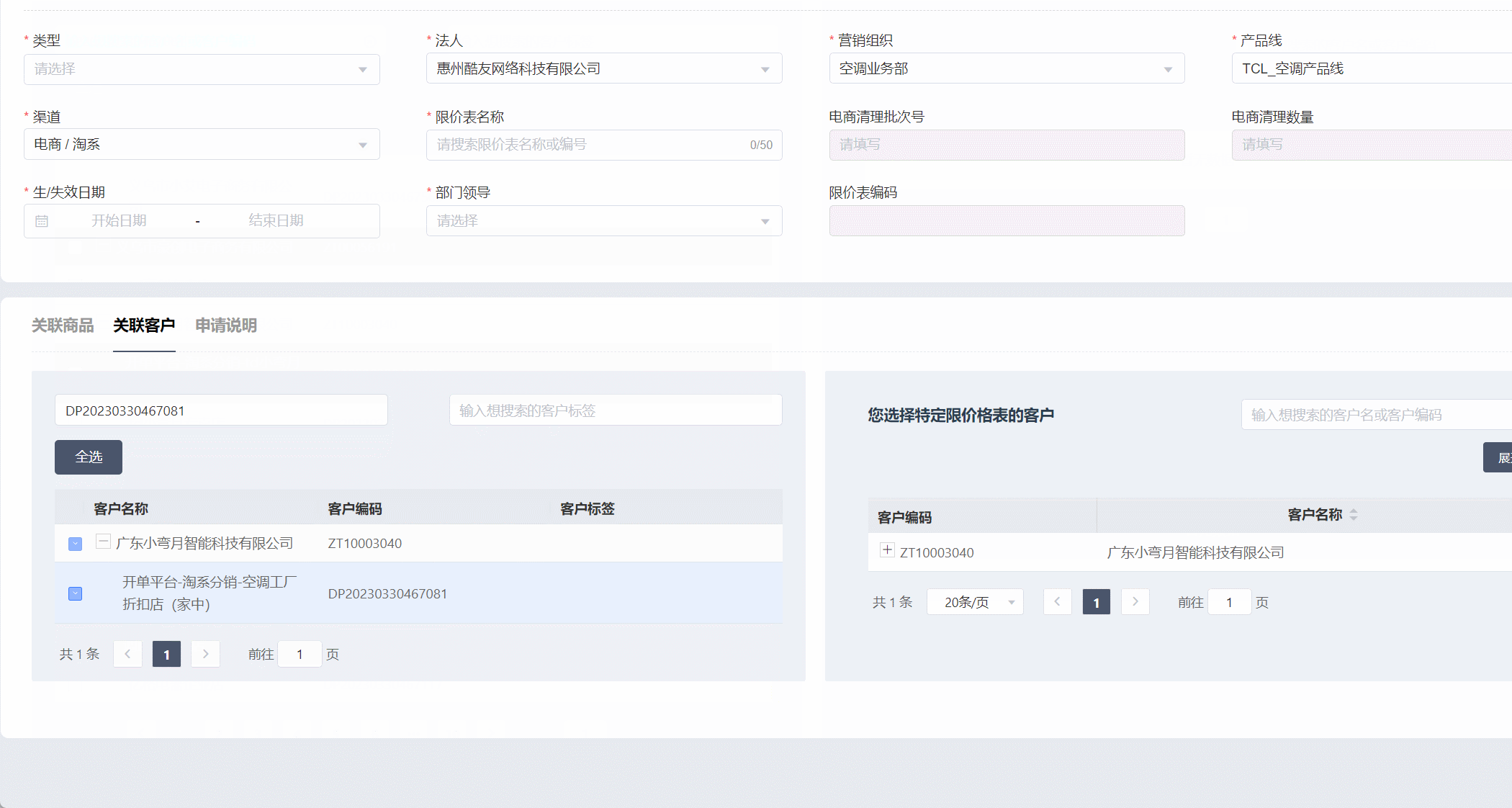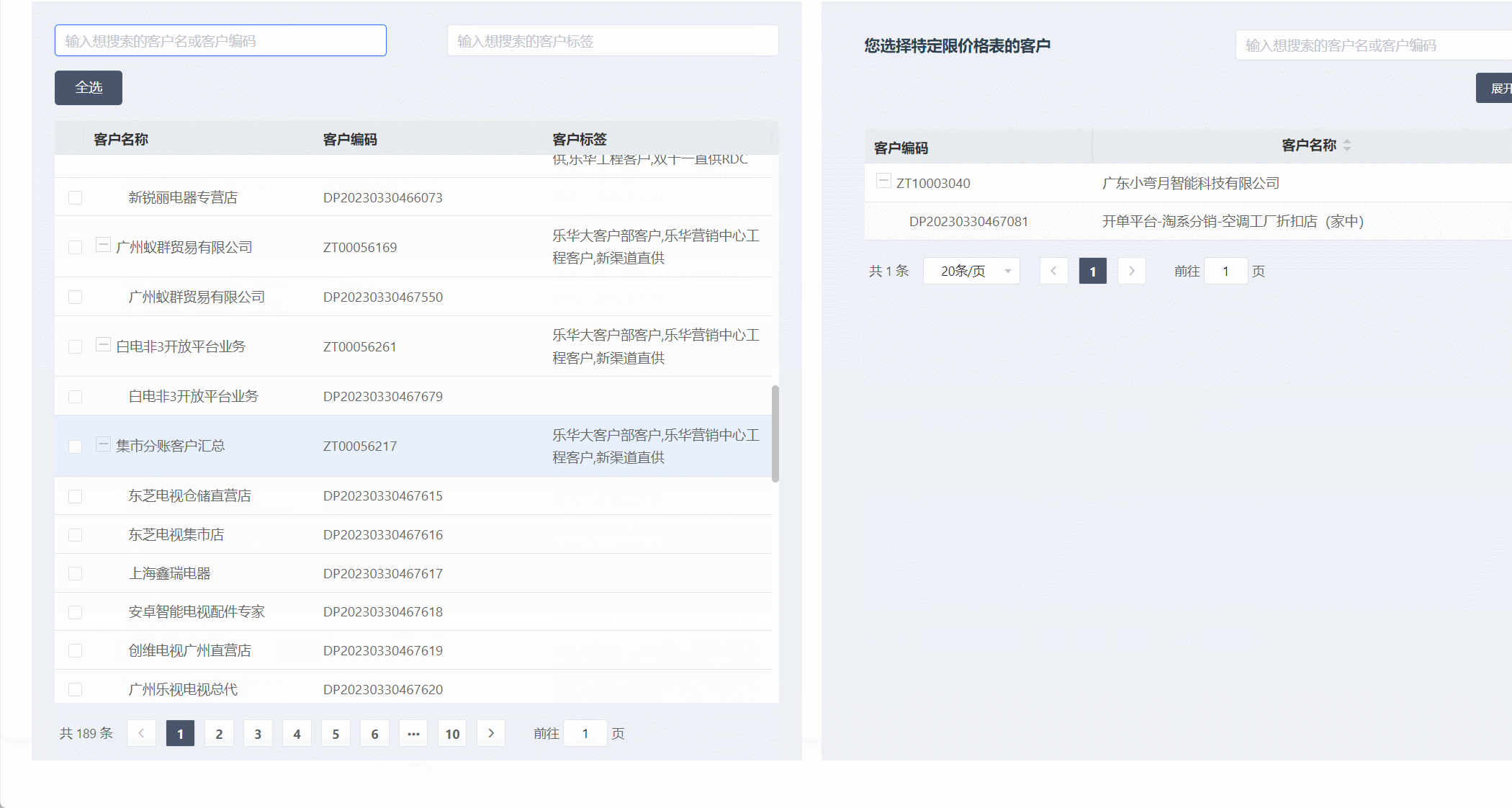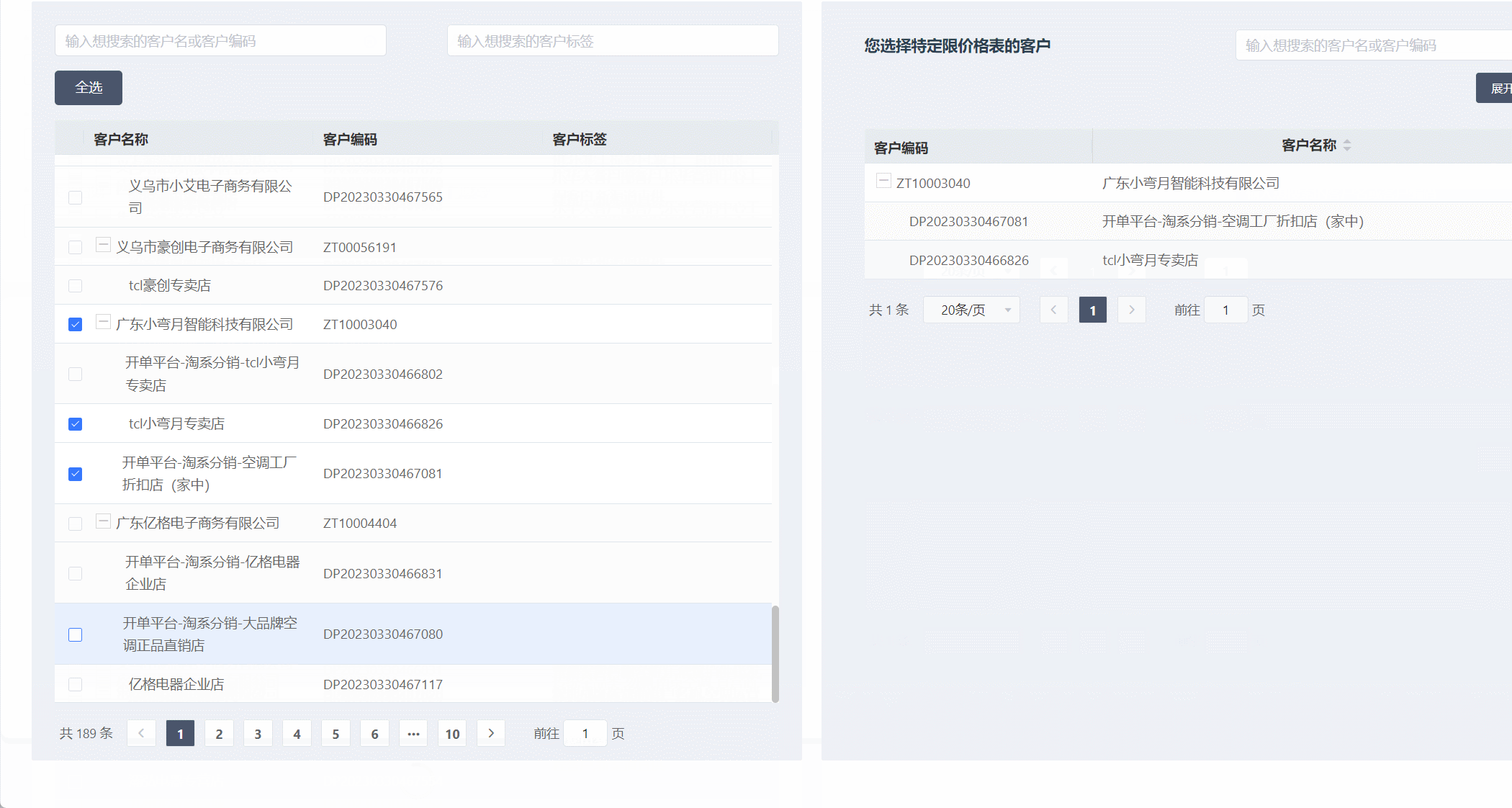
element-ui树形表格,左边勾选,右边显示选中的数据-功能(如动图)
功能如图 功能需求 表格树形表格勾选数据,右边显示对应勾选的数据内容,选中客户,自动勾选所有的店铺(子级),选中其中一个店铺,自动勾选上客户(父级),同时会存在只有客户(下面没有子级的情况&am…...

Android数字价格变化的动画效果的简单实现
原理:使用ValueAnimator属性动画类实现,它通过值的改变手动设置对象的属性值来实现动画效果。直接贴代码: public static void doNumberAnim(TextView tvPrice, float startNumber, float endNumber) {ValueAnimator animator ValueAnimato…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

掌握 HTTP 请求:理解 cURL GET 语法
cURL 是一个强大的命令行工具,用于发送 HTTP 请求和与 Web 服务器交互。在 Web 开发和测试中,cURL 经常用于发送 GET 请求来获取服务器资源。本文将详细介绍 cURL GET 请求的语法和使用方法。 一、cURL 基本概念 cURL 是 "Client URL" 的缩写…...
