算法刷题打卡第94天: 找出给定方程的正整数解
找出给定方程的正整数解
难度:中等
给你一个函数 f(x, y) 和一个目标结果 z,函数公式未知,请你计算方程 f(x,y) == z 所有可能的正整数 数对 x 和 y。满足条件的结果数对可以按任意顺序返回。
尽管函数的具体式子未知,但它是单调递增函数,也就是说:
f(x, y) < f(x + 1, y)f(x, y) < f(x, y + 1)
函数接口定义如下:
interface CustomFunction {
public:// Returns some positive integer f(x, y) for two positive integers x and y based on a formula.int f(int x, int y);
};
你的解决方案将按如下规则进行评判:
- 判题程序有一个由
CustomFunction的9种实现组成的列表,以及一种为特定的z生成所有有效数对的答案的方法。 - 判题程序接受两个输入:
function_id(决定使用哪种实现测试你的代码)以及目标结果z。 - 判题程序将会调用你实现的
findSolution并将你的结果与答案进行比较。 - 如果你的结果与答案相符,那么解决方案将被视作正确答案,即
Accepted。
示例 1:
输入:function_id = 1, z = 5
输出:[[1,4],[2,3],[3,2],[4,1]]
解释:function_id = 1 暗含的函数式子为 f(x, y) = x + y
以下 x 和 y 满足 f(x, y) 等于 5:
x=1, y=4 -> f(1, 4) = 1 + 4 = 5
x=2, y=3 -> f(2, 3) = 2 + 3 = 5
x=3, y=2 -> f(3, 2) = 3 + 2 = 5
x=4, y=1 -> f(4, 1) = 4 + 1 = 5
示例 2:
输入:function_id = 2, z = 5
输出:[[1,5],[5,1]]
解释:function_id = 2 暗含的函数式子为 f(x, y) = x * y
以下 x 和 y 满足 f(x, y) 等于 5:
x=1, y=5 -> f(1, 5) = 1 * 5 = 5
x=5, y=1 -> f(5, 1) = 5 * 1 = 5
二分查找
思路:
- 先用二分查找x的最小值和最大值
- 再在x的这个区间中,二分查找y值
复杂度分析:
- 时间复杂度: O(mlogn)O(m \log n)O(mlogn),其中 mmm 是 xxx 的取值数目,nnn 是 yyy 的取值数目。
- 空间复杂度: O(1)O(1)O(1)。返回值不计入空间复杂度。
"""This is the custom function interface.You should not implement it, or speculate about its implementationclass CustomFunction:# Returns f(x, y) for any given positive integers x and y.# Note that f(x, y) is increasing with respect to both x and y.# i.e. f(x, y) < f(x + 1, y), f(x, y) < f(x, y + 1)def f(self, x, y):"""class Solution:def findSolution(self, customfunction: 'CustomFunction', z: int) -> List[List[int]]:# 求 x 可能的最大值l1, r1 = 1, 1000while l1 <= r1: mid = (l1 + r1) // 2 if customfunction.f(mid, 1) > z:r1 = mid - 1else:l1 = mid + 1# 求 x 可能的最小值 l2, r2 = 1, l1while l2 <= r2: mid = (l2 + r2) // 2 if customfunction.f(mid, 1000) < z:l2 = mid + 1else:r2 = mid - 1# 求 x 合理区间内,和 y 可能的数组res = []for i in range(l2, l1):l, r = 1, 1000while l <= r:mid = (l + r) // 2if customfunction.f(i, mid) == z:res.append([i, mid])breakelif customfunction.f(i, mid) > z:r = mid - 1else:l = mid + 1return res
双指针
思路:
假设 x1<x2x_1 < x_2x1<x2,且 f(x1,y1)=f(x2,y2)=zf(x_1, y_1) = f(x_2, y_2) = zf(x1,y1)=f(x2,y2)=z,显然有 y1>y2y_1 > y_2y1>y2。因此我们从小到大进行枚举 xxx,并且从大到小枚举 yyy,当固定 xxx 时,不需要重头开始枚举所有的 yyy,只需要从上次结束的值开始枚举即可。
有个思路是用二分查找缩小x的范围,理论上应该更快。
复杂度分析:
- 时间复杂度: O(m+n)O(m+n)O(m+n),其中 mmm 是 xxx 的取值数目,nnn 是 yyy 的取值数目。
- 空间复杂度: O(1)O(1)O(1)。返回值不计入空间复杂度。
"""This is the custom function interface.You should not implement it, or speculate about its implementationclass CustomFunction:# Returns f(x, y) for any given positive integers x and y.# Note that f(x, y) is increasing with respect to both x and y.# i.e. f(x, y) < f(x + 1, y), f(x, y) < f(x, y + 1)def f(self, x, y):"""class Solution:def findSolution(self, customfunction: 'CustomFunction', z: int) -> List[List[int]]:y = 1000res = []for x in range(1, 1001):while y and customfunction.f(x, y) > z:y -= 1if y == 0:breakif customfunction.f(x, y) == z:res.append([x, y])return res
源:力扣(LeetCode)
链接:https://leetcode.cn/problems/find-positive-integer-solution-for-a-given-equation
相关文章:

算法刷题打卡第94天: 找出给定方程的正整数解
找出给定方程的正整数解 难度:中等 给你一个函数 f(x, y) 和一个目标结果 z,函数公式未知,请你计算方程 f(x,y) z 所有可能的正整数 数对 x 和 y。满足条件的结果数对可以按任意顺序返回。 尽管函数的具体式子未知,但它是单调…...
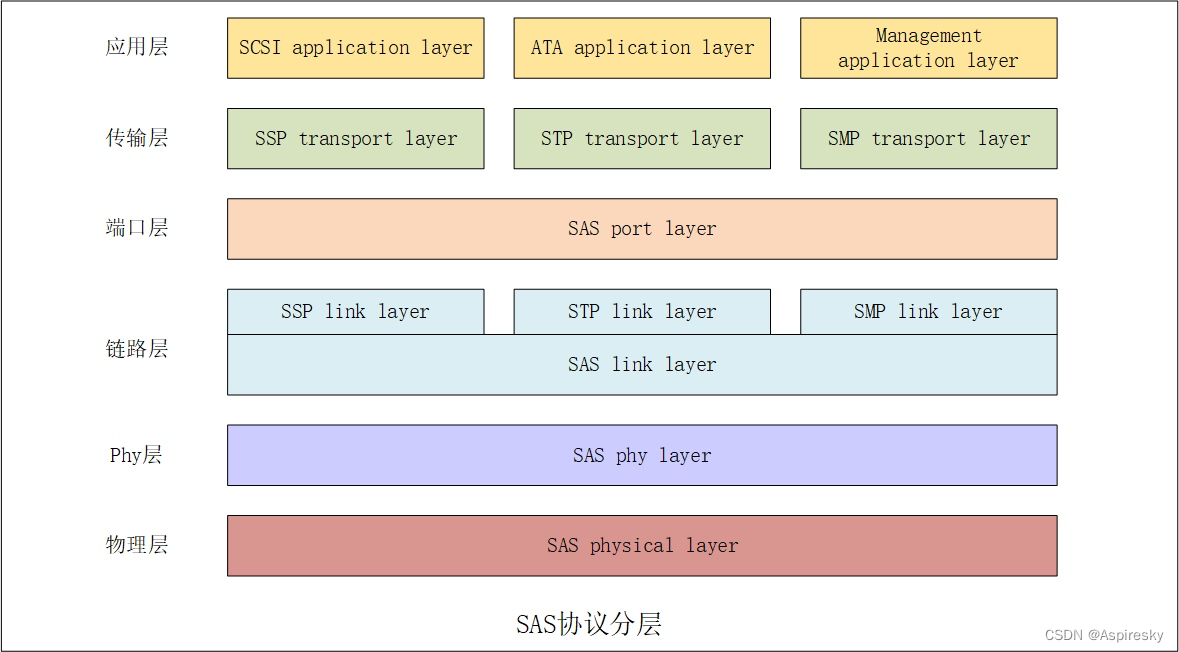
浅析SAS协议(1):基本介绍
文章目录概述SAS协议发展历程SAS技术特性SAS设备拓扑SAS phySAS地址SAS设备类型SAS协议分层参考链接概述 SAS,全称Serial Attached SCSI,即串行连结SCSI,是一种采用了串行总线的高速互连技术。通过物理上使用串行总线连结,在链路…...
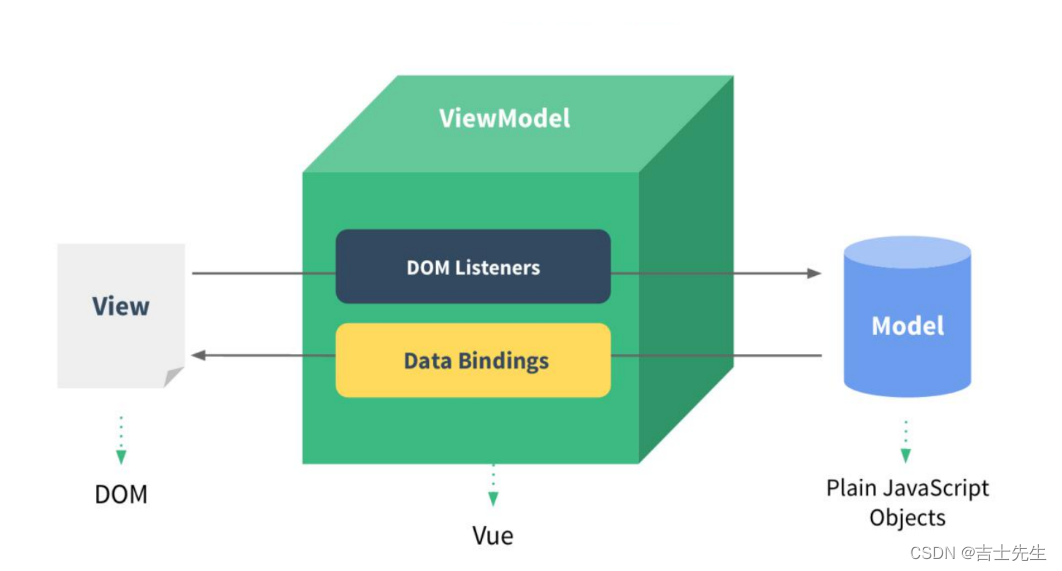
93.【Vue-细刷-02】
Vue-02(十六)、基本列表渲染 (v-for)1.使用v-for遍历数组2.使用v-for遍历对象3.使用v-for遍历字符串(十七)、列表过滤 (filter())1.⭐JS中Change属性的原生状态⭐2.使用watch监听实现3.const {xxx} this 在Vue的作用⭐⭐4.JS箭头函数参数的简写⭐5.使用computed进行计算实现(最…...
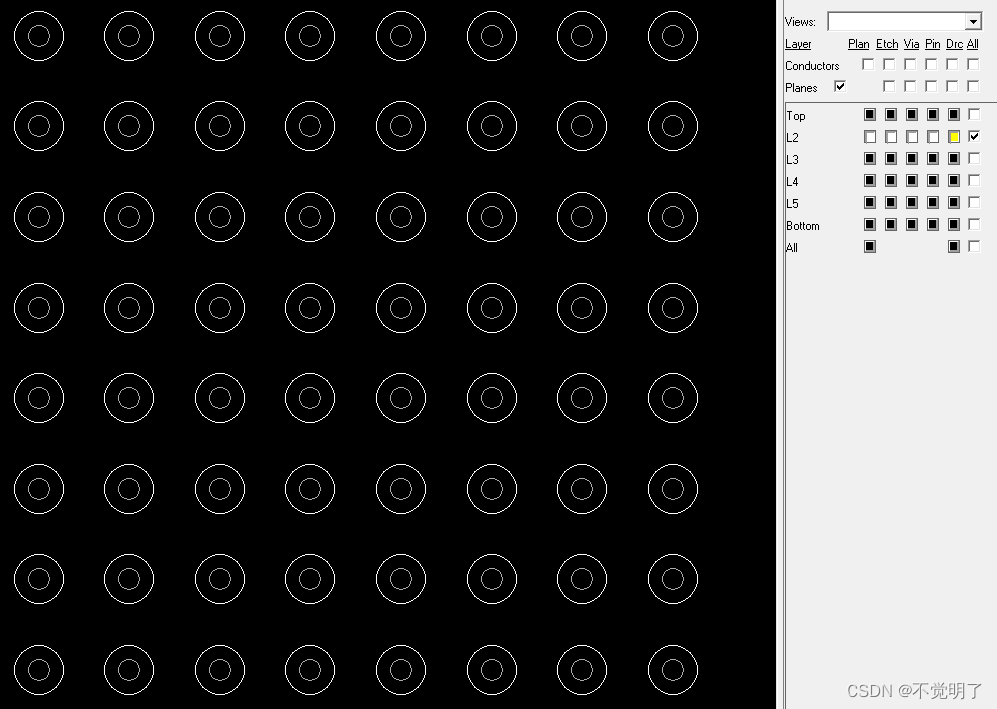
Allegro负片层不显示反盘的原因和解决办法
Allegro负片层不显示反盘的原因和解决办法 在用Allegro做PCB设计的时候,负片设计是较为常用的一种方式,有时会出现打开负片层却看不到反盘的情况,如下图 L2层是负片层 L2层仍然只能看到盘 如何才能看到反盘显示的效果,具体操作如下 首先确定L2层层叠里面设置的是负片...
ACM数论 裴蜀定理(贝祖定理)
一.内容定义 「裴蜀定理」,又称贝祖定理(Bzouts lemma)。是一个关于最大公约数的定理。其内容定义为:对于不全为零的任意整数 a 和 b,记二者的最大公约数为 g 即 gcd(a,b) g,则对于任意整数 x 和 y 都一定…...
解析)
基础篇—CSS Position(定位)解析
CSS Position(定位) position 属性指定了元素的定位类型。 position 属性的五个值: relativefixedabsolutesticky元素可以使用的顶部,底部,左侧和右侧属性定位。然而,这些属性无法工作,除非是先设定position属性。他们也有不同的工作方式,这取决于定位方法。 1、static…...

正则表达式与grep
基本正则表达式BRE集合 匹配字符匹配次数位置锚定 符号作用^尖角号,用于模式的最正常,如“^haha”,匹配以haha单词开头的行$美元符,用于模式的最右侧,如“haha$”,表示haha单词结尾的行^$组合符ÿ…...
开发必备的IDEA 插件!效率提升 50 倍!
日常开发中,面向百度编程的程序员,很多时候,你跟大佬级别的差距,可能不仅仅是知识面的差距,还有就是开发效率的差距。以下是我常用的几个IDEA插件,废话不多说,直接肝干货! 1. Codot…...

aws eks 集群访问ecr仓库拉取镜像的认证逻辑
本文主要讨论三个问题 ecr帮助程序在docker上如何配置eks集群访问ecr仓库的逻辑kubelet授权ecr的源码分析 ecr帮助程序 在docker环境下,可以通过在$HOME/.docker/config.json中指定凭证管理程序 docker login aws同样提供了证书助手,避免手动执行ecr认…...
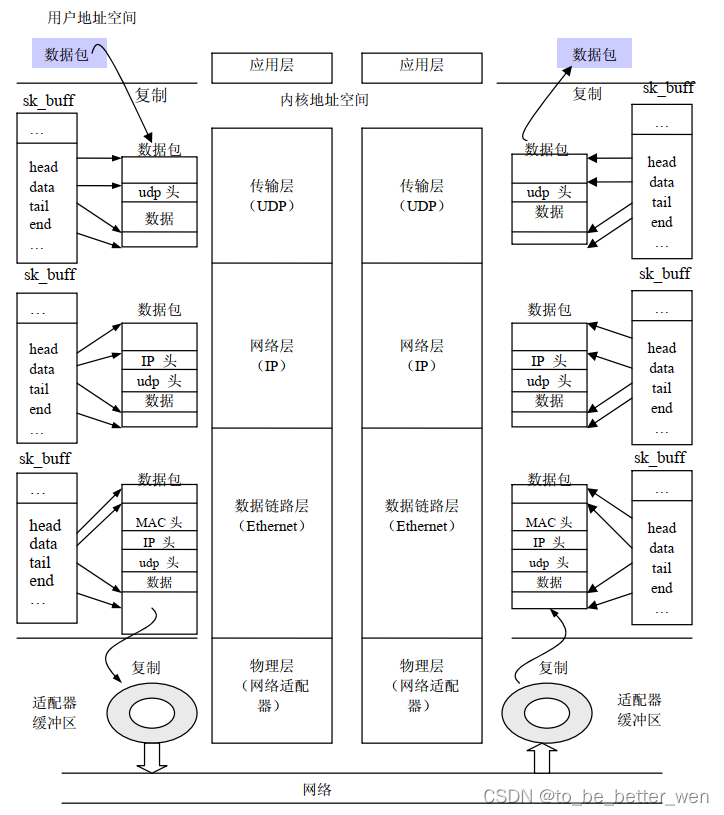
Linux Socket Buffer介绍
一. 前言 Linux内核网络子系统的实现之所以灵活高效,主要是在于管理网络数据包的缓冲器-socket buffer设计得高效合理。在Linux网络子系统中,socket buffer是一个关键的数据结构,它代表一个数据包在内核中处理的整个生命周期。 二. Socket Bu…...
ACL与NAT
ACL---访问控制列表,是一种策略控制工具 功能:1.定义感兴趣流量(数据层面 ) 2.定义感兴趣路由(控制层面) ACL 条目表项组成: 编号规则:步数或者跳数默认值为5,…...

使用gdb来debug程序并查找Segmentation fault原因
GDB 调试前言GDB基础用法1.启动及退出调试2.设置参数3.执行程序4.流程控制5.设置断点6.输出信息7.查看栈帧8.info命令9.显示源码GDB调试coredump文件关注公众号【程序员DeRozan】,回复【1207】,免费获取计算机经典资料及现金红包 前言 在开发程序时&…...

vbs简单语法及简单案例
文章目录一、简单语法1、变量2、输入3、输出4、选择语句5、循环二、用记事本编译中文乱码问题三、制作一个简单vbs脚本表白一、简单语法 1、变量 语法: dim 变量名例: dim a,b a1 b2 msgbox ab运行: 2、输入 语法:InputBox(…...

学板绘课程学费一般多少钱
学板绘课程学费一般多少钱?培训机构的费用和师资、模式有关,价格贵不贵要结合相同类型的机构多多对比。因为好些平台做了很多的宣传广告,运营成本很高, 终羊毛出在羊身上,这样的机构知名度很高,但是性价比不…...
- 实现一个可以用的模板)
48.在ROS中实现local planner(1)- 实现一个可以用的模板
有了之前45.在ROS中实现global planner(1)- 实现一个可以用模板的global planner的经验, 现在再去创建一个local planner的包就容易多了 1. 创建包 创建 cd ~/pibot_ros/ros_ws/src # 这里可以使用自己的ros workspace catkin_create_pkg sample_loc…...
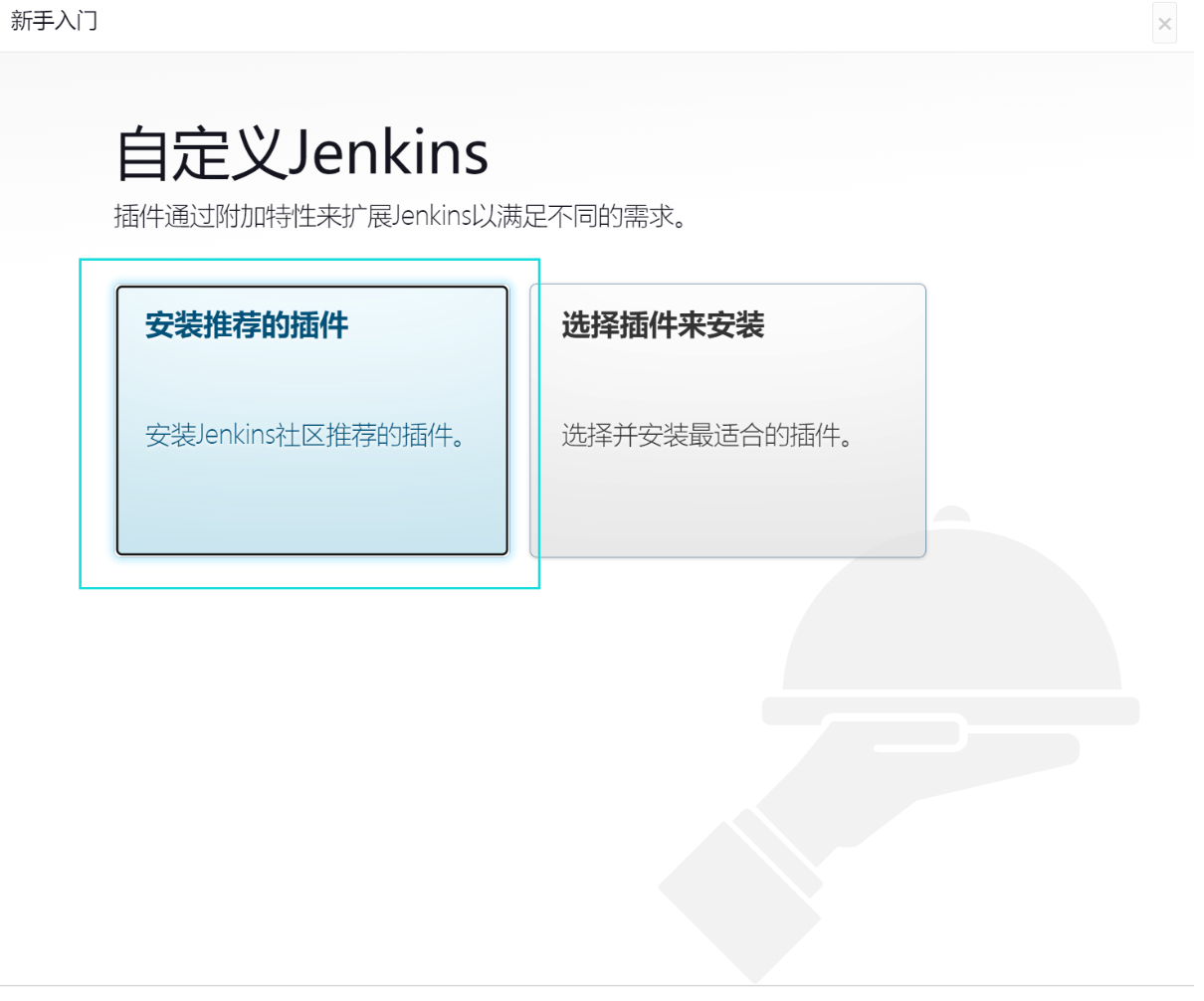
jenkins基础部署
一、jenkins是什么1.Jenkins的前身是Hudson,采用JAVA编写的持续集成开源工具。Hudson由Sun公司在2004年启动,第一个版本于2005年在java.net发布。2007年开始Hudson逐渐取代CruiseControl和其他的开源构建工具的江湖地位。在2008年的JavaOne大会上在开发者…...
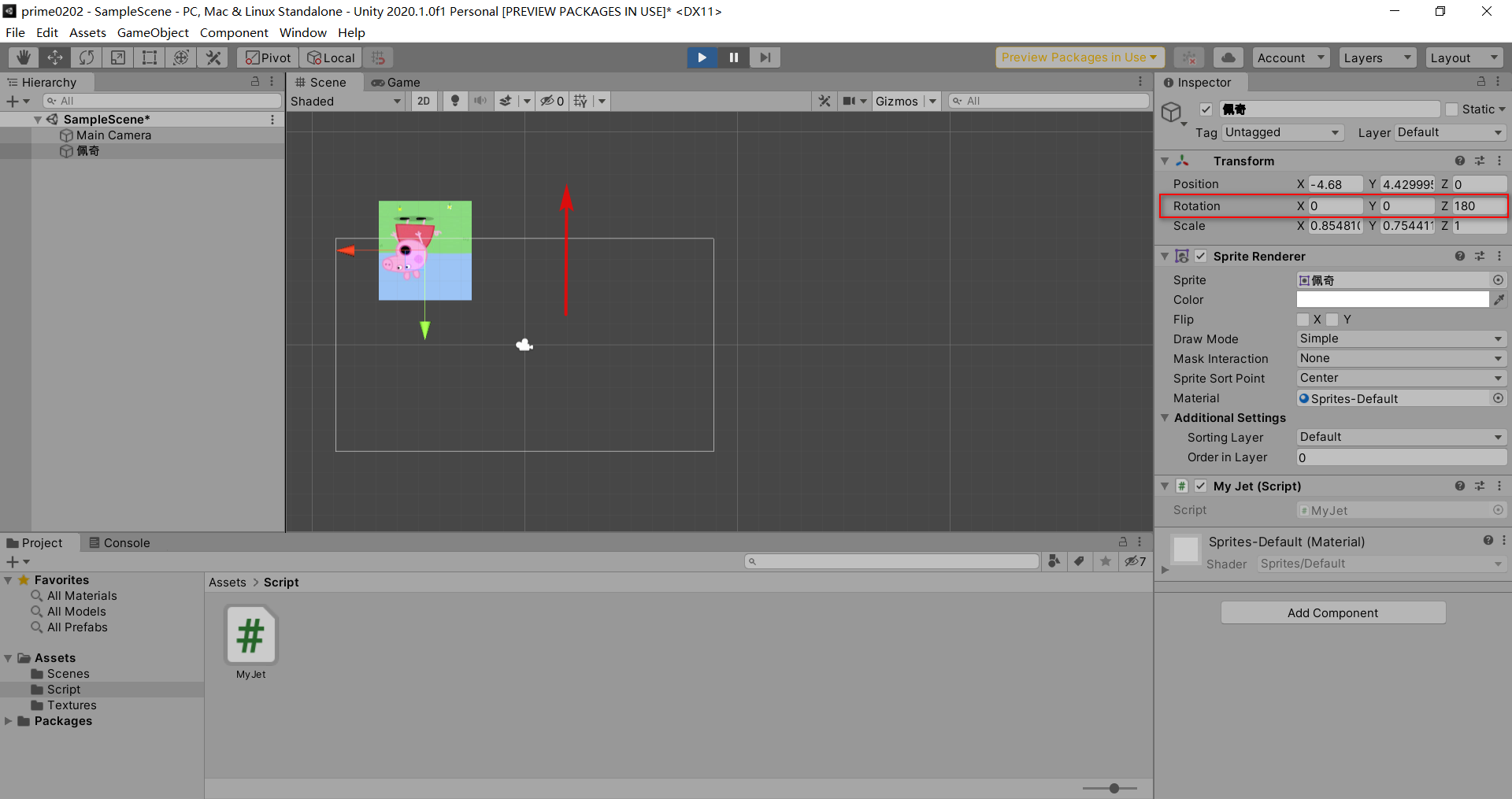
Unity3D -知识点(1)
1.场景视图鼠标滚轮:场景放大缩小鼠标右键:场景左右平移场景编辑器中,能看到什么?网格,每一格大小为1unit,建模不同,规定不同,(对应屏幕上100个像素)世界坐标系y轴向上为正x轴向右为…...

【学习笔记】NOIP暴零赛3
博弈(game) 观察到博弈过程中胜负态不会发生改变,那么求出从每个棋子出发能走的最长链,然后背包即可。 复杂度O(nm)O(nm)O(nm)。 #include<bits/stdc.h> #define ll long long #define pb push_back using namespace std; const int mod9982443…...

Java JSR规范列表
Java JSR规范列表目录概述需求:设计思路实现思路分析1.JSR2.JSR方法3.web service4.Webservice:5.数据处理器拓展实现参考资料和推荐阅读Survive by day and develop by night. talk for import biz , show your perfect code,full busy,skip hardness,m…...

Java必备小知识点1
Java程序类型: Applications和AppletApplications:是指在计算机操作系统中运行的程序。是完整的程序,能独立运行。被编译后,用普通的Java解释器就可以使其边解释边执行。必定含有一个main方法,程序执行时,首先寻找main方法&#x…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

并发编程 - go版
1.并发编程基础概念 进程和线程 A. 进程是程序在操作系统中的一次执行过程,系统进行资源分配和调度的一个独立单位。B. 线程是进程的一个执行实体,是CPU调度和分派的基本单位,它是比进程更小的能独立运行的基本单位。C.一个进程可以创建和撤销多个线程;同一个进程中…...

为什么要创建 Vue 实例
核心原因:Vue 需要一个「控制中心」来驱动整个应用 你可以把 Vue 实例想象成你应用的**「大脑」或「引擎」。它负责协调模板、数据、逻辑和行为,将它们变成一个活的、可交互的应用**。没有这个实例,你的代码只是一堆静态的 HTML、JavaScript 变量和函数,无法「活」起来。 …...

【Post-process】【VBA】ETABS VBA FrameObj.GetNameList and write to EXCEL
ETABS API实战:导出框架元素数据到Excel 在结构工程师的日常工作中,经常需要从ETABS模型中提取框架元素信息进行后续分析。手动复制粘贴不仅耗时,还容易出错。今天我们来用简单的VBA代码实现自动化导出。 🎯 我们要实现什么? 一键点击,就能将ETABS中所有框架元素的基…...

DiscuzX3.5发帖json api
参考文章:PHP实现独立Discuz站外发帖(直连操作数据库)_discuz 发帖api-CSDN博客 简单改造了一下,适配我自己的需求 有一个站点存在多个采集站,我想通过主站拿标题,采集站拿内容 使用到的sql如下 CREATE TABLE pre_forum_post_…...

js 设置3秒后执行
如何在JavaScript中延迟3秒执行操作 在JavaScript中,要设置一个操作在指定延迟后(例如3秒)执行,可以使用 setTimeout 函数。setTimeout 是JavaScript的核心计时器方法,它接受两个参数: 要执行的函数&…...

在Zenodo下载文件 用到googlecolab googledrive
方法:Figshare/Zenodo上的数据/文件下载不下来?尝试利用Google Colab :https://zhuanlan.zhihu.com/p/1898503078782674027 参考: 通过Colab&谷歌云下载Figshare数据,超级实用!!࿰…...
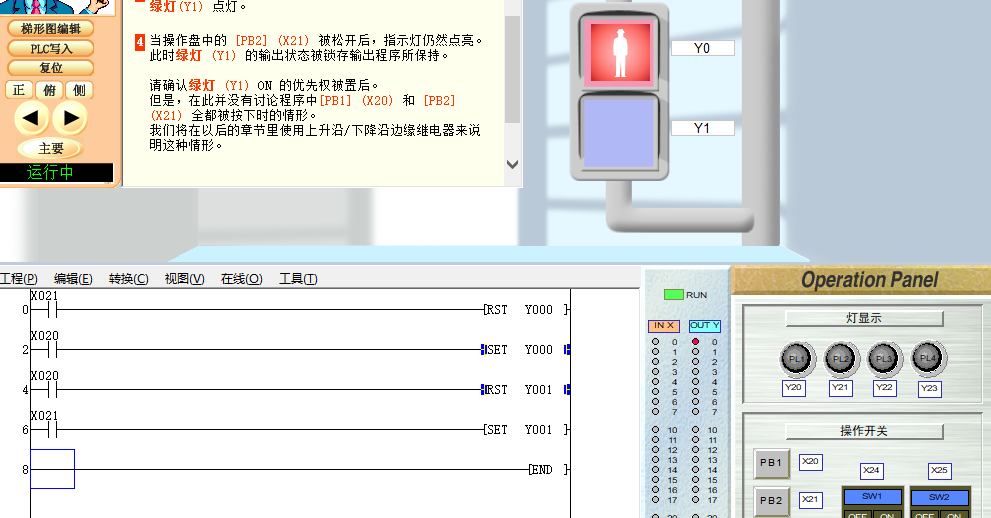
PLC入门【4】基本指令2(SET RST)
04 基本指令2 PLC编程第四课基本指令(2) 1、运用上接课所学的基本指令完成个简单的实例编程。 2、学习SET--置位指令 3、RST--复位指令 打开软件(FX-TRN-BEG-C),从 文件 - 主画面,“B: 让我们学习基本的”- “B-3.控制优先程序”。 点击“梯形图编辑”…...
