代码随想录算法训练营day56
文章目录
- Day56
- 两个字符串的删除操作
- 题目
- 思路
- 代码
- 编辑距离
- 题目
- 思路
- 代码
Day56
两个字符串的删除操作
583. 两个字符串的删除操作 - 力扣(LeetCode)
题目
给定两个单词 word1 和 word2,找到使得 word1 和 word2 相同所需的最小步数,每步可以删除任意一个字符串中的一个字符。
示例:
- 输入: “sea”, “eat”
- 输出: 2
- 解释: 第一步将"sea"变为"ea",第二步将"eat"变为"ea"
思路
本题和动态规划:115.不同的子序列 (opens new window)相比,其实就是两个字符串都可以删除了,情况虽说复杂一些,但整体思路是不变的。
这次是两个字符串可以相互删了,这种题目也知道用动态规划的思路来解
动规五部曲
- 确定dp数组(dp table)以及下标的含义
dp[i][j]:以i-1为结尾的字符串word1,和以j-1位结尾的字符串word2,想要达到相等,所需要删除元素的最少次数。
- 确定递推公式
- 当word1[i - 1] 与 word2[j - 1]相同的时候
- 当word1[i - 1] 与 word2[j - 1]不相同的时候
当word1[i - 1] 与 word2[j - 1]相同的时候,dp[i][j] = dp[i - 1][j - 1];
当word1[i - 1] 与 word2[j - 1]不相同的时候,有三种情况:
情况一:删word1[i - 1],最少操作次数为dp[i - 1][j] + 1
情况二:删word2[j - 1],最少操作次数为dp[i][j - 1] + 1
情况三:同时删word1[i - 1]和word2[j - 1],操作的最少次数为dp[i - 1][j - 1] + 2
那最后当然是取最小值,所以当word1[i - 1] 与 word2[j - 1]不相同的时候,递推公式:dp[i][j] = min({dp[i - 1][j - 1] + 2, dp[i - 1][j] + 1, dp[i][j - 1] + 1});
因为 dp[i][j - 1] + 1 = dp[i - 1][j - 1] + 2,所以递推公式可简化为:dp[i][j] = min(dp[i - 1][j] + 1, dp[i][j - 1] + 1);
这里可能不少录友有点迷糊,从字面上理解 就是 当 同时删word1[i - 1]和word2[j - 1],dp[i][j-1] 本来就不考虑 word2[j - 1]了,那么我在删 word1[i - 1],是不是就达到两个元素都删除的效果,即 dp[i][j-1] + 1。
- dp数组如何初始化
从递推公式中,可以看出来,dp[i][0] 和 dp[0][j]是一定要初始化的。
dp[i][0]:word2为空字符串,以i-1为结尾的字符串word1要删除多少个元素,才能和word2相同呢,很明显dp[i][0] = i。
for(int i = 1; i < len1 + 1; i++) dp[i][0] = i;for(int j = 1; j < len2 + 1; j++) dp[0][j] = j;dp[0][0] = 0;
- 确定遍历顺序
从递推公式 dp[i][j] = min(dp[i - 1][j - 1] + 2, min(dp[i - 1][j], dp[i][j - 1]) + 1); 和dp[i][j] = dp[i - 1][j - 1]可以看出dp[i][j]都是根据左上方、正上方、正左方推出来的。
所以遍历的时候一定是从上到下,从左到右,这样保证dp[i][j]可以根据之前计算出来的数值进行计算。
- 举例推导dp数组
代码
class Solution {public int minDistance(String word1, String word2) {int len1 = word1.length();int len2 = word2.length();int dp[][] = new int[len1 + 1][len2 + 1];for(int i = 1; i < len1 + 1; i++) dp[i][0] = i;for(int j = 1; j < len2 + 1; j++) dp[0][j] = j;dp[0][0] = 0;for(int i = 1; i < len1 + 1; i++){for(int j = 1; j < len2 + 1; j++){if(word1.charAt(i - 1) == word2.charAt(j - 1)){dp[i][j] = dp[i - 1][j - 1];}else{dp[i][j] = Math.min(dp[i - 1][j - 1] + 2, Math.min(dp[i][j - 1], dp[i - 1][j]) + 1);}}}return dp[len1][len2];}
}
编辑距离
72. 编辑距离 - 力扣(LeetCode)
题目
给你两个单词 word1 和 word2,请你计算出将 word1 转换成 word2 所使用的最少操作数 。
你可以对一个单词进行如下三种操作:
- 插入一个字符
- 删除一个字符
- 替换一个字符
- 示例 1:
- 输入:word1 = “horse”, word2 = “ros”
- 输出:3
- 解释: horse -> rorse (将 ‘h’ 替换为 ‘r’) rorse -> rose (删除 ‘r’) rose -> ros (删除 ‘e’)
- 示例 2:
- 输入:word1 = “intention”, word2 = “execution”
- 输出:5
- 解释: intention -> inention (删除 ‘t’) inention -> enention (将 ‘i’ 替换为 ‘e’) enention -> exention (将 ‘n’ 替换为 ‘x’) exention -> exection (将 ‘n’ 替换为 ‘c’) exection -> execution (插入 ‘u’)
提示:
- 0 <= word1.length, word2.length <= 500
- word1 和 word2 由小写英文字母组成
思路
编辑距离是用动规来解决的经典题目,这道题目看上去好像很复杂,但用动规可以很巧妙的算出最少编辑距离。
动规五部曲
- 确定dp数组(dp table)以及下标的含义
dp[i][j] 表示以下标i-1为结尾的字符串word1,和以下标j-1为结尾的字符串word2,最近编辑距离为dp[i][j]。
- 确定递推公式
在确定递推公式的时候,首先要考虑清楚编辑的几种操作,整理如下:
if (word1[i - 1] == word2[j - 1])不操作
if (word1[i - 1] != word2[j - 1])增删换
在整个动规的过程中,最为关键就是正确理解dp[i][j]的定义!
if (word1[i - 1] == word2[j - 1]) 那么说明不用任何编辑,dp[i][j] 就应该是 dp[i - 1][j - 1],即dp[i][j] = dp[i - 1][j - 1];
if (word1[i - 1] != word2[j - 1]),此时就需要编辑了,如何编辑呢?
- 操作一:word1删除一个元素,那么就是以下标i - 2为结尾的word1 与 j-1为结尾的word2的最近编辑距离 再加上一个操作。
即 dp[i][j] = dp[i - 1][j] + 1;
- 操作二:word2删除一个元素,那么就是以下标i - 1为结尾的word1 与 j-2为结尾的word2的最近编辑距离 再加上一个操作。
即 dp[i][j] = dp[i][j - 1] + 1;
这里有同学发现了,怎么都是删除元素,添加元素去哪了。
word2添加一个元素,相当于word1删除一个元素,例如 word1 = "ad" ,word2 = "a",word1删除元素'd' 和 word2添加一个元素'd',变成word1="a", word2="ad", 最终的操作数是一样!
- 操作三:替换元素,
word1替换word1[i - 1],使其与word2[j - 1]相同,此时不用增删加元素。
可以回顾一下,if (word1[i - 1] == word2[j - 1])的时候我们的操作 是 dp[i][j] = dp[i - 1][j - 1] 对吧。
那么只需要一次替换的操作,就可以让 word1[i - 1] 和 word2[j - 1] 相同。
所以 dp[i][j] = dp[i - 1][j - 1] + 1;
综上,当 if (word1[i - 1] != word2[j - 1]) 时取最小的,即:dp[i][j] = min({dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]}) + 1;
if(word1.charAt(i - 1) == word2.charAt(j - 1)){dp[i][j] = dp[i - 1][j - 1];
}else{dp[i][j] = Math.min(dp[i - 1][j - 1], Math.min(dp[i - 1][j], dp[i][j - 1])) + 1;
}
- dp数组如何初始化
dp[i][j] 表示以下标i-1为结尾的字符串word1,和以下标j-1为结尾的字符串word2,最近编辑距离为dp[i][j]。
那么dp[i][0] 和 dp[0][j] 表示什么呢?
dp[i][0] :以下标i-1为结尾的字符串word1,和空字符串word2,最近编辑距离为dp[i][0]。
那么dp[i][0]就应该是i,对word1里的元素全部做删除操作,即:dp[i][0] = i;
同理dp[0][j] = j;
dp[0][0] = 0 空字符串和空字符串不需要操作就相等
for(int i = 0; i < word1.length() + 1; i++) dp[i][0] = i;for(int j = 0; j < word2.length() + 1; j++) dp[0][j] = j;dp[0][0] = 0;
- 确定遍历顺序
从如下四个递推公式:
dp[i][j] = dp[i - 1][j - 1]dp[i][j] = dp[i - 1][j - 1] + 1dp[i][j] = dp[i][j - 1] + 1dp[i][j] = dp[i - 1][j] + 1
可以看出dp[i][j]是依赖左方,上方和左上方元素的,如图:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-nByVxeHF-1691224926511)(https://code-thinking-1253855093.file.myqcloud.com/pics/20210114162113131.jpg “72.编辑距离”)]
for(int i = 1; i < word1.length() + 1; i++){for(int j = 1; j < word2.length() + 1; j++){if(word1.charAt(i - 1) == word2.charAt(j - 1)){dp[i][j] = dp[i - 1][j - 1];}else{dp[i][j] = Math.min(dp[i - 1][j - 1], Math.min(dp[i - 1][j], dp[i][j - 1])) + 1;}}}
- 举例推导dp数组
代码
class Solution {public int minDistance(String word1, String word2) {// dp[i][j] 表示以下标i-1为结尾的字符串word1,和以下标j-1为结尾的字符串word2,最近编辑距离为dp[i][j]。int dp[][] = new int[word1.length() + 1][word2.length() + 1];for(int i = 0; i < word1.length() + 1; i++) dp[i][0] = i;for(int j = 0; j < word2.length() + 1; j++) dp[0][j] = j;dp[0][0] = 0;for(int i = 1; i < word1.length() + 1; i++){for(int j = 1; j < word2.length() + 1; j++){if(word1.charAt(i - 1) == word2.charAt(j - 1)){dp[i][j] = dp[i - 1][j - 1];}else{// 操作一:word1删除一个元素,那么就是以下标i - 2为结尾的word1 与 j-1为结尾的word2的最近编辑距离 再加上一个操作。 dp[i - 1][j] + 1;// 操作二:word2删除一个元素,那么就是以下标i - 1为结尾的word1 与 j-2为结尾的word2的最近编辑距离 再加上一个操作。 dp[i][j - 1] + 1// 操作三:替换元素,word1替换word1[i - 1],使其与word2[j - 1]相同,此时不用增删加元素。 dp[i - 1][j - 1] + 1dp[i][j] = Math.min(dp[i - 1][j - 1], Math.min(dp[i - 1][j], dp[i][j - 1])) + 1;}}}return dp[word1.length()][word2.length()];}
}
相关文章:

代码随想录算法训练营day56
文章目录 Day56两个字符串的删除操作题目思路代码 编辑距离题目思路代码 Day56 两个字符串的删除操作 583. 两个字符串的删除操作 - 力扣(LeetCode) 题目 给定两个单词 word1 和 word2,找到使得 word1 和 word2 相同所需的最小步数&#…...

通话降噪算法在手机和IOT设备上的应用和挑战
随着电子产品的升级换代,用户对通话质量的要求也越来越高。通话降噪算法对通话质量起到了关键核心的作用。计算资源的提升使得深度学习模型在便携式的低功耗芯片上面跑起来了,器件成本降低让IoT设备开始使用骨导传感器,,那怎么样才…...
Pet Detection System (PDS)
宠物医院检验设备物联系统...
+cv2.threshold())
【OpenCV常用函数:颜色空间转换、阈值化】cv2.cvtColor()+cv2.threshold()
1、cv2.cvtColor() 对图像进行颜色空间的转换 cv2.cvtColor(src, code[, dst[, dstCn]])1) src: 输入图像 2) code: 颜色空间转换编码,常使用的GRAY和RGB之间的转换 cv2.COLOR_BGR2GRAY, cv2.COLOR_RGB2GRAY, cv2.COLOR_GRAY2BGR, cv2.COLOR_GRAY2RGB 3) dst: 输出…...

一键登录和短信验证登录,到底有什么区别?
一键登录是什么? 本机号码一键登录验证是一种登录认证方式,通过获取用户手机上的本机号码来验证用户身份,从而实现快捷登录和简化登录流程的目的。 在使用一键登录时,首先需要用户在登录页面选择使用本机号码一键登录࿰…...

史上最精简Android RecyclerView实现拖拽排序改变位置代码
要实现RecyclerView的长按拖动改变位置,可以使用ItemTouchHelper类来处理拖动和滑动的操作。下面演示如何实现长按拖动改变位置: 首先,在你的Activity或Fragment中,初始化RecyclerView和ItemTouchHelper: RecyclerVi…...
centos 7 系统上重启 mysql 时报错 Failed to restart mysqld.service: Unit not found.
在 centos 7 系统上,使用常规命令:systemctl restart mysql 或 service mysqld restart 重启 mysql 时都会报如下错误: Failed to start mysqld.service: Unit not found. 根据所报错误,在网上搜罗了一圈,未果&#x…...

时间复杂度空间复杂度相关练习题
1.消失的数字 【题目】:题目链接 思路1:排序——》qsort快排——》时间复杂度O(n*log2n) 不符合要求 思路2:(0123...n)-(a[0]a[1][2]...a[n-2]) ——》 时间复杂度O(N)空间复杂度…...

Linux | Ubuntu18.04安装RTX 4060显卡驱动完整教程
文章目录 概述一、定义介绍二、操作教程(一)、前期准备1.进入终端界面2.关闭界面显示器3.禁用其他显卡驱动4.卸载残余显卡驱动5.下载驱动(二)、安装驱动1.给驱动程序赋予权限2.安装驱动3.检查结果(三)、后续问题1.黑屏问题概述 本节详细介绍了如何在ubuntu18系统安装4060显卡的…...
Mermaid语法使用
Mermaid语法使用 1. 基础类1.1 流程图1.2 时序图 2. 工程图2.1 类图2.2 Git图 1. 基础类 1.1 流程图 graph TBid1(圆角矩形)--普通线-->id2[矩形];subgraph 子图id2粗线>id3{菱形}id3-. 虚线.->id4>右向旗帜]id3--无箭头---id5((圆形))end方向定义 用词含义TB从…...
[OnWork.Tools]系列 05-系统工具
简介 系统工具主要是将Window常用工具的快捷启动的集合 双击快速启动 计算器,记事本,截图,画图工具 控制面板,服务管理,关闭显示器,关机 启动文件夹,我的电脑,管理工具 右键菜单 添加快捷方式到桌面...

SOME/IP学习笔记1
SOA概念 在SOA中,每个服务就好像我们每一个人在社会中扮演的角色,在对别人提供着服务的同时,同时也享受着别人提供出来的服务,人与人之间,既是彼此独立的,又是需要互相通讯的。服务提供者将功能具象为一组接口,这样使用者就能知道如何调用服务,完成某件事情,得到某个…...

Effective Java笔记(26)请不要使用原生态类型
首先介绍一些术语 。 声明中具有一个或者多个类型参数( type parameter )的类或者接口,就是泛型( generic )类或者接口 。 例如,List 接口就只有单个类型参数 E ,表示列表的元素类型 。这个接口…...

linux 内存 - KO内存占用
说明 KO(kernel module)占用的内存分为两部分: 静态占用 :ko insmod时系统固定分配的内存。动态申请 :代码中动态申请的内存,由于申请方式不同,统计的方式也可能不同,例如:使用vmalloc和kmall…...
2023.8.7论文阅读
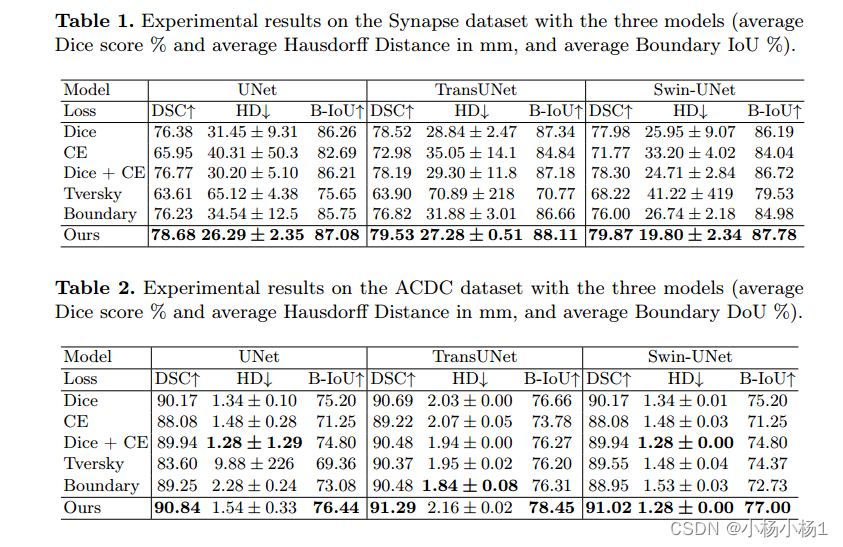
文章目录 CMUNeXt: An Efficient Medical Image Segmentation Network based on Large Kernel and Skip Fusion摘要本文方法实验结果 Boundary Difference Over Union Loss For Medical Image Segmentation(损失函数)摘要本文方法实验结果 CMUNeXt: An E…...
2023河南萌新联赛第(五)场:郑州轻工业大学 --Kruskal
题目描述 给定一张nnn个点的无向完全图,其中两点之间的路径边权为两点编号的按位与(编号为 (1,2,...,n)(1,2,...,n)(1,2,...,n)),即w(u,v)u&v(1≤u,v≤n)w\left(u, v \right )u\&v \left( 1 \le u, v \le n \right)w(u,v…...
Maven引入本地jar包
maven做为一种强大的依赖管理工具,可以帮助我们更方便的管理项目中的依赖;而在使用过程中我们难免会有需要引入本地jar包的需求,这里踩过坑之后我分享俩种引入方式; 1.上传jar到本地maven仓库,再引入 使用此方法后可…...

Java并发编程实战——结构化并发应用程序
文章目录 6 任务执行6.1 在线程中执行任务6.1.1 串行地执行任务6.1.2 显式地为任务创建线程6.1.3 无限制创建线程的不足 6.2 Executor框架6.2.1 示例:基于Executor的Web服务器6.2.2 执行策略6.2.3 线程池6.2.4 Executor的生命周期6.2.5 延迟任务与周期任务 6.3 找出…...
uniapp echarts 点击失效
这个问题网上搜了一堆,有的让你降版本,有的让你改源码。。。都不太符合预期,目前我的方法可以用最新的echarts。 这个方法就是由npm安装转为CDN,当然你可能会质疑用CDN这样会不稳定,那如果CDN的地址是本地呢࿱…...
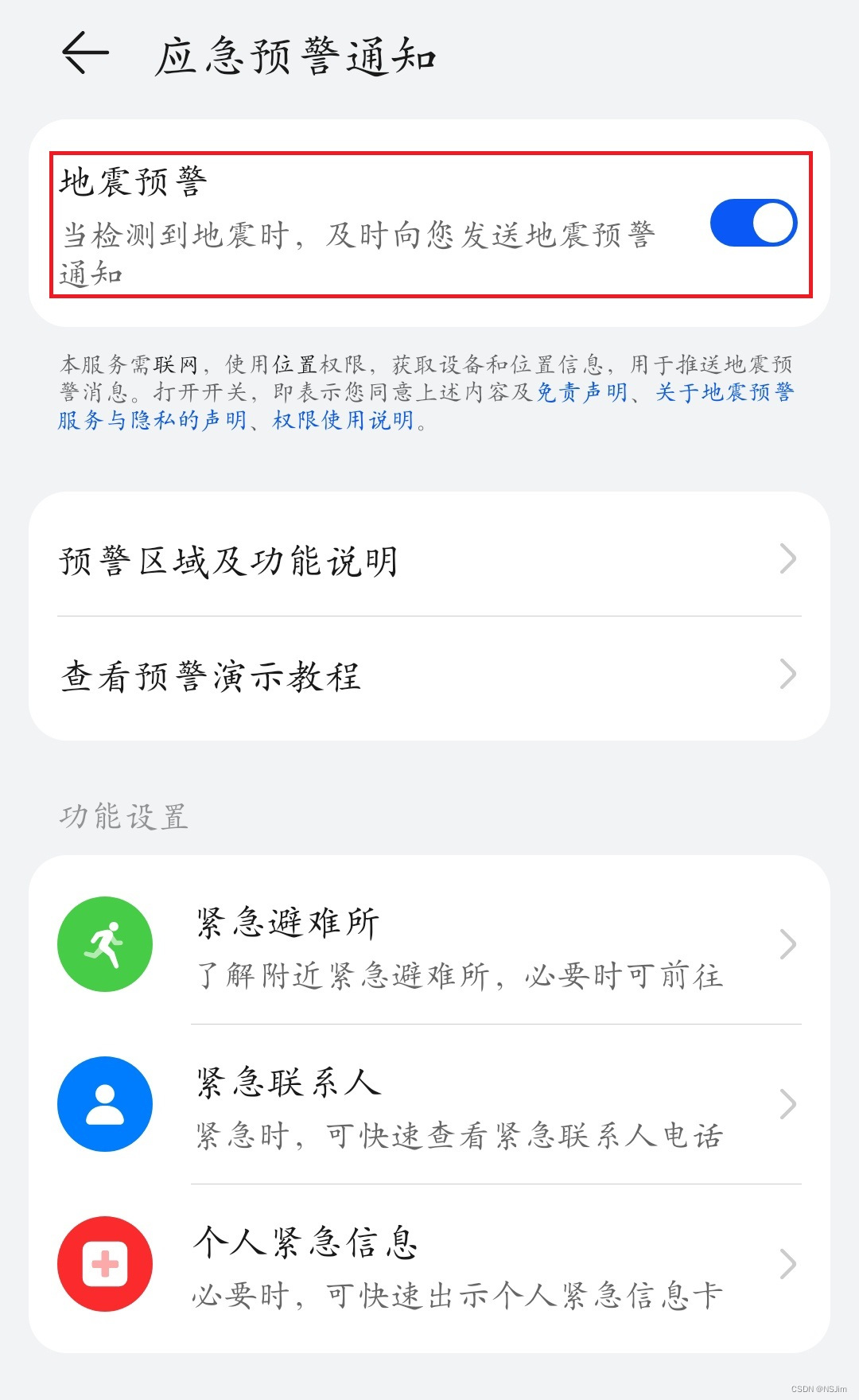
手机开启应急预警通知 / 地震预警
前言 安卓手机在检测到地震时,将发送地震预警通知,但此设置是默认关闭的,原因是以防引发用户恐慌从而引发安全问题,且开启此设置需要完成指引教程,因此默认关闭此设置。下文介绍如何开启此设置。 开启方法 华为手机开…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

Web中间件--tomcat学习
Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机,它可以执行Java字节码。Java虚拟机是Java平台的一部分,Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...

tomcat入门
1 tomcat 是什么 apache开发的web服务器可以为java web程序提供运行环境tomcat是一款高效,稳定,易于使用的web服务器tomcathttp服务器Servlet服务器 2 tomcat 目录介绍 -bin #存放tomcat的脚本 -conf #存放tomcat的配置文件 ---catalina.policy #to…...

手机平板能效生态设计指令EU 2023/1670标准解读
手机平板能效生态设计指令EU 2023/1670标准解读 以下是针对欧盟《手机和平板电脑生态设计法规》(EU) 2023/1670 的核心解读,综合法规核心要求、最新修正及企业合规要点: 一、法规背景与目标 生效与强制时间 发布于2023年8月31日(OJ公报&…...

深入理解Optional:处理空指针异常
1. 使用Optional处理可能为空的集合 在Java开发中,集合判空是一个常见但容易出错的场景。传统方式虽然可行,但存在一些潜在问题: // 传统判空方式 if (!CollectionUtils.isEmpty(userInfoList)) {for (UserInfo userInfo : userInfoList) {…...

通过 Ansible 在 Windows 2022 上安装 IIS Web 服务器
拓扑结构 这是一个用于通过 Ansible 部署 IIS Web 服务器的实验室拓扑。 前提条件: 在被管理的节点上安装WinRm 准备一张自签名的证书 开放防火墙入站tcp 5985 5986端口 准备自签名证书 PS C:\Users\azureuser> $cert New-SelfSignedCertificate -DnsName &…...

elementUI点击浏览table所选行数据查看文档
项目场景: table按照要求特定的数据变成按钮可以点击 解决方案: <el-table-columnprop"mlname"label"名称"align"center"width"180"><template slot-scope"scope"><el-buttonv-if&qu…...
