C++中访问存储在数组中的数据
C++中访问存储在数组中的数据
要访问数组中的元素,可使用从零开始的索引。这些索引之所以被称为从零开始的,是因为数组中第一个元素的索引为零。因此,存储在数组 myNumbers 中的第一个整数值为 myNumbers[0],第二个为 myNumbers[1],依此类推。第 5 个元素为 myNumbers[4],换句话说,数组中最后一个元素的索引总是比数组长度少 1。
被要求访问索引为 N 的元素时,编译器以第一个元素(索引为零)的内存地址为起点,加上偏移量 N*sizeof(element),即向前跳 N 个元素,到达包含第 N+1 个元素的地址。 C++编译器不会检查索引是否在数组的范围内,您可从只包含 10 个元素的数组中取回索引为 1001 的元素,但这样做将给程序带来安全和稳定性方面的风险。访问数组时,确保不超越其边界是程序员的职责。
警告:
访问数组时,如果超越其边界,结果将是无法预料的。在很多情况下,这将导致程序崩溃。应不惜一切代价避免访问数组时超越其边界。
以下程序演示了如何声明一个 int 数组、初始化其元素并将元素的值显示到屏幕上:
#include <iostream>using namespace std;int main ()
{int myNumbers [5] = {34, 56, -21, 5002, 365};cout << "First element at index 0: " << myNumbers [0] << endl;cout << "Second element at index 1: " << myNumbers [1] << endl;cout << "Third element at index 2: " << myNumbers [2] << endl;cout << "Fourth element at index 3: " << myNumbers [3] << endl;cout << "Fifth element at index 4: " << myNumbers [4] << endl;return 0;
}
输出:
First element at index 0: 34
Second element at index 1: 56
Third element at index 2: -21
Fourth element at index 3: 5002
Fifth element at index 4: 365
分析:
第 6 行声明了一个包含 5 个 int 元素的数组,并给每个元素指定了初始值。接下来的几行代码使用 cout、数组变量 myNumbers 和合适的索引显示这些整数。
注意:
用于访问数组元素的索引从零开始
该文章会更新,欢迎大家批评指正。
推荐一个零声学院免费公开课程,个人觉得老师讲得不错,
分享给大家:Linux,Nginx,ZeroMQ,MySQL,Redis,
fastdfs,MongoDB,ZK,流媒体,CDN,P2P,K8S,Docker,
TCP/IP,协程,DPDK等技术内容,点击立即学习:
服务器课程:C++服务器
相关文章:

C++中访问存储在数组中的数据
C中访问存储在数组中的数据 要访问数组中的元素,可使用从零开始的索引。这些索引之所以被称为从零开始的,是因为数组中第一个元素的索引为零。因此,存储在数组 myNumbers 中的第一个整数值为 myNumbers[0],第二个为 myNumbers[1]…...

【创建型设计模式】C#设计模式之原型模式
原型模式是一种创建型设计模式,它通过复制现有对象来创建新对象,而无需通过实例化的方式。它允许我们使用已经存在的对象作为蓝本,从而创建新的对象,这样可以避免重复初始化相似的对象,提高了对象的创建效率。 现在给…...
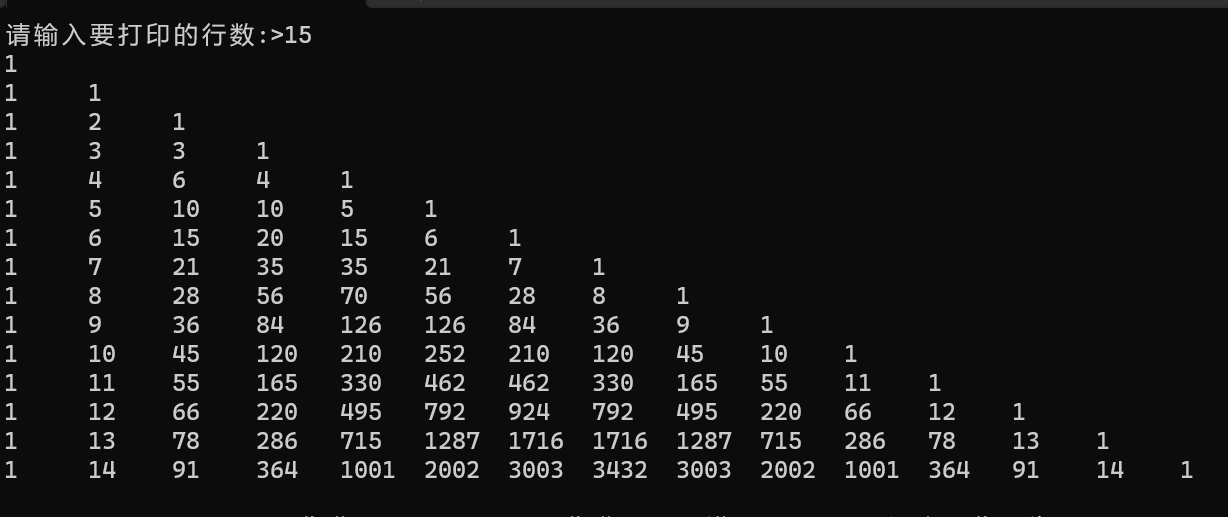
用C语言高效地打印杨辉三角
假设杨辉三角的通项公式为a(n),则打印形式如下: 然而我们知道,它应该是这样的: 三角形两边的值都为1,且每个元素的值都为该元素正上方和其正上方前面的元素的值之和。 为了实现这个代码,我们需要知道每行首…...

TCP/IP四层模型对比OSI七层网络模型的区别是啥?数据传输过程原来是这样的
一、TCP/IP四层模型对比OSI七层模型 它们两个定义的一些功能和协议都是差不多的。TCP/IP四层协议模型比我们的七层少了三层,把我们的数据链路层和物理层放在一层里面了,叫做数据链路层(网络接口层),对应网络协议也没有…...
接口测试实战,Jmeter正则提取响应数据-详细整理,一篇打通...
目录:导读 前言一、Python编程入门到精通二、接口自动化项目实战三、Web自动化项目实战四、App自动化项目实战五、一线大厂简历六、测试开发DevOps体系七、常用自动化测试工具八、JMeter性能测试九、总结(尾部小惊喜) 前言 在测试时…...

基于自适应变异粒子群优化BP神经网络 的风速预测,基于IPSO-BP神经网络里的风速预测
目录 摘要 BP神经网络的原理 BP神经网络的定义 BP神经网络的基本结构 BP神经网络的神经元 BP神经网络的激活函数, BP神经网络的传递函数 粒子群算法的原理及步骤 基于自适应变异粒子群算法改进优化BP神经网络的风速预测 完整代码下载:https://download.csdn.net/download/ab…...
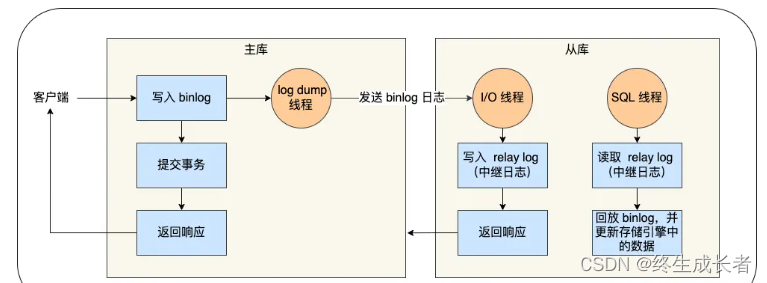
MySQL—日志
这里写目录标题 undo logundo log的作用undo log页记录的是什么 Buffer Pool为什么需要Buffer PoolBuffer Pool缓存什么 redo log什么是redo logredo log的作用redo log什么时候刷盘undo和redo的区别 binlogbinlog 作用redo log和binlog区别如果数据数据被删了,能用…...

uniapp 扩展组件 uni-forms 的表单验证之 validateFunction 只响应一次
uniapp 扩展组件 uni-forms 的表单验证之 validateFunction 只响应一次 问题代码官方说明参考资料 问题代码 直接从官方示例中复制过来改的。为了演示 <template><view><uni-forms ref"form" :modelValue"formData" :rules"rules&qu…...

每日一题8.10 lc39
39. 组合总和 给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ,找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ,并以列表形式返回。你可以按 任意顺序 返回这些组合。 candidates 中的 同一个 数字可以 无限制重…...

贝叶斯深度学习的温和介绍
一、说明 欢迎来到令人兴奋的概率编程世界!本文是对这个领域的温和介绍,你只需要对深度学习和贝叶斯统计有一个基本的了解。如果像我一样,你听说过贝叶斯深度学习,并且你猜它涉及贝叶斯统计,但你不知道它是如何使用的&…...

无涯教程-Perl - glob函数
描述 此函数返回与EXPR匹配的文件的列表,这些文件将由标准Bourne shell进行扩展。如果EXPR未指定路径,请使用当前目录。如果省略EXPR,则使用$_的值。 从Perl 5.6开始,扩展是在内部完成的,而不是使用外部脚本。扩展遵循csh(以及任何派生形式,包括tcsh和bash)的扩展方式,其翻译…...

前端先行模拟接口(mock+expres+json)
目录 mock模拟数据:data/static.js 路由:index.js 服务器:server.js yarn /node 启动服务器:yarn start 客户端:修改代理路径(修改设置后都要重启才生效) 示例 后端框架express构建服务器 前端发起请求 静态数…...
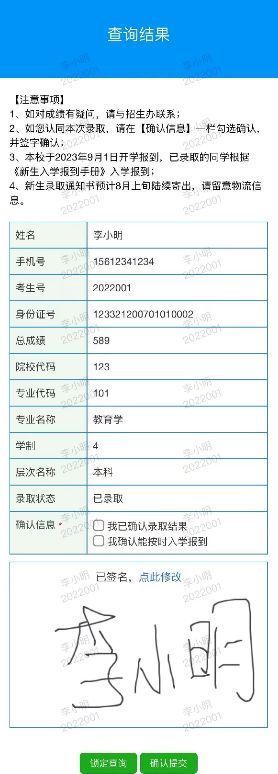
老师如何制作学生分班信息查询系统?
即将迎来新学期的开始!学校和老师们将忙于为我们可爱的学生做分班准备。如果有一个强大的分班查询系统,学生们就可以提前知道自己被分到哪个班级,有哪些课程,以及班主任是谁! 别担心,我将教你如何设计一个…...

Java实战:高效提取PDF文件指定坐标的文本内容
前言 临时接到一个紧急需要处理的事项。业务侧一个同事有几千个PDF文件需要整理:需要从文件中的指定位置获取对应的编号和地址。 要的急,工作量大。所以就问到技术部有没有好的解决方案。 问技术的话就只能写个demo跑下了。 解决办法 1. 研究下PDF文档…...

centos磁盘满了,怎么清理大文件
当CentOS磁盘空间不足时,可以通过以下步骤清理大文件: 确定磁盘使用情况:运行以下命令查看磁盘使用情况和占用空间最大的文件或目录: df -h du -sh /*清理临时文件:运行以下命令清理临时文件夹中的过期数据ÿ…...

AIGC:【LLM(四)】——LangChain+ChatGLM:本地知识库问答方案
文章目录 一.文件加载与分割二.文本向量化与存储1.文本向量化(embedding)2.存储到向量数据库 三.问句向量化四.相似文档检索五.prompt构建六.答案生成 LangChainChatGLM项目(https://github.com/chatchat-space/langchain-ChatGLM)实现原理如下图所示 (与基于文档的问答 大同小…...
企业在线产品手册可以这样做,小白也能轻松上手
企业在线产品手册是为了方便用户了解和使用企业产品而设计的一种在线文档。它的目标是提供清晰、简洁、易于理解的产品信息,使用户能够轻松上手,并最大限度地发挥产品的功能和优势。 如何设计企业在线产品手册的建议和步骤: 目标用户分析&am…...
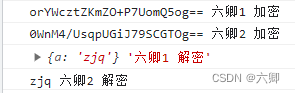
crypto-js中AES的加解密封装
在项目中安装依赖: npm i crypto-js在使用的页面引入: import CryptoJS from crypto-jscrypto-js中AES的加解密简单的封装了一下: //加密const KEY 000102030405060708090a0b0c0d0e0f // 秘钥 这两个需要和后端统一const IV 8a8c8fd8fe3…...

【计算机视觉】MoCo v2 讲解
在阅读本篇之前建议先学习: 【计算机视觉】MoCo 讲解 【计算机视觉】SimCLR 讲解 MoCo v2 论文信息 标题:Improved Baselines with Momentum Contrastive Learning 作者:Xinlei Chen 期刊: 发布时间与更新时间:2020.03.09 主题:计算机视觉、对比学习 arXiv:[2003.04297]…...

如何解决亚马逊银行账户验证问题?来看看这些技巧吧!
在开亚马逊店铺的过程中,想必不少卖家遇到了这么一个问题,那就是亚马逊卖家有的时候会收到亚马逊银行账户验证的消息,主要就是用来确保亚马逊卖家账户收款信息的安全性。 亚马逊银行账户验证是一个十分重要的问题,如果说这些问题…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...
