动手学深度学习Pytorch 4.4练习
1.这个多项式回归问题可以准确地解出吗?提⽰:使⽤线性代数。
可以,把多项式问题,用matlab的str2sym表示出来,再用solve求解。
2.考虑多项式的模型选择。
- 1. 绘制训练损失与模型复杂度(多项式的阶数)的关系图。观察到了什么?需要多少阶的多项式才能将训练损失减少到0?
画图代码(阶数1-100):
# 记得把max_degree改为100# 把train改成这个函数
def trainLossComplex(train_features,test_features,train_labels,test_labels,num_epochs=1000):loss=nn.MSELoss(reduction='none')input_shape=train_features.shape[-1]# 不设置偏置,因为我们已经在多项式中实现了它net = nn.Sequential(nn.Linear(input_shape,1,bias=False))batch_size=min(10,train_labels.shape[0])train_features=torch.tensor(train_features, dtype=torch.float32)test_features=torch.tensor(test_features, dtype=torch.float32)train_iter=d2l.load_array((train_features,train_labels.reshape(-1,1)),batch_size)test_iter=d2l.load_array((test_features,test_labels.reshape(-1,1)),batch_size,is_train=False)trainer=torch.optim.SGD(net.parameters(),lr=0.01)for epoch in range(num_epochs):d2l.train_epoch_ch3(net,train_iter,loss,trainer)return evaluate_loss(net,train_iter,loss),evaluate_loss(net,test_iter,loss)
trainLoss=[]
textLoss=[]
x=np.arange(1,100)
for i in np.arange(1,100):train_loss,text_loss=trainLossComplex(poly_features[:n_train, :i], poly_features[n_train:,:i],labels[:n_train],labels[n_train:])trainLoss.append(train_loss)textLoss.append(text_loss)
d2l.plot(x, y, xlabel='degree', ylabel='train_loss', legend=None, xlim=None,ylim=[1e-3+0.007,1*1e-2+0.005], xscale='linear', yscale='linear',fmts=('-', 'm--', 'g-.', 'r:'), figsize=(3.5, 2.5), axes=None)
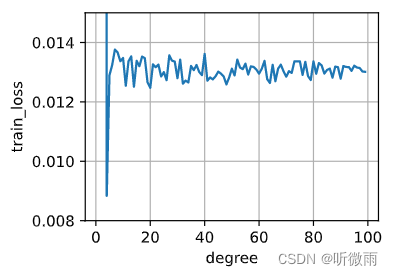
从图中看,1-100的阶数的多项式都不能把训练损失减少到0
- 2. 在这种情况下绘制测试的损失图。
d2l.plot(x, textLoss, xlabel='degree', ylabel='train_loss', legend=None, xlim=None,ylim=[1e-3,1.2], xscale='linear', yscale='linear',fmts=('-', 'm--', 'g-.', 'r:'), figsize=(3.5, 2.5), axes=None)
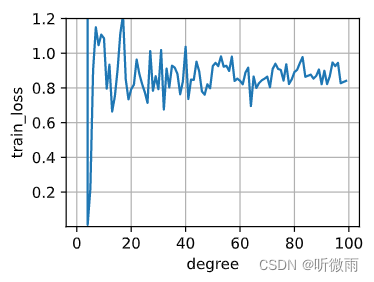
这里的值没有到0,只是图上看着到了
- 3. ⽣成同样的图,作为数据量的函数。
改一改数据量吧,再自己画一下吧,我太懒了,对不起
3. 如果不对多项式特征xi进⾏标准化(1/i!),会发⽣什么事情?能⽤其他⽅法解决这个问题吗?
如果有一个 x大于 1,那么这个很大的 i就会带来很大的值,优化的时候可能会带来很大的梯度值。
4. 泛化误差可能为零吗?
不太可能
相关文章:

动手学深度学习Pytorch 4.4练习
1.这个多项式回归问题可以准确地解出吗?提⽰:使⽤线性代数。 可以,把多项式问题,用matlab的str2sym表示出来,再用solve求解。 2.考虑多项式的模型选择。 1. 绘制训练损失与模型复杂度(多项式的阶数)的关系…...

【计算机视觉 | Kaggle】飞机凝结轨迹识别 Baseline 分享和解读(含源代码)
文章目录 一、导读二、比赛背景三、比赛任务四、比赛数据五、评价指标六、Baseline6.1 Training part6.2 Submission part 一、导读 比赛名称:Google Research - Identify Contrails to Reduce Global Warming https://www.kaggle.com/competitions/google-researc…...

ThinkPHP文件上传:简便安全的解决方案
在现代Web应用程序中,文件上传是一项常见而重要的功能。ThinkPHP是一种流行的PHP开发框架,提供了便捷而安全的文件上传解决方案。本文将介绍ThinkPHP框架中的文件上传功能,并探讨如何使用它来实现安全可靠的文件上传功能。 一、ThinkPHP文件…...

torch.multiprocessing
文章目录 张量共享torch.multiprocessing.spawnmultiprocessing.Pool与torch.multiprocessing.Pool阻塞非阻塞map阻塞非阻塞 starmap torch.multiprocessing是具有额外功能的multiprocessing,其 API 与multiprocessing完全兼容,因此我们可以将其用作直接…...

解决本地代码commit后发现远程分支被更新的烦恼!
解决本地代码commit后远程分支更新的烦恼! 在进行代码开发过程中,当我们准备将本地代码推送到远程分支时,有时会遇到远程分支已经被更新的情况。这给我们的开发工作带来了一些挑战,因为我们需要确保我们的修改与远程分支的更新保持…...
最新AI创作系统ChatGPT程序源码+详细搭建部署教程+微信公众号版+H5源码/支持GPT4.0+GPT联网提问/支持ai绘画+MJ以图生图+思维导图生成!
使用Nestjs和Vue3框架技术,持续集成AI能力到系统! 新增 MJ 官方图片重新生成指令功能同步官方 Vary 指令 单张图片对比加强 Vary(Strong) | Vary(Subtle)同步官方 Zoom 指令 单张图片无限缩放 Zoom out 2x | Zoom out 1.5x新增GPT联网提问功能、手机号注…...
)
910数据结构(2014年真题)
算法设计题 问题1 已知一个带头结点的单链表head,假设结点中的元素为整数,试编写算法:按递增次序输出单链表中各个结点的数据元素,并释放结点所占的存储空间。要求:(1)用文字给出你的算法思想;(2)不允许使…...
Idea创建maven管理的web项目
如果你想在项目中添加一个传统的 src 目录来存放源代码,可以按照以下步骤操作: 1. 在项目视图中,右键单击项目名称,选择 “New” -> “Directory”。 2. 在弹出的对话框中,输入目录名称为 “src”,然后…...
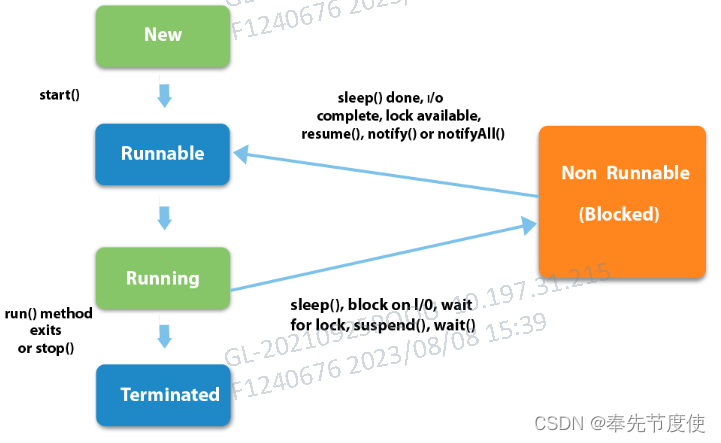
Java并发编程(一)多线程基础概念
概述 多线程技术:基于软件或者硬件实现多个线程并发执行的技术 线程可以理解为轻量级进程,切换开销远远小于进程 在多核CPU的计算机下,使用多线程可以更好的利用计算机资源从而提高计算机利用率和效率来应对现如今的高并发网络环境 并发编程…...
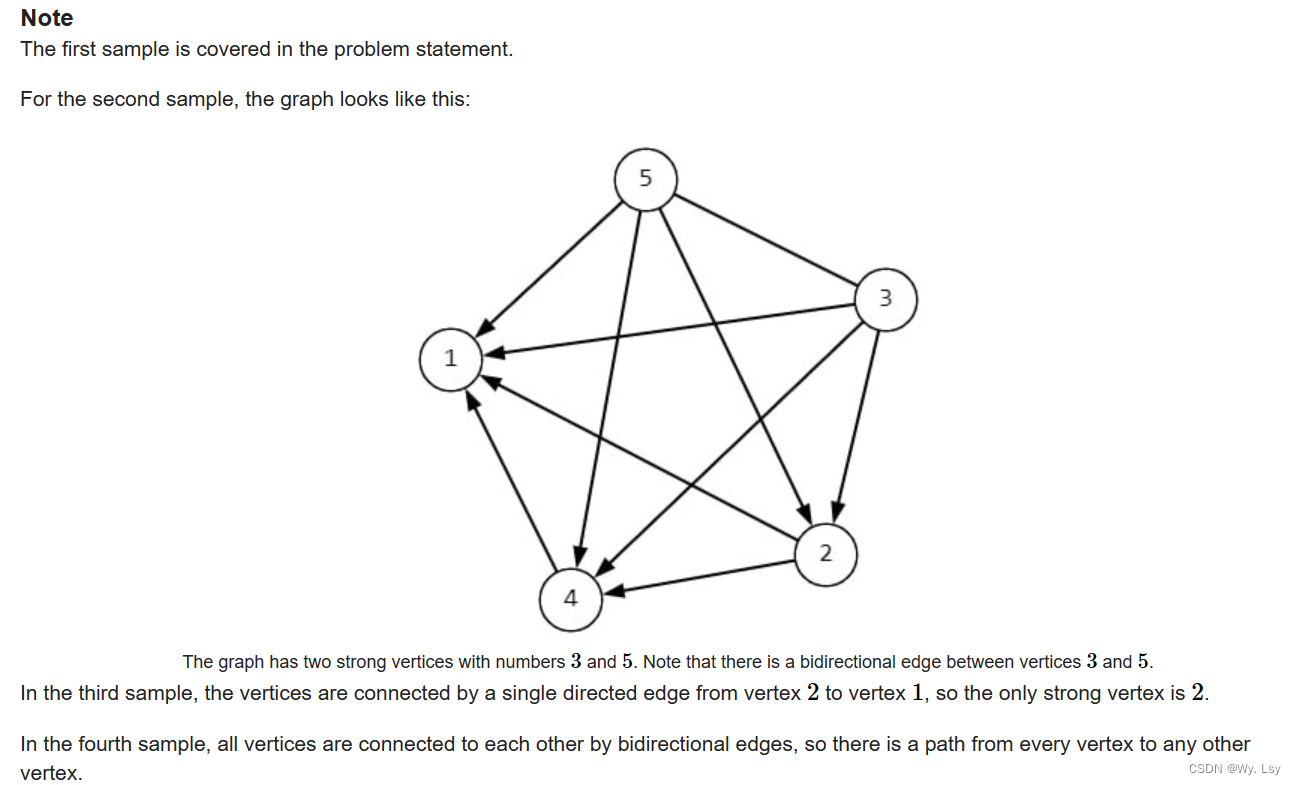
D. Strong Vertices - 思维 + 二分
分析: 首先找到边的指向很容易,但是暴力是o(n2),超时,可以将给定的式子变形,au - av > bu - bv即au - bu > av - bv,可以将两个数组转变为一个数组中的任意两个值之间的关系,因…...

8月9日上课内容 nginx负载均衡
负载均衡工作当中用的很多的,也是面试会问的很重要的一个点 负载均衡:通过反向代理来实现(nginx只有反向代理才能做负载均衡) 正向代理的配置方法(用的较少) 反向代理的方式:四层代理与七层代…...

为何我们都应关心算法备案?
随着技术的日新月异,算法成为现代生活的核心组成部分,从社交媒体推荐、在线广告到智能交通管理,几乎无处不在。然而,如此普及的技术给我们带来了一个新的挑战:如何确保算法的透明度、公正性和道德性?答案可…...
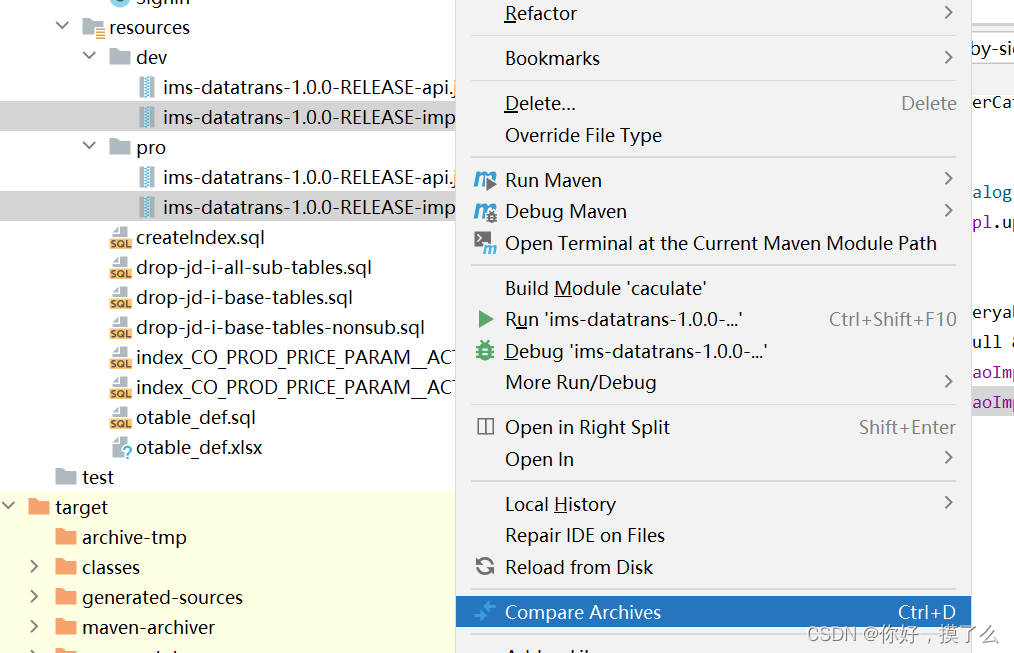
[IDEA]使用idea比较两个jar包的差异
除了一些小工具外,idea自带了jar包比较的功能。 把需要比对的jar包放到任意目录下,然后选中两个需要比较的jar包,右键,选择Compare Archives,然后就可以比较了。 这次疏忽了,每次打包前需要commit界面看一下…...

HTML笔记(2)
列表标签 项目标识符(项目符号)一般是不需要的 代码演示 改变符号样式,type属性 表格标签 代码演示 练习案例 布局标签 div是块儿级标签,占一整行; span标签不会占一整行,它只占包裹内容的那块儿区域&a…...

前端大屏自适应缩放
简介 前端中大屏往往用于展示各种炫酷的界面和特效,因此特别受用好欢迎。 但是在开发过程中,常常也会出现各种问题,与一般的页面相比, 最让人头疼的是大屏的自适应问题。使用CSS中transform属性和js获取缩放比例方法 先简单写一下…...

【Express.js】全面鉴权
全面鉴权 这一节我们来介绍一下 Passport.js,这是一个强大的 NodeJS 的认证中间件 Passport.js 提供了多种认证方式,账号密码、OpenID、ApiKey、JWT、OAuth、三方登录等等。 使用 Passport.js 认证要配置三个部分: 认证策略中间件会话 接…...

了解华为(H3C)网络设备和OSI模型基本概念
目录 一,认识华为 1.华为发展史 2.华为网络设备介绍 3.VRP概述 二,OSI七层模型 1.七层模型详细表格 2.各层的作用 3.数据在各层之间的传递过程 4.OSI四层网络模型 一,认识华为 官网:https://www.huawei.com/cn/ 1.华为发…...

Web3到底是个啥?
Web3是近两年来科技领域最火热的概念之一,但是目前对于Web3的定义却仍然没有形成标准答案,相当多对于Web3的理解,都是建立在虚拟货币行业(即俗称的“币圈”)的逻辑基础之上的。 区块链服务网络(BSN&#x…...

山东高校的专利申请人经常掉进的误区2
02、专利技术交底书只提供简单思路 一些高校科研人员在申请专利时,给专利代理人的技术交底书往往只给出了思路,或者技术方案不够详细,或者根本不会有实验验证过程和数据。 事实上,专利技术交底书的详尽程度将直接影响代理人对技…...

关于webpack的基本配置
文章目录 前言一、webpack基本配置1.配置拆分和merge2. 启动服务3、处理es6,配置babel4、处理样式5、处理图片 前言 为什么要有webpack构建和打包? 更好的模块化管理。webpack支持模块化规范:代码分割成独立模块,并管理模块之间…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

GruntJS-前端自动化任务运行器从入门到实战
Grunt 完全指南:从入门到实战 一、Grunt 是什么? Grunt是一个基于 Node.js 的前端自动化任务运行器,主要用于自动化执行项目开发中重复性高的任务,例如文件压缩、代码编译、语法检查、单元测试、文件合并等。通过配置简洁的任务…...
