Leetcode每日一题:2681. 英雄的力量(2023.8.1 C++)
目录
2681. 英雄的力量
题目描述:
实现代码与解析:
数学规律
原理思路:
2681. 英雄的力量
题目描述:
给你一个下标从 0 开始的整数数组 nums ,它表示英雄的能力值。如果我们选出一部分英雄,这组英雄的 力量 定义为:
i0,i1,...ik表示这组英雄在数组中的下标。那么这组英雄的力量为max(nums[i0],nums[i1] ... nums[ik])2 * min(nums[i0],nums[i1] ... nums[ik])。
请你返回所有可能的 非空 英雄组的 力量 之和。由于答案可能非常大,请你将结果对 109 + 7 取余。
示例 1:
输入:nums = [2,1,4]
输出:141
解释:
第 1 组:[2] 的力量为 2^2 * 2 = 8 。
第 2 组:[1] 的力量为 1^2 * 1 = 1 。
第 3 组:[4] 的力量为 4^2 * 4 = 64 。
第 4 组:[2,1] 的力量为 2^2 * 1 = 4 。
第 5 组:[2,4] 的力量为 4^2 * 2 = 32 。
第 6 组:[1,4] 的力量为 4^2 * 1 = 16 。
第 7 组:[2,1,4] 的力量为 4^2 * 1 = 16 。
所有英雄组的力量之和为 8 + 1 + 64 + 4 + 32 + 16 + 16 = 141 。
示例 :
输入:nums = [1,1,1]
输出:7
解释:总共有 7 个英雄组,每一组的力量都是 1 。所以所有英雄组的力量之和为 7 。
实现代码与解析:
数学规律
class Solution {
public:int mod = 1e9 + 7;int sumOfPower(vector<int>& nums) {sort(nums.begin(), nums.end());long long res = 0, sum = 0;for (int i = 0; i < nums.size(); i++){res = (res + (long long)nums[i] * (long long)nums[i] % mod * (nums[i] + sum)) % mod;sum = (sum * 2 + nums[i]) % mod; }return res;}
};原理思路:
分析题目,可以发现,其实英雄能力值之和每个子集的最大值和最小值有关,所有我们先sort排序,然后遍历,让其作为最大值,这是固定的,所以只要找出以 nums[ i ] 为最大值结尾的子集的最小值的和与最大值的平方相乘就得出了此种情况的英雄力量的和,最后全加起来,就得到了答案。
所以关键的核心就时如何求出以 nums[ i ] 为最大值结尾的子集的最小值的和。
比如排序后{1, 2, 3, 4}, 当遍历到4时,以其为最大值的子集有多少种?
当选择1为最小值时,2可选可不选,3可选可不选,这样就是2 * 2 = 4 个,4 * (4 * 4)* 1就为一组力量值。可以发现一组力量值是和元素的个数和最小值有关的。
那么我们可以总结出递推式,之间算出一个最大值平方需要乘的总和为:sum(nums[i] * 2 ^ 最小值与最大值中间的数字个数),i 从 0 到最大值下标。
这样就可以发现子集最小值总和明显是可以根据前一个的子集最小值总和算出来的。规律如下:
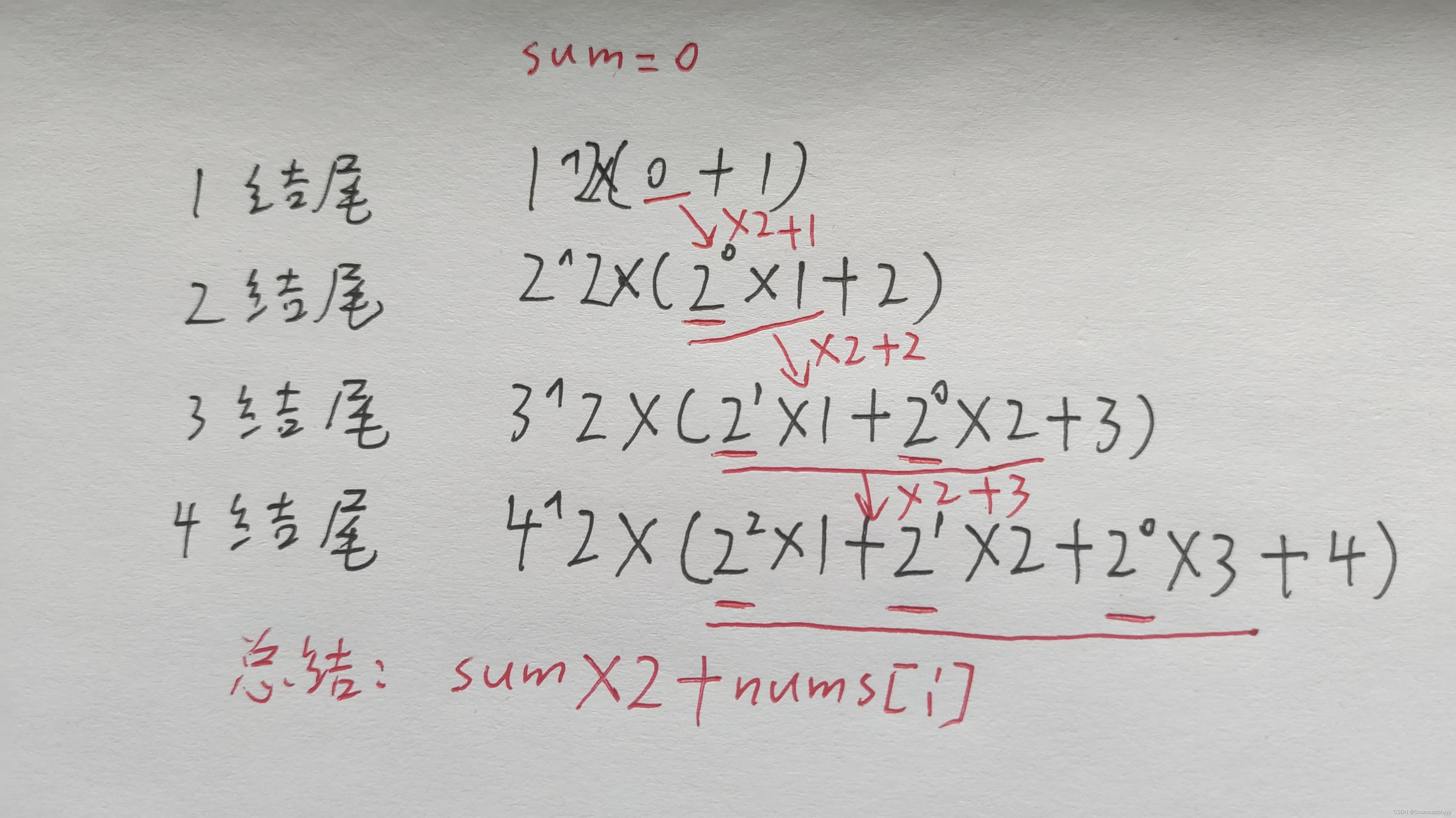
相关文章:
Leetcode每日一题:2681. 英雄的力量(2023.8.1 C++)
目录 2681. 英雄的力量 题目描述: 实现代码与解析: 数学规律 原理思路: 2681. 英雄的力量 题目描述: 给你一个下标从 0 开始的整数数组 nums ,它表示英雄的能力值。如果我们选出一部分英雄,这组英雄的…...
之 “ 异常处理”)
【学习】若依源码(前后端分离版)之 “ 异常处理”
大型纪录片:学习若依源码(前后端分离版)之 “ 异常处理” 前言1、统一返回实体定义2、定义登录异常定义3、基于ControllerAdvice注解的Controller层的全局异常统一处理4、测试访问请求结语 前言 通常一个web框架中,有大量需要处理…...
天花板级,Python接口自动化测试-接口关联封装调用(实例)
目录:导读 前言一、Python编程入门到精通二、接口自动化项目实战三、Web自动化项目实战四、App自动化项目实战五、一线大厂简历六、测试开发DevOps体系七、常用自动化测试工具八、JMeter性能测试九、总结(尾部小惊喜) 前言 流程相关的接口&a…...
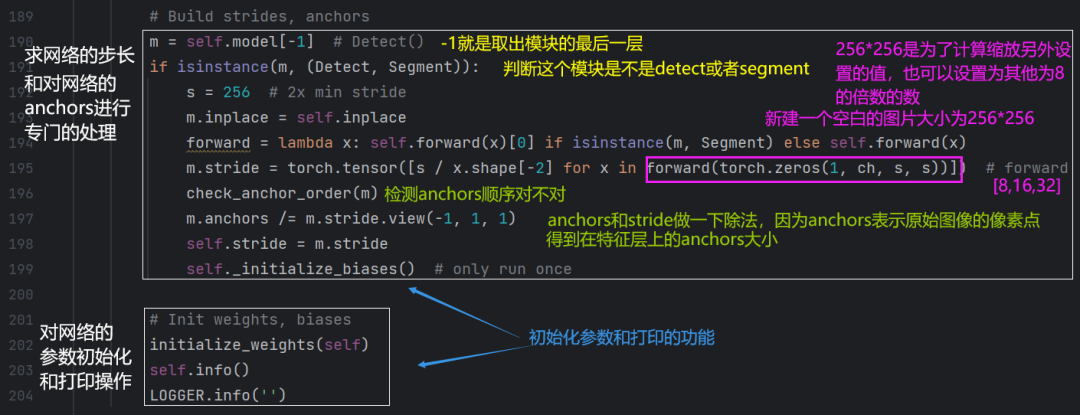
yolov5代码解读之yolo.py【网络结构】
这个文件阿对于做模型修改、模型创新有很好大好处。 首先加载一些python库和模块: 如果要执行这段代码,直接在终端输入python yolo.py. yolov5的模型定义和网络搭建都用到了model这个类(也就是以下图片展示的东西):(以前代码没…...
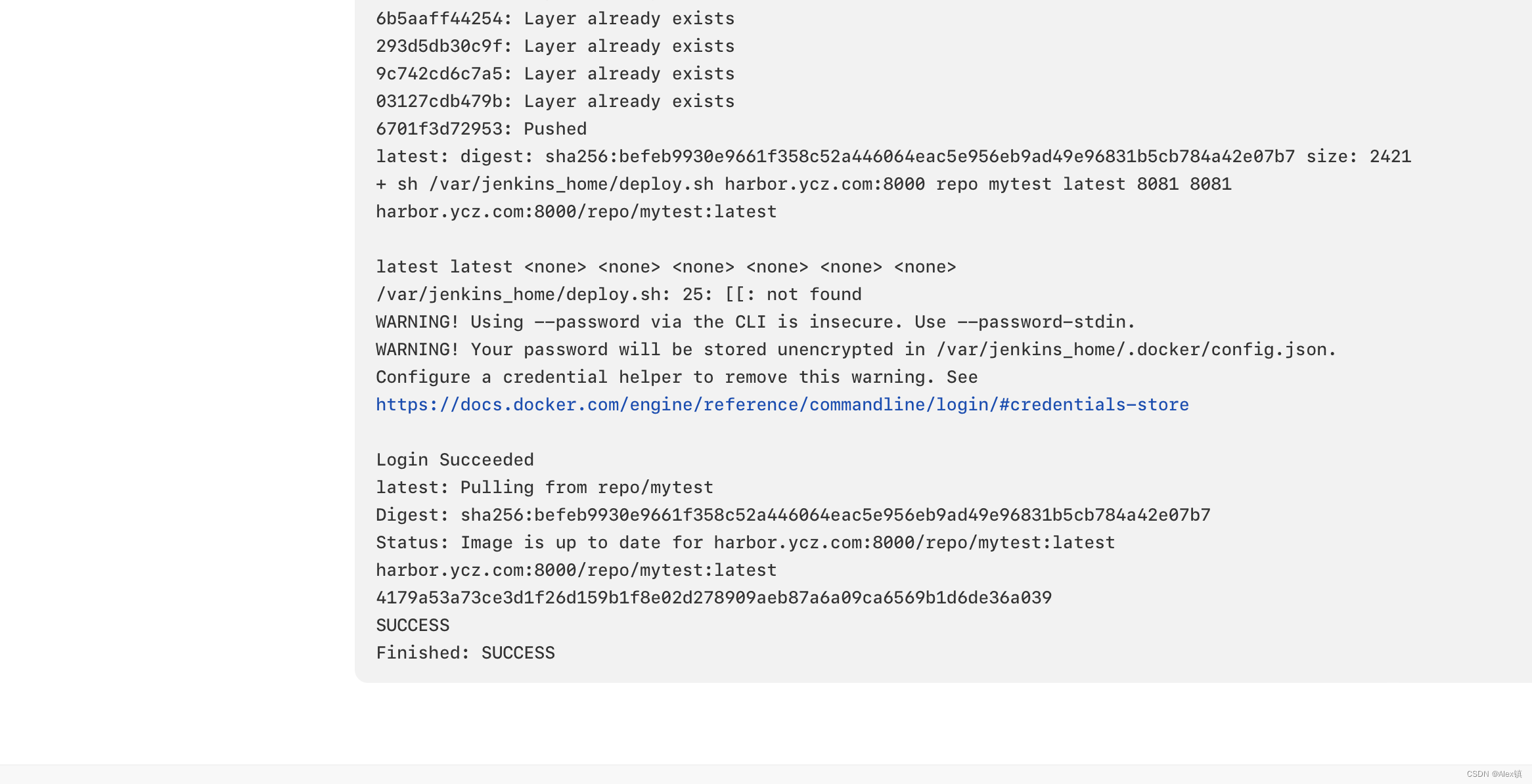
Docker之jenkins部署harbor在harbor中完成部署
Docker之jenkins部署harbor在harbor中完成部署 1、harbor作用 Harbor允许用户用命令行工具对容器镜像及其他Artifact进行推送和拉取,并提供了图形管理界面帮助用户查阅和删除这些Artifact。在Harbor 2.0版本中,除容器镜像外,Harbor对符合OCI…...
安装Jenkins
一、什么是Jenkins Jenkins是一个开源软件项目,是基于Java开发的。我们可以利用Jenkins来实现持续集成的功能。 因为Jenkins是基于Java开发的,所以在安装Jenkins之前首先需要安装Java的JDK。 二、安装Jenkins 在Windows平台上面安装Jenkins共有两种方式…...

大运空瓶行动,绘就生态文明画卷
随着成都第31届世界大学生夏季运动会赛事的成功举办,为了倡导节约水资源、绿色大运,在此之前成都电视2台《城视民生》栏目面向全市发起“大运空瓶行动”的倡议,呼吁市民杜绝水资源浪费,喝完瓶中水,并鼓励市民积极参与到…...
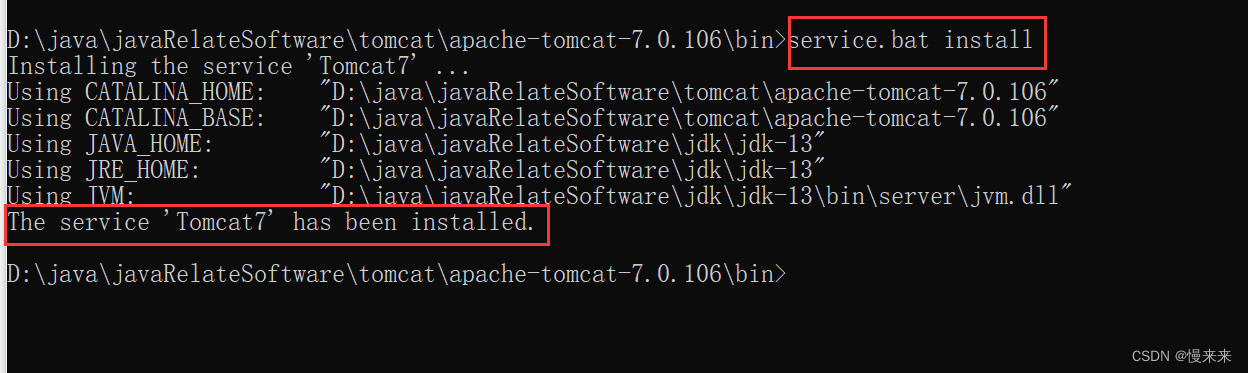
tomcat7.exe 启动闪退解决
标题tomcat7.exe 启动闪退解决 双击tomcat7.exe启动,但是出现闪退问题,无法启动tomcat 解决: 1.解决 tomcat7.exe 启动闪退解决 第一步:双击打开tomcat7w.exe 文件 如果出现 “指定的服务未安装。 Unable to open the service ‘…...

java修改jar包中的配置文件
方法一 !!!除了以上的方式,其实也可以通过 vim 命令直接修改 jar 包配置文件的内容,然后直接保存即可,不过这种方法必须保证服务器上已经安装了 zip 和 unzip 命令。 方法二 首先需要找出你的配置文件在…...
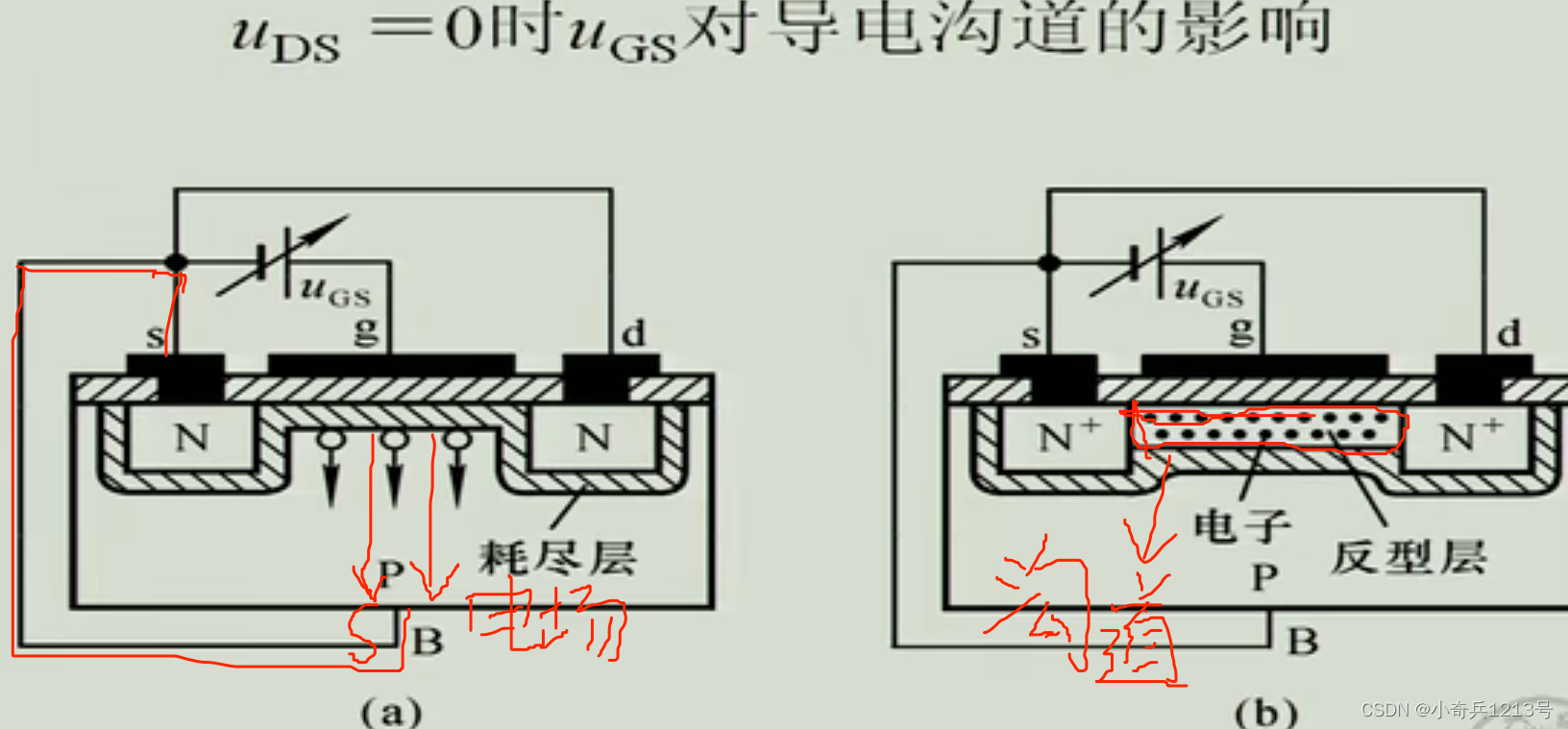
半导体器件||的学习
电子管的介绍: 到底什么是电子管(真空管)? - 知乎 芯片破壁者(一):从电子管到晶体管“奇迹”寻踪 - 知乎 晶体管: 什么是晶体管?它有什么作用? - 知乎 改…...
jenkins流水线
1.拉取代码 https://gitee.com/Wjc_project/yygh-parent.git2、项目编译 mvn clean package -Dmaven.test.skiptrue ls hospital-manage/target3、构建镜像 ls hospital-manage/target docker build -t hospital-manage:latest -f hospital-manage/Dockerfile ./hospital-ma…...
视频监控汇聚EasyCVR平台WebRTC流地址无法播放的原因排查
开源EasyDarwin视频监控TSINGSEE青犀视频平台EasyCVR能在复杂的网络环境中,将分散的各类视频资源进行统一汇聚、整合、集中管理,在视频监控播放上,TSINGSEE青犀视频安防监控汇聚平台可支持1、4、9、16个画面窗口播放,可同时播放多…...
NOSQL——redis的安装,配置与简单操作
目录 一、缓存的相关知识 1)缓存的概念 2)系统缓存 buffer与cache: 3)缓存保存位置及分层结构 DNS缓存 应用层缓存 数据层缓存 分布式缓存服务: 数据库: 硬件缓存 二、关系型数据与非关系型数据…...
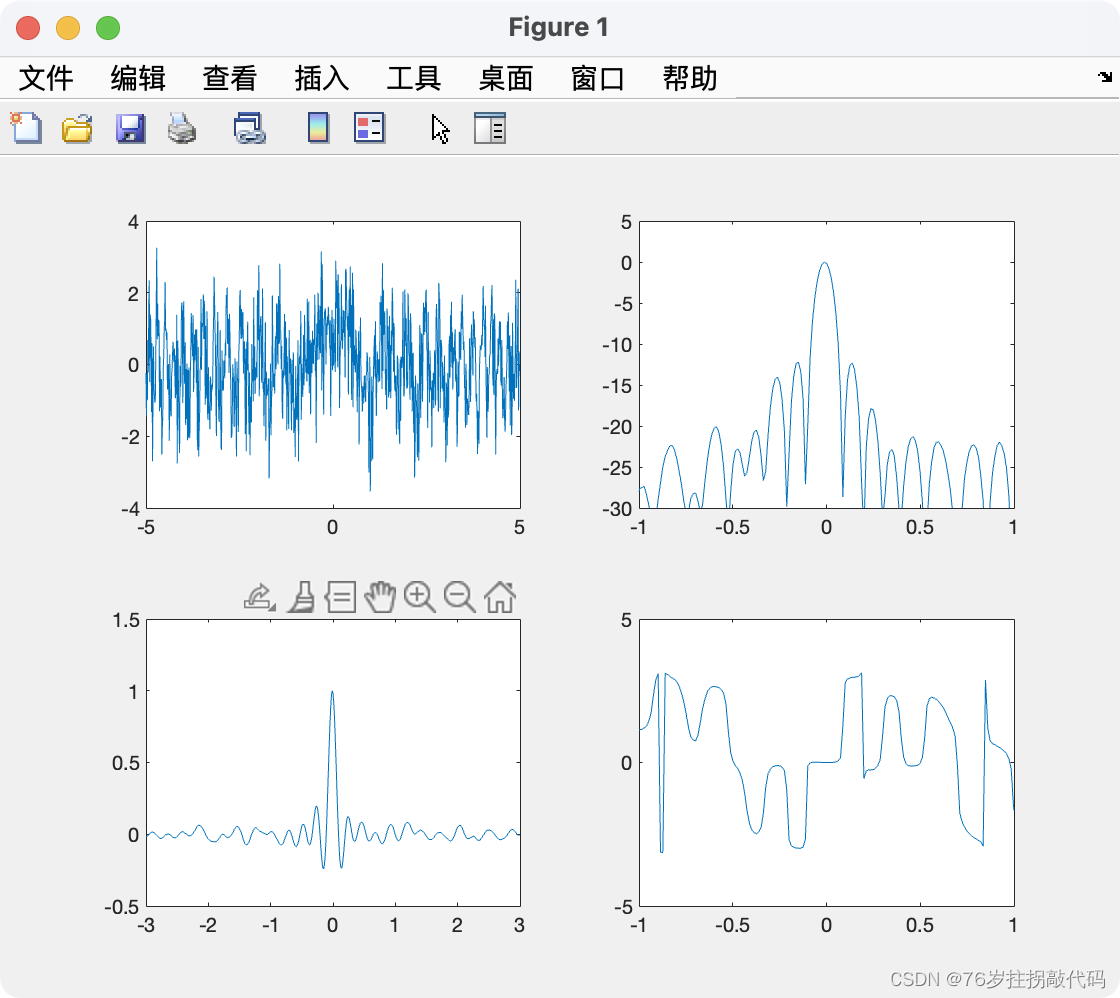
《合成孔径雷达成像算法与实现》Figure3.7
代码复现如下: clc clear all close all%参数设置 TBP 100; %时间带宽积 T 10e-6; %脉冲持续时间%参数计算 B TBP/T; …...
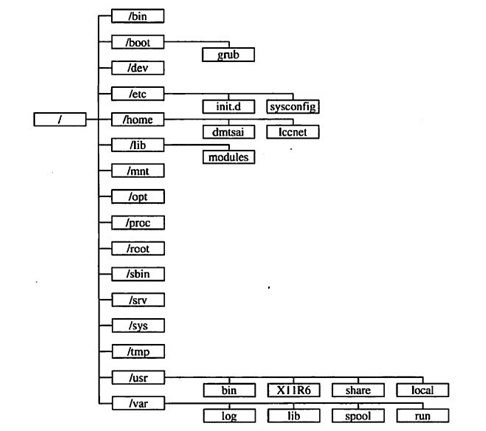
Linux 目录结构
初学Linux,首先需要弄清Linux 标准目录结构 / root --- 启动Linux时使用的一些核心文件。如操作系统内核、引导程序Grub等。home --- 存储普通用户的个人文件 ftp --- 用户所有服务httpdsambauser1user2bin --- 系统启动时需要的执行文件(二进制&#x…...

7天获英国名校邀请函|CSC青骨获批成功案例补记
Q老师要求2周内拿到邀请函且必须是世界排名前200名的高校。我们在第7天就获得了世界百强名校-英国兰卡斯特大学的邀请函,导师的研究方向完全契合,提前实现了Q老师的委托目标,使其顺利获批CSC青骨项目。特别提示:青骨项目国内派出院…...

ffmpeg ts列表合并为mp4
操作系统:ubuntu 注意事项: 1.ts文件顺序必须正确,也就是下一帧的dst和pst要比上一帧的大,否则会报错 2.codecpar->codec_tag要设置为0,否则报错Tag [27][0][0][0] incompatible with output codec id ‘27’ (avc1…...

MATLAB程序初始化OpenFOAM颗粒位置
问题引入 在OpenFOAM的颗粒两相流求解器中,我们可以采用manualInjection的方式进行自定义颗粒的初始位置,这个命令十分方便,在CFDEM中也有类似的命令,不过CFDEM中的命令更加强大,我们不仅可以定义颗粒的初始位置&…...

软件第三方CMA、CNAS测试的目的和意义,信息化建设验收测试依据是什么?
在当今互联网时代,软件的第三方CMA、CNAS测试成为了软件行业的重要环节。那么,这个测试的目的和意义是什么呢?另外,信息化建设验收测试依据又是什么呢? 一、软件测试第三方CMA、CNAS测试的目的和意义 1、研究进展 随着软件行业的迅…...
CNN成长路:从AlexNet到EfficientNet(02)
一、说明 在~10年的深度学习中,进步是多么迅速!早在 2012 年,Alexnet 在 ImageNet 上的准确率就达到了 63.3% 的 Top-1。现在,我们超过90%的EfficientNet架构和师生训练(teacher-student)。 二、第一阶段 …...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...

CSS | transition 和 transform的用处和区别
省流总结: transform用于变换/变形,transition是动画控制器 transform 用来对元素进行变形,常见的操作如下,它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...
