(贪心) 剑指 Offer 14- I. 剪绳子 ——【Leetcode每日一题】
❓剑指 Offer 14- I. 剪绳子
难度:中等
给你一根长度为 n 的绳子,请把绳子剪成整数长度的 m 段(m、n都是整数,n > 1 并且 m > 1),每段绳子的长度记为 k[0],k[1]...k[m-1] 。请问 k[0]*k[1]*...*k[m-1] 可能的最大乘积是多少?例如,当绳子的长度是8时,我们把它剪成长度分别为2、3、3的三段,此时得到的最大乘积是18。
示例 1:
输入: 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1
示例 2:
输入: 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36
提示:
2 <= n <= 58
注意:本题与 343. 整数拆分 相同。
💡思路:贪心
尽可能得多剪长度为 3 的绳子,并且不允许有长度为 1 的绳子出现。
(如果出现了,就从已经切好长度为 3 的绳子中拿出一段与长度为 1 的绳子重新组合,把它们切成两段长度为 2 的绳子。)以下为证明过程:
- 将绳子拆成
1和n-1,则1(n-1) - n = -1 < 0,即拆开后的乘积一定更小,所以不能出现长度为 1 的绳子。 - 将绳子拆成
2和n-2,则2(n-2) - n = n - 4,在n >= 4时这样拆开能得到的乘积会比不拆更大。 - 将绳子拆成
3和n-3,则3(n-3) - n = 2n - 9,在n >= 5时效果更好。 - 将绳子拆成
4和n-4,因为4=2 * 2,因此效果和拆成2一样。 - 将绳子拆成
5和n-5,因为5=2+3,而5<2*3,所以不能出现5的绳子,而是尽可能拆成2和3。 - 将绳子拆成
6和n-6,因为6=3+3,而6<3*3,所以不能出现6的绳子,而是拆成3和3。这里6同样可以拆成6=2+2+2,但是3(n - 3) - 2(n - 2) = n - 5 >= 0,在n>=5的情况下将绳子拆成3比拆成2效果更好。 ...
继续拆成更大的绳子可以发现都比拆成 2 和 3 的效果更差,因此我们只考虑将绳子拆成 2 和 3,并且优先拆成 3,当拆到绳子长度 n 等于 4 时,也就是出现 3+1,此时只能拆成 2+2。
🍁代码:(C++、Java)
C++
class Solution {
public:int cuttingRope(int n) {if(n == 2) return 1;if(n == 3) return 2;if(n == 4) return 4;int ans = 1;while(n >= 5){ans *= 3;n -= 3;}return ans * n;}
};
Java
class Solution {public int cuttingRope(int n) {if(n == 2) return 1;if(n == 3) return 2;if(n == 4) return 4;int ans = 1;while(n >= 5){ans *= 3;n -= 3;}return ans * n;}
}
🚀 运行结果:

🕔 复杂度分析:
- 时间复杂度: O ( l o g 3 n ) O(log3n) O(log3n)。
- 空间复杂度: O ( 1 ) O(1) O(1),只需要使用常数复杂度的额外空间。
题目来源:力扣。
放弃一件事很容易,每天能坚持一件事一定很酷,一起每日一题吧!
关注我LeetCode主页 / CSDN—力扣专栏,每日更新!
注: 如有不足,欢迎指正!
相关文章:

(贪心) 剑指 Offer 14- I. 剪绳子 ——【Leetcode每日一题】
❓剑指 Offer 14- I. 剪绳子 难度:中等 给你一根长度为 n 的绳子,请把绳子剪成整数长度的 m 段(m、n都是整数,n > 1 并且 m > 1),每段绳子的长度记为 k[0],k[1]...k[m-1] 。请问 k[0]*k[1]*...*k[m…...
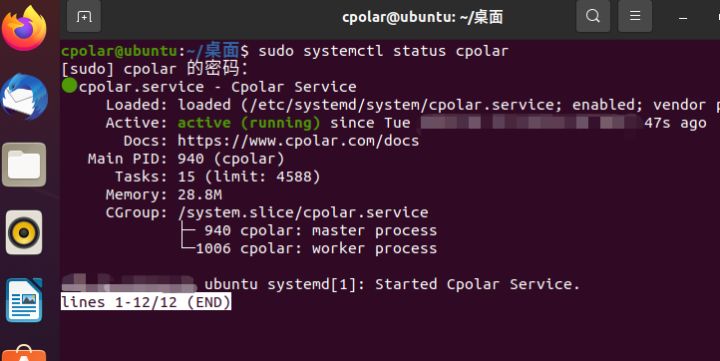
如何将Linux上的cpolar内网穿透设置成 - > 开机自启动
如何将Linux上的cpolar内网穿透设置成 - > 开机自启动 文章目录 如何将Linux上的cpolar内网穿透设置成 - > 开机自启动前言一、进入命令行模式二、输入token码三、输入内网穿透命令 前言 我们将cpolar安装到了Ubuntu系统上,并通过web-UI界面对cpolar的功能有…...
)
50.两数之和(力扣)
目录 问题描述 核心代码解决 代码思想 时间复杂度和空间复杂度 问题描述 给定一个整数数组 和一个整数目标值 ,请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。numstarget 你可以假设每种输入只会对应一个答案。但是&am…...
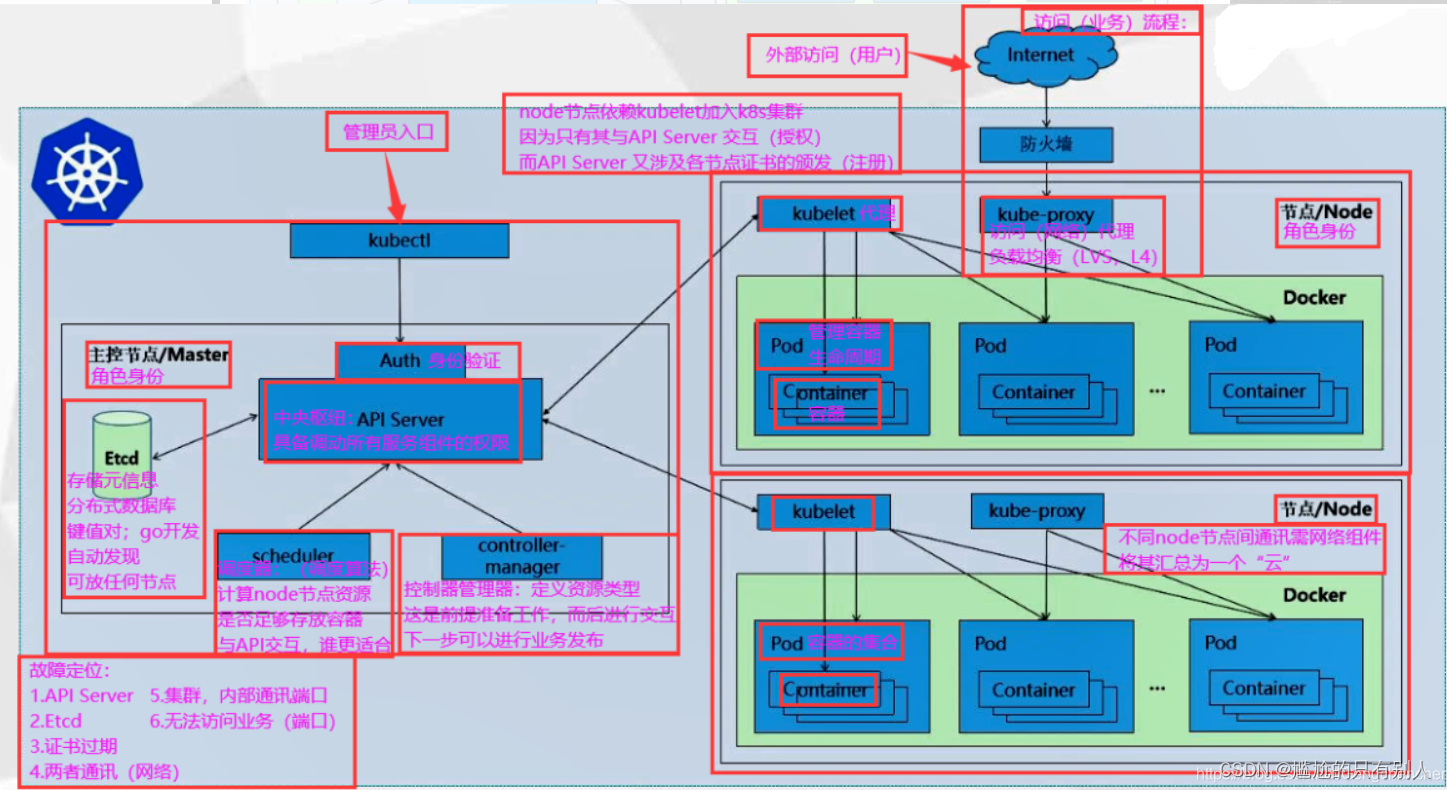
k8s基础
k8s基础 文章目录 k8s基础一、k8s组件二、k8s组件作用1.master节点2.worker node节点 三、K8S创建Pod的工作流程?四、K8S资源对象1.Pod2.Pod控制器3.service && ingress 五、K8S资源配置信息六、K8s部署1.K8S二进制部署2.K8S kubeadm搭建 七、K8s网络八、K8…...

【自然语言处理】大模型高效微调:PEFT 使用案例
文章目录 一、PEFT介绍二、PEFT 使用2.1 PeftConfig2.2 PeftModel2.3 保存和加载模型 三、PEFT支持任务3.1 Models support matrix3.1.1 Causal Language Modeling3.1.2 Conditional Generation3.1.3 Sequence Classification3.1.4 Token Classification3.1.5 Text-to-Image Ge…...
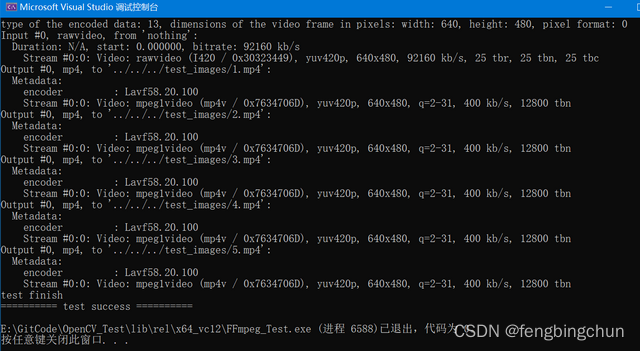
FFmpeg将编码后数据保存成mp4
以下测试代码实现的功能是:持续从内存块中获取原始数据,然后依次进行解码、编码、最后保存成mp4视频文件。 可保存成单个视频文件,也可指定每个视频文件的总帧数,保存多个视频文件。 为了便于查看和修改,这里将可独立的…...

设置VsCode 将打开的多个文件分行(栏)排列,实现全部显示
目录 1. 前言 2. 设置VsCode 多文件分行(栏)排列显示 1. 前言 主流编程IDE几乎都有排列切换选择所要查看的文件功能,如下为Visual Studio 2022的该功能界面: 图 1 图 2 当在Visual Studio 2022打开很多文件时,可以按照图1、图2所示找到自…...

Vue.js2+Cesium1.103.0 六、标绘与测量
Vue.js2Cesium1.103.0 六、标绘与测量 点,线,面的绘制,可实时编辑图形,点击折线或多边形边的中心点,可进行添加线段移动顶点位置等操作,并同时计算出点的经纬度,折线的距离和多边形的面积。 De…...

【redis 延时队列】使用go-redis的list做异步,生产消费者模式
分享一个用到的,使用go-redis的list做异步,生产消费者模式,接着再用 go 协程去检测队列里是否有东西去消费 如果队列为空,就会一直pop,空轮询导致 cpu 资源浪费和redis qps无效升高,所以可以通过 time.Sec…...
激光焊接塑料多点测试全画面穿透率测试仪
工程塑料由于其具有高比强度、电绝缘性、耐磨性、耐腐蚀性等优点,已广泛应用于各个重要领域。另一方面,工程塑料还具有良好的焊接性,是制成复合材料的基体材料的优良选择,因此目前已成为国内外新型复合材料的研究热点。 工程塑料…...

用 Uno 当烧录器给 atmega328 烧录 bootloader
用 Uno 当烧录器给 atmega328 烧录 bootloader date: 2023-8-10 https://backmountaindevil.github.io/#/hackaday/arduino/isp 引脚接线 把两个板子的 11(MOSI)、12(MISO)、13(SCK)、5V、GND 两两相连,还要把 Uno(烧录器)的 10 接到atmeg…...
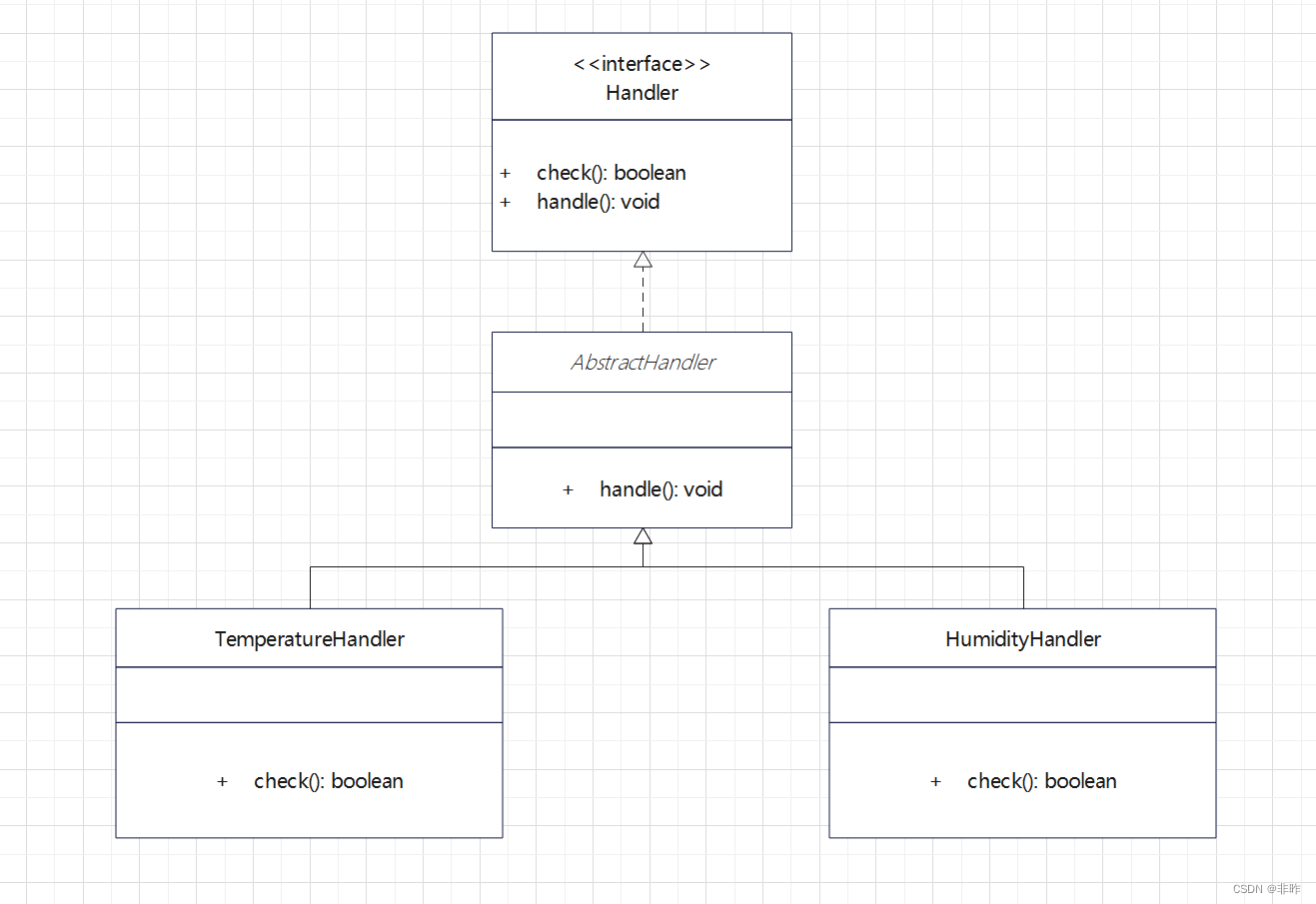
spring boot策略模式实用: 告警模块为例
spring boot策略模式实用: 告警模块 0 涉及知识点 策略模式, 模板方法, 代理, 多态, 反射 1 需求概括 场景: 每隔一段时间, 会获取设备运行数据, 如通过温湿度计获取到当前环境温湿度;需求: 对获取回来的进行分析, 超过配置的阈值需要产生对应的告警 2 方案设计 告警的类…...

Camunda 7.x 系列【10】使用 Rest API 运行流程实例
有道无术,术尚可求,有术无道,止于术。 本系列Spring Boot 版本 2.7.9 本系列Camunda 版本 7.19.0 源码地址:https://gitee.com/pearl-organization/camunda-study-demo 文章目录 1. 前言2. 官方接口文档3. 本地接口文档3.1 Postman3.2 Camunda Platform Run Swagger3.3 S…...

Python-OpenCV中的图像处理-边缘检测
Python-OpenCV中的图像处理-边缘检测 边缘检测Canny算子 边缘检测Canny算子 Canny 边缘检测是一种非常流行的边缘检测算法,是 John F.Canny 在 1986 年提出的。它是一个有很多步构成的算法:噪声去除、计算图像梯度、非极大值抑制、滞后阀值等。 Canny(i…...
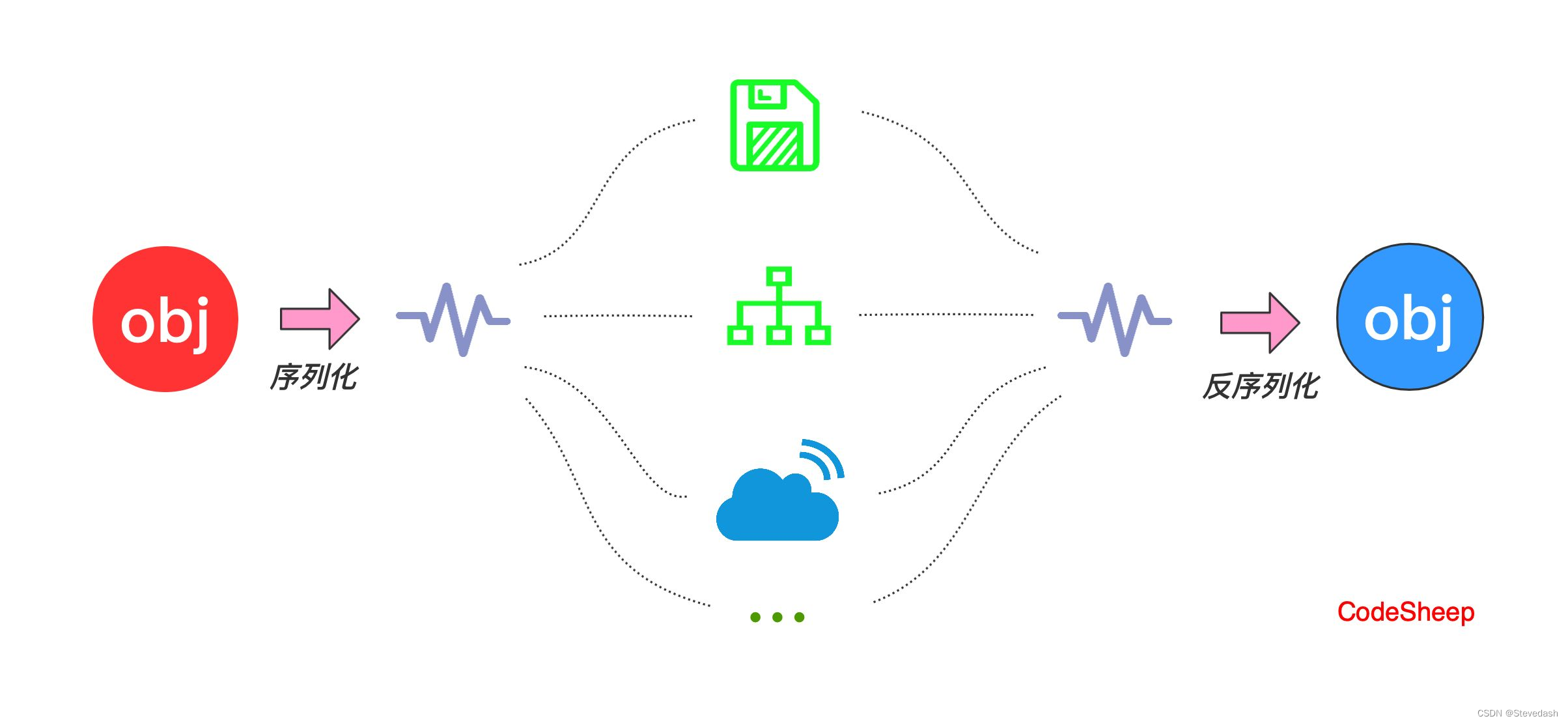
一文了解Java序列化和反序列化:对象的存储与传输
一文了解Java序列化和反序列化:对象的存储与传输 作者:Stevedash 发布时间:2023年8月9日 21点30分 前言 Java序列化是一项强大而重要的技术,它允许我们将对象转换为字节流,以便在存储、传输和重建时使用。在本文中&…...

react-codemirror2 编辑器需点击一下或者延时才显示数据的问题
现象: <Codemirror/>组件的数据已经赋上值的情况下,初始状态不渲染数据,需要点击编辑框获取焦点后才展示,或者延迟了几秒才显示出来。 原因: 指定了一些依赖的版本,可能不兼容了一些功能,…...
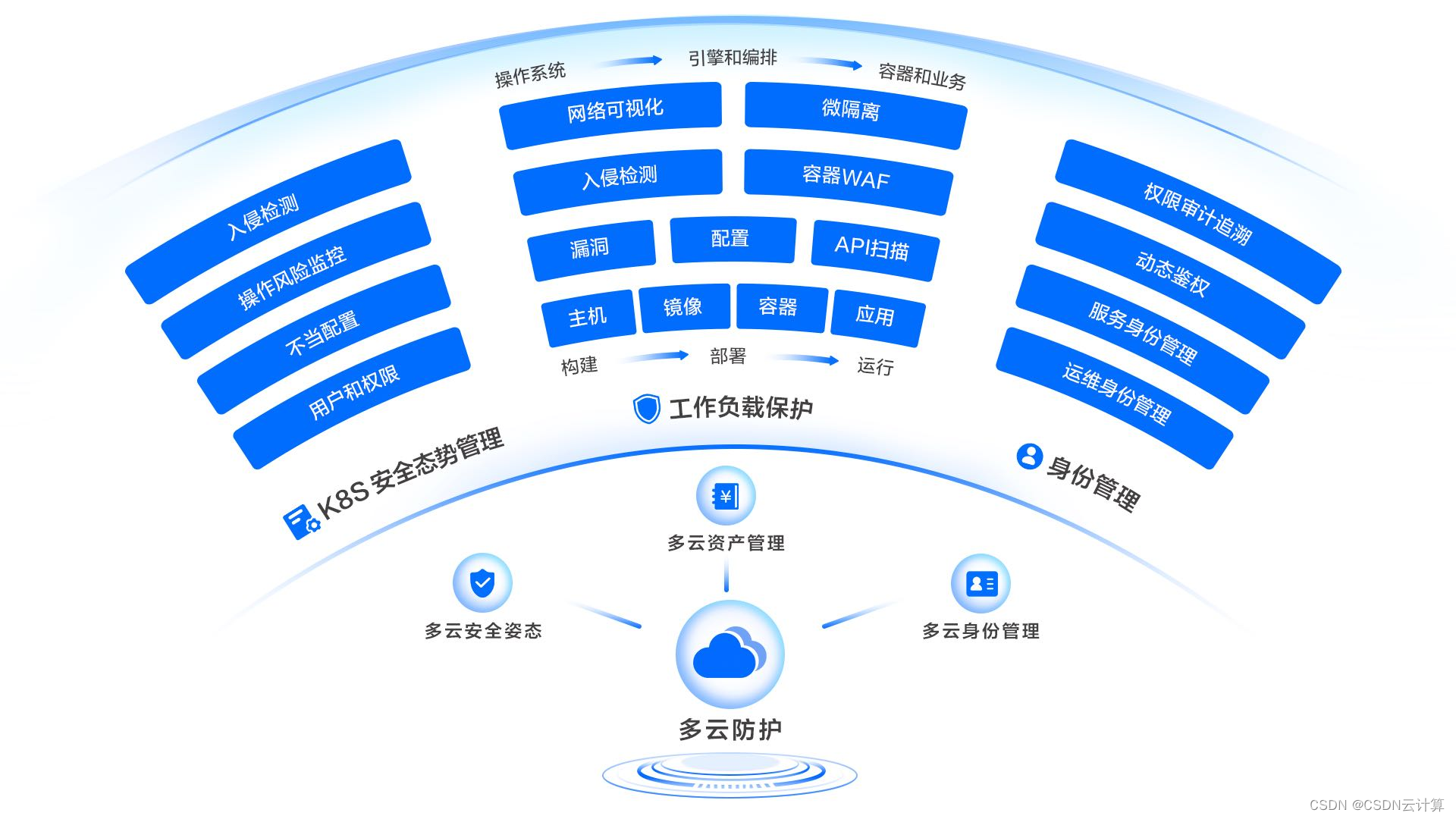
火山引擎联合Forrester发布《中国云原生安全市场现状及趋势白皮书》,赋能企业构建云原生安全体系
国际权威研究咨询公司Forrester 预测,2023年全球超过40%的企业将会采用云原生优先战略。然而,云原生在改变企业上云及构建新一代基础设施的同时,也带来了一系列的新问题,针对涵盖云原生应用、容器、镜像、编排系统平台以及基础设施…...

需要数电发票接口的,先熟悉下数电发票基本常识
最近有一些技术小伙伴来咨询数电发票接口的时候,对数电发票的一些常识不太了解, 导致沟通起来比较困难。比较典型的这三个问题: 一、开具数电票时,如何设置身份认证频次? 请公司的法定代表人或财务负责人登录江苏省电…...

node-sass是什么
一、Sass(Syntactically Awesome Style Sheets) 是一种CSS预处理器,它扩展了CSS的功能并提供了更强大的样式表语言。Sass允许开发人员使用变量、嵌套规则、混合(Mixins)、继承等高级功能来编写更简洁、可维护的样式代…...

C语言指针之 进阶
前言 今天来较为深入的介绍一下指针,希望大家能有所收获~ 那么,先进行一些简单的基础知识复习吧。 字符指针 格式:char * 补充: 表达式“abcdef”的值是首字符a的地址 所以当像下面这么使用时,它的含…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...

jmeter聚合报告中参数详解
sample、average、min、max、90%line、95%line,99%line、Error错误率、吞吐量Thoughput、KB/sec每秒传输的数据量 sample(样本数) 表示测试中发送的请求数量,即测试执行了多少次请求。 单位,以个或者次数表示。 示例:…...
