算法的时间复杂度
算法在编写成可执行程序后,运行时需要消耗时间资源和空间(内存)资源,因此衡量一个算法的好坏,一般是从时间和空间两个维度来衡量的。
时间复杂度主要衡量一个算法运行的快慢,而空间复杂度主要衡量一个算法运行所需要的额外空间,今天我们主要来讲讲时间复杂度。
目录
一、时间复杂度的概念
二、大O的渐进表示法
三、常见的时间复杂度计算
一、时间复杂度的概念
一个算法所花的时间与其中语句的执行次数成正比,算法中的基本操作的执行次数,为算法的时间复杂度。
二、大O的渐进表示法
实际计算时间复杂度时,我们并不需要计算精确的执行次数,而只需要大概执行次数,那么这里我们使用大O的渐进表示法。
大O符号:是用于描述函数渐进行为的数学符号。
推导大O阶的方法:
1、用常数1取代运行时间中所有的加法常数。
2、在修改后的运行次数函数中,只保留最高阶项。
3、如果最高阶项存在且不是1,则去除与这个项相乘的常数,得到的结果就是大O阶。
另外,有些算法的时间复杂度存在最好、平均、最坏的情况。
最坏情况:
任意输入规模的最大运行次数(上线)
平均情况:
任意输入规模的期望运行次数
最好情况:
任意输入规模的最小运行次数
例如,在一个长度为N的数组中搜索一个数据x
最好情况:一次找到
平均情况:N/2次找到
最坏情况:N次找到
在实际中一般情况关注的是算法的最坏运行情况,所以数组中搜索数据时间复杂度为O(N)
三、常见的时间复杂度计算
实例1:
void BubbleSort(int *a,int n)
{assert(a);for(size_t end=n;end>0;--end){int exchange = 0;for(size_t i=1;i<end;++i){if(a[i-1]>a[i]){Swap(&a[i-1],&a[i]);exchange=1;}}if(exchange=0)break;}
}
该例子为冒泡排序,最好的情况为,比较完一轮(N-1次)后,发现就顺序的,所以最好是N次。
最坏是(N*(N+1))/2次,通过推导大O阶方法+时间复杂度一般看最坏,时间复杂度为O(N^2).
实例2:
//二分查找
int BinarySearch(int* a, int n, int x)
{assert(a);int begin = 0;int end = n - 1;while (begin <= end){int mid = begin + ((end - begin) >> 1);if (a[mid] < x){begin = mid + 1;}else if(a[mid]>x){end = mid - 1;}else{return mid;}}return -1;
}二分查找:
最好情况:中间那个数就是要找的O(1)
最坏情况:一直除2,,到只剩一个值时,要么找到了,要么找不到。
假设N是数组个数,x是最坏查找次数,N/2/2/2……/2=1
2^x=N,x=logN(logN在算法分析中表示以2为底数,N为对数,有些地方也写成lg N)
实例3:
//计算斐波那契数列的时间复杂度
long long Fib(size_t N)
{if (N < 3)return 1;return Fib(N - 1) + Fib(N - 2);
}
运用等比数列求和公式可知,执行次数为2^N的数量级
所以时间复杂度应为O(2^N)
实例4:
//计算阶乘递归Fac的时间复杂度
long long Fac(size_t N)
{if (0 == N)return 1;return Fac(N - 1) * N;
}时间复杂度为O(N)
相关文章:

算法的时间复杂度
算法在编写成可执行程序后,运行时需要消耗时间资源和空间(内存)资源,因此衡量一个算法的好坏,一般是从时间和空间两个维度来衡量的。 时间复杂度主要衡量一个算法运行的快慢,而空间复杂度主要衡量一个算法运…...
 | 机试题算法思路 【2023】)
华为OD机试 - 叠放书籍(Python) | 机试题算法思路 【2023】
最近更新的博客 华为OD机试 - 寻找路径 | 备考思路,刷题要点,答疑 【新解法】 华为OD机试 - 五键键盘 | 备考思路,刷题要点,答疑 【新解法】 华为OD机试 - IPv4 地址转换成整数 | 备考思路,刷题要点,答疑 【新解法】 华为OD机试 - 对称美学 | 备考思路,刷题要点,答疑 …...
进程间通信(重点)
概念 进程是一个独立的资源分配单元,不同进程之间的资源是独立的进程并非孤立的,不同进程需要进行信息的交互和状态的传递,因此需要进程之间的通信【IPC: Inter processes communication】 如qq聊天,qq在每个人的手机上是独立的…...
Reverse入门[不断记录]
文章目录前言一、[SWPUCTF 2021 新生赛]re1二、[SWPUCTF 2021 新生赛]re2三、[GFCTF 2021]wordy[花指令]四、[NSSRound#3 Team]jump_by_jump[花指令]五、[NSSRound#3 Team]jump_by_jump_revenge[花指令]前言 心血来潮,想接触点Reverse,感受下Reverse&am…...
如何实现外网访问内网ip?公网端口映射或内网映射来解决
本地搭建服务器应用,在局域网内可以访问,但在外网不能访问。如何实现外网访问内网ip?主要有两种方案:路由器端口映射和快解析内网映射。根据自己本地网络环境,结合是否有公网IP,是否有路由权限,…...

[acwing周赛复盘] 第 91 场周赛20230218
[acwing周赛复盘] 第 91 场周赛20230218 一、本周周赛总结二、 4861. 构造数列1. 题目描述2. 思路分析3. 代码实现三、4862. 浇花1. 题目描述2. 思路分析3. 代码实现四、4863. 构造新矩阵1. 题目描述2. 思路分析3. 代码实现六、参考链接一、本周周赛总结 这周挺难的。T1 贪心分…...

蓝桥12届
小蓝准备用 256MB 的内存空间开一个数组,数组的每个元素都是 32 位 二进制整数,如果不考虑程序占用的空间和维护内存需要的辅助空间,请问 256MB 的空间可以存储多少个 32 位二进制整数?1MB 1024KB 1KB 1024字节(byte) 1字节 8位…...
)
华为OD机试 - 斗地主(JS)
斗地主 题目 斗地主起源于湖北十堰房县, 据传是一位叫吴修全的年轻人根据当地流行的扑克玩法“跑得快”改编的, 如今已风靡整个中国,并流行于互联网上 牌型: 单顺,又称顺子,最少5张牌,最多12张牌(3...A),不能有2, 也不能有大小王,不计花色 例如:3-4-5-7-8,7-8-9-1…...

【MyBatis】| MyBatis的注解式开发
目录 一:MyBatis的注解式开发 1. Insert注解 2. Delete注解 3. Update注解 4. Select注解 5. Results注解 一:MyBatis的注解式开发 MyBatis中也提供了注解式开发⽅式,采⽤注解可以减少Sql映射⽂件的配置。 当然,使⽤注…...
python自制PDF转换.PNG格式图片(按每页生成图片完整源码)小工具!
使用PyQt5应用程序制作PDF转换成图片的小工具,可以导入PDF文档后一键生成对应的PNG图片。 PDF图片转换小工具使用的中间件: python版本:3.6.8 UI应用版本:PyQt5 PDF文件操作非标准库:PyPDF2 PNG图片生成库࿱…...

Go 数组和切片反思
切片的底层数据结构是数组,所以,切片是基于数组的上层封装,使用数组的场景,也完全可以使用切片。 类型比较 我看到 go 1.17 有对切片和数组转换的优化,禁不住纳闷,有什么场景是必须数组来完成的呢&#x…...
win10电脑性能优化设置
win10电脑性能优化设置 目录win10电脑性能优化设置1.桌面图标显示2.wini2.1 “系统”2.1.1专注助手 关2.1.2 电源和睡眠 设置为从不2.1.3 存储 开2.2 网络和Internet2.3 个性化2.4 应用2.5 账户2.6 游戏2.7 隐私墨迹书写和键入个性化:关活动历史记录:全部…...

作为初学者必须要了解的几种常用数据库!
现在已经存在了很多优秀的商业数据库,如甲骨文(Oracle)公司的 Oracle 数据库、IBM 公司的 DB2 数据库、微软公司的 SQL Server 数据库和 Access 数据库。同时,还有很多优秀的开源数据库,如 MySQL 数据库,Po…...

小红书日常实习一面面经
时间:2月13下午 平台:赛码网,视频面大概70分钟顺序大致是下面,讲到哪问到哪,基础知识最好要结合项目或者实际回答,没录音不完全,有错误请指正首先面试官人超级好,细心提问,耐心解答问…...
)
将Nginx 核心知识点扒了个底朝天(一)
什么是Nginx? Nginx是一个 轻量级/高性能的反向代理Web服务器,用于 HTTP、HTTPS、SMTP、POP3 和 IMAP 协议。他实现非常高效的反向代理、负载平衡,他可以处理2-3万并发连接数,官方监测能支持5万并发,现在中国使用ngin…...

SSM项目搭建保姆级教程
文章目录1、什么是SSM框架1.1、持久层1.2、业务层1.3、表现层1.4、View层1.5、SpringMVC执行流程1.6、MyBatis2、SSM实战搭建2.1、创建工程2.2、添加依赖2.3、配置spring.xml文件2.4、配置web.xml文件2.5、log4j.properties2.6、准备表2.7、实体类2.8、mapper2.9、service2.10、…...

LeetCode 350. 两个数组的交集 II
原题链接 难度:easy\color{Green}{easy}easy 题目描述 给你两个整数数组 nums1nums1nums1 和 nums2nums2nums2 ,请你以数组形式返回两数组的交集。返回结果中每个元素出现的次数,应与元素在两个数组中都出现的次数一致(如果出现…...

Python可以解码吗,解码打码是如何实现的
前言 咳咳,进来的铁汁都是抱着学习的心态进来看的吧,咱今天不讲解解码,咱来说说python如何来实现打码功能~ 这一个个进来的 都是标题党吧哈哈哈 有兴趣的可以继续看看哦 最近重温了一档综艺节目 至于叫什么 这里就不细说了 老是看着看着就…...
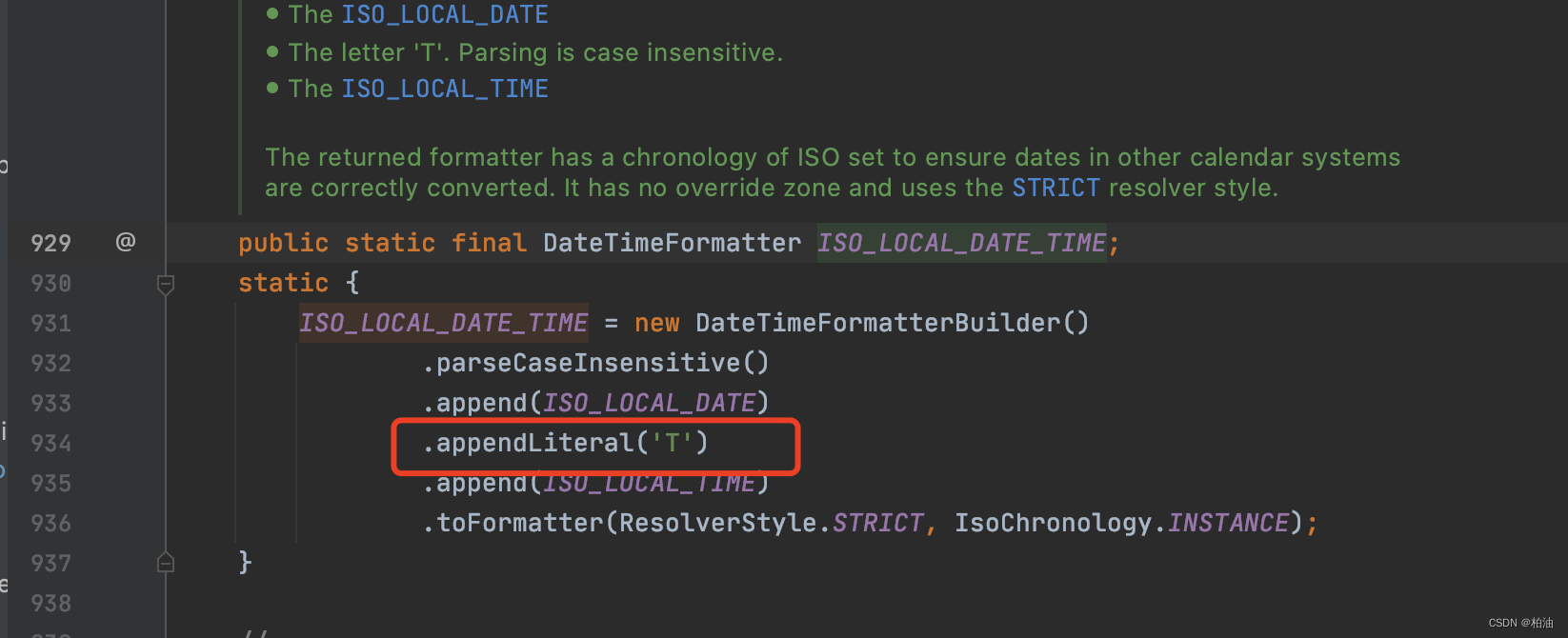
Jackson 序列化:Cannot deserialize value of type `java.time.LocalDateTime`
问题描述 使用 jackson 反序列化异常如下: Caused by: com.fasterxml.jackson.databind.exc.InvalidFormatException: Cannot deserialize value of type java.time.LocalDateTime from String “2023-02-13 19:43:01”: Failed to deserialize java.time.LocalDat…...
_习题)
机试_3_数据结构(一)_习题
数据结构(一)——练习题 学习完第三章-数据结构(一)之后,当然要做相应地练习啦~ 注:上述习题都可以在牛客进行测试。 例如,第2题链接:计算表达式_牛客题霸_牛客网 (nowcoder.com)…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

Unity中的transform.up
2025年6月8日,周日下午 在Unity中,transform.up是Transform组件的一个属性,表示游戏对象在世界空间中的“上”方向(Y轴正方向),且会随对象旋转动态变化。以下是关键点解析: 基本定义 transfor…...

webpack面试题
面试题:webpack介绍和简单使用 一、webpack(模块化打包工具)1. webpack是把项目当作一个整体,通过给定的一个主文件,webpack将从这个主文件开始找到你项目当中的所有依赖文件,使用loaders来处理它们&#x…...

从实验室到产业:IndexTTS 在六大核心场景的落地实践
一、内容创作:重构数字内容生产范式 在短视频创作领域,IndexTTS 的语音克隆技术彻底改变了配音流程。B 站 UP 主通过 5 秒参考音频即可克隆出郭老师音色,生成的 “各位吴彦祖们大家好” 语音相似度达 97%,单条视频播放量突破百万…...

简单介绍C++中 string与wstring
在C中,string和wstring是两种用于处理不同字符编码的字符串类型,分别基于char和wchar_t字符类型。以下是它们的详细说明和对比: 1. 基础定义 string 类型:std::string 字符类型:char(通常为8位)…...

OpenGL-什么是软OpenGL/软渲染/软光栅?
软OpenGL(Software OpenGL)或者软渲染指完全通过CPU模拟实现的OpenGL渲染方式(包括几何处理、光栅化、着色等),不依赖GPU硬件加速。这种模式通常性能较低,但兼容性极强,常用于不支持硬件加速…...

Centos 7 服务器部署多网站
一、准备工作 安装 Apache bash sudo yum install httpd -y sudo systemctl start httpd sudo systemctl enable httpd创建网站目录 假设部署 2 个网站,目录结构如下: bash sudo mkdir -p /var/www/site1/html sudo mkdir -p /var/www/site2/html添加测试…...
