数论 —— 高斯记号(Gauss mark)
定义
数学上,高斯记号(Gauss mark)是指对取整符号和取小符号的统称,用于数论等领域。
- 设 x∈Rx \in \textbf{R}x∈R,用 [x][x][x] 表示不超过 xxx 的最大整数。也可记作 [x][x][x]。
- 设 x∈Rx \in \textbf{R}x∈R,用 {x}\{x\}{x} 表示 xxx 的非负纯小数,即 {x}=x-[x]\{x\}=x-[x]{x}=x-[x]。
例如
- [1]=1
- [0]=0
- [-1]=-1
- [-1.2]=-2
- {1.5}=0.5
- {-1.5}=0.5
- {-1.2}=0.8
性质
- 对于任意实数 x,x=[x]+{x}
- x-1<[x]≤x<[x]+1
- [n+x]=n+[x],n 为整数
- [x]+[y]≤[x+y]≤[x]+[y]+1
例题
解方程 x+2{x}=3[x]x+2\{x\}=3[x]x+2{x}=3[x]
思路
使用定义 x=[x]+{x}
解题
根据定义 x=[x]+{x},带入原方程变为 [x]+3{x}=3[x]
2[x]=3{x}
∵0≤{x}<1\because 0≤\{x\}<1∵0≤{x}<1
∴0≤3{x}<3\therefore 0≤3\{x\}<3∴0≤3{x}<3
∵[x]\because [x]∵[x] 一定是一个整数。
∴3{x}=0,1,2\therefore 3\{x\}=0,1,2∴3{x}=0,1,2
∵2[x]\because 2[x]∵2[x] 一定是一个偶数。
∴3{x}=0,2\therefore 3\{x\}=0,2∴3{x}=0,2
带入原式进行讨论。
- 当 3{x}=03\{x\}=03{x}=0 的时候,{x}=0\{x\}=0{x}=0,对应 [x]=0[x]=0[x]=0,即 x=0x=0x=0。
- 当 3{x}=23\{x\}=23{x}=2 的时候,{x}=23\{x\}=\frac{2}{3}{x}=32,对应 [x]=1[x]=1[x]=1,即 x=53x=\frac{5}{3}x=35。
解方程 [x]{x}+x=2{x}+10[x]\{x\}+x=2\{x\}+10[x]{x}+x=2{x}+10
思路
根据性质,可得 0≤{x}<10≤\{x\}<10≤{x}<1。
我们可以将方程变成 {x}=...\{x\}=...{x}=... 形式。
解题
根据定义 x=[x]+{x},带入原方程变为 [x]{x}+[x]+{x}=2{x}+10
合并同类项
[x]{x}-{x}=10-[x]
{x}([x]-1)=10-[x]
{x}=10−[x][x]−1\{x\} = \frac{10-[x]}{[x]-1}{x}=[x]−110−[x]
∵0≤{x}<1\because 0≤\{x\}<1∵0≤{x}<1
∴0≤10−[x][x]−1<1\therefore 0≤\frac{10-[x]}{[x]-1}<1∴0≤[x]−110−[x]<1
由于分子分母都含有 [x][x][x],因此需要对分母进行配方。
10−[x][x]−1=9+1−[x][x]−1=9−([x]−1)[x]−1\frac{10-[x]}{[x]-1}=\frac{9+1-[x]}{[x]-1}=\frac{9-([x]-1)}{[x]-1}[x]−110−[x]=[x]−19+1−[x]=[x]−19−([x]−1)
0≤9−([x]−1)[x]−1<10≤\frac{9-([x]-1)}{[x]-1}<10≤[x]−19−([x]−1)<1
0≤9[x]−1−1<10≤\frac{9}{[x]-1}-1<10≤[x]−19−1<1
1≤9[x]−1<21≤\frac{9}{[x]-1}<21≤[x]−19<2
1≥[x]−19>121\ge \frac{[x]-1}{9}>\frac{1}{2}1≥9[x]−1>21
9≥[x]−1>4.59 \ge [x]-1 > 4.59≥[x]−1>4.5
10≥[x]>5.510 \ge [x] > 5.510≥[x]>5.5
∴[x]=6,7,8,9,10\therefore [x]=6,7,8,9,10∴[x]=6,7,8,9,10
带入原式进行讨论。
- 当 [x]=6[x]=6[x]=6 时候,原方程为 x=10−66−1=45{x}=\frac{10-6}{6-1}=\frac{4}{5}x=6−110−6=54,即 x=6.8x=6.8x=6.8。
- 当 [x]=7[x]=7[x]=7 时候,原方程为 x=(10−7)/(7−1)=3/6{x}=(10-7)/(7-1)=3/6x=(10−7)/(7−1)=3/6,即 x=7.5x=7.5x=7.5。
- 当 [x]=8[x]=8[x]=8 时候,原方程为 x=(10−8)/(8−1)=2/7{x}=(10-8)/(8-1)=2/7x=(10−8)/(8−1)=2/7,即 x=8+2/7x=8+2/7x=8+2/7。
- 当 [x]=9[x]=9[x]=9 时候,原方程为 x=(10−9)/(9−1)=1/8{x}=(10-9)/(9-1)=1/8x=(10−9)/(9−1)=1/8,即 x=9.125x=9.125x=9.125。
- 当 [x]=10[x]=10[x]=10 时候,原方程为 x=(10−10)/(10−1)=0{x}=(10-10)/(10-1)=0x=(10−10)/(10−1)=0,即 x=10x=10x=10。
关于 x 的方程 [x2]+[x3]=k[\frac{x}{2}]+[\frac{x}{3}]=k[2x]+[3x]=k 无解的自然数 k 排成一行,其前 2018 个 k 值之和等于多少?
思路
看到 x2\frac{x}{2}2x 和 x3\frac{x}{3}3x,自然想到了周期问题。
解题
222 和 333 的最小公倍数为 2×3=62 \times 3=62×3=6。因此对周期 666 进行枚举。
为了让大家更容易看出周期问题的套路,我们对 0∼110 \sim 110∼11 进行枚举。
| x | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| k=[x2]+[x3]k=[\frac{x}{2}]+[\frac{x}{3}]k=[2x]+[3x] | 0 | 0 | 1 | 2 | 3 | 3 |
| x | 6 | 7 | 8 | 9 | 10 | 11 |
| k=[x2]+[x3]k=[\frac{x}{2}]+[\frac{x}{3}]k=[2x]+[3x] | 5 | 5 | 6 | 7 | 8 | 8 |
如上图。
- x=0x=0x=0 与 x=6x=6x=6 是同周期的。
- x=1x=1x=1 与 x=7x=7x=7 是同周期的。
- .........
- x=5x=5x=5 与 x=11x=11x=11 是同周期的。
这样,我们可以轻易发现周期的规律。
- k=5×n+r,r∈[0,1,2,3]k=5\times n+r,\ r \in [0,1,2,3]k=5×n+r, r∈[0,1,2,3] 方程有解。
- k=5×n+r,r∈[4]k=5\times n+r,\ r \in [4]k=5×n+r, r∈[4] 方程无解。
这样,我们可以构造出所有解的序列为 k=5×n+4,n∈[0,1,2,...]k=5 \times n+4,\ n \in [0,1,2,...]k=5×n+4, n∈[0,1,2,...]。
这样前 201820182018 个 kkk 序列即为 4,9,14,...,5×2017+4=10,0894,9,14,...,5 \times 2017+4=10,0894,9,14,...,5×2017+4=10,089。
本题答案即为 ∑S=4+9+14+...+10089\sum S=4+9+14+...+10089∑S=4+9+14+...+10089。
根据等差数列求和公式可得,首项为 444,公差为 d=5d=5d=5,项数为 201820182018。
∑S=4×2018+2018×2017×52=10,183,837\sum S=4 \times 2018+\frac{2018 \times 2017 \times 5}{2}=10,183,837∑S=4×2018+22018×2017×5=10,183,837
相关文章:
)
数论 —— 高斯记号(Gauss mark)
定义 数学上,高斯记号(Gauss mark)是指对取整符号和取小符号的统称,用于数论等领域。 设 x∈Rx \in \textbf{R}x∈R,用 [x][x][x] 表示不超过 xxx 的最大整数。也可记作 [x][x][x]。设 x∈Rx \in \textbf{R}x∈R&…...

【随笔】程序员眼中的 CPU,“没有灵魂的躯体”
引言 先引用一段比较有意思的论述: 现实中每个人是由两部分构成,灵魂和躯体,灵魂依附于躯体游走于世间,现实中我们面对的每个人其实面对的是其灵魂而非肉体,肉体不过是表象而已。 灵魂本性乃一恶物,寄生于…...

算法的时间复杂度
算法在编写成可执行程序后,运行时需要消耗时间资源和空间(内存)资源,因此衡量一个算法的好坏,一般是从时间和空间两个维度来衡量的。 时间复杂度主要衡量一个算法运行的快慢,而空间复杂度主要衡量一个算法运…...
 | 机试题算法思路 【2023】)
华为OD机试 - 叠放书籍(Python) | 机试题算法思路 【2023】
最近更新的博客 华为OD机试 - 寻找路径 | 备考思路,刷题要点,答疑 【新解法】 华为OD机试 - 五键键盘 | 备考思路,刷题要点,答疑 【新解法】 华为OD机试 - IPv4 地址转换成整数 | 备考思路,刷题要点,答疑 【新解法】 华为OD机试 - 对称美学 | 备考思路,刷题要点,答疑 …...
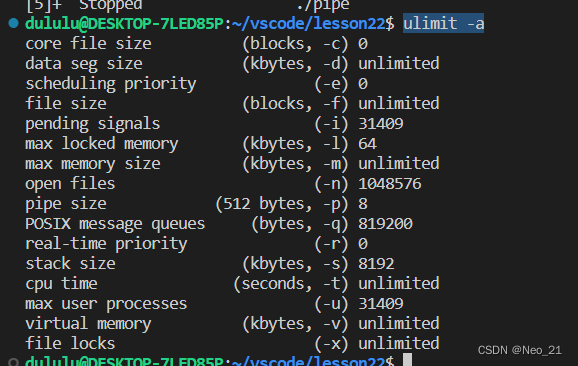
进程间通信(重点)
概念 进程是一个独立的资源分配单元,不同进程之间的资源是独立的进程并非孤立的,不同进程需要进行信息的交互和状态的传递,因此需要进程之间的通信【IPC: Inter processes communication】 如qq聊天,qq在每个人的手机上是独立的…...
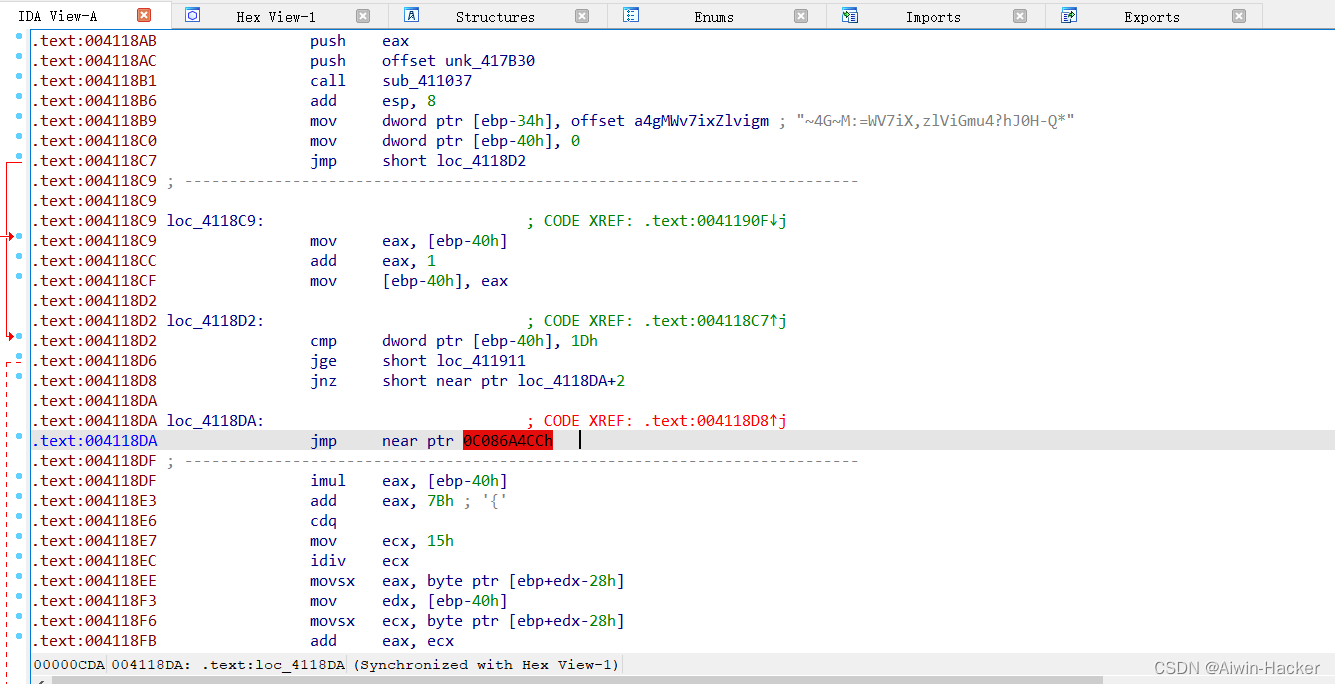
Reverse入门[不断记录]
文章目录前言一、[SWPUCTF 2021 新生赛]re1二、[SWPUCTF 2021 新生赛]re2三、[GFCTF 2021]wordy[花指令]四、[NSSRound#3 Team]jump_by_jump[花指令]五、[NSSRound#3 Team]jump_by_jump_revenge[花指令]前言 心血来潮,想接触点Reverse,感受下Reverse&am…...
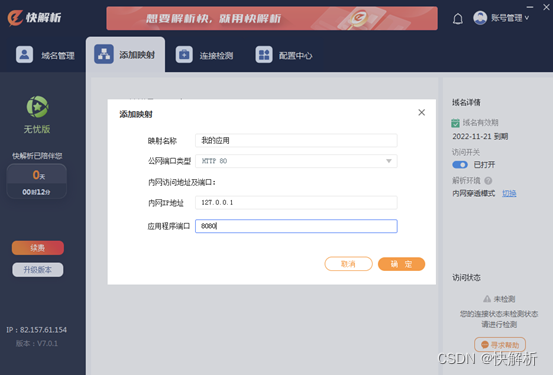
如何实现外网访问内网ip?公网端口映射或内网映射来解决
本地搭建服务器应用,在局域网内可以访问,但在外网不能访问。如何实现外网访问内网ip?主要有两种方案:路由器端口映射和快解析内网映射。根据自己本地网络环境,结合是否有公网IP,是否有路由权限,…...

[acwing周赛复盘] 第 91 场周赛20230218
[acwing周赛复盘] 第 91 场周赛20230218 一、本周周赛总结二、 4861. 构造数列1. 题目描述2. 思路分析3. 代码实现三、4862. 浇花1. 题目描述2. 思路分析3. 代码实现四、4863. 构造新矩阵1. 题目描述2. 思路分析3. 代码实现六、参考链接一、本周周赛总结 这周挺难的。T1 贪心分…...

蓝桥12届
小蓝准备用 256MB 的内存空间开一个数组,数组的每个元素都是 32 位 二进制整数,如果不考虑程序占用的空间和维护内存需要的辅助空间,请问 256MB 的空间可以存储多少个 32 位二进制整数?1MB 1024KB 1KB 1024字节(byte) 1字节 8位…...
)
华为OD机试 - 斗地主(JS)
斗地主 题目 斗地主起源于湖北十堰房县, 据传是一位叫吴修全的年轻人根据当地流行的扑克玩法“跑得快”改编的, 如今已风靡整个中国,并流行于互联网上 牌型: 单顺,又称顺子,最少5张牌,最多12张牌(3...A),不能有2, 也不能有大小王,不计花色 例如:3-4-5-7-8,7-8-9-1…...

【MyBatis】| MyBatis的注解式开发
目录 一:MyBatis的注解式开发 1. Insert注解 2. Delete注解 3. Update注解 4. Select注解 5. Results注解 一:MyBatis的注解式开发 MyBatis中也提供了注解式开发⽅式,采⽤注解可以减少Sql映射⽂件的配置。 当然,使⽤注…...
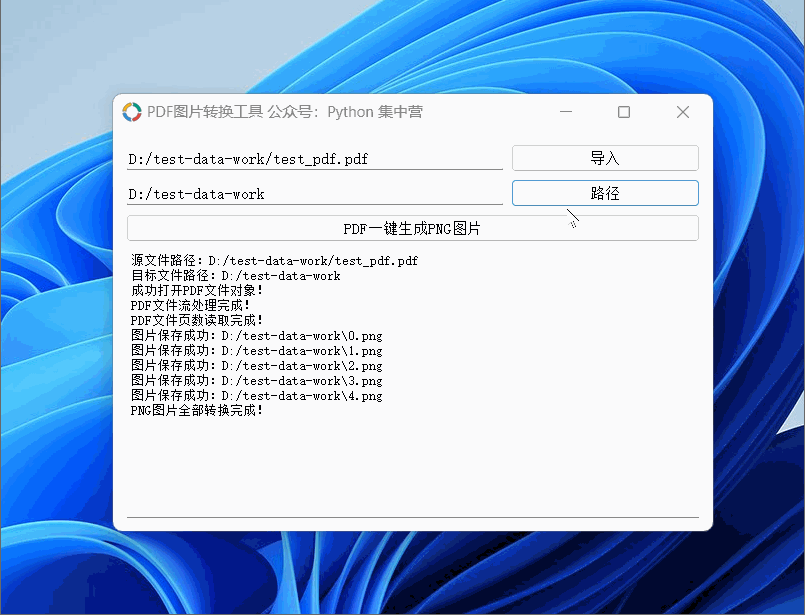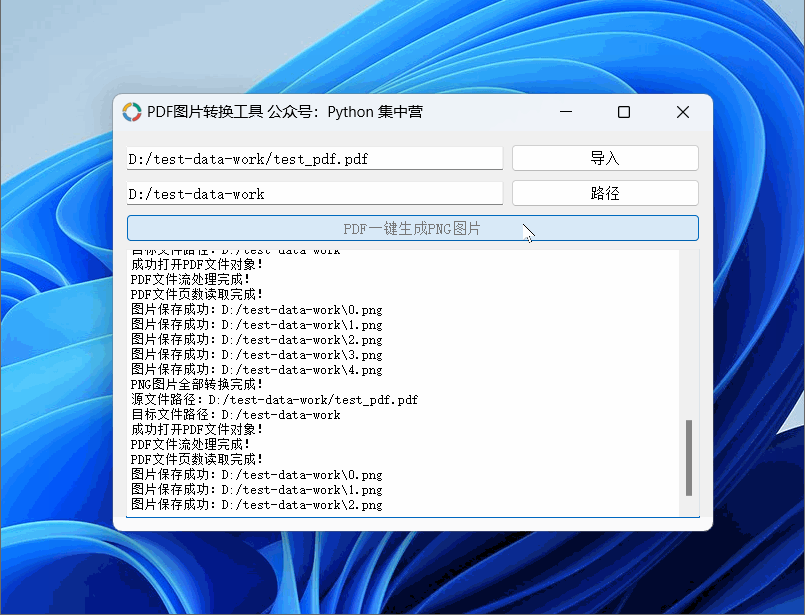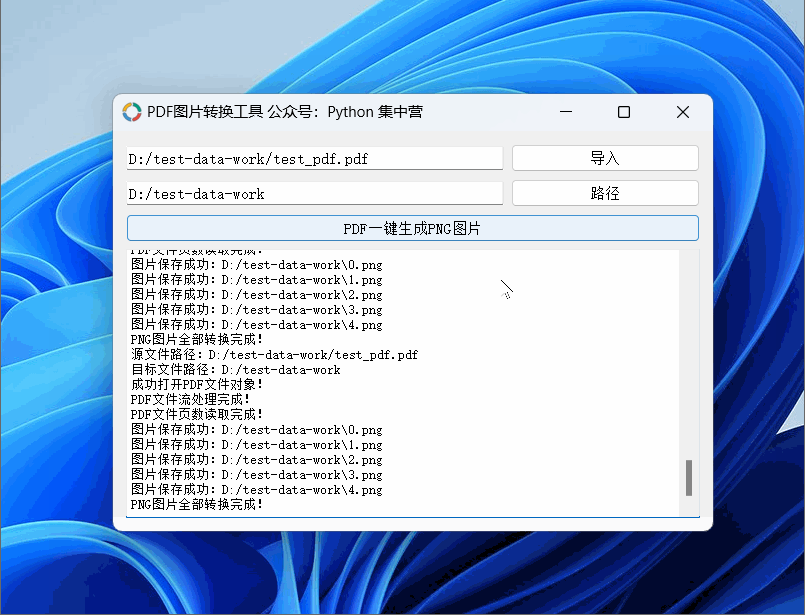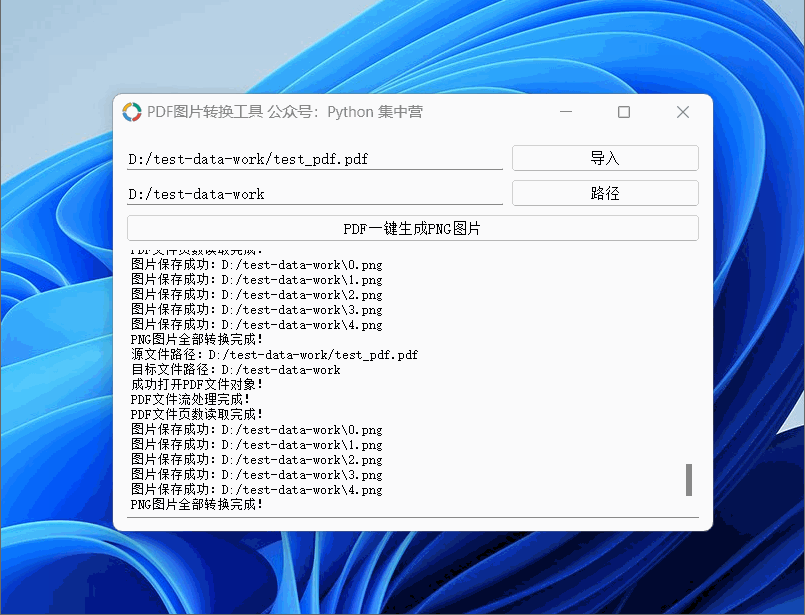
python自制PDF转换.PNG格式图片(按每页生成图片完整源码)小工具!
使用PyQt5应用程序制作PDF转换成图片的小工具,可以导入PDF文档后一键生成对应的PNG图片。 PDF图片转换小工具使用的中间件: python版本:3.6.8 UI应用版本:PyQt5 PDF文件操作非标准库:PyPDF2 PNG图片生成库࿱…...

Go 数组和切片反思
切片的底层数据结构是数组,所以,切片是基于数组的上层封装,使用数组的场景,也完全可以使用切片。 类型比较 我看到 go 1.17 有对切片和数组转换的优化,禁不住纳闷,有什么场景是必须数组来完成的呢&#x…...
win10电脑性能优化设置
win10电脑性能优化设置 目录win10电脑性能优化设置1.桌面图标显示2.wini2.1 “系统”2.1.1专注助手 关2.1.2 电源和睡眠 设置为从不2.1.3 存储 开2.2 网络和Internet2.3 个性化2.4 应用2.5 账户2.6 游戏2.7 隐私墨迹书写和键入个性化:关活动历史记录:全部…...

作为初学者必须要了解的几种常用数据库!
现在已经存在了很多优秀的商业数据库,如甲骨文(Oracle)公司的 Oracle 数据库、IBM 公司的 DB2 数据库、微软公司的 SQL Server 数据库和 Access 数据库。同时,还有很多优秀的开源数据库,如 MySQL 数据库,Po…...

小红书日常实习一面面经
时间:2月13下午 平台:赛码网,视频面大概70分钟顺序大致是下面,讲到哪问到哪,基础知识最好要结合项目或者实际回答,没录音不完全,有错误请指正首先面试官人超级好,细心提问,耐心解答问…...
)
将Nginx 核心知识点扒了个底朝天(一)
什么是Nginx? Nginx是一个 轻量级/高性能的反向代理Web服务器,用于 HTTP、HTTPS、SMTP、POP3 和 IMAP 协议。他实现非常高效的反向代理、负载平衡,他可以处理2-3万并发连接数,官方监测能支持5万并发,现在中国使用ngin…...

SSM项目搭建保姆级教程
文章目录1、什么是SSM框架1.1、持久层1.2、业务层1.3、表现层1.4、View层1.5、SpringMVC执行流程1.6、MyBatis2、SSM实战搭建2.1、创建工程2.2、添加依赖2.3、配置spring.xml文件2.4、配置web.xml文件2.5、log4j.properties2.6、准备表2.7、实体类2.8、mapper2.9、service2.10、…...

LeetCode 350. 两个数组的交集 II
原题链接 难度:easy\color{Green}{easy}easy 题目描述 给你两个整数数组 nums1nums1nums1 和 nums2nums2nums2 ,请你以数组形式返回两数组的交集。返回结果中每个元素出现的次数,应与元素在两个数组中都出现的次数一致(如果出现…...

Python可以解码吗,解码打码是如何实现的
前言 咳咳,进来的铁汁都是抱着学习的心态进来看的吧,咱今天不讲解解码,咱来说说python如何来实现打码功能~ 这一个个进来的 都是标题党吧哈哈哈 有兴趣的可以继续看看哦 最近重温了一档综艺节目 至于叫什么 这里就不细说了 老是看着看着就…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...

适应性Java用于现代 API:REST、GraphQL 和事件驱动
在快速发展的软件开发领域,REST、GraphQL 和事件驱动架构等新的 API 标准对于构建可扩展、高效的系统至关重要。Java 在现代 API 方面以其在企业应用中的稳定性而闻名,不断适应这些现代范式的需求。随着不断发展的生态系统,Java 在现代 API 方…...

elementUI点击浏览table所选行数据查看文档
项目场景: table按照要求特定的数据变成按钮可以点击 解决方案: <el-table-columnprop"mlname"label"名称"align"center"width"180"><template slot-scope"scope"><el-buttonv-if&qu…...

go 里面的指针
指针 在 Go 中,指针(pointer)是一个变量的内存地址,就像 C 语言那样: a : 10 p : &a // p 是一个指向 a 的指针 fmt.Println(*p) // 输出 10,通过指针解引用• &a 表示获取变量 a 的地址 p 表示…...
