第七讲---贪心(上课)

1.股票买卖
一、贪心

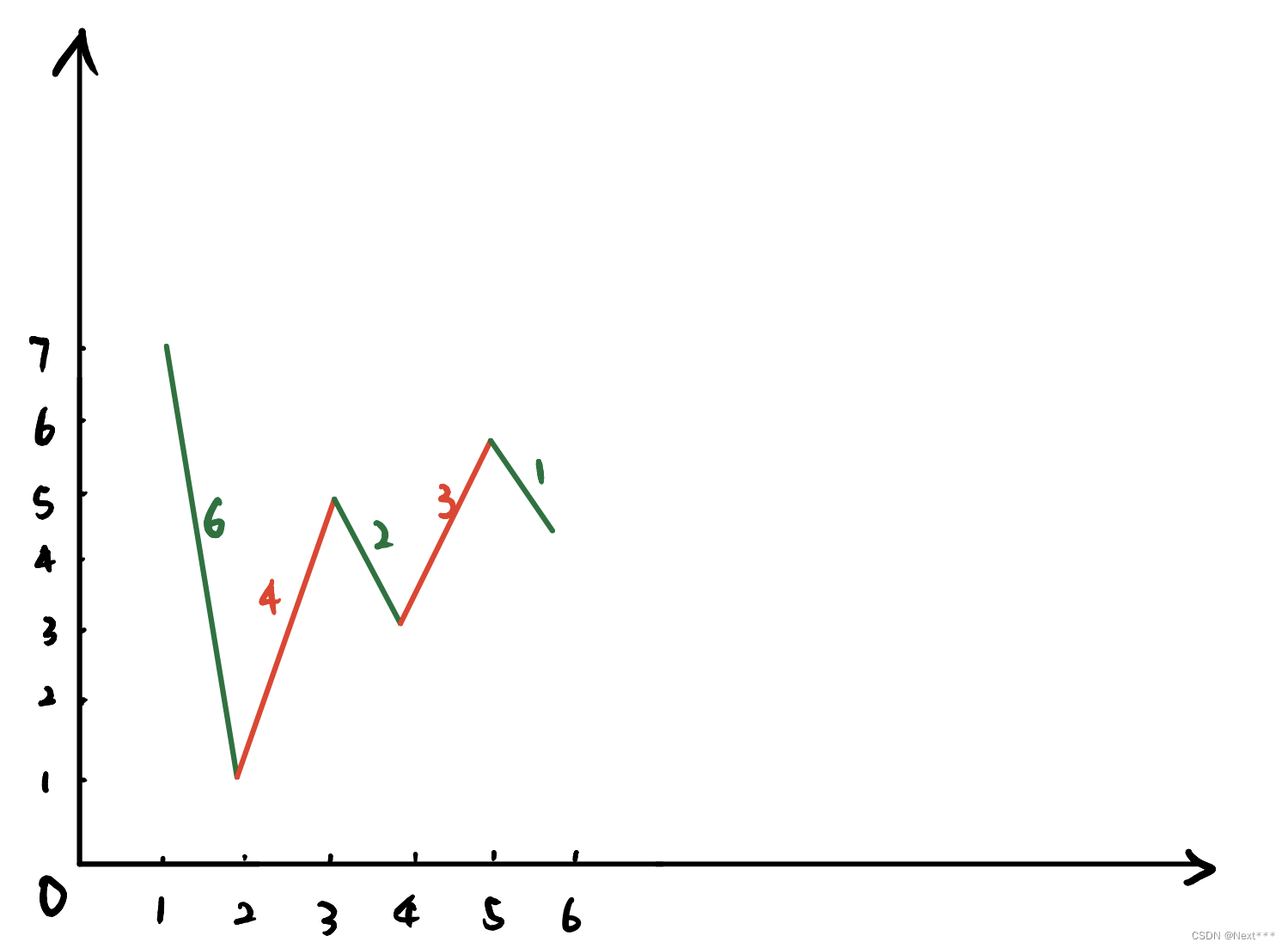
考虑一种方案,在每次上升的前一天购入股票,并在上升后的当天卖出的方案
if (w[i] > w[i - 1])res += w[i] - w[i - 1];
接下来证明该贪心思路得出的方案即是最优解。
(1)证明贪心解 ≥ 最优解:
由于贪心解都是取区间长度为 1 的解,因此假设存在于最优解中的某个区间 [i,j] 的长度 >1
那么会出现一下三种情况:
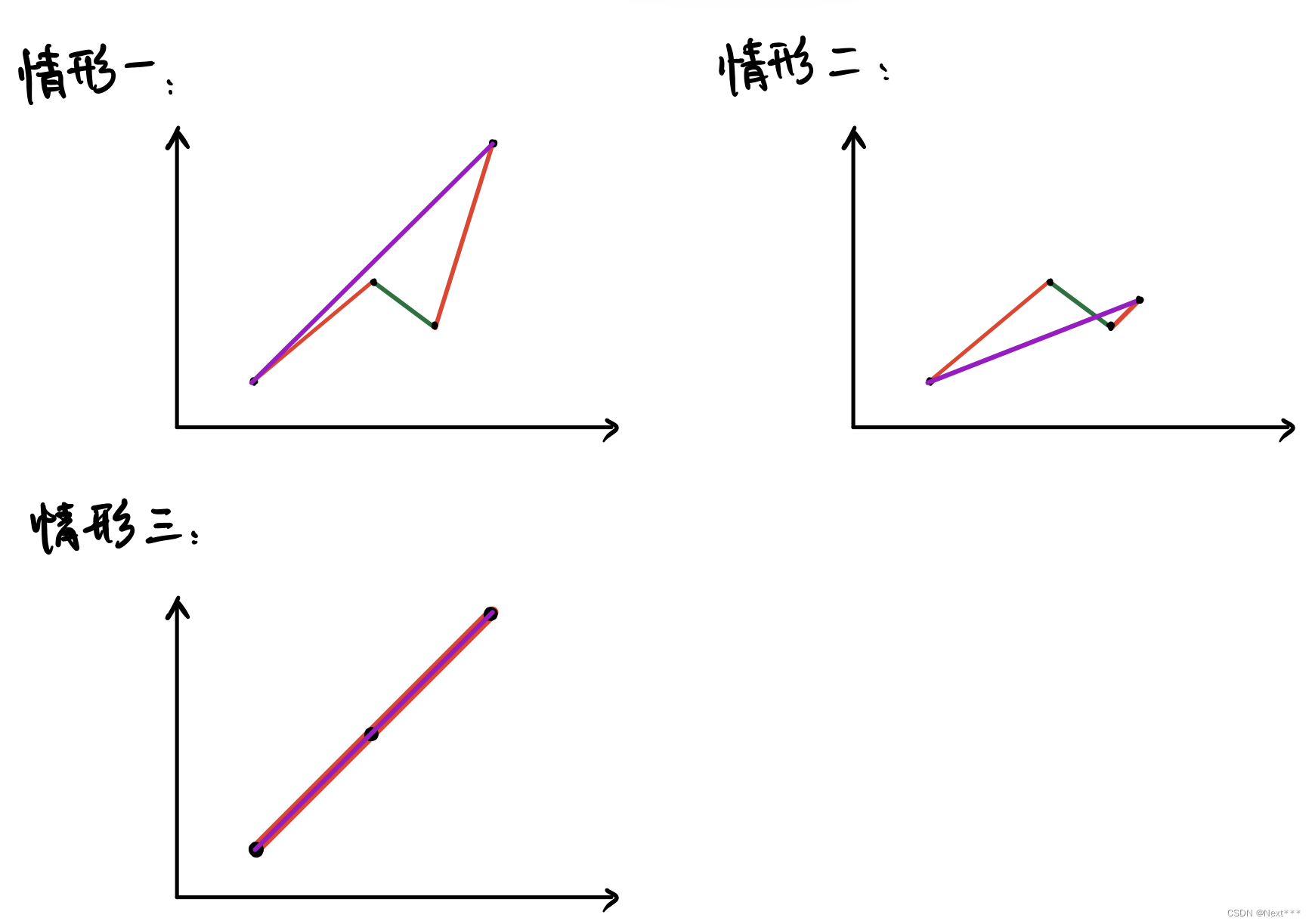
对应三种情形:最优解选取的区间最终点位于上方、下方、相等。
对于情形一:显然 最优解 < 贪心解
对于情形二:显然 最优解 <贪心解
对于情形三:毫无疑问,这就是存在于贪心解中的情形,因此 贪心解 = 最优解
得证
(2)证明贪心解 ≤最优解:
这部分无需证明,因为贪心解即是合法解,所以他的方案必定大于等于最优解
#include <iostream>
using namespace std;
const int N = 1e5 + 10;
int n;
int w[N];int main() {scanf("%d", &n);for (int i = 1; i <= n; ++i) scanf("%d", &w[i]);int res = 0;for (int i = 2; i <= n + 1; ++i) {if (w[i] - w[i - 1] > 0) res += w[i] - w[i - 1];}printf("%d\n", res);return 0;
}二、闫氏DP分析法
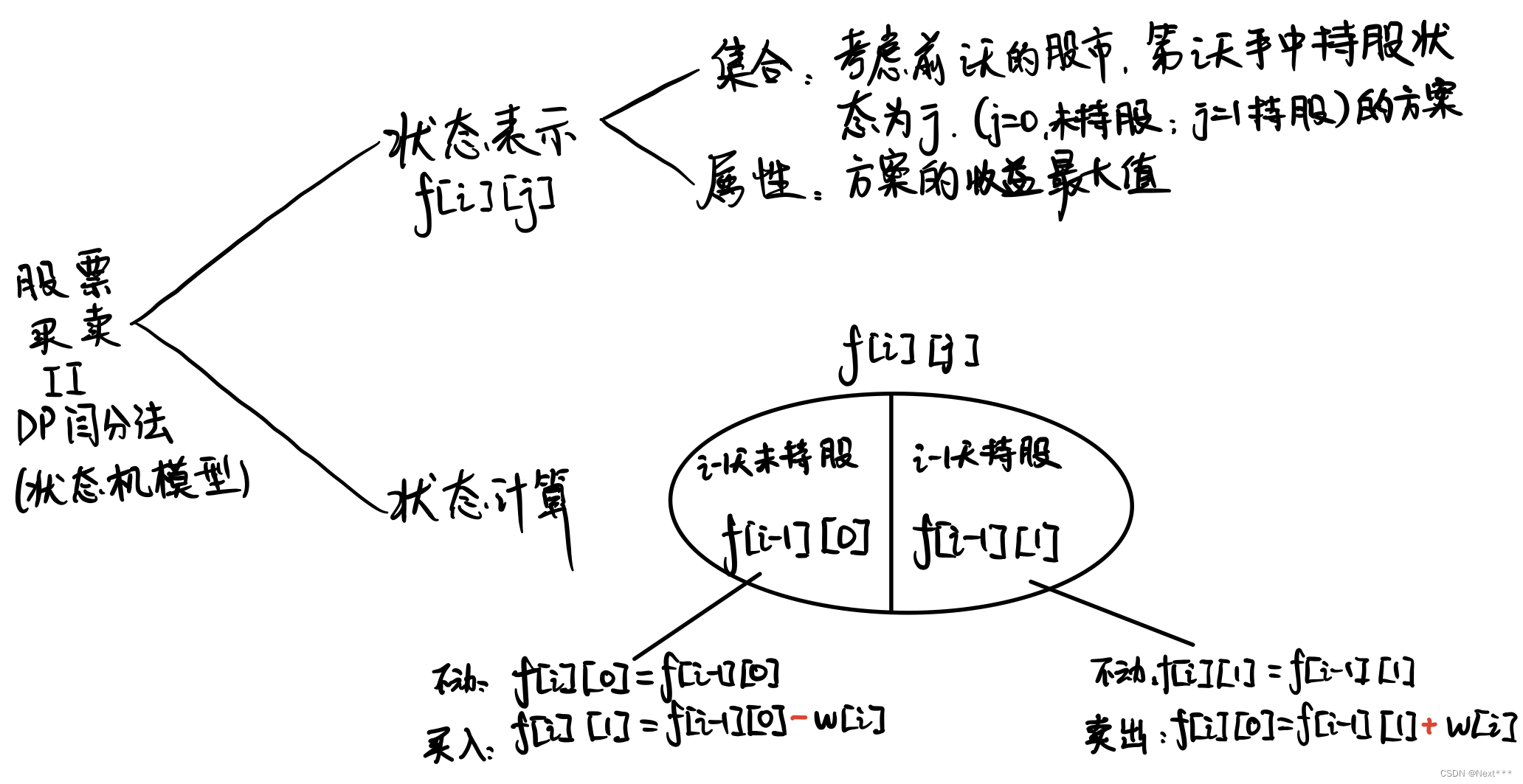
具体的状态机模型分析如下图:
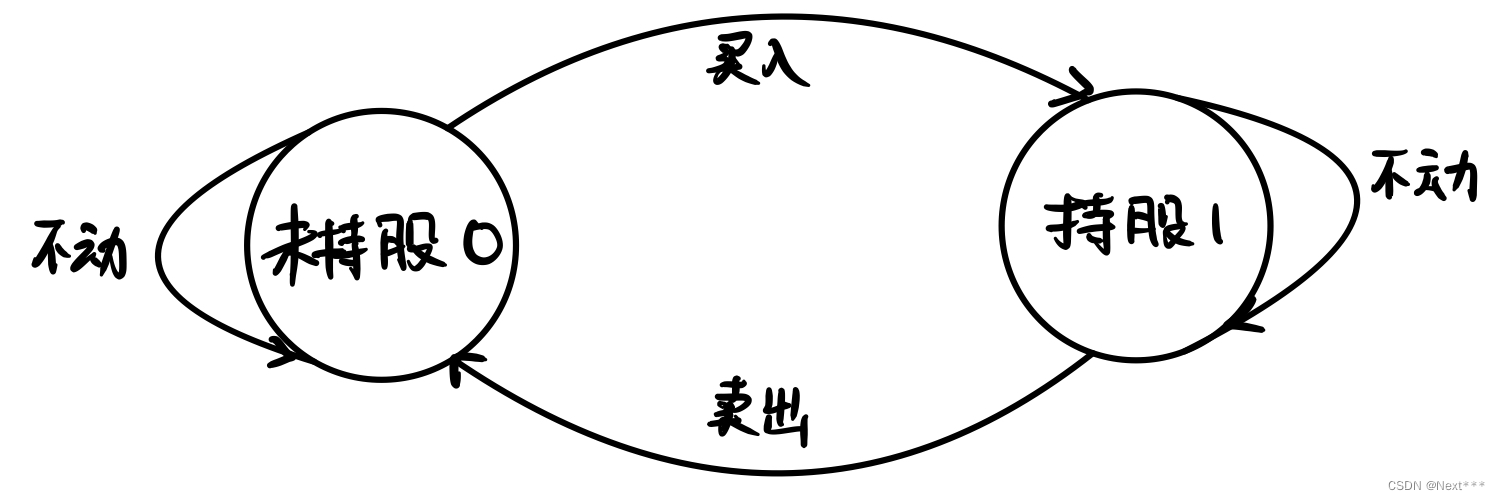
一共只2有种状态:
1. 当前处于未持股状态0:
对应可以进行的转换:
0->0 (不买入,继续观望,那么就什么都不发生)
0->1 (买入股票,那么收益就要减去当前市场的股票价格)
2. 当前处于持股状态1:
对应可以进行的转换:
1->1 (不卖出,继续观望,那么就什么都不发生)
1->0 (卖出股票,那么收益就要加上当前市场的股票价格)
#include <iostream>
using namespace std;
const int N = 1e5 + 10, INF = 0x3f3f3f3f;
int n;
int w[N];
int f[N][2];int main() {scanf("%d", &n);for (int i = 1; i <= n; ++i) scanf("%d", &w[i]);f[0][1] = -INF;for (int i = 1; i <= n; ++i) {f[i][0] = max(f[i - 1][0], f[i - 1][1] + w[i]);f[i][1] = max(f[i - 1][1], f[i - 1][0] - w[i]);}printf("%d\n", f[n][0]);return 0;
}2.货舱选址
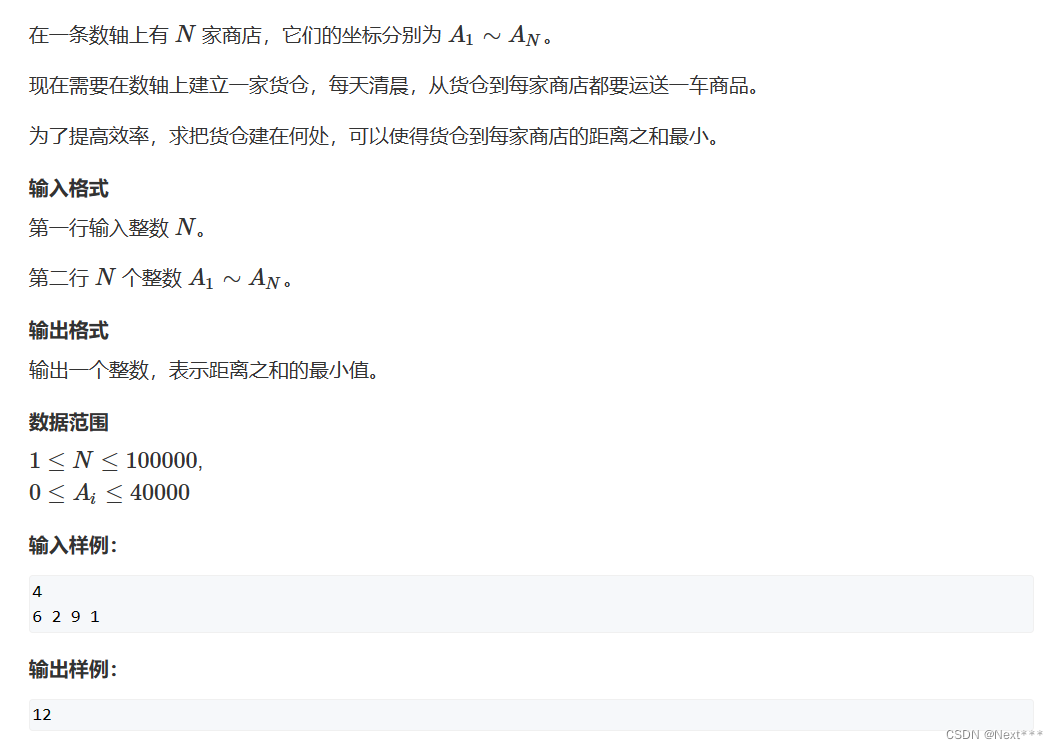
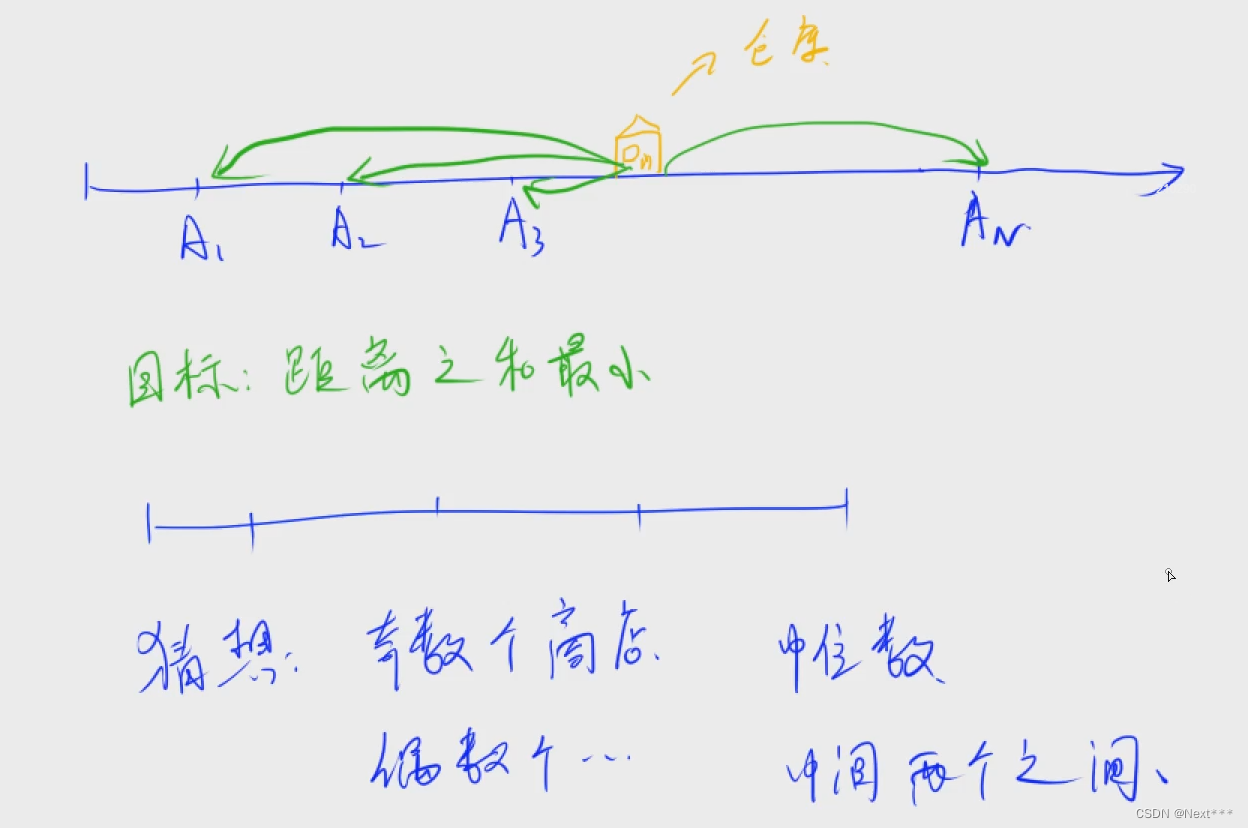

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 100010;
int n;
int a[N];
int main () {scanf ("%d",&n);for (int i = 1;i <= n;i++) scanf ("%d",&a[i]);sort (a + 1,a + 1 + n);int ans = 0;for (int i = 1,j = n;i <= j;i++,j--) ans += a[j] - a[i];printf ("%d\n",ans);return 0;
}
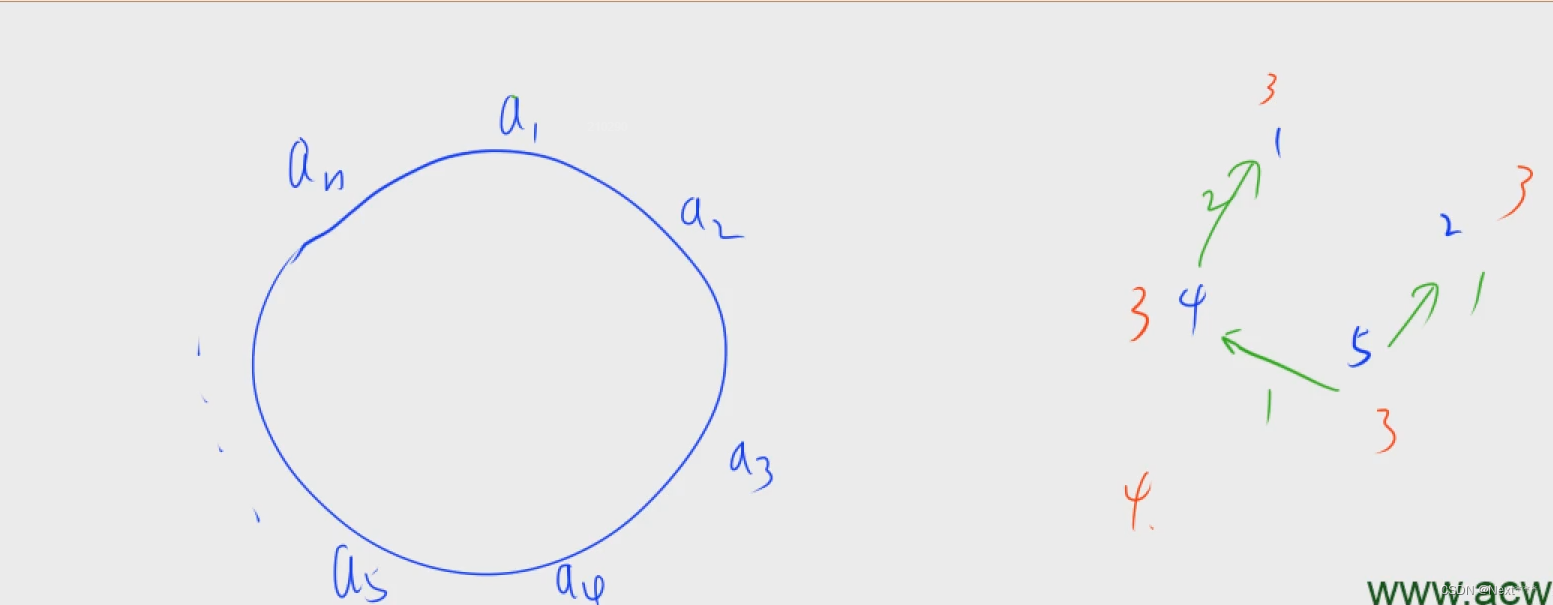
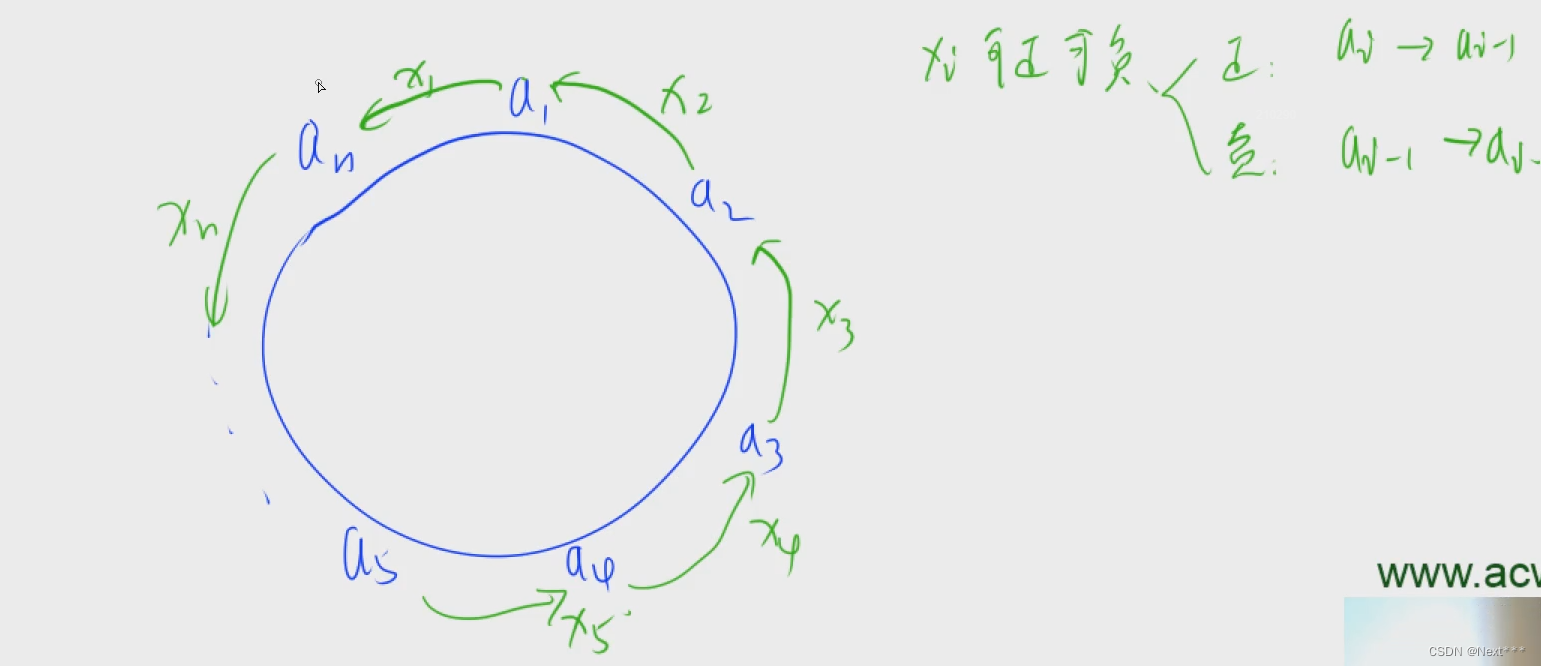
3.糖果传递
相关文章:

第七讲---贪心(上课)
1.股票买卖 一、贪心 考虑一种方案,在每次上升的前一天购入股票,并在上升后的当天卖出的方案 if (w[i] > w[i - 1])res w[i] - w[i - 1];接下来证明该贪心思路得出的方案即是最优解。 (1)证明贪心解 ≥ 最优解: …...

计算机如何思考与图灵完备
图灵完备是针对一套数据操作规则而言的概念,数据操作规则可以是一门编程语言,也可以是计算机实现里面的指令集,比如C/C++是图图灵完备的,通用CPU也是图灵完备的,但是GPU却不一定是图灵完备的。说白了图灵完备定义了一套规则,当这套规则可以实现图灵迹模型里的全部功能时,…...

惠普LaserJet M1005 MFP报错b2
故障现象: 惠普LaserJet M1005 MFP开机后直接报b2错误; 检测维修: 故障大意是:机器的硬件可能出现点突变,此问题建议联系当地维修中心进行处理。...
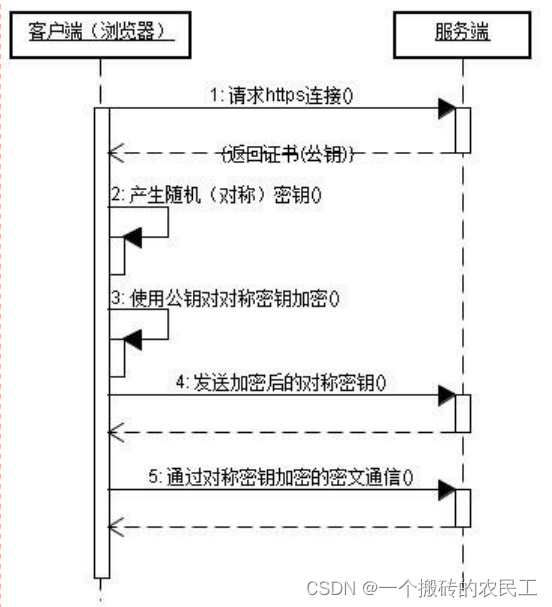
网络协议(TCP/IP)
目录一、网络分层模型二、OSI模型三、网络传输原理四、TCP/IP1、TCP/IP 原理2、TCP 三次握手/四次挥手3、Http协议和TCP/IP的区别五、HTTP原理六、HTTPS原理七、CDN原理一、网络分层模型 互联网的本质就是一系列的网络协议,最早由ISO国际组织定义为7层网络参考模型…...

2023河南省第二届职业技能大赛郑州市选拔赛“网络安全” 项目比赛样题任务书
2023河南省第二届职业技能大赛郑州市选拔赛“网络安全” 项目比赛样题任务书2023河南省第二届职业技能大赛郑州市选拔赛“网络安全” 项目比赛样题任务书A模块基础设施设置/安全加固(200分)A-1:登录安全加固(Windows, Linux&#…...

6、流程控制
目录一、if二、switch三、for四、break与continue五、goto与Label一、if if使用:逻辑表达式成立,就会执行{}里的内容;逻辑表达式不需要加() if 5 > 9 {fmt.Println("5>9") }if句子中允许包含1个(仅1个)分号:在分…...

Linux中最基本常见命令总结
❤❤💛💛💚💚💙💙💜💜您的认可是对我最大的帮助💜💜💙💙💚💚💛💛❤❤ 🤎&…...

Python学习-----模块2.0(常用模块之时间模块-->time)
目录 前言: time简介 导入模块 1.时间戳 2.时间元组 (1)把时间戳转换为元组形式 (2)元组转换为时间戳输出 (3)把元组转换为格式化时间 (4)把时间戳转换为格式化时间…...
XXL-JOB分布式任务调度框架(二)-策略详解
文章目录1.引言2.任务详解2.1.执行器2.2.基础配置3.路由策略(第一个)-案例4.路由策略(最后一个)-案例5.轮询策略-案例6.随机选取7.轮询选取8.一致性hash9.最不经常使用 (LFU)10.最近最久未使用(LRU)11.故障转移12.忙碌转移13.分片广播任务14.父子任务15.…...

JAVA练习54-最小栈
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 目录 前言 一、题目-最小栈 1.题目描述 2.思路与代码 2.1 思路 2.2 代码 总结 前言 提示:这里可以添加本文要记录的大概内容: 2月18日练习内容…...

Redis-哨兵模式以及集群
在开始这部分内容之前需要先说一下复制功能,因为这是Redis实现主从数据同步的实现方式。复制功能如果存在两台服务器的话,我们可以使用redis的复制功能,让一台服务器去同步另一台服务器的数据。现在我启动了两台redis服务器,一个端…...

过滤器和监听器
1、过滤器Filter 作用是防止SQL注入、参数过滤、防止页面攻击、空参数矫正、Token校验、Session验证、点击率统计等等; 使用Filter的步骤 新建类,实现Filter抽象类;重写init、doFilter、destroy方法;在SpringBoot入口中添加注解…...

Acwing 第 91 场周赛
Powered by:NEFU AB-IN B站直播录像! Link 文章目录Acwing 第 91 场周赛A AcWing 4861. 构造数列题意思路代码B AcWing 4862. 浇花题意思路代码C AcWing 4863. 构造新矩阵题意思路代码Acwing 第 91 场周赛 A AcWing 4861. 构造数列 题意 略 思路 将每个数的每一位…...
JavaEE|套接字编程之UDP数据报
文章目录一、DatagramSocket API构造方法常用方法二、DatagramPacket API构造方法常用方法E1:回显服务器的实现E2:带有业务逻辑的请求发送一、DatagramSocket API 在操作系统中,把socket对象当成了一个文件处理。等价于是文件描述符表上的一项。 普通的文件…...
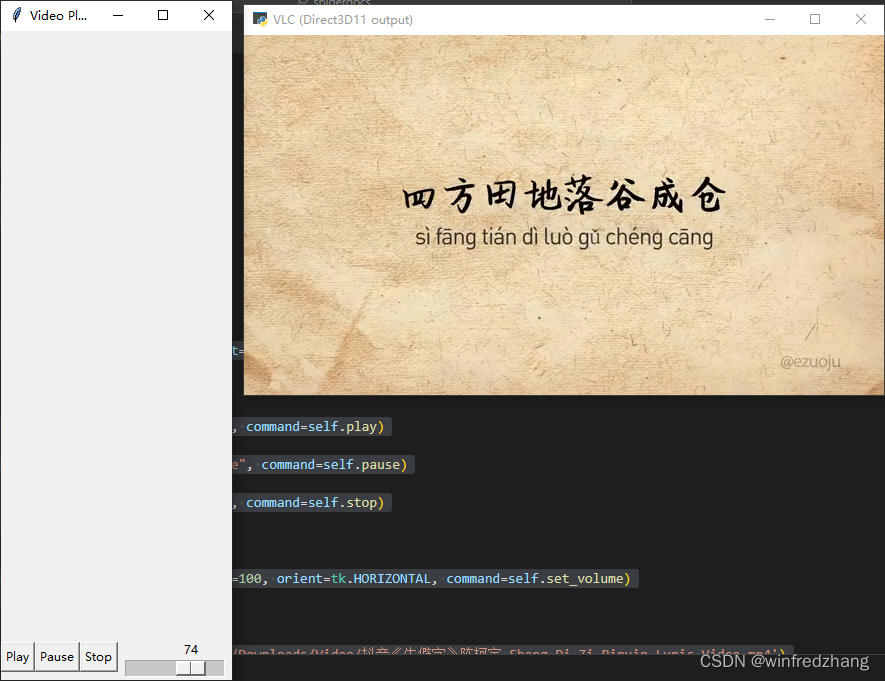
如何使用Python创建一个自定义视频播放器
目录 1、安装vlc的64位版本。 2、安装python的vlc模块。 3、编写如下代码,包含了播放,暂停,停止、音量控制功能。 4、来看一看运行结果。 5、如果遇到播放不了的问题,解决方式如下: 这个例子使用VLC作为视频播放器…...
和索引收缩(shrink ))
Elasticsearch进行优化-使用索引拆分(Split)和索引收缩(shrink )
一、索引拆分和收缩的场景 在Elasticsearch集群部署的初期我们可能评估不到位,导致分配的主分片数量太少,单分片的数据量太大,导致搜索时性能下降,这时我们可以使用Elasticsearch提供的Split功能对当前的分片进行拆分,…...
)
数论 —— 高斯记号(Gauss mark)
定义 数学上,高斯记号(Gauss mark)是指对取整符号和取小符号的统称,用于数论等领域。 设 x∈Rx \in \textbf{R}x∈R,用 [x][x][x] 表示不超过 xxx 的最大整数。也可记作 [x][x][x]。设 x∈Rx \in \textbf{R}x∈R&…...

【随笔】程序员眼中的 CPU,“没有灵魂的躯体”
引言 先引用一段比较有意思的论述: 现实中每个人是由两部分构成,灵魂和躯体,灵魂依附于躯体游走于世间,现实中我们面对的每个人其实面对的是其灵魂而非肉体,肉体不过是表象而已。 灵魂本性乃一恶物,寄生于…...

算法的时间复杂度
算法在编写成可执行程序后,运行时需要消耗时间资源和空间(内存)资源,因此衡量一个算法的好坏,一般是从时间和空间两个维度来衡量的。 时间复杂度主要衡量一个算法运行的快慢,而空间复杂度主要衡量一个算法运…...
 | 机试题算法思路 【2023】)
华为OD机试 - 叠放书籍(Python) | 机试题算法思路 【2023】
最近更新的博客 华为OD机试 - 寻找路径 | 备考思路,刷题要点,答疑 【新解法】 华为OD机试 - 五键键盘 | 备考思路,刷题要点,答疑 【新解法】 华为OD机试 - IPv4 地址转换成整数 | 备考思路,刷题要点,答疑 【新解法】 华为OD机试 - 对称美学 | 备考思路,刷题要点,答疑 …...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

AxureRP-Pro-Beta-Setup_114413.exe (6.0.0.2887)
Name:3ddown Serial:FiCGEezgdGoYILo8U/2MFyCWj0jZoJc/sziRRj2/ENvtEq7w1RH97k5MWctqVHA 注册用户名:Axure 序列号:8t3Yk/zu4cX601/seX6wBZgYRVj/lkC2PICCdO4sFKCCLx8mcCnccoylVb40lP...

负载均衡器》》LVS、Nginx、HAproxy 区别
虚拟主机 先4,后7...

免费批量Markdown转Word工具
免费批量Markdown转Word工具 一款简单易用的批量Markdown文档转换工具,支持将多个Markdown文件一键转换为Word文档。完全免费,无需安装,解压即用! 官方网站 访问官方展示页面了解更多信息:http://mutou888.com/pro…...
