【图神经网络】图拉普拉斯滤波器如何实现全通、低通、高通滤波
【图神经网络】图拉普拉斯滤波器如何实现全通、低通、高通滤波
文章目录
- 【图神经网络】图拉普拉斯滤波器如何实现全通、低通、高通滤波
- 1. 前言
- 2. 符号说明
- 3. 三种滤波
- 3.1 全通滤波
- 3.2 低通滤波
- 3.2.1 平滑信号分析
- 3.2.2 广义拉普拉斯平滑滤波器
- 3.3 高通滤波
- 4. 总结
1. 前言
GCN:图卷积神经网络。它不同于只用于网格结构数据的传统模型:LSTM,CNN等。是一种处理广义拓扑图结构的数据,深入挖掘其特征和规律的工具。(社交网络,通信网络,蛋白质分子等),这里也捎带补充一下广义拓扑图的概念:将实体抽象成与大小形状无关的点,点之间连接成线形成的图。GCN的发展史如下:
- 2005年,Marco Gori等人发表了论文,首次提出了GNN的概念,在此之前,处理图数据的方法是在数据的预处理阶段将图转换为用一组向量表示。这种处理方法会丢失很多的结构信息,得到的结果会严重依赖于对图的预处理,GNN的提出能够将学习过程直接架构在图数据之上。
- 2009年,进一步的阐述了图神经网络,提出了一种监督的方法来训练GNN,但是,早期的研究都是以迭代的方式,通过RNN传播邻居消息,直到达到稳定的固定状态来学习节点的表示。这种计算消耗极大。
- 2012年,CNN在CV上取得了很好的成绩,于是开始将卷积应用在GNN中。
- 2013年,Bruna等人提出了GCN,这时候的GCN是基于频域卷积的。后来又有很多人对它进行改进,拓展,但是频域卷积在计算时需要同时处理整个图,并且需要承担矩阵分解时很高的时间复杂度。
- 2016年,Kipf等人将频域卷积的定义简化,使图卷积操作能够在空域进行,极大提高了图卷积模型的计算效率,同时,由于卷积滤波的高效性,GCN模型在很多图数据相关任务上取得了很好的成绩。
- 之后的近几年里,想频域卷积提出的那时候一样,更多的基于空域GCN的变体被开发出来。这类方法都统称为GNN。各种GNN模型,大大加强了对各类图数据的适应性。
- 2018年,该领域不约而同地同时发表3篇综述论文。
- 2019年,各大顶级学术会议上GNN占据很大份额。
将来GNN的趋势会只增不减,只要我们好好利用它,相信能够很好的收获。
2. 符号说明
图数据可以表示为具有节点集 V 和边集 E 的图G =(V,E),其中点集V,n=|V|是节点数。这些节点是由该特征来描述的。矩阵X∈Rn×f^{n×f}n×f,其中 f 为节点特征的维数。G的图结构可以用邻接矩阵A∈Rn×n^{n×n}n×n来描述,其中,如果节点 i 和节点 j 之间有一条边,则为AijA_{ij}Aij = 1,否则为0。对角度矩阵记为 D=diag(d1,···,dn),其中di=∑jAijd_i =\sum_j A_{ij}di=∑jAij。我们使用A~=A+I\tilde A=A+IA~=A+I 来表示添加了自循环的邻接矩阵和D~=D+I\tilde D=D+ID~=D+I。传统的图拉普拉斯矩阵为:L=D~−A~L = \tilde D - \tilde AL=D~−A~。然后归一化的邻接矩阵是A~^=D~−1/2A~D~−1/2\hat{\tilde{A}} = \tilde D ^{−1/2}\tilde A \tilde D ^{−1/2}A~^=D~−1/2A~D~−1/2。相应地,L~=I−A~^\tilde L = I − \hat{\tilde{A}}L~=I−A~^是归一化对称正半定图拉普拉斯矩阵。
3. 三种滤波
III、A~^\hat {\tilde{A}}A~^、L~\tilde LL~,分别对应有全通、低通、高通滤波的算子(图卷积核/滤波器)**
3.1 全通滤波
- 公式为:Zall=IXZ_{all} = IXZall=IX
全通滤波也即所有的信号都可以通过,即不对图信号做处理。
3.2 低通滤波
- 公式为:Zlow=A~^XZ_{low} = \hat {\tilde{A}} XZlow=A~^X
低通滤波本质上就是为了使图上的特征变得光滑。下面进行解释:
图学习的基本假设是,图上相邻的节点应该是相似的,因此在图域上的节点特征应该是平滑的。本节首先解释了平滑的意思;然后给出了广义拉普拉斯平滑滤波器的定义,并证明了它是一个平滑算子;最后回答了如何设计一个最优的拉普拉斯平滑滤波器。
3.2.1 平滑信号分析
从图信号处理的角度来解释平滑开始。以 x∈Rnx\in R^nx∈Rn 作为图上的信号,节点 iii 的信号就是一个标量,也就是xix_ixi。滤波矩阵为HHH,为了测量图信号xxx的平滑度,可以计算出图的拉普拉斯算子 LLL (L=D−AL = D - AL=D−A)和 xxx 上的瑞利商:
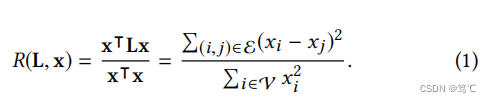
这个商实际上是xxx的标准化方差分数。如上所述,平滑信号应该在相邻节点上分配相似的值。因此,瑞利商越低,则图上的信号越平滑。
考虑图拉普拉斯L=UΛU−1L=UΛU^{−1}L=UΛU−1的特征分解,其中U∈Rn×nU \in R^{n\times n}U∈Rn×n包含特征向量,Λ=diag(λ1,λ2,⋅⋅⋅,λn)Λ = diag(λ1,λ2,···,λn)Λ=diag(λ1,λ2,⋅⋅⋅,λn)是特征值的对角矩阵。随后可以给出了特征向量 ui∈Uu_i \in Uui∈U的光滑性:
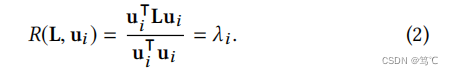
上式表示较平滑的特征向量与较小的特征值相关联,即频率较低。因此,基于等式基于LLL分解信号xxx基于公式(1)和(2):
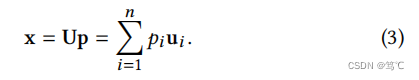
其中pip_ipi是特征向量uiu_iui的系数。那么xxx的平滑度就变成了:
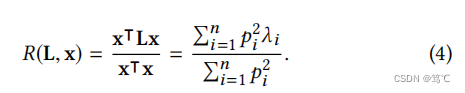
因此,为了获得更平滑的信号,滤波器的目标是:在保留低频分量的同时,滤掉高频分量。由于其高计算效率和令人信服的性能,拉普拉斯平滑滤波器经常被用于这一目的(保留低频分量的同时,滤掉高频分量)。
3.2.2 广义拉普拉斯平滑滤波器
广义拉普拉斯平滑滤波器定义为:

其中kkk是实值的。采用HHH作为滤波器矩阵,滤波后的信号 x~\tilde{x}x~ 被表示为:
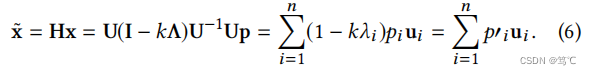
因此,为了实现低通滤波,频率响应函数1−kλ1−kλ1−kλ 应该是一个递减和非负函数。因为需要使特征值 λ 越大,对应的p′ip'ip′i系数就越小,这样可以使得图上的瑞丽商变小,进而光滑,进而实现低通(频率低的特征通过,频率低也就意味着光滑)。
注意,该过滤器是不含有参数的。
3.3 高通滤波
- 公式为:Zhigh=L~XZ_{high} = \tilde L XZhigh=L~X
说完低通滤波,高通滤波则与之相反。即不对这个函数进行限制。
此时,上述的公式(6)就变成了:
x~=Hx=UΛU−1Up=∑i=1nλipiui\tilde x = Hx = UΛU^{-1}Up = \sum^{n}_{i=1} λ_i p_i u_ix~=Hx=UΛU−1Up=∑i=1nλipiui
此时,uiu_iui 对应的图信号频率越高,其特征值 λ 越大,这样频率也就越大了,从而图上高频信号变多,进而实现了高通。
4. 总结
自己的理解罢了,可能不太到位,有什么想法,直接私信我就好!
相关文章:
【图神经网络】图拉普拉斯滤波器如何实现全通、低通、高通滤波
【图神经网络】图拉普拉斯滤波器如何实现全通、低通、高通滤波 文章目录【图神经网络】图拉普拉斯滤波器如何实现全通、低通、高通滤波1. 前言2. 符号说明3. 三种滤波3.1 全通滤波3.2 低通滤波3.2.1 平滑信号分析3.2.2 广义拉普拉斯平滑滤波器3.3 高通滤波4. 总结1. 前言 GCN&…...

python操作mysql数据库详解
使用Python操作MySQL数据库 MySQL是一种关系型数据库管理系统,它可以用来存储和管理大量的数据。之前介绍了大部分主流数据库,今天将介绍如何使用Python来操作MySQL数据库。 安装MySQL 首先,我们需要安装MySQL服务器,可以从MyS…...
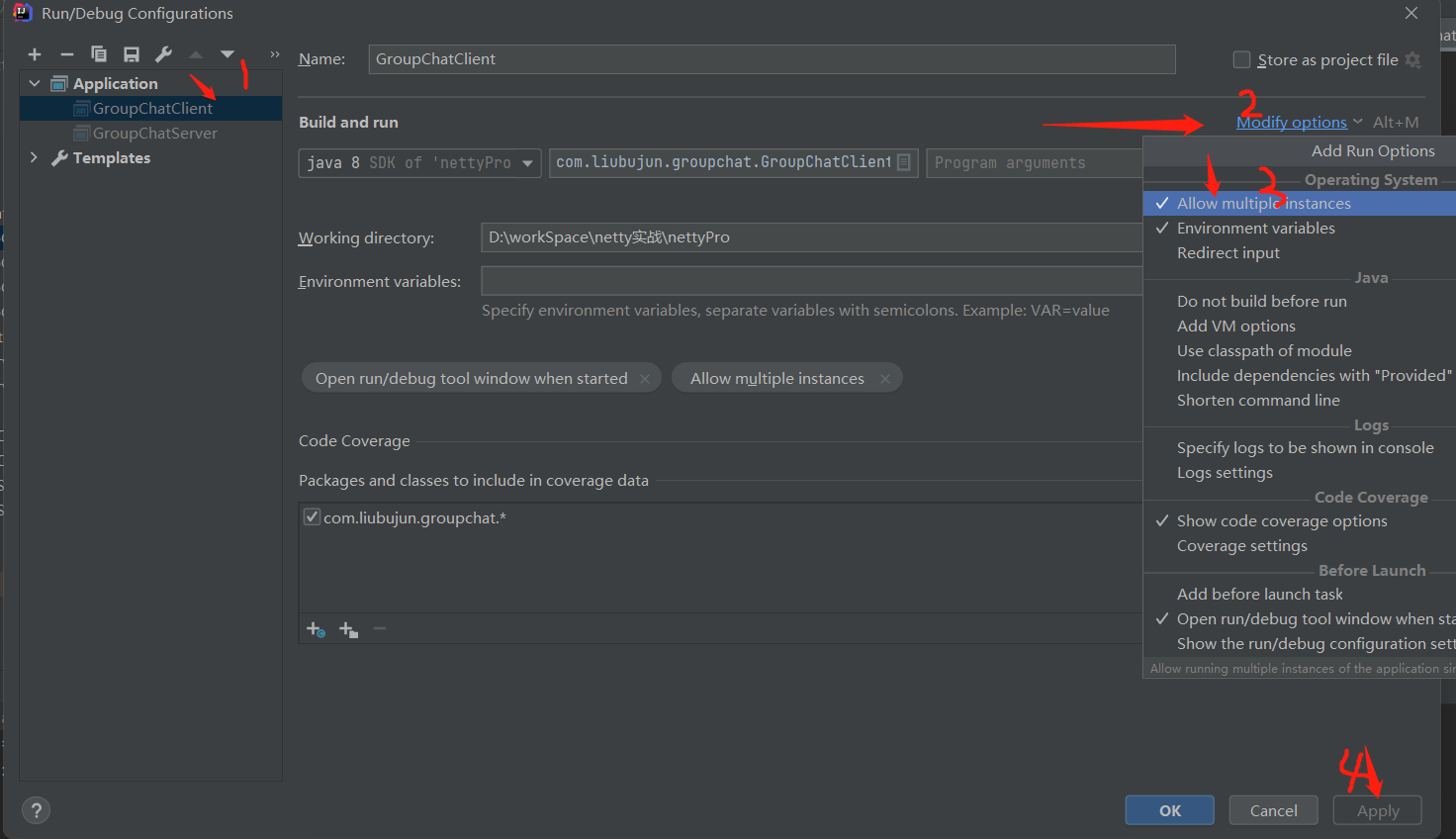
netty群聊系统
1设计思路:启动一个服务端,多个客户端第一个客户端启动时,会告诉服务器上线了第二个客户端启动时,告诉服务器上线,并且通知第一个启动的客户端第三个客户端启动时,告诉服务器上线,并且通知第一个…...
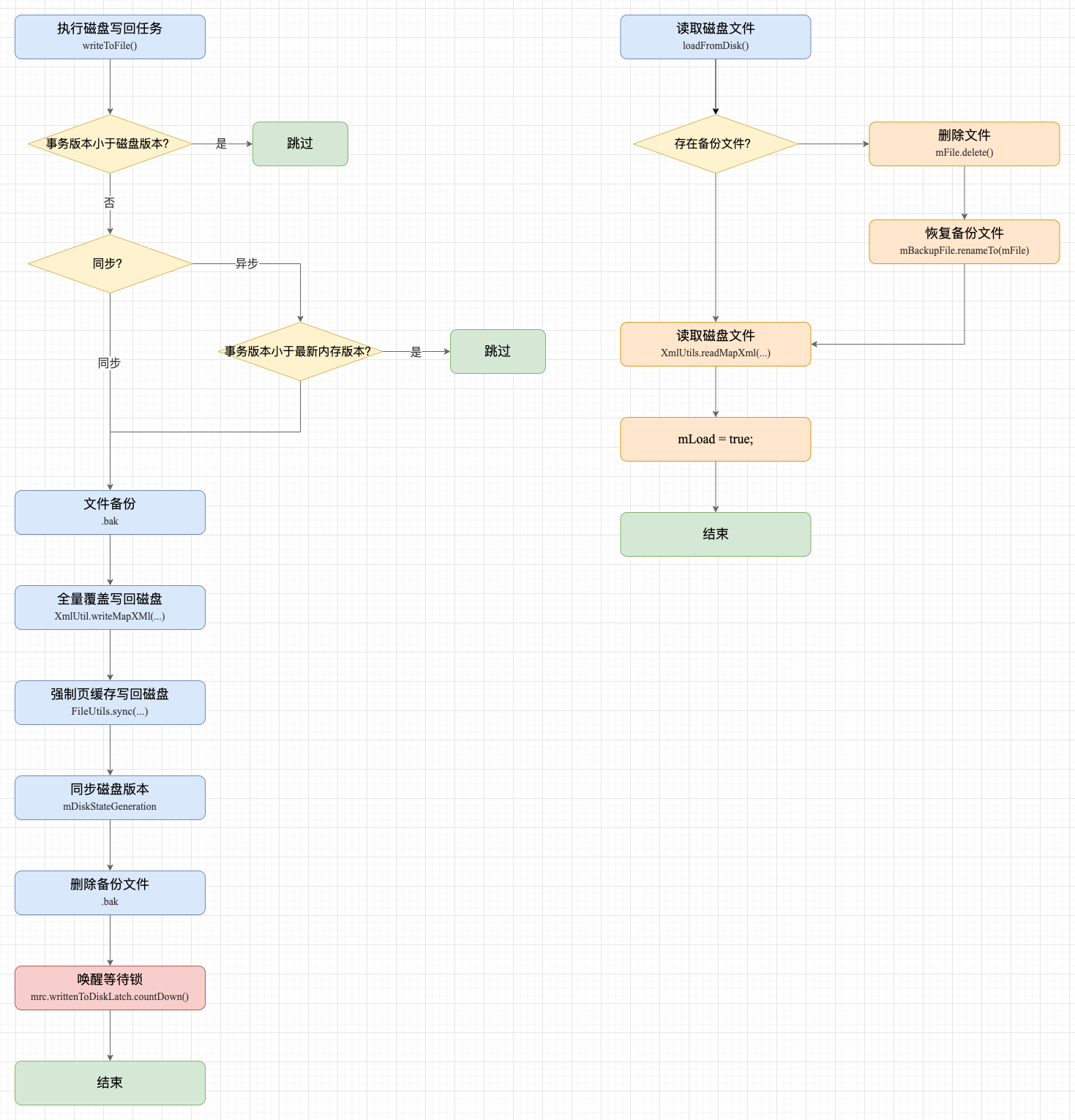
Android 初代 K-V 存储框架 SharedPreferences,旧时代的余晖?
本文已收录到 AndroidFamily,技术和职场问题,请关注公众号 [彭旭锐] 提问。 前言 大家好,我是小彭。 SharedPreferences 是 Android 平台上轻量级的 K-V 存储框架,亦是初代 K-V 存储框架,至今被很多应用沿用。 有的…...
在windows中使用tomcat搭建Jenkins
1、 准备环境:JDK JDK官网下载:https://download.oracle.com/java/19/latest/jdk-19_windows-x64_bin.msi 2、 tomcat包 tocat官网下载:https://tomcat.apache.org/download-90.cgi 3、 Jenkins.war包 Jenkins官网下载:https://mi…...

Linux系统
linux系统 世界上最重要的服务器端操作系统。 创建新目录 mkdir app mkdir -m 目录权限 目录名 创建有权限的目录名。 创建一个空白文件 touch app.txt创建一个文件。 cat创建一个文件。 vi/vim创建一个文件。 nano创建一个文件。 truncate创建一个文件。 pwd查看当前目录。 rm…...
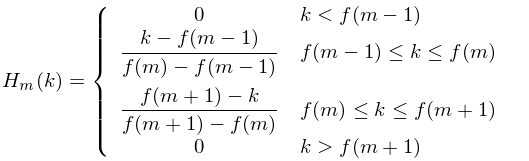
Mel Frequency Cepstral Coefficients (MFCCs)
wiki里说 在声音处理中,梅尔频率倒谱( MFC ) 是声音的短期功率谱的表示,基于非线性梅尔频率标度上的对数功率谱的线性余弦变换。 倒谱和MFC 之间的区别在于,在 MFC 中,频带在梅尔尺度上等距分布,这比正常频谱中使用的线…...
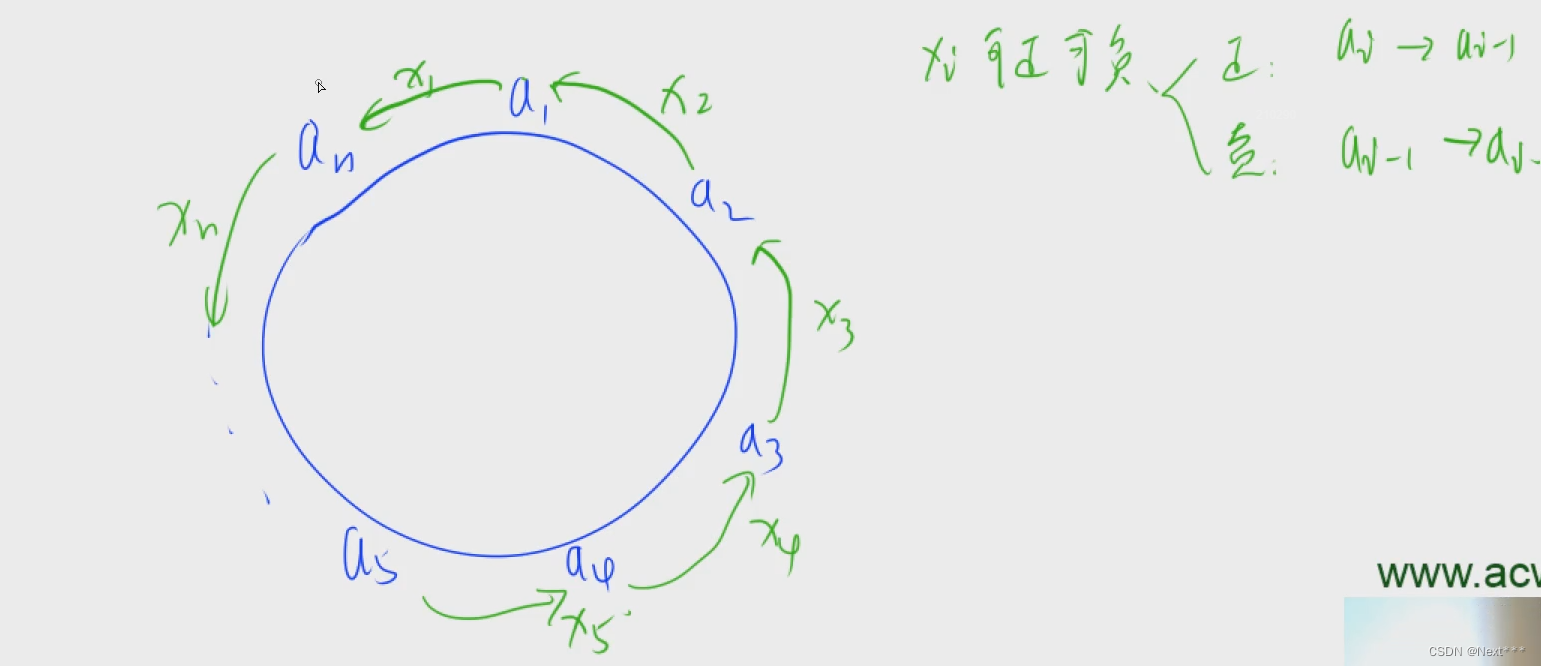
第七讲---贪心(上课)
1.股票买卖 一、贪心 考虑一种方案,在每次上升的前一天购入股票,并在上升后的当天卖出的方案 if (w[i] > w[i - 1])res w[i] - w[i - 1];接下来证明该贪心思路得出的方案即是最优解。 (1)证明贪心解 ≥ 最优解: …...

计算机如何思考与图灵完备
图灵完备是针对一套数据操作规则而言的概念,数据操作规则可以是一门编程语言,也可以是计算机实现里面的指令集,比如C/C++是图图灵完备的,通用CPU也是图灵完备的,但是GPU却不一定是图灵完备的。说白了图灵完备定义了一套规则,当这套规则可以实现图灵迹模型里的全部功能时,…...

惠普LaserJet M1005 MFP报错b2
故障现象: 惠普LaserJet M1005 MFP开机后直接报b2错误; 检测维修: 故障大意是:机器的硬件可能出现点突变,此问题建议联系当地维修中心进行处理。...
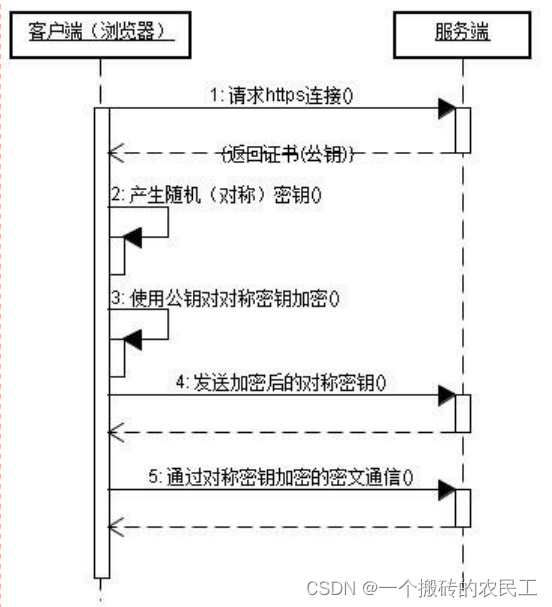
网络协议(TCP/IP)
目录一、网络分层模型二、OSI模型三、网络传输原理四、TCP/IP1、TCP/IP 原理2、TCP 三次握手/四次挥手3、Http协议和TCP/IP的区别五、HTTP原理六、HTTPS原理七、CDN原理一、网络分层模型 互联网的本质就是一系列的网络协议,最早由ISO国际组织定义为7层网络参考模型…...

2023河南省第二届职业技能大赛郑州市选拔赛“网络安全” 项目比赛样题任务书
2023河南省第二届职业技能大赛郑州市选拔赛“网络安全” 项目比赛样题任务书2023河南省第二届职业技能大赛郑州市选拔赛“网络安全” 项目比赛样题任务书A模块基础设施设置/安全加固(200分)A-1:登录安全加固(Windows, Linux&#…...

6、流程控制
目录一、if二、switch三、for四、break与continue五、goto与Label一、if if使用:逻辑表达式成立,就会执行{}里的内容;逻辑表达式不需要加() if 5 > 9 {fmt.Println("5>9") }if句子中允许包含1个(仅1个)分号:在分…...

Linux中最基本常见命令总结
❤❤💛💛💚💚💙💙💜💜您的认可是对我最大的帮助💜💜💙💙💚💚💛💛❤❤ 🤎&…...

Python学习-----模块2.0(常用模块之时间模块-->time)
目录 前言: time简介 导入模块 1.时间戳 2.时间元组 (1)把时间戳转换为元组形式 (2)元组转换为时间戳输出 (3)把元组转换为格式化时间 (4)把时间戳转换为格式化时间…...
XXL-JOB分布式任务调度框架(二)-策略详解
文章目录1.引言2.任务详解2.1.执行器2.2.基础配置3.路由策略(第一个)-案例4.路由策略(最后一个)-案例5.轮询策略-案例6.随机选取7.轮询选取8.一致性hash9.最不经常使用 (LFU)10.最近最久未使用(LRU)11.故障转移12.忙碌转移13.分片广播任务14.父子任务15.…...

JAVA练习54-最小栈
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 目录 前言 一、题目-最小栈 1.题目描述 2.思路与代码 2.1 思路 2.2 代码 总结 前言 提示:这里可以添加本文要记录的大概内容: 2月18日练习内容…...

Redis-哨兵模式以及集群
在开始这部分内容之前需要先说一下复制功能,因为这是Redis实现主从数据同步的实现方式。复制功能如果存在两台服务器的话,我们可以使用redis的复制功能,让一台服务器去同步另一台服务器的数据。现在我启动了两台redis服务器,一个端…...

过滤器和监听器
1、过滤器Filter 作用是防止SQL注入、参数过滤、防止页面攻击、空参数矫正、Token校验、Session验证、点击率统计等等; 使用Filter的步骤 新建类,实现Filter抽象类;重写init、doFilter、destroy方法;在SpringBoot入口中添加注解…...

Acwing 第 91 场周赛
Powered by:NEFU AB-IN B站直播录像! Link 文章目录Acwing 第 91 场周赛A AcWing 4861. 构造数列题意思路代码B AcWing 4862. 浇花题意思路代码C AcWing 4863. 构造新矩阵题意思路代码Acwing 第 91 场周赛 A AcWing 4861. 构造数列 题意 略 思路 将每个数的每一位…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...

STM32HAL库USART源代码解析及应用
STM32HAL库USART源代码解析 前言STM32CubeIDE配置串口USART和UART的选择使用模式参数设置GPIO配置DMA配置中断配置硬件流控制使能生成代码解析和使用方法串口初始化__UART_HandleTypeDef结构体浅析HAL库代码实际使用方法使用轮询方式发送使用轮询方式接收使用中断方式发送使用中…...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...
