算法练习--动态规划 相关
文章目录
- 走方格的方案
走方格的方案
请计算n*m的棋盘格子(n为横向的格子数,m为竖向的格子数)从棋盘左上角出发沿着边缘线从左上角走到右下角,总共有多少种走法,要求不能走回头路,即:只能往右和往下走,不能往左和往上走。
注:沿棋盘格之间的边缘线行走
输入描述:
输入两个正整数n和m,用空格隔开。(1≤n,m≤8)
输出描述:
输出一行结果
示例1
输入:
2 2
输出:
6
python实现:
- 递归
- 第一步向右 的方法数 + 第一步向下的方法数
- 类似爬楼梯
def func(n, m):if n < 0 or m < 0:return 0 # 没法走elif n == 0 or m == 0:return 1return func(n-1, m) + func(n, m-1)def walk():n, m = input().strip().split()n = int(n)m = int(m)return func(n, m)print(walk())
- 阶乘
import math
def walk():row, col = map(int, input().split())total_step = col + rowres = math.factorial(total_step) / (math.factorial(col) * math.factorial(row))print(int(res))walk()- 动态规划
- 构造二维数组
- 每个点的方法数= 上面点 + 左边点 方法数之和
def walk():n,m = map(int, input().split(' '))dp = [[1 for i in range(n+1)] for j in range(m+1)]for i in range(1,m+1):for j in range(1,n+1):dp[i][j] = dp[i-1][j]+dp[i][j-1]print(dp[m][n])walk()相关文章:

算法练习--动态规划 相关
文章目录 走方格的方案 走方格的方案 请计算n*m的棋盘格子(n为横向的格子数,m为竖向的格子数)从棋盘左上角出发沿着边缘线从左上角走到右下角,总共有多少种走法,要求不能走回头路,即:只能往右和…...

JAVA volatile 关键字
volatile 是JAVA虚拟机提供的轻量级的同步机制,有三大特性 1、保证可见性 2、不保证原子性 3、禁止指令重排 JMM JAVA内存模型本身是一种抽象的概念并不真实存在 它描述的是一组规则或规范,提供这组规范定义了程序中各个变量(包括实例变…...

[Leetcode] [Tutorial] 回溯
文章目录 46. 全排列Solution 78. 子集Solution 17. 电话号码的字母组合Solution 39. 组合总和Solution 22. 括号生成Solution 46. 全排列 给定一个不含重复数字的数组 nums ,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。 示例: 输入&…...
STM32 CubeMX USB_MSC(存储设备U盘)
STM32 CubeMX STM32 CubeMX USB_MSC(存储设备U盘) STM32 CubeMX前言 《使用内部Flash》——U盘一、STM32 CubeMX 设置USB时钟设置USB使能UBS功能选择FATFS功能 二、代码部分修改代码"usbd_storage_if.c"修改代码"user_diskio.c"main函数初始化插…...

湘大 XTU OJ 1214 A+B IV 题解:数位移动的本质+布尔变量标记+朴素模拟
一、链接 AB IV 二、题目 题目描述 小明喜欢做ab的算术,但是他经常忘记把末位对齐,再进行加,所以,经常会算错。 比如1213,他把12左移了1位,结果变成了133。 小明已经算了一些等式,请计算一下…...

以商业大数据技术助力数据合规流通体系建立,合合信息参编《数据经纪从业人员评价规范》团标
经国务院批准,由北京市人民政府、国家发展和改革委员会、工业和信息化部、商务部、国家互联网信息办公室、中国科学技术协会共同主办的2023 全球数字经济大会于近期隆重召开。由数交数据经纪(深圳)有限公司为主要发起单位,合合信息…...
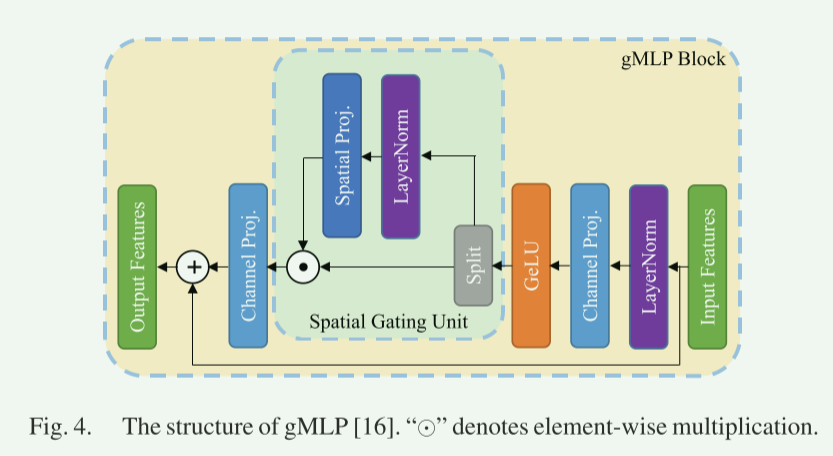
【论文阅读】Deep Instance Segmentation With Automotive Radar Detection Points
基于汽车雷达检测点的深度实例分割 一个区别: automotive radar 汽车雷达 : 分辨率低,点云稀疏,语义上模糊,不适合直接使用用于密集LiDAR点开发的方法 ; 返回的物体图像不如LIDAR精确,可以…...

易服客工作室:如何创建有用的内容日历
利用技巧和工具优化您的内容营销效率和效果。创建一个内容日历,您的整个团队都会从中受益! 欢迎来到熙熙攘攘、瞬息万变的内容营销世界,在这里,截止日期到来的速度比喝咖啡的猎豹还要快。 现在,想象一下在没有地图、…...

Excel革命,基于电子表格开发的新工具,不是Access和Power Fx
深谙其道 在日常工作中,Excel是许多人不可或缺的办公工具。 是微软的旗下产品,属于Microsoft 365套件中的一部分,强大的数据处理和计算功能,被普遍应用在全球各行各业的人群当中,是一款强大且普及的电子表格软件。 于…...

“崩溃”漏洞会影响英特尔 CPU 的使用寿命,可能会泄露加密密钥等
对于 CPU 安全漏洞来说,本周是重要的一周。昨天,不同的安全研究人员发布了两个不同漏洞的详细信息,一个影响多代英特尔处理器,另一个影响最新的 AMD CPU。“ Downfall ”和“ Inception ”(分别)是不同的错…...
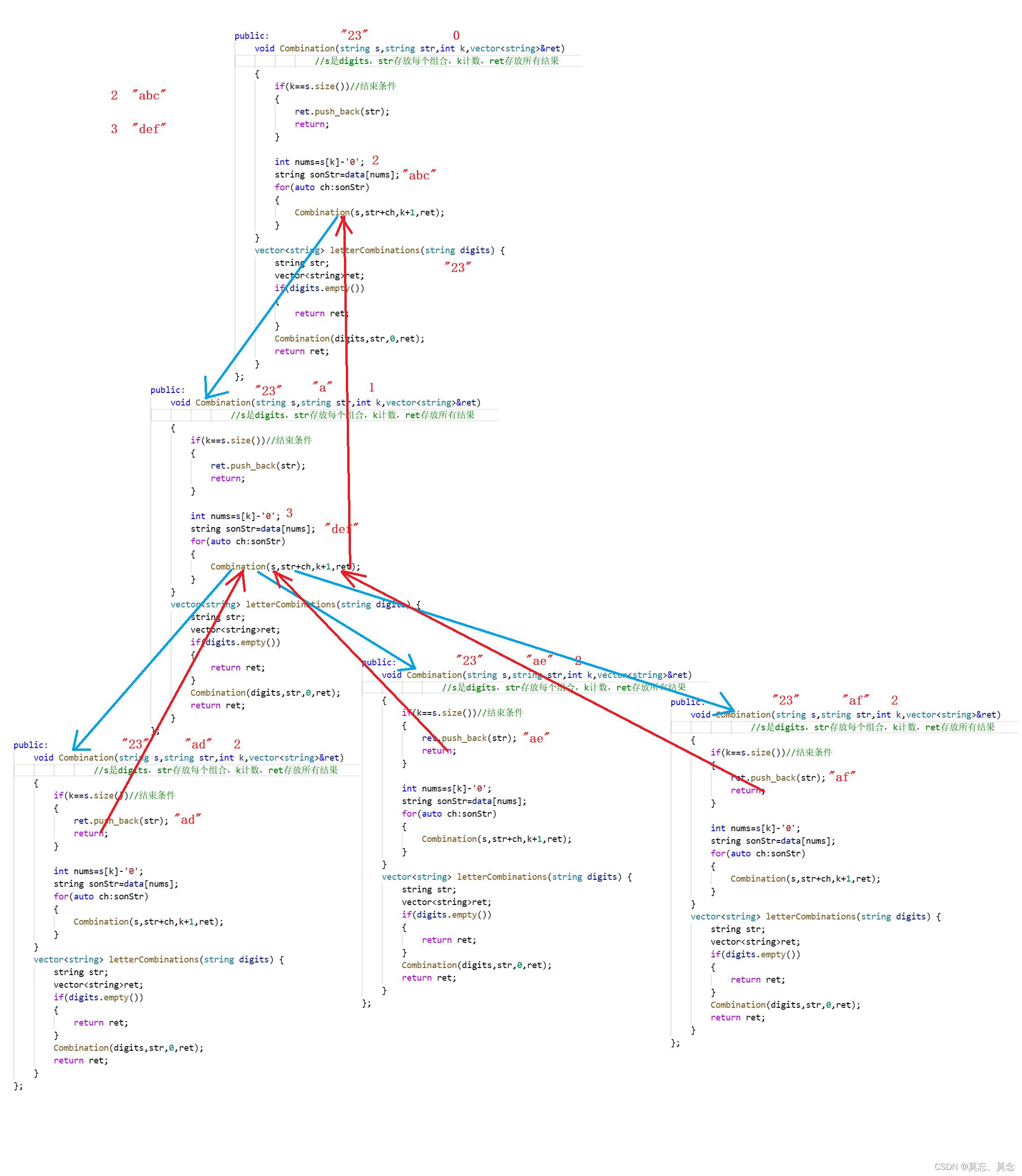
17.电话号码的字母组合(回溯)
目录 一、题目 二、代码 一、题目 17. 电话号码的字母组合 - 力扣(LeetCode) 二、代码 class Solution {const char*data[10]{"","","abc","def","ghi","jkl","mno","pq…...

Redis小例子
MAC电脑下Redis的安装: brew install redis下面给一个Java操作redis的小例子 import redis.clients.jedis.Jedis;public class Demo {public static void main(String[] args) {// 创建 Jedis 客户端实例,连接到本地 Redis 服务器,默认端口…...
ETLCloud+MaxCompute实现云数据仓库的高效实时同步
MaxCompute介绍 MaxCompute是适用于数据分析场景的企业级SaaS(Software as a Service)模式云数据仓库,以Serverless架构提供快速、全托管的在线数据仓库服务,消除了传统数据平台在资源扩展性和弹性方面的限制,最小化用…...

HTTP代理授权方式介绍
在网络爬虫过程中,我们经常需要使用HTTP代理来实现IP隐藏、突破限制或提高抓取效率。而为了确保代理的正常使用,并避免被滥用,代理服务商通常会采用授权方式。在本文中,我们将介绍几种常见的HTTP代理授权方式,以帮助你…...
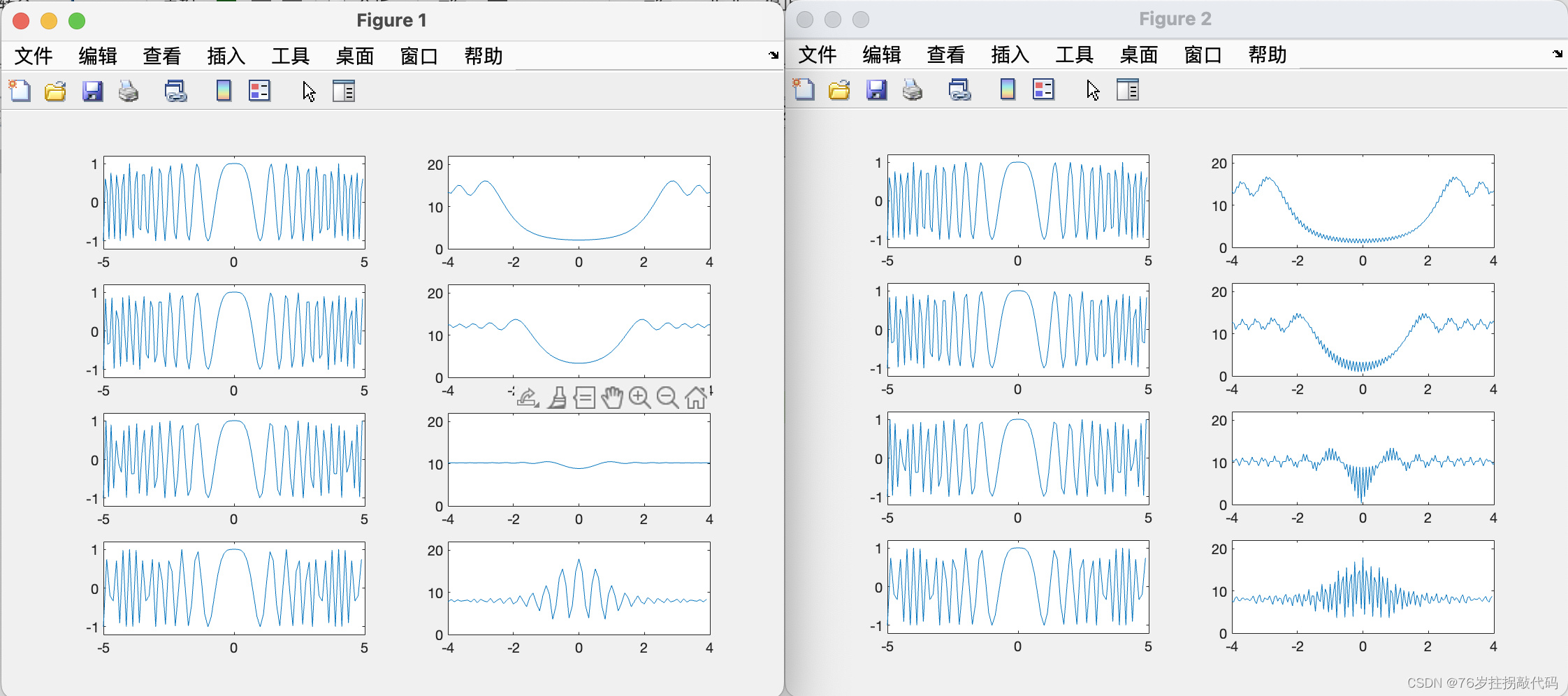
《合成孔径雷达成像算法与实现》Figure3.4
代码对补零信号与未补零信号都进行了实现,补零信号更加贴近书中图3.4的样子: clc clear all close all%参数设置 TBP 100; %时间带宽积 T 10e-6; %脉冲持续时间 alpha_os [1.4,1.2,1.0,0…...

qt5.15.2 使用mysql8.1
报错: QMYSQL driver not loaded 报错:无 QMYSQL 使用 QStringList drivers QSqlDatabase::drivers(); //获取现在可用的数据库驱动 foreach(QString driver, drivers) qDebug() << driver; “QSQLITE” “QMARIADB” “QMYSQL” “QMYSQL3” “…...

广州华锐互动:VR3D课程在线教育平台为职业院校提供沉浸式的虚拟现实学习体验
随着科技的飞速发展,虚拟现实(VR)和增强现实(AR)技术已经逐渐渗透到我们生活的各个领域。其中,VR3D课程在线教育平台作为一种新兴的教育方式,正在逐渐改变我们的学习方式和体验。本文将详细介绍VR3D课程在线教育平台的应用前景及特点。 VR3D课…...

clion run qt 问题汇总
一、Error copying file “D:/soft/QT/5.15.2/mingw81_64/bin/Qt5Cored.dll” to “D:/work/Ccode/qtproject/cmake-build-debug-qtmingw”.报错 查看路径下确实没有Qt5Cored.dll,只有Qt5Core.dll 注释掉cmakelist中的这三行 重新执行后成功 二、使用CLion编辑u…...

深入理解spring面经
1 了解SpringMVC的处理流程吗? 用户发送请求至前端控制器DispatcherServlet。DispatcherServlet通过处理器映射器HandlerMapping找到对应的处理器。DispatcherServlet将请求提交给对应的处理器Controller。Controller处理完请求后返回ModelAndView。DispatcherServ…...

2023年,App运行小游戏,可以玩出什么创意?
疫情过后,一地鸡毛。游戏行业的日子也不好过。来看看移动游戏收入:2022年,移动游戏收入达到920亿美元,同比下降6.4%。这告诉我们,2022年对移动游戏市场来说是一个小挫折。 但不管是下挫还是上升,移动游戏市…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...
 Module Federation:Webpack.config.js文件中每个属性的含义解释)
MFE(微前端) Module Federation:Webpack.config.js文件中每个属性的含义解释
以Module Federation 插件详为例,Webpack.config.js它可能的配置和含义如下: 前言 Module Federation 的Webpack.config.js核心配置包括: name filename(定义应用标识) remotes(引用远程模块࿰…...
