多源BFS
多源
- 超级源点和汇点
- 最短距离[超级汇点]
- 昂贵的聘礼
- 多源BFS
- 矩阵距离
超级源点和汇点
超级源点跟超级汇点是模拟出来的虚拟点,多用于图中:
<1>同时有多个汇点和一个源点,建立超级汇点
1、2、3、6分别到达4或者5或者7的最短路径,设立0这个超级汇点。
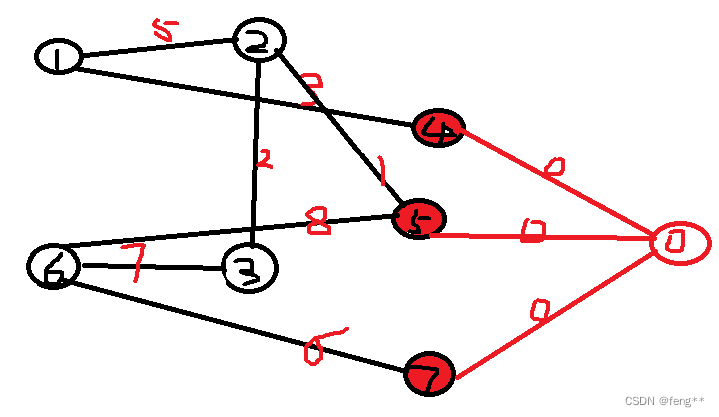
<2>同时有多个源点和一个汇点,建立超级源点
<3>同时有多个源点和多个汇点,建立超级源点和超级汇点
最短距离[超级汇点]
题目连接:https://www.acwing.com/problem/content/1490/
思路分析:这个题的关键就在于模拟出来一个超级汇点,对于每个村庄来说,目的地都是一个商店,具体是哪一个商店是不要求的,只需要找到最近的一个商店,也就是找到到这些商店集合的最短路径,虚拟出来一个超级汇点,到这些商店的路径都为0,这样每个村庄到达集合的最短路径其实就是到达这个超级汇点的最短路径了,也就相当于是这个超级汇点到每个点的最短路径,进行一次dijstra就行,也就简化成了求点到点的最短路径。
AC代码:
#include<iostream>
#include<queue>
#include<vector>
using namespace std;
const int N=100005;
const int INF=0x3f3f3f3f;
typedef pair<int,int>PII;
vector<PII>adj[N];
int dist[N];
bool visited[N];
int n,m,k,q,x;
priority_queue<PII,vector<PII>,greater<PII>>que;void dijistra(int s)
{for(int i=0;i<=n;i++) dist[i]=INF; dist[s]=0; que.push({0,s});while(!que.empty()){int min=que.top().second;que.pop();if(visited[min]) continue;visited[min]=true;for(int i=0;i<adj[min].size();i++){if(!visited[adj[min][i].first]&&dist[min]+adj[min][i].second<dist[adj[min][i].first]){dist[adj[min][i].first]=dist[min]+adj[min][i].second;que.push({dist[adj[min][i].first],adj[min][i].first});}}}
}
int main()
{cin>>n>>m;while(m--){int u,v,c; cin>>u>>v>>c; adj[u].push_back({v,c}); adj[v].push_back({u,c});}cin>>k;while(k--){cin>>x; adj[0].push_back({x,0}); adj[x].push_back({0,0});}dijistra(0); cin>>q; while(q--){cin>>x; cout<<dist[x]<<endl;}return 0;
}
昂贵的聘礼
刷题链接:https://www.acwing.com/problem/content/905/
思路分析:到底怎么建立图是很关键的,必要的时候要加一些超级源点和超级汇点
还是注意要建立一个超级源点,表示最后终止继续交换下去的那个人的花费是他的物品的价格;
最后要保证求出来的最短路包含的结点的等级相互之间都不超过m,只能是枚举这个等级区间了,不能说每次更新邻接结点的时候判断该结点距离当前纳入最短路径集合的结点的距离,如果超过了m就不更新,这样只能保证相邻的两个结点的等级是不超过m的,但是最后最短路径包含的全部结点相互间不一定都不超过m,规则是只要跟一个很高的人交换了,后面涉及的所有等级很低的人都不能再进行交换
AC代码:
#include<iostream>
#include<queue>
#include<vector>
#include<algorithm>
using namespace std;
const int N=105;
const int INF=0x3f3f3f3f;
typedef pair<int,int>PII; //first表示未结点编号,second表示到达该结点的优惠
vector<PII>adj[N];
int dist[N];
bool visited[N];
int m,n,p,l,x,t,v;
int Rank[N]; //存储每个结点的等级
priority_queue<PII,vector<PII>,greater<PII>>que;int dijistra(int down,int up) //传入区间等级最大和最小值
{for(int i=0;i<=n;i++){dist[i]=INF; visited[i]=false;}dist[0]=0;que.push({0,0});while(!que.empty()){int min=que.top().second;que.pop();if(visited[min]) continue;visited[min]=true;for(int i=0;i<adj[min].size();i++){//超级源点跟谁都能到达 if(Rank[adj[min][i].first]>up||Rank[adj[min][i].first]<down) continue; //等级相差太大,无法到达 if(!visited[adj[min][i].first]&&dist[min]+adj[min][i].second<dist[adj[min][i].first]){dist[adj[min][i].first]=dist[min]+adj[min][i].second;que.push({dist[adj[min][i].first],adj[min][i].first});}}}return dist[1];
}
int main()
{cin>>m>>n;for(int i=1;i<=n;i++){cin>>p>>l>>x;adj[0].push_back({i,p}); //建立超级源点到该点的边权Rank[i]=l;while(x--) //替代品们 {cin>>t>>v;adj[t].push_back({i,v}); //建立替代品到该点的边权} }int ans=INF;for(int i=Rank[1]-m;i<=Rank[1];i++){ans=min(ans,dijistra(i,i+m)); //超级源点到每个点的最短路径 }cout<<ans<<endl; return 0;
}
多源BFS
单源BFS:起始阶段只需要将某一个元素加入队列
二叉树层序遍历
多源BFS:开始阶段加入多个元素入队列,可以将其理解为存在一个超级源点,然后进行宽搜扩展,第一阶段会把距离为0的点扩展进队列进行求解最短距离,第二阶段会把距离为1的点扩展进队列进行求解最短距离,第三阶段会把距离为2的点扩展进队列进行求解最短距离,…最后成功将所有点距离目标点的最短距离求出来了。
矩阵距离
题目链接:https://www.acwing.com/problem/content/description/175/
思路分析:曼哈顿距离实际就是从1位置处向外扩展,每次扩展距离加1
AC代码:
#include<iostream>
#include<bits/stdc++.h>
using namespace std;
int n,m;
typedef pair<int,int>PII;
queue<PII>tou;
const int INF=0x3f3f3f3f;
const int N=1005;
int grid[N][N];
int off[4][2]={{0,-1},{0,1},{-1,0},{1,0}};
int main()
{cin>>n>>m;for(int i=0;i<n;i++){for(int j=0;j<m;j++){char t;cin>>t;if(t=='1') {grid[i][j]=0;tou.push({i,j});}else grid[i][j]=-1;}}while(!tou.empty()){int x=tou.front().first;int y=tou.front().second;tou.pop();for(int i=0;i<4;i++){int xi=x+off[i][0],yi=y+off[i][1];if(xi>=0 && yi>=0 &&xi<n && yi<m && grid[xi][yi]<0){tou.push({xi,yi});grid[xi][yi]=grid[x][y]+1;}}}for(int i=0;i<n;i++){for(int j=0;j<m;j++){cout<<grid[i][j]<<" ";}cout<<endl;}return 0;
}
相关文章:

多源BFS
多源 超级源点和汇点最短距离[超级汇点]昂贵的聘礼 多源BFS矩阵距离 超级源点和汇点 超级源点跟超级汇点是模拟出来的虚拟点,多用于图中: <1>同时有多个汇点和一个源点,建立超级汇点 1、2、3、6分别到达4或者5或者7的最短路径…...
自制电子农历
水文大师上线。今天一水电子农历牌。 首先讲讲电子配件,一来是电子小屏幕的选择,遇到文字比较多的,尤其是汉字,不要选传统那款128x64 oled,绝对放不下(找到最牛的超小免费字体至少要在8pixel以上才能看清楚)。我选了i…...
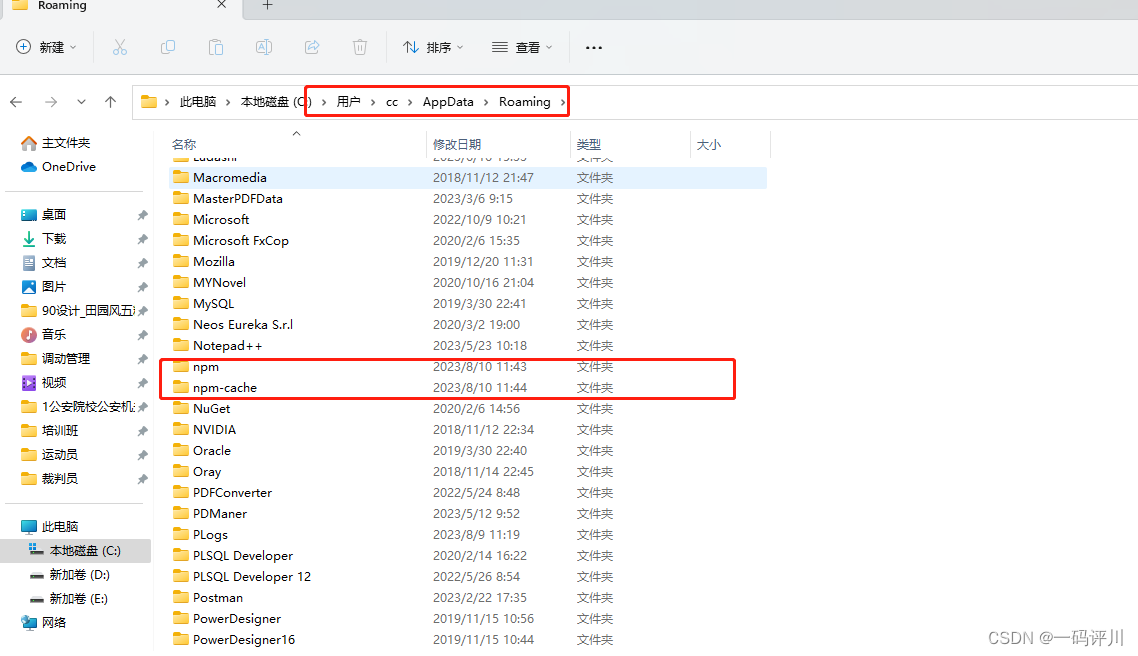
解决nvm安装后,node生效但npm无效
问题描述 nvm安装后,node生效但npm无效 清除缓存 C:\Users\cc\AppData\Roaming cc是我的用户名改成你自己的就行删除 npm和npm-cache...
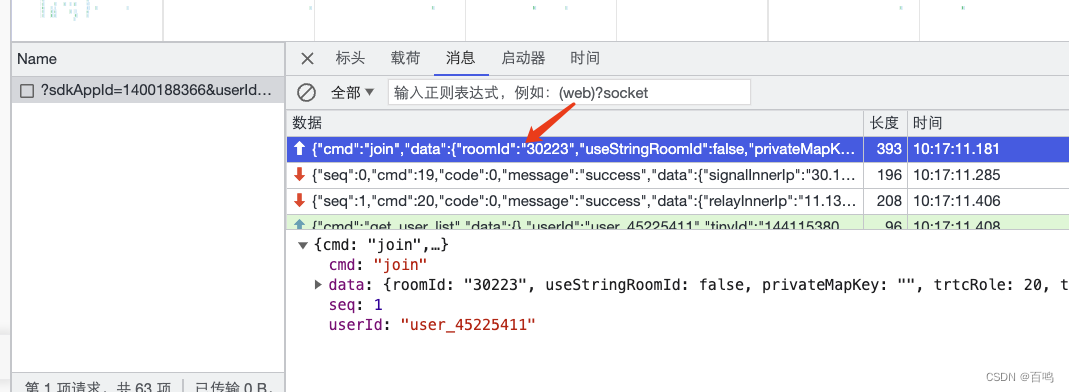
Chrome DevTools 与 WebSocket 数据查看失焦的问题
Chrome DevTools 在与 WebSocket 连接交互时可能会出现失焦的问题,这似乎是一个已知的 bug。当 DevTools 选中 WebSocket 消息时,如果有新的消息到达,DevTools 将会自动失焦,导致无法查看完整的消息内容。 虽然这个问题很令人困扰…...

Javascript 正则
基本语法 定义 JavaScript种正则表达式有两种定义方式 构造函数 var regnew RegExp(<%[^%>]%>,g);字面量 var reg/<%[^%>]%>/g;g: global,全文搜索,默认搜索到第一个结果接停止i:ingore case,忽略…...

C语言可变数组 嵌套的可变数组,翻过了山跨过了河 又掉进了坑
可变数组 专栏内容: postgresql内核源码分析 手写数据库toadb 并发编程 个人主页:我的主页 座右铭:天行健,君子以自强不息;地势坤,君子以厚德载物. 概述 数组中元素是顺序存放,这一特性让我们…...
FFmpeg安装和使用
sudo apt install ffmpeg sudo apt-get install libavfilter-devcmakelist模板 CMakeLists.txt cmake_minimum_required(VERSION 3.16) project(ffmpeg_demo)# 设置ffmpeg依赖库及头文件所在目录,并存进指定变量 set(ffmpeg_libs_DIR /usr/lib/x86_64-linux-gnu) …...

HTTP代理编程:Python实用技巧与代码实例
今天我要与大家分享一些关于HTTP代理编程的实用技巧和Python代码实例。作为一名HTTP代理产品供应商,希望通过这篇文章,帮助你们掌握一些高效且实用的编程技巧,提高开发和使用HTTP代理产品的能力。 一、使用Python的requests库发送HTTP请求&a…...
)
java调用第三方接口工具类 (HttpClientUtils.java)
1. 依赖 <!--httpclient--> <dependency><groupId>commons-httpclient</groupId><artifactId>commons-httpclient</artifactId><version>3.1</version> </dependency><!-- 阿里JSON解析器 --> <dependency>…...
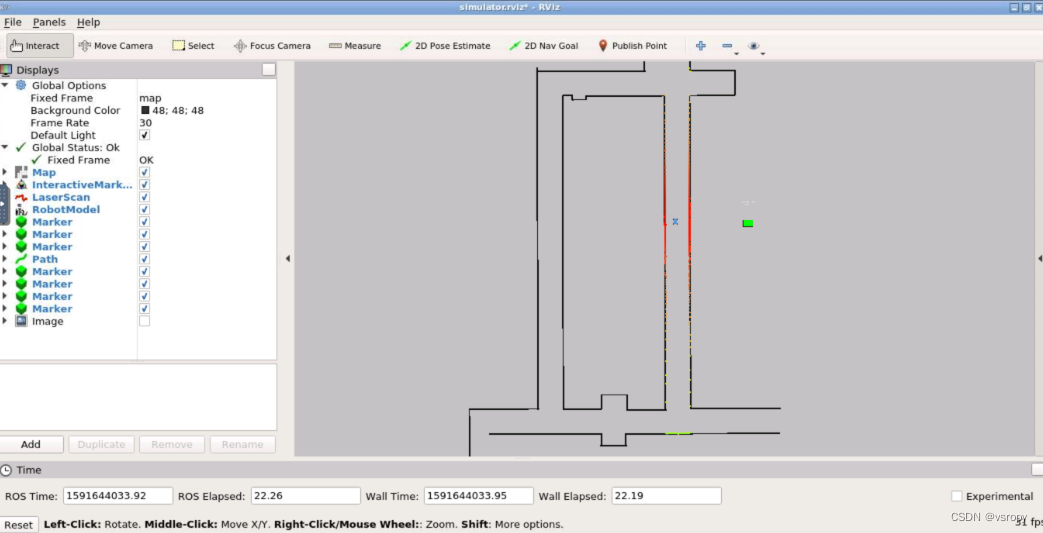
f1tenth仿真设置
文章目录 一、安装依赖二、进入工作空间克隆三、编译四、运行 一、安装依赖 tf2_geometry_msgs ackermann_msgs joy map_server sudo apt-get install ros-noetic-tf2-geometry-msgs ros-noetic-ackermann-msgs ros-melodic-joy ros-noetic-map-server 二、进入工作空间克隆…...

Technical debt (技术负债 / 技术债)
Technical debt (技术负债 / 技术债) In software development, or any other IT field (e.g., Infrastructure, Networking, etc.) technical debt (also known as design debt or code debt) is the implied cost of future reworking required when choosing an easy but li…...
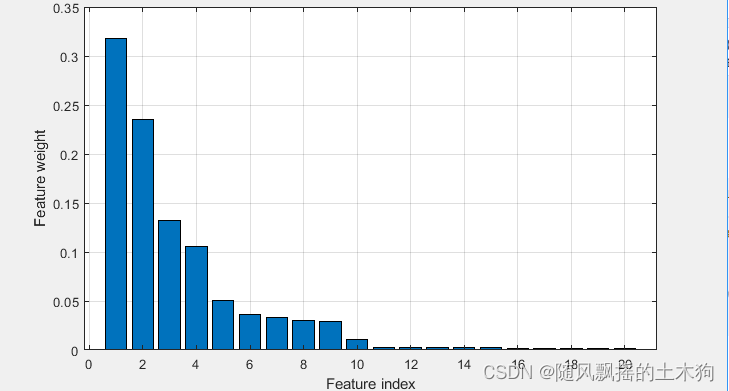
【MATLAB第67期】# 源码分享 | 基于MATLAB的morris全局敏感性分析
【MATLAB第67期】# 源码分享 | 基于MATLAB的morris全局敏感性分析 一、代码展示 clear all npoint100;%在分位数超空间中要采样的点数(计算次数iternpoint*(nfac1) nfac20;%研究函数的不确定因素数量 [mu, order] morris_sa1((x)test_function(x), nfac, npoint)for t1:size…...
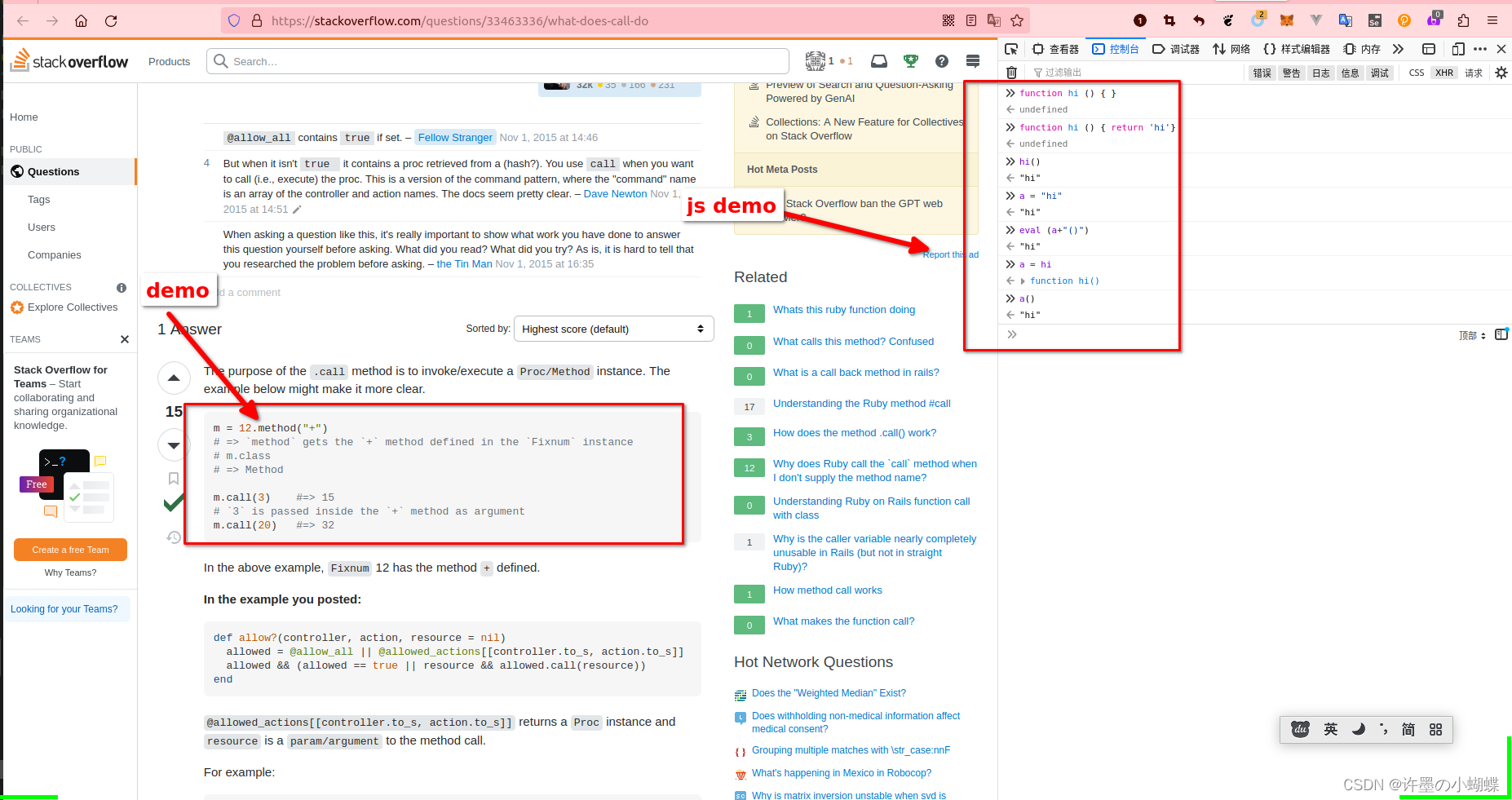
ruby send call 的简单使用
refer: ruby on rails - What does .call do? - Stack Overflow Ruby使用call 可以调用方法或者proc m 12.method("") # > method gets the method defined in the Fixnum instance # m.class # > Methodm.call(3) #> 15 # 3 is passed inside the…...

24聊城大学823软件工程考研
1.软件发展有几个阶段?各有何特征? ①程序设计阶段 硬件特征:价格贵、存储容量小、运行可靠性差。 软件特征:只有程序、程序设计概念,不重视程序设计方法。 ②程序系统阶段。 硬件特征:速度、容量及工作可…...
勘探开发人工智能技术:机器学习(3)
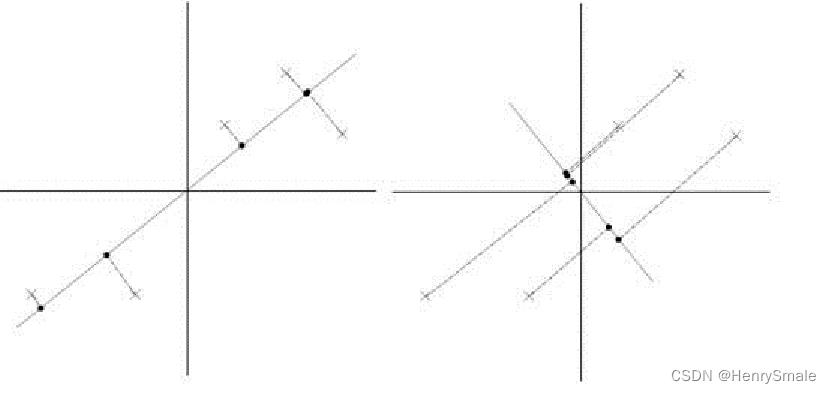
0 提纲 4.1 logistic回归 4.2 支持向量机(SVM) 4.3 PCA 1 logistic回归 用超平面分割正负样本, 考虑所有样本导致的损失. 1.1 线性分类器 logistic 回归是使用超平面将空间分开, 一边是正样本, 另一边是负样本. 因此, 它是一个线性分类器. 如图所示, 若干样本由两个特征描…...

定制 ChatGPT 以满足您的需求 自定义说明
推荐:使用 NSDT场景编辑器 快速助你搭建可二次编辑的3D应用场景 20 月 <> 日,OpenAI 宣布他们正在引入带有自定义说明的新流程,以根据您的特定需求定制 ChatGPT。 什么是自定义说明? 新的测试版自定义指令功能旨在通过防止…...

taro h5列表拖拽排序 --- sortablejs 和 react-sortable-hoc
描述:列表,拖拽排序,只测试了h5 一、sortablejs 文档:http://www.sortablejs.com/ 1.安装sortablejs 2、引入 import Sortable from sortablejs3、页面 const [list, setList] useState([{id: item-1,content: 选项1 }, {id…...
Linux的shell脚本常用命令
1、前提 使用shell脚本可以将所要执行的命令行进行汇总,统一执行,制作为脚本工具,简化重复性工作 1.1、常用命令 1.1.1、启动命令 假设我们拥有一个halloWord.sh的脚本,通过cd 命令进入相对应的目录下 ./halloWord.sh1.1.2、…...

使用自己的数据集预加载 Elasticsearch
作者:David Pilato 我最近在讨论论坛上收到一个问题,关于如何修改官方 Docker 镜像以提供一个现成的 Elasticsearch 集群,其中已经包含一些数据。 说实话,我不喜欢这个想法,因为你必须通过提 entrypoint.sh 的分叉版本…...

机器视觉赛道持续火热,深眸科技坚持工业AI视觉切入更多应用领域
随着深度学习等算法的突破、算力的不断提升以及海量数据的持续积累,人工智能逐渐从学术界向工业界落地。而机器视觉作为人工智能领域中一个正在快速发展的分支,广泛应用于工业制造的识别、检测、测量、定位等场景,相较于人眼,在精…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

USB Over IP专用硬件的5个特点
USB over IP技术通过将USB协议数据封装在标准TCP/IP网络数据包中,从根本上改变了USB连接。这允许客户端通过局域网或广域网远程访问和控制物理连接到服务器的USB设备(如专用硬件设备),从而消除了直接物理连接的需要。USB over IP的…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

scikit-learn机器学习
# 同时添加如下代码, 这样每次环境(kernel)启动的时候只要运行下方代码即可: # Also add the following code, # so that every time the environment (kernel) starts, # just run the following code: import sys sys.path.append(/home/aistudio/external-libraries)机…...
