【MATLAB第67期】# 源码分享 | 基于MATLAB的morris全局敏感性分析
【MATLAB第67期】# 源码分享 | 基于MATLAB的morris全局敏感性分析
一、代码展示
clear all
npoint=100;%在分位数超空间中要采样的点数(计算次数iter=npoint*(nfac+1)
nfac=20;%研究函数的不确定因素数量
[mu, order] = morris_sa1(@(x)test_function(x), nfac, npoint)for t=1:size(mu,2)
W(1,t)=mu(1,t)/sum(mu);
end
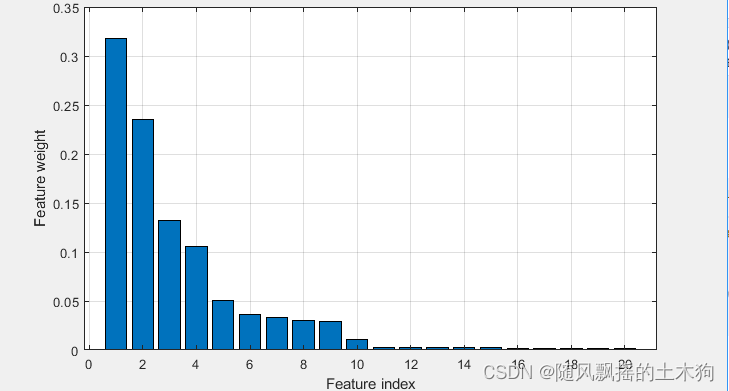
figure()
bar(W)
grid on
xlabel('Feature index')
ylabel('Feature weight')%输出
%1)μ:
%每个因素,按降序排列。
%2)order:各因素的指标。考虑修正最后的因素,
%那些“mu”非常接近于零的数。function [ mu, order ] = morris_sa1( studied_function, nfac, npoint )%
%输出
%1)μ:
%每个因素,按降序排列。
%2)顺序:各因素的指标。考虑修正最后的因素,
%那些“mu”非常接近于零的人。
delta=1/npoint;
mini=delta/2;
maxi=mini+delta*(npoint-1);coord = 0:npoint-1;
for i=1:nfacpoints(1:npoint,i) = coord(randperm(length(coord)));
end
points = points/(npoint-1)*(maxi-mini)+mini;for i=1:npointtable_outputs(i,1) = studied_function(points(i,:)); % Output at the sampled point.for j=1:nfacif points(i,j) < 0.5 % If the coordinate is smaller than 0.5, a positive variation is appliedtable_outputs(i,1+j) = studied_function([points(i,1:j-1) points(i,j)+0.5 points(i,j+1:nfac)]); % Output after the variation of the j-th factor.table_ee(i,j) = (table_outputs(i,1+j)-table_outputs(i,1))/0.5; % Elementary effect of the j-th factor.else % If the coordinate if larger than 0.5, a negative variation is appliedtable_outputs(i,1+j) = studied_function([points(i,1:j-1) points(i,j)-0.5 points(i,j+1:nfac)]);table_ee(i,j) = (table_outputs(i,1+j)-table_outputs(i,1))/(-0.5);endend
end% Estimation of the factors influence with the average of the absolute
% values of the elementary effects
for j=1:nfacmu_temp(j) = mean(abs(table_ee(:,j)));
end[mu, order] = sort(mu_temp,'descend'); % Ordering.end
目标函数
a = [100 0 100 100 100 100 1 10 0 0 9 0 100 100 4 100 100 7 100 2];
alpha = [1 4 1 1 1 1 0.4 3 0.8 0.7 2 1.3 1 1 0.3 1 1 1.5 1 0.6];
delt = [0.2942 0.2560 0.3004 0.5150 0.7723 0.4567 0.8390 0.1369 0.1558 0.4356 0.0257 0.3248 0.0718 0.9155 0.6877 0.5548 0.5835 0.8083 0.6309 0.8071];for i=1:20y(i) = ((1+alpha(i))*abs(2*(X(i)+delt(i)-fix(X(i)+delt(i)))-1)^alpha(i)+a(i))/(1+a(i));
end
二、效果展示
三、代码获取
后台私信回复“67期”即可获取下载链接。
相关文章:

【MATLAB第67期】# 源码分享 | 基于MATLAB的morris全局敏感性分析
【MATLAB第67期】# 源码分享 | 基于MATLAB的morris全局敏感性分析 一、代码展示 clear all npoint100;%在分位数超空间中要采样的点数(计算次数iternpoint*(nfac1) nfac20;%研究函数的不确定因素数量 [mu, order] morris_sa1((x)test_function(x), nfac, npoint)for t1:size…...
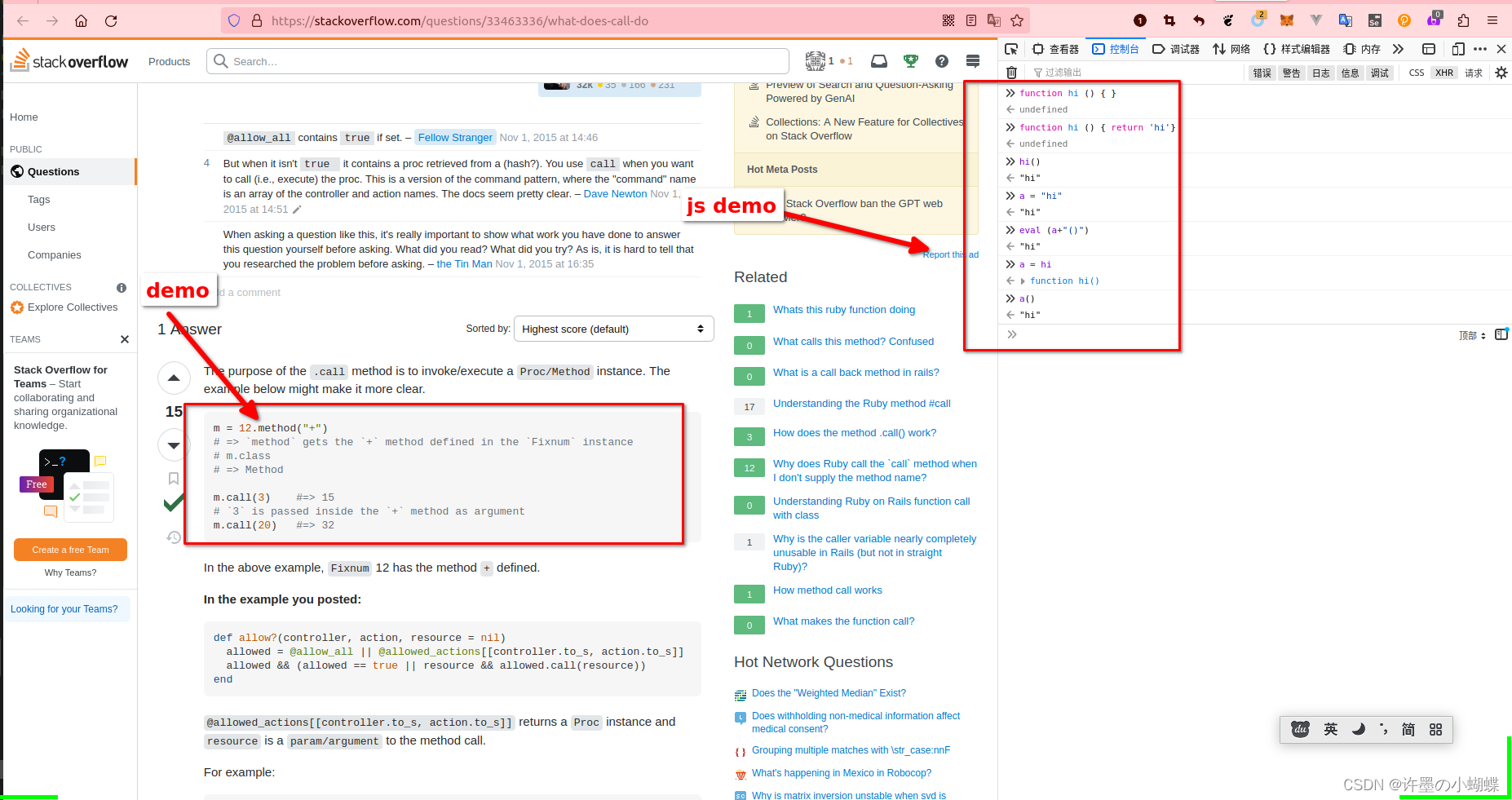
ruby send call 的简单使用
refer: ruby on rails - What does .call do? - Stack Overflow Ruby使用call 可以调用方法或者proc m 12.method("") # > method gets the method defined in the Fixnum instance # m.class # > Methodm.call(3) #> 15 # 3 is passed inside the…...

24聊城大学823软件工程考研
1.软件发展有几个阶段?各有何特征? ①程序设计阶段 硬件特征:价格贵、存储容量小、运行可靠性差。 软件特征:只有程序、程序设计概念,不重视程序设计方法。 ②程序系统阶段。 硬件特征:速度、容量及工作可…...
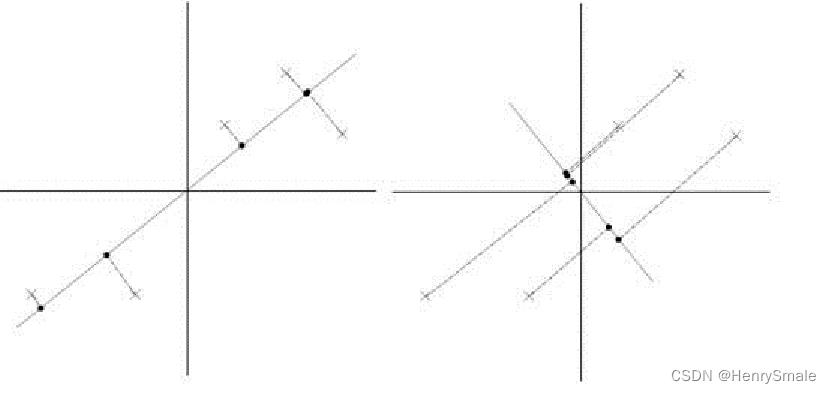
勘探开发人工智能技术:机器学习(3)
0 提纲 4.1 logistic回归 4.2 支持向量机(SVM) 4.3 PCA 1 logistic回归 用超平面分割正负样本, 考虑所有样本导致的损失. 1.1 线性分类器 logistic 回归是使用超平面将空间分开, 一边是正样本, 另一边是负样本. 因此, 它是一个线性分类器. 如图所示, 若干样本由两个特征描…...

定制 ChatGPT 以满足您的需求 自定义说明
推荐:使用 NSDT场景编辑器 快速助你搭建可二次编辑的3D应用场景 20 月 <> 日,OpenAI 宣布他们正在引入带有自定义说明的新流程,以根据您的特定需求定制 ChatGPT。 什么是自定义说明? 新的测试版自定义指令功能旨在通过防止…...

taro h5列表拖拽排序 --- sortablejs 和 react-sortable-hoc
描述:列表,拖拽排序,只测试了h5 一、sortablejs 文档:http://www.sortablejs.com/ 1.安装sortablejs 2、引入 import Sortable from sortablejs3、页面 const [list, setList] useState([{id: item-1,content: 选项1 }, {id…...
Linux的shell脚本常用命令
1、前提 使用shell脚本可以将所要执行的命令行进行汇总,统一执行,制作为脚本工具,简化重复性工作 1.1、常用命令 1.1.1、启动命令 假设我们拥有一个halloWord.sh的脚本,通过cd 命令进入相对应的目录下 ./halloWord.sh1.1.2、…...

使用自己的数据集预加载 Elasticsearch
作者:David Pilato 我最近在讨论论坛上收到一个问题,关于如何修改官方 Docker 镜像以提供一个现成的 Elasticsearch 集群,其中已经包含一些数据。 说实话,我不喜欢这个想法,因为你必须通过提 entrypoint.sh 的分叉版本…...

机器视觉赛道持续火热,深眸科技坚持工业AI视觉切入更多应用领域
随着深度学习等算法的突破、算力的不断提升以及海量数据的持续积累,人工智能逐渐从学术界向工业界落地。而机器视觉作为人工智能领域中一个正在快速发展的分支,广泛应用于工业制造的识别、检测、测量、定位等场景,相较于人眼,在精…...
MyBatis操作数据库常见用法总结2
文章目录 1.动态SQL使用什么是动态sql为什么用动态sql标签拼接标签拼接标签拼接标签拼接标签拼接 补充1:resultType和resultMap补充2:后端开发中单元测试工具使用(Junit框架) 1.动态SQL使用 以insert标签为例 什么是动态sql 是…...
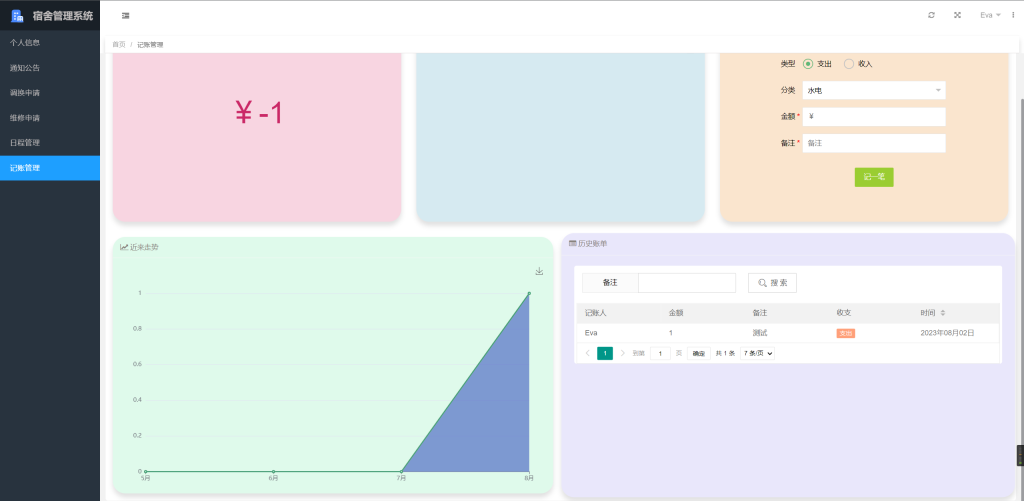
基于SpringBoot+LayUI的宿舍管理系统 001
项目简介 源码来源于网络,项目文档仅用于参考,请自行二次完善哦。 系统以MySQL 8.0.23为数据库,在Spring Boot SpringMVC MyBatis Layui框架下基于B/S架构设计开发而成。 系统中的用户分为三类,分别为学生、宿管、后勤。这三…...
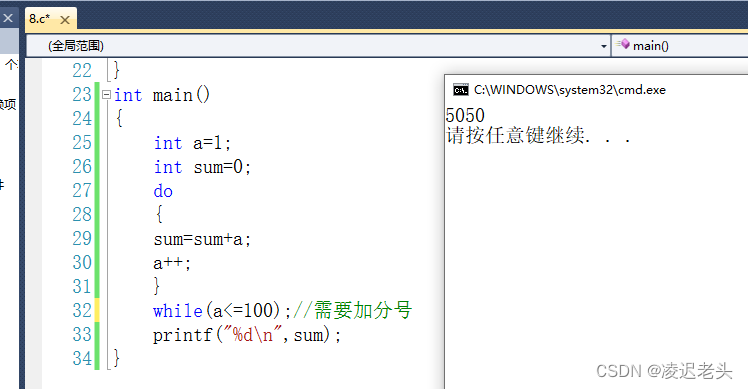
C语言笔记7
#include <stdio.h> int main(void) {int a123;int b052;//十进制42int c0xa2;//十进制162printf("a%d b%o c%x \n",a,b,c);//分别是十进制 八进制 十六进制printf("a%d b%d c%d \n",a,b,c);printf("Hello 凌迟老头\n");return …...

Centos更换网卡名称为eth0
Centos更换网卡名称为eth0 已安装好系统后需要修改网卡名称为eth0 编辑配置文件将ens33信息替换为eth0,可在vim命令模式输入%s/ens33/eth0/g替换相关内容 修改内核文件,添加内容:net.ifnames=0 biosdevname=0 [root@nova3 ~]# vim /etc/default/grub 使用命令重新生成g…...

【Express.js】软件测试
软件测试 本节介绍如何在 express.js 使用 Jest 进行单元测试 准备工作 准备一个基础的 express 项目,本文基于 evp-express-cli安装 Jest npm install jest --save-dev生成 Jest 配置 npx jest --init编写测试 创建测试文件,以 .test.js 后缀命名…...

TCP三次握手、四次握手过程,以及原因分析
TCP的三次握手和四次挥手实质就是TCP通信的连接和断开。 三次握手:为了对每次发送的数据量进行跟踪与协商,确保数据段的发送和接收同步,根据所接收到的数据量而确认数据发送、接收完毕后何时撤消联系,并建立虚连接。 四次挥手&…...

OceanBase X Flink 基于原生分布式数据库构建实时计算解决方案
摘要:本文整理自 OceanBase 架构师周跃跃,在 Flink Forward Asia 2022 实时湖仓专场的分享。本篇内容主要分为四个部分: 分布式数据库 OceanBase 关键技术解读 生态对接以及典型应用场景 OceanBase X Flink 在游戏行业实践 未来展望 点击…...

600V EasyPIM™ IGBT模块FB30R06W1E3、FB20R06W1E3B11、FB20R06W1E3降低了系统成本和损耗,可满足高能效要求。
EasyPIM™ IGBT模块是一种三相输入整流器PIM IGBT模块,采用TRENCHSTOP™ IGBT7、发射器控制7二极管和NTC/PressFIT技术。该模块具有增强的dv/dt可控性、改进的FWD软度、优化的开关损耗以及8μs短路稳定性。EasyPIM(功率集成模块)外形非常小巧…...
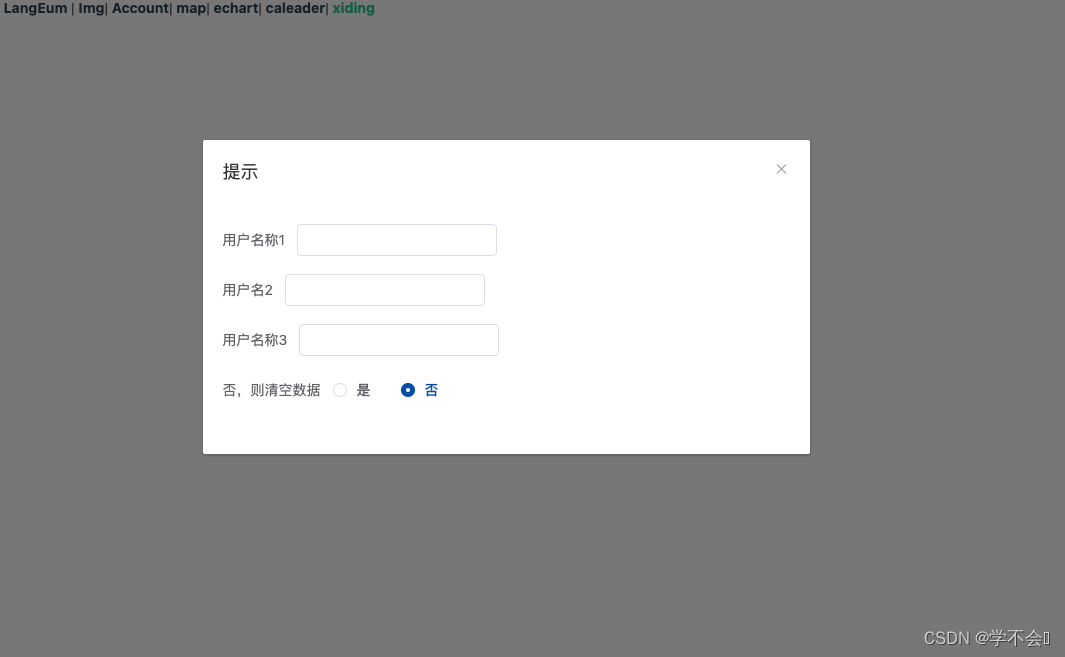
form 表单恢复初始数据
写表单的时候,想做到,某个操作时,表单恢复初始数据 this.$options.data().form form 是表单的对象 <template><div><el-dialog title"提示" :visible.sync"dialogVisible"><el-form :model"…...

MySQL—索引
这里写目录标题 索引是什么? 索引优缺点?MySQL索引类型索引底层实现? 为什么使用B树, 而不是B树, BST, AVL, 红黑树等等?什么是聚簇索引和非聚簇索引?非聚簇索引一定会回表吗?什么是联合索引?为什么需要注意联合索引中的字段顺序?什么是最左前缀原则?什么是前缀索引?…...

Android图形-合成与显示-概论
目录 引言 概念与理解 SurfaceFlinger Surface HWC Fence: Gralloc: DisplayDevice 引言 Activity是Android的主要UI相关组件。通过View的相关类和接口实现,在WMS的管理下,进行窗口和控件的测量,布局和绘制&am…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...

STM32HAL库USART源代码解析及应用
STM32HAL库USART源代码解析 前言STM32CubeIDE配置串口USART和UART的选择使用模式参数设置GPIO配置DMA配置中断配置硬件流控制使能生成代码解析和使用方法串口初始化__UART_HandleTypeDef结构体浅析HAL库代码实际使用方法使用轮询方式发送使用轮询方式接收使用中断方式发送使用中…...
