数据结构--栈和队列3.1(栈-顺序结构)
目录
栈(Stack)栈顶(top)栈底(bottom)空栈(不含任何元素)
创建栈
入栈操作
出栈操作
销毁一个栈
计算栈的当前容量
实例分析
栈的插入操作叫做进栈(Push),或者称为压栈、入栈。
栈的删除操作叫做出栈(Pop),或者称为弹栈。
栈又称为先进后出(last in first out)的后进先出原则,称为后进先出的线性表(LIFO)。
栈的本质上也是一个线性表,线性表有两种存储形式,那么栈也有分为栈的顺序存储结构和栈的链式存储结构。
最开始栈中不含有任何数据,叫做空栈,此时栈定就是栈底。然后数据从栈顶进入,栈顶栈底分离,整个栈的当前容量变大。数据出栈时,从栈顶移出,栈顶下一,整个栈的当前容量变小。
栈的顺序存储结构:
typedef struct
{ElemType *base;ElemType *top;int stacksize;}sqStack;这里定义了一个顺序存储的栈,它包含了三个元素:base,top,stacksize。其中base是指向栈底的指针变量,top是指向栈顶的指针变量,stacksize指示栈的当前可使用的最大容量。
创建栈
#define STACK_INIT_SIZE 100 initStack(sqStack *s)//创建栈
{s->base = (ElemType *)malloc(STACK_INIT_SIZE * sizeof(ElemType));if(!s->base)exit(0);s->top=s->base; //最开始,栈顶就是栈底。 s->stacksize = STACK_INIT_SIZE;} 入栈操作
#include <stdlib.h>
#define STACKINCREMENT 10Push(sqStack *s,ElemType e) //入栈操作
{if(s->top - s->base >= s->stacksize){//如果漫展,追加空间 s->base = (ElemType *)realloc(s->base,(s->stacksize+STACKINCREMENT)*sizeof(ElemType));if(!s->base)exit(0);s->top=s->base + s->stacksize;s->stacksize = s->stacksize + STACKINCREMENT;}*(s-top)=e;s->top++; } 出栈操作
出栈操作就是在栈顶取出数据,栈顶指针随之下移的操作。
每当从栈内弹出一个数据,栈的当前容量就-1.
Pop(sqStack *s,ElemType *e)
{if(s->top==s->base)//栈已空return;*e=*--(s->top);
}销毁一个栈
DestrogStack(sqStack *s)
{int i,len;len = s->stackSize;for(i=0;i<len;i++){free(s->base);s->base++;}s->base = s->top =NULL;s->stacksize = 0;
}计算栈的当前容量
计算栈的当前容量也就是计算栈中元素的个数,因此只要返回s.top-s.base 即可。
栈的最大容量是指该栈占据内存空间的大小,其值是s.stackSzie,它与栈的当前容量不是一个概念。
int StackLen(sqStack s)
{return (s.top-s.base+1);
}实例分析
利用栈的数据结构特点,将二进制转换为十进制数。
#include <stdio.h>
#include <stdlib.h>
#include <math.h>#define STACK_INIT_SIZE 20
#define STACKINCREMENT 10typedef char ElemType;
typedef struct
{ElemType *base;ElemType *top;int stackSize; }sqStack;void InitStack(sqStack *s)
{s->base = (ElemType *)malloc(STACK_INIT_SIZE * sizeof(ElemType));if(!s->base)exit(0);s->top = s->base;s->stackSize=STACK_INIT_SIZE;
}void Push(sqStack *s,ElemType e)
{if(s->top - s->base>= s->stackSize){s->base=(ElemType *)realloc(s->base,(s->stackSize+STACKINCREMENT) * sizeof(ElemType));if(!s->base){exit(0);}}*(s->top)=e;s->top++;} void Pop(sqStack *s,ElemType *e)
{if(s->top==s->base){return;}*e = *--(s->top);
}int StackLen(sqStack s)
{return (s.top- s.base);
}int main(void)
{ElemType c;sqStack s;int len ,i,sum=0;InitStack(&s);printf("请输入二进制数,输入#符号表示结束!");scanf("%c",&c);while(c!='#'){Push(&s,c);scanf("%c",&c);}getchar();len = StackLen(s);printf("栈的当前容量是:%d\n",len);for(i=0;i<len;i++){Pop(&s,&c);sum=sum+(c-48)*pow(2,i);}printf("%d",sum);return 0;
}相关文章:
)
数据结构--栈和队列3.1(栈-顺序结构)
目录 栈(Stack)栈顶(top)栈底(bottom)空栈(不含任何元素) 创建栈 入栈操作 出栈操作 销毁一个栈 计算栈的当前容量 实例分析 栈的插入操作叫做进栈(Push…...
pdf怎么压缩到1m?这样做压缩率高!
PDF是目前使用率比较高的一种文档格式,因为它具有很高的安全性,还易于传输等,但有时候当文件体积过大时,会给我们带来不便,这时候简单的解决方法就是将其压缩变小。 想要将PDF文件压缩到1M,也要根据具体的情…...

AttentionFreeTransformer 源码解析(一):AFTFull、AFTSimple、AFTLocal
我觉得源码写的很好懂,我就不加注释了,直接上计算流程图。 AFTFull class AFTFull(nn.Module):def __init__(self, max_seqlen, dim, hidden_dim64):super().__init__()max_seqlen: the maximum number of timesteps (sequence length) to be fed indim…...
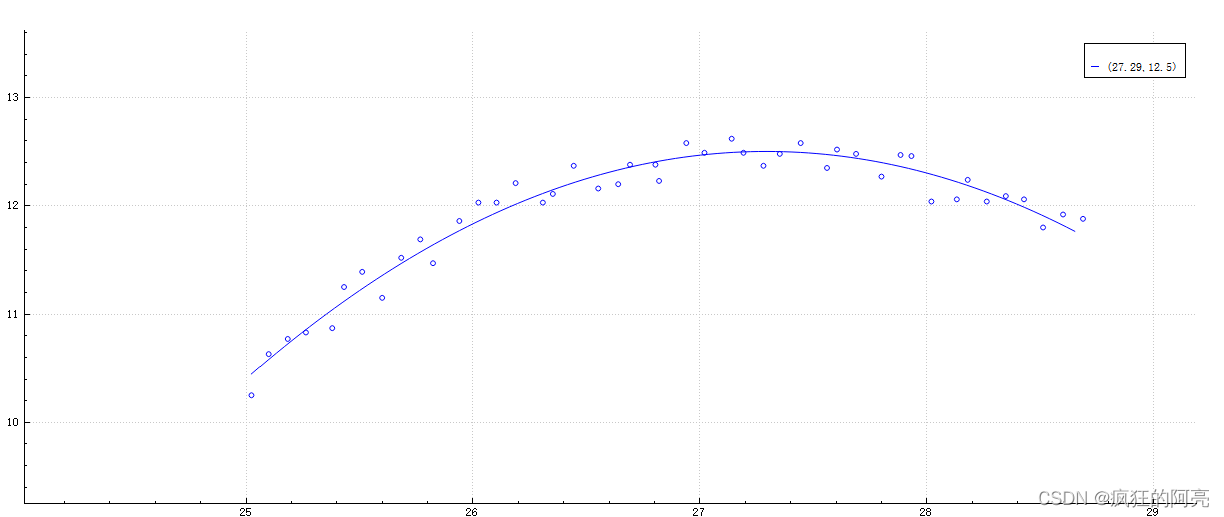
C++ 计算 拟合优度R^2
解决的问题: 拟合优度(Goodness of Fit)是指回归直线对观测值的拟合程度,度量拟合优度的统计量是可决系数(亦称确定系数) R?。R最大值为 1。R%的值越接近1,说明回归直线对观测值的拟合程度越好,反之,R%值越小&#x…...
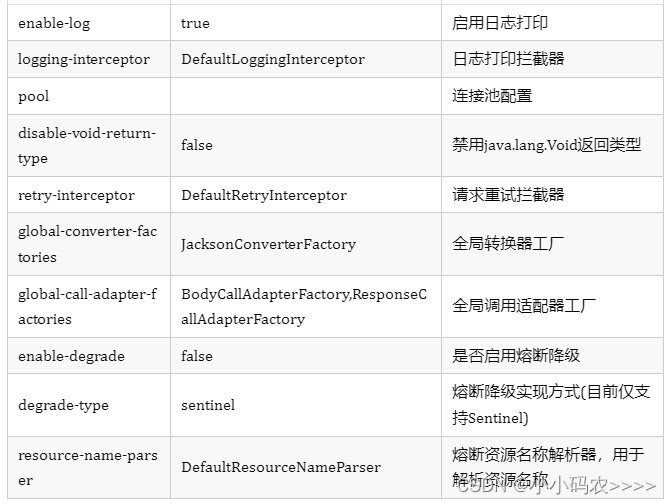
Springboot-Retrofit HTTP工具框架快速使用
在SpringBoot项目直接使用okhttp、httpClient或者RestTemplate发起HTTP请求,既繁琐又不方便统一管理。 因此,在这里推荐一个适用于SpringBoot项目的轻量级HTTP客户端框架retrofit-spring-boot-starter,使用非常简单方便,同时又提供…...
)
微信小程序实现人脸识别(从一个没有开通人脸核身的小程序跳转到要给开通人脸核身的小程序,进行人脸识别后再跳转回来)
A小程序没有开通人脸识别功能,B小程序开通了人脸识别。 总体思路是:从A小程序需要进行人脸识别的地方携带参数跳转到B小程序进行人脸识别,识别后把参数传递回来。 A小程序的参考代码如下: //人脸识别相关 start powerDrawerFace(e){var that = thisthat.setData({faceO…...
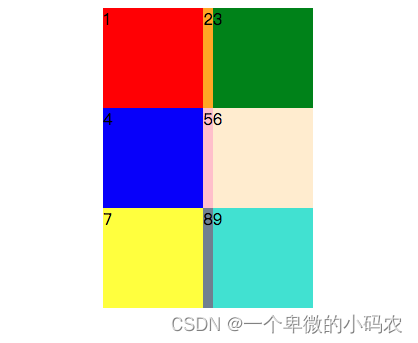
CSS-grid布局
网格布局也叫grid布局,平常写样式的时候基本上都是用的flex布局。 像以下布局,用flex布局就可能会有有点麻烦,这时候用grid布局就方便的多了。 或者是照片墙 grid布局就是将容器划分为行和列,产生单元格,然后在指定的…...
【JavaEE进阶】Bean 作用域和生命周期
文章目录 一. 关于Bean作用域的实例1. lombok2. 实例代码 二. 作用域定义1. Bean的六种作用域2. 设置作用域 三. Spring 执行流程和 Bean 的生命周期1. Spring 执行流程2. Bean生命周期 一. 关于Bean作用域的实例 注意在此例子中需要用到lombok 1. lombok lombok是什么? Lo…...
3分钟自建查分系统?现在每个人都可以实现了
学生成绩查询系统在现代教育管理中扮演着重要的角色,它不仅可以方便学生和家长查询成绩,也能帮助老师更好地管理和分析学生的学业表现。作为一名教师,了解如何制作学生成绩查询系统是提高教学效率和管理学生成绩便利性的关键。 在制作学生成…...

关于APP备案、小程序备案的问题,如何备案?
近日,工信部发布了关于开展移动互联网应用程序备案工作的通知。为落实相关法律法规要求,促进互联网行业规范健康发展,进一步做好移动互联网信息服务管理,现组织开展移动互联网应用程序(以下简称 APP)备案工…...

git上传代码后,如何清空历史日志以及文件操作,重新上传?以及上传代码
【Git教程】如何清除git仓库的所有提交记录,成为一个新的干净仓库 马三也算Github的忠实用户了,经常会把一些练手的项目传到Github上面进行备份。其中有一个名为ColaFramework的Unity框架项目,马三开发了一年多了,期间提交代码的…...

超导热催生meme,换汤不换药的投机轮回
文/章鱼哥 出品/陀螺财经 币圈对炒作meme概念的热情从未消亡过。 随着一种名为LK-99的物质被发现,围绕超导的兴奋不仅激发了科学界,加密货币相关概念也与之沸腾。不出所料,与此前围绕元宇宙、AI大肆炒作一样,许多meme代币已经出现…...

【HashMap】 73. 矩阵置零
73. 矩阵置零 解题思路 首先遍历矩阵找到所有的0元素 将其的行和列索引记录下俩遍历矩阵 将所有的需要更新的元素进行更新 也就是查找hashmap中的每一个元素进行更新查找行或者列是否在hashmap中 class Solution {public void setZeroes(int[][] matrix) {// 首先遍历矩阵找…...
Vue-2.nodejs的介绍和安装
nodejs简介 ► 创建 Node.js 应用:package.json 首先,创建一个新文件夹以便于容纳需要的所有文件,并且在此其中创建一个 package.json 文件,描述你应用程序以及需要的依赖: 配合着你的 package.json 请运行 npm install。如果你…...

分别用Vue和Java来实现的风靡一时的2048 游戏
目录 1、Vue实现2、Java实现 2048 游戏是一个基于网格的数字益智游戏,玩家需要通过滑动相同的数字来合并它们,并最终得到一个值为 2048 的方块。以下是分别用Vue和Java来实现的 2048 游戏,包含运行效果。 1、Vue实现 首先,创建一…...
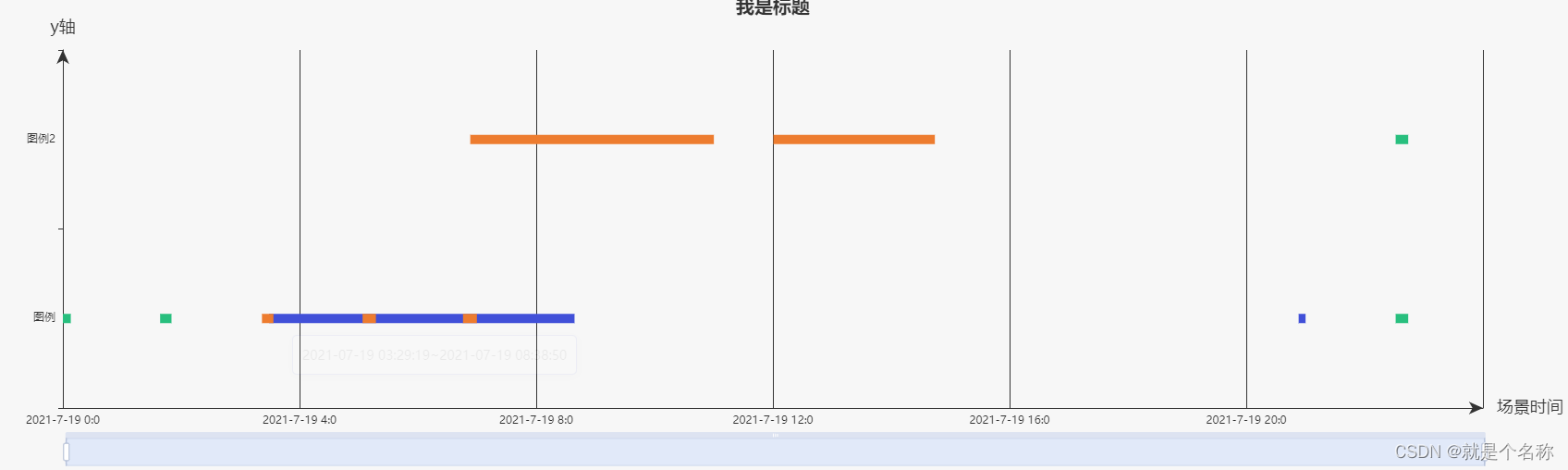
echarts甘特图 一个值多条线
先看图 这里我们用到的是 series :type:custom 自定义,但是这里我遇到一个问题,就是不过你在series里push多少数据,图表上显示的都是在同一水平线,用了好多方法都不好使, renderItem: (params, api) >…...

多态性说明
多态 多态性多态性类型描述编译时多态和运行时多态的差异go 语言多态性 多态性 多态性类型描述 多态性是面向对象编程中的一个重要概念,它允许不同的对象通过相同的接口表现出不同的行为,从而实现更加灵活和可扩展的代码结构。多态性有助于降低代码的耦…...

2023-08-04 LeetCode每日一题(不同路径 III)
2023-08-04每日一题 一、题目编号 980. 不同路径 III二、题目链接 点击跳转到题目位置 三、题目描述 在二维网格 grid 上,有 4 种类型的方格: 1 表示起始方格。且只有一个起始方格。2 表示结束方格,且只有一个结束方格。0 表示我们可以…...

腾讯云服务器地域怎么选?可用区是什么?
腾讯云服务器地域有什么区别?怎么选择比较好?地域选择就近原则,距离地域越近网络延迟越低,速度越快。关于地域的选择还有很多因素,地域节点选择还要考虑到网络延迟速度方面、内网连接、是否需要备案、不同地域价格因素…...
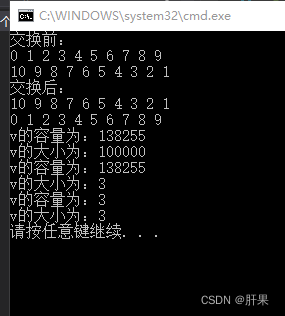
第一百二十三天学习记录:C++提高:STL-vector容器(下)(黑马教学视频)
vector插入和删除 功能描述: 对vector容器进行插入、删除操作 函数原型: push_back(ele); //尾部插入元素ele pop_back(); //删除最后一个元素 insert(const_iterator pos, ele); //迭代器指向位置pos插入元素ele insert(const_iterator pos, int cou…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...
