opencv基础46-图像金字塔02-拉普拉斯金字塔
前面我们介绍了高斯金字塔,高斯金字塔是通过对一幅图像一系列的向下采样所产生的。有时,我们希望通过对金字塔中的小图像进行向上采样以获取完整的大尺寸高分辨率图像,这时就需要用到拉普拉斯金字塔
前面我们已经介绍过,一幅图像在经过向下采样后,再对其进行向上采样,是无法恢复为原始状态的。对此,我们也用程序进行了验证。向上采样并不是向下采样的逆运算。这是很明显的,因为向下采样时在使用高斯滤波器处理后还要抛弃偶数行和偶数列,不可避免地要丢失一些信息。
为了在向上采样时能够恢复具有较高分辨率的原始图像,就要获取在采样过程中所丢失的信息,这些丢失的信息就构成了拉普拉斯金字塔。
拉普拉斯金字塔的定义形式为:
Li = Gi - pyrUp(Gi + 1)
式中:
- Li表示拉普拉斯金字塔中的第 i 层。
- Gi表示高斯金字塔中的第 i 层。
拉普拉斯金字塔中的第 i 层,等于“高斯金字塔中的第 i 层”与“高斯金字塔中的第 i+1 层的向上采样结果”之差。图 11-11 展示了高斯金字塔和拉普拉斯金字塔的对应关系。
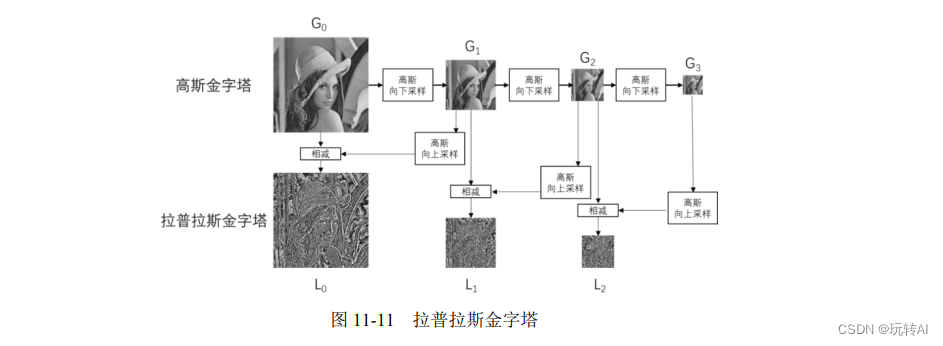
代码示例:使用函数 cv2.pyrDown()和 cv2.pyrUp()构造拉普拉斯金字塔。
import cv2
O=cv2.imread("lena.png")
G0=O
G1=cv2.pyrDown(G0)
G2=cv2.pyrDown(G1)
G3=cv2.pyrDown(G2)
L0=G0-cv2.pyrUp(G1)
L1=G1-cv2.pyrUp(G2)
L2=G2-cv2.pyrUp(G3)
print("L0.shape=",L0.shape)
print("L1.shape=",L1.shape)
print("L2.shape=",L2.shape)
cv2.imshow("L0",L0)
cv2.imshow("L1",L1)
cv2.imshow("L2",L2)
cv2.waitKey()
cv2.destroyAllWindows()
程序运行后,会输出如下运行结果:
L0.shape= (512, 512, 3)
L1.shape= (256, 256, 3)
L2.shape= (128, 128, 3)
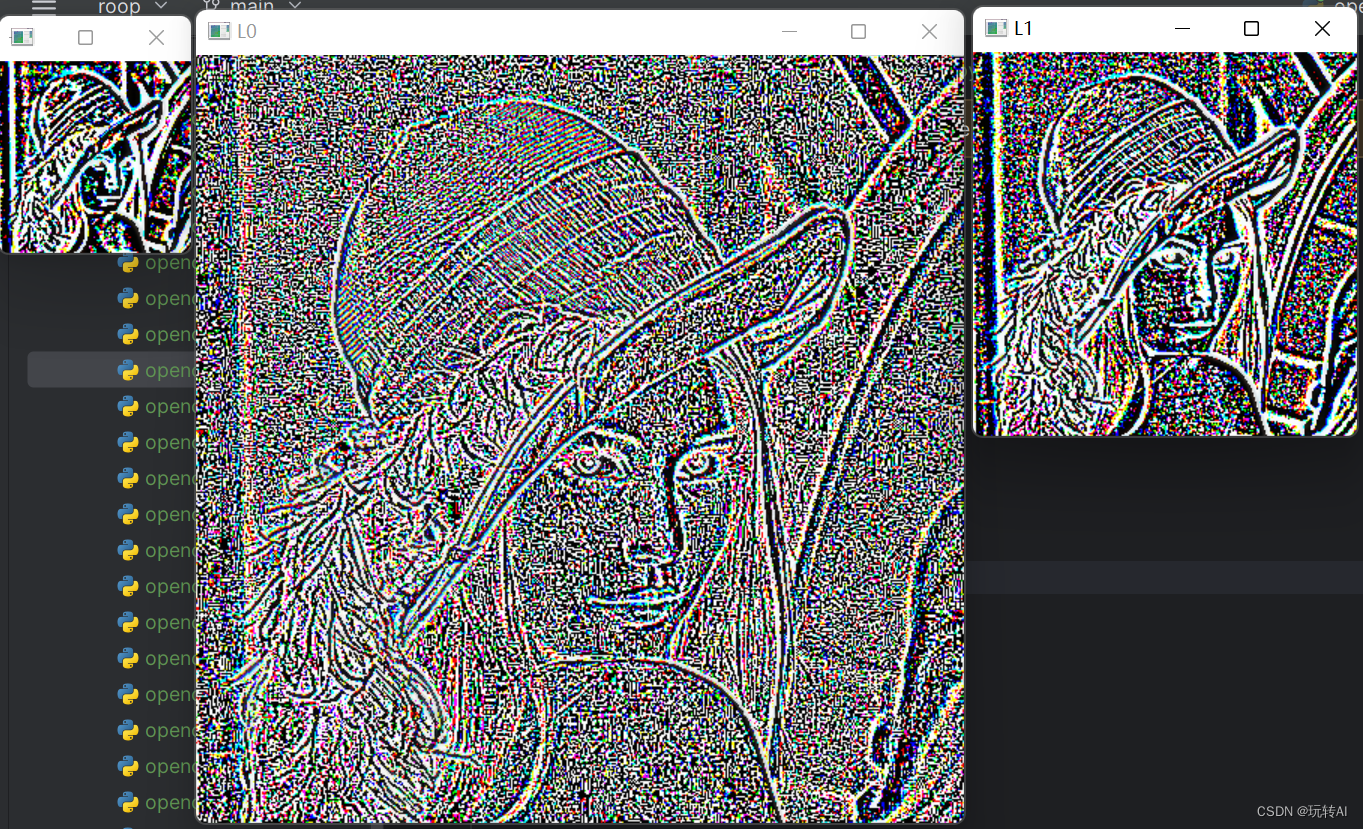
1 中图是通过语句“L0=G0-cv2.pyrUp(G1)”,用“原始图像 G0”减去“图像 G1 的向上
采样结果”,得到的拉普拉斯金字塔的第 0 层 L0。
右边图是通过语句“L1=G1-cv2.pyrUp(G2)”,用“图像 G1”减去“图像 G2 的向上采样
结果”,得到的拉普拉斯金字塔的第 1 层 L1。
左边小图是通过语句“L2=G2-cv2.pyrUp(G3)”,用“图像 G2”减去“图像 G3 的向上采样
结果”,得到的拉普拉斯金字塔的第 2 层 L2。
如何恢复原图?
拉普拉斯金字塔的作用在于,能够恢复高分辨率的图像。图 11-13 演示了如何通过拉普拉斯金字塔恢复高分辨率图像。其中,右图是对左图的简化。
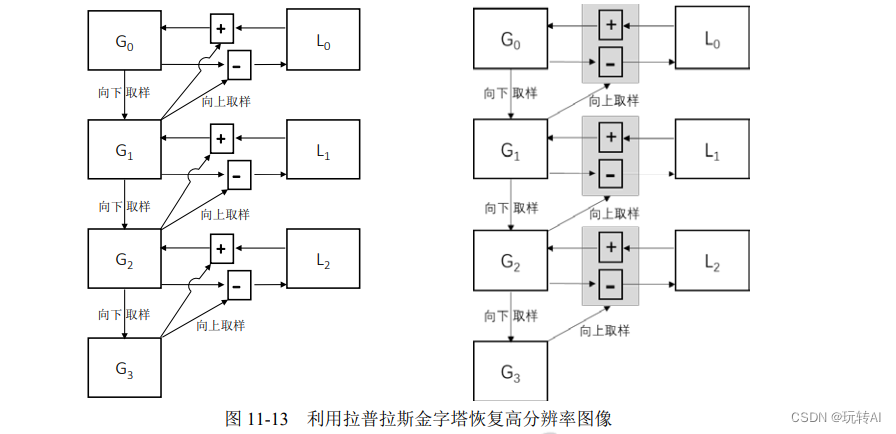
图 11-13 中的各个标记的含义如下:
- G0、G1、G2、G3分别是高斯金字塔的第 0 层、第 1 层、第 2 层、第 3 层。
- L0、L1、L2分别是拉普拉斯金字塔的第 0 层、第 1 层、第 2 层。
- 向下的箭头表示向下采样操作(对应 cv2.pyrDown()函数)。
- 向右上方的箭头表示向上采样操作(对应 cv2.pyrUp()函数)。
- 加号“+”表示加法操作。
- 减号“-”表示减法操作。
在图 11-13 中,描述的操作及关系有:
- 向下采样(高斯金字塔的构成)
G1=cv2.pyrDown(G0)
G2=cv2.pyrDown(G1)
G3=cv2.pyrDown(G2)
- 拉普拉斯金字塔
L0=G0-cv2.pyrUp(G1)
L1=G1-cv2.pyrUp(G2)
L2=G2-cv2.pyrUp(G3)
- 向上采样恢复高分辨率图像
G0=L0+cv2.pyrUp(G1)
G1=L1+cv2.pyrUp(G2)
G2=L2+cv2.pyrUp(G3)
上述关系是通过数学运算推导得到的。例如,已知L0=G0cv2.pyrUp(G1),将表达式右侧的 cv2.pyrUp(G1)移到左侧,就得到了表达式 G0=L0+cv2.pyrUp(G1)。除此之外,G1 和 G2 都可以通过拉普拉斯金字塔的构造表达式得到。在前面已经介绍过了,构造拉普拉斯金字塔的目的就是为了恢复高分辨率的图像。
代码示例:
import cv2
import numpy as np
O=cv2.imread("lena.png")
#==============生成高斯金字塔===================
G0=O
G1=cv2.pyrDown(G0)
G2=cv2.pyrDown(G1)
G3=cv2.pyrDown(G2)
#============生成拉普拉斯金字塔===================
L0=G0-cv2.pyrUp(G1) #拉普拉斯金字塔第 0 层
L1=G1-cv2.pyrUp(G2) #拉普拉斯金字塔第 1 层
L2=G2-cv2.pyrUp(G3) #拉普拉斯金字塔第 2 层
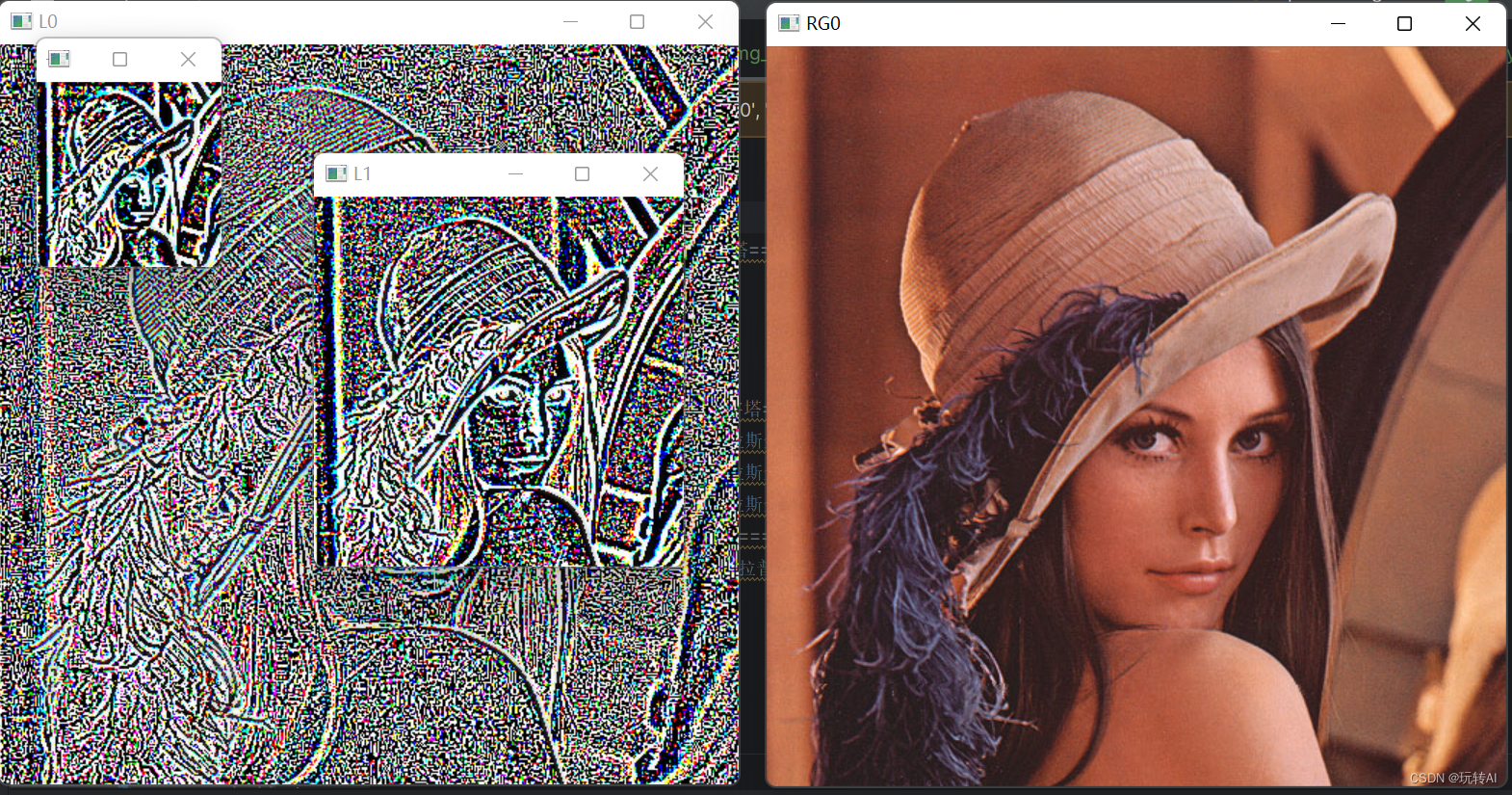
#=================复原 G0======================
RG0=L0+cv2.pyrUp(G1) #通过拉普拉斯图像复原的原始图像 G0cv2.imshow("L0",L0)
cv2.imshow("L1",L1)
cv2.imshow("L2",L2)
cv2.imshow("RG0",RG0)
cv2.waitKey()
cv2.destroyAllWindows()
相关文章:

opencv基础46-图像金字塔02-拉普拉斯金字塔
前面我们介绍了高斯金字塔,高斯金字塔是通过对一幅图像一系列的向下采样所产生的。有时,我们希望通过对金字塔中的小图像进行向上采样以获取完整的大尺寸高分辨率图像,这时就需要用到拉普拉斯金字塔 前面我们已经介绍过,一幅图像在…...
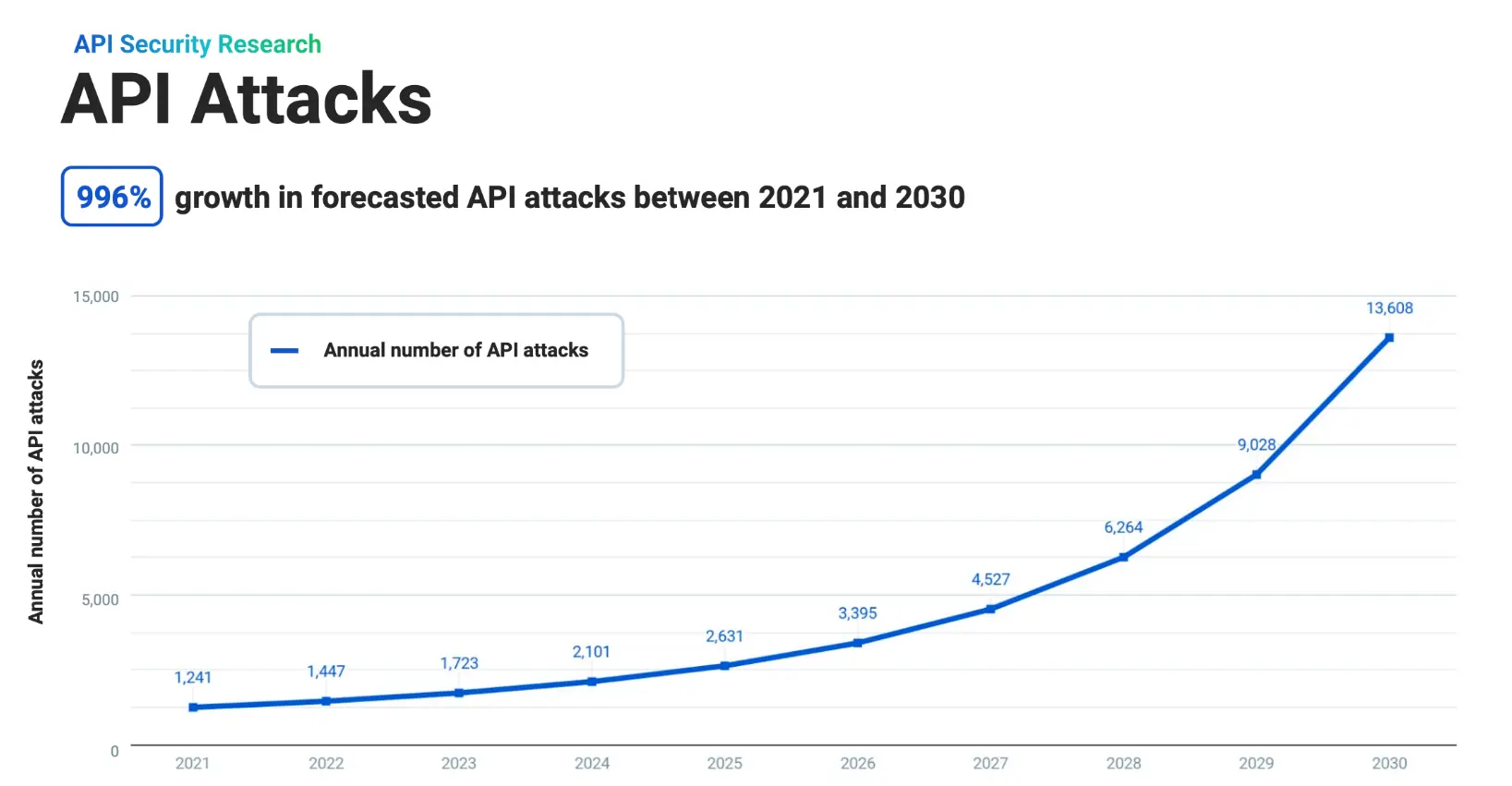
到 2030 年API 攻击预计将激增近 1000%
导读云原生应用程序编程接口管理公司 Kong 联合外部经济学家的最新研究预计,截至 2030 年 API 攻击将激增 996%,意味着与 API 相关的网络威胁的频率和强度都显着升级。 这项研究由 Kong 分析师和布朗大学副教授 Christopher Whaley 博士合作进行&#x…...

环形队列+DMA空闲中断+接收串口数据
环形队列DMA空闲中断接收串口数据 一.序言二.实验原理三.实战是检验真理的唯一标准3.1 usart1.c3.2 串口中断 三.队列代码4.1 fifo.c4.2 fifo.h 五.结语 一.序言 本次实验利用环形队列DMA空闲中断串口。。通过这个实验可以非常深入的理解队列,DMA,串口的知识。如果…...

LeetCode 31题:下一个排列
目录 题目 思路 代码 题目 整数数组的一个 排列 就是将其所有成员以序列或线性顺序排列。 例如,arr [1,2,3] ,以下这些都可以视作 arr 的排列:[1,2,3]、[1,3,2]、[3,1,2]、[2,3,1] 。 整数数组的 下一个排列 是指其整数的下一个字典序…...
CMake:检测python模块和包
CMake:检测python模块和包 导言项目结构CMakeLists.txt相关源码 导言 上一篇,我们基本了解了如何去检测python的解释器和python库。通常,代码是依赖于特定的python模块,无论是python工具、嵌入python的程序,还是扩展python的库。…...
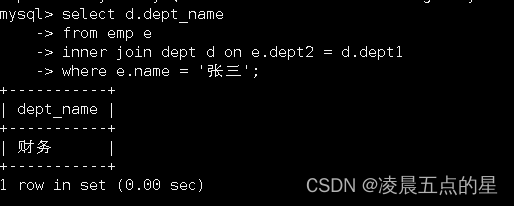
02Mysql之多表查询--例题讲解
一、题目详情,以及表的建立 新增员工表emp和部门表deptcreate table dept (dept1 int ,dept_name varchar(11));create table emp (sid int ,name varchar(11),age int,worktime_start date,incoming int,dept2 int);insert into dept values(101,财务),(102,销售)…...

虹科方案 | 汽车总线协议转换解决方案
汽车总线: 汽车总线是一种用于在车辆电子系统中传输数据和控制信息的通信系统。它允许不同的电子控制单元(ECU)在车辆中相互通信,协调各个系统的操作,以实现功能的集成和协同工作。 在现代汽车中,综合通信…...
Mr. Cappuccino的第59杯咖啡——简单手写SpringIOC框架
简单手写SpringIOC框架 环境搭建基于XML方式项目结构项目代码运行结果 基于注解方式项目结构项目代码运行结果 简单手写SpringIOC框架核心原理基于XML方式原理项目结构项目代码运行结果 基于注解方式原理项目结构项目代码运行结果 环境搭建 基于XML方式 项目结构 项目代码 p…...

爬虫 学习HTML标签和元素的基本概念,了解网页的结构和内容
HTML(Hypertext Markup Language)是一种用于创建网页的标记语言,由一系列的标签组成。标签使用尖括号(< 和 >)包围,并且通常成对出现,一个是开始标签,一个是结束标签。 HTML文…...

mysql将id重新修改为递增
文章目录 场景解决,排序的话可以先按照一定大小改一下,然后将id字段删掉,再重新生成即可清空表数据,并将自增id改为1开始 场景 好比我有个配置表: CREATE TABLE config (id int NOT NULL AUTO_INCREMENT,config_key varchar(20) NOT NULL,config_value varchar(500) NOT NU…...
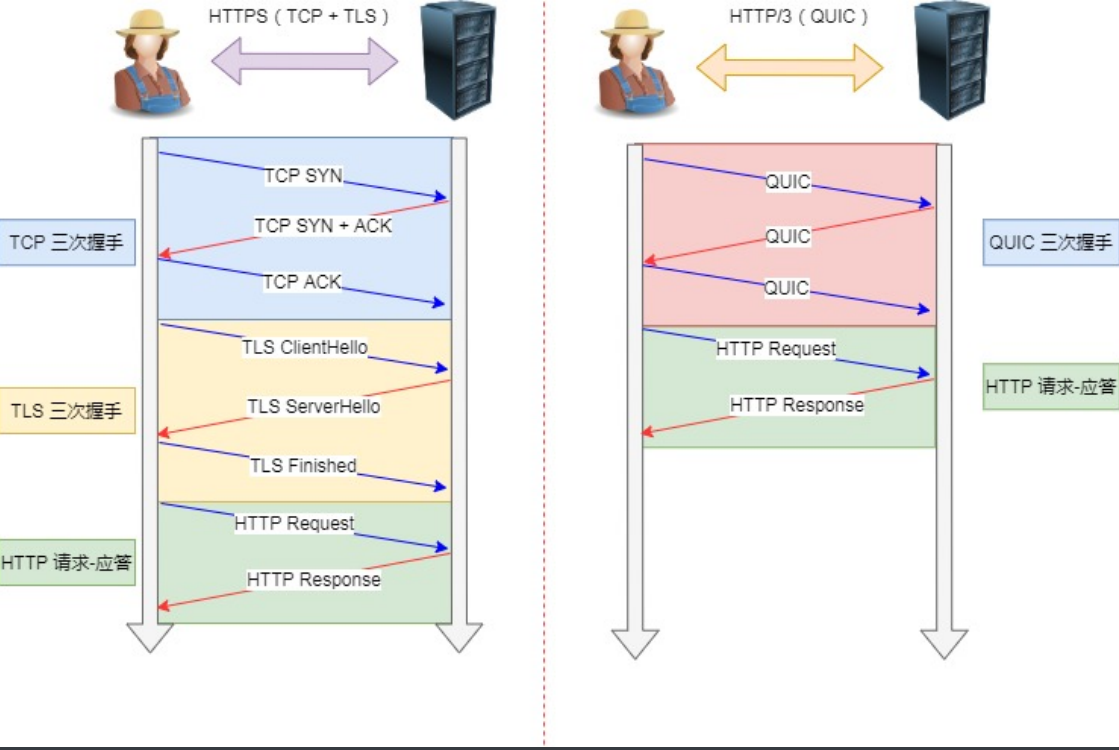
http、https笔记
目录 HTTP 基本概念状态码:get和post的区别:http 常⻅字段:http的缺点: HTTP/1.1HTTP/3HTTPSHTTPS和HTTP区别对称加密和⾮对称加密⾮对称加密 HTTP 基本概念 状态码: 1xx 中间状态,比如post的continue 20…...

飞凌嵌入式「国产」嵌入式核心板大盘点(三)——龙芯中科、赛昉科技
为了帮助各位工程师朋友详细了解飞凌嵌入式推出的“国产化”产品,小编专门开设了「国产平台大盘点专题」。上周,已经带大家盘点了飞凌嵌入式联合瑞芯微电子和全志科技两个国产处理器品牌打造的平台,今天,将继续为大家介绍龙芯和赛…...
)
以vue2为例,用npm开发环境在后端部署vue2项目(更推荐使用nginx部署)
因为之前一致出现的跨域问题,从而想到了这个办法,属于偏方。推荐使用nginx部署,再去解决跨域问题。 接下来聊一聊本文所使用的方法。 首先将你的前端vue项目拷贝一份到服务器,准备一个dockerfile文件,用这个进行部署首…...

docker容器监控:Cadvisor +Prometheus+Grafana的安装部署
目录 Cadvisor PrometheusGrafana的安装部署 一、安装docker: 1、安装docker-ce 2、阿里云镜像加速器 3、下载组件镜像 4、创建自定义网络 二、部署Cadvisor 1、被监控主机上部署Cadvisor容器 2、访问cAdvisor页面 三、安装prometheus 1、部署Prometheus…...
前端食堂技术周刊第 93 期:7 月登陆 Web 平台的新功能、Node.js 工具箱、Nuxt3 开发技巧、MF 重构方案
美味值:🌟🌟🌟🌟🌟 口味:橙橙冰萃美式 食堂技术周刊仓库地址:https://github.com/Geekhyt/weekly 大家好,我是童欧巴。欢迎来到前端食堂技术周刊,我们先来…...
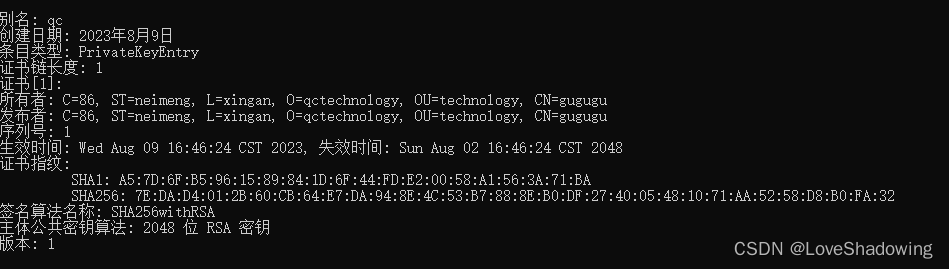
获取 Android 的 SHA1 值
1、调试版,可以直接在 Android studio 中的 gradle 中查看。也可以用下面方法进行 前提要先确定签名文件所在的路径:调试版默认使用的签名文件是debug.keystore,文件处于 C 盘用户目录下的.android文件夹下。打开命令行工具, 1、…...
)
! [remote rejected] develop -> develop (pre-receive hook declined)
问题 git push 远程提交dao develop 分支失败,出现下面错误信息 remote: GitLab: You are not allowed to push code to protected branches on this project. To https://xxx.com.cn/xxx/xxx/xxx/xxx.git/! [remote rejected] develop -> develop (pre-receiv…...
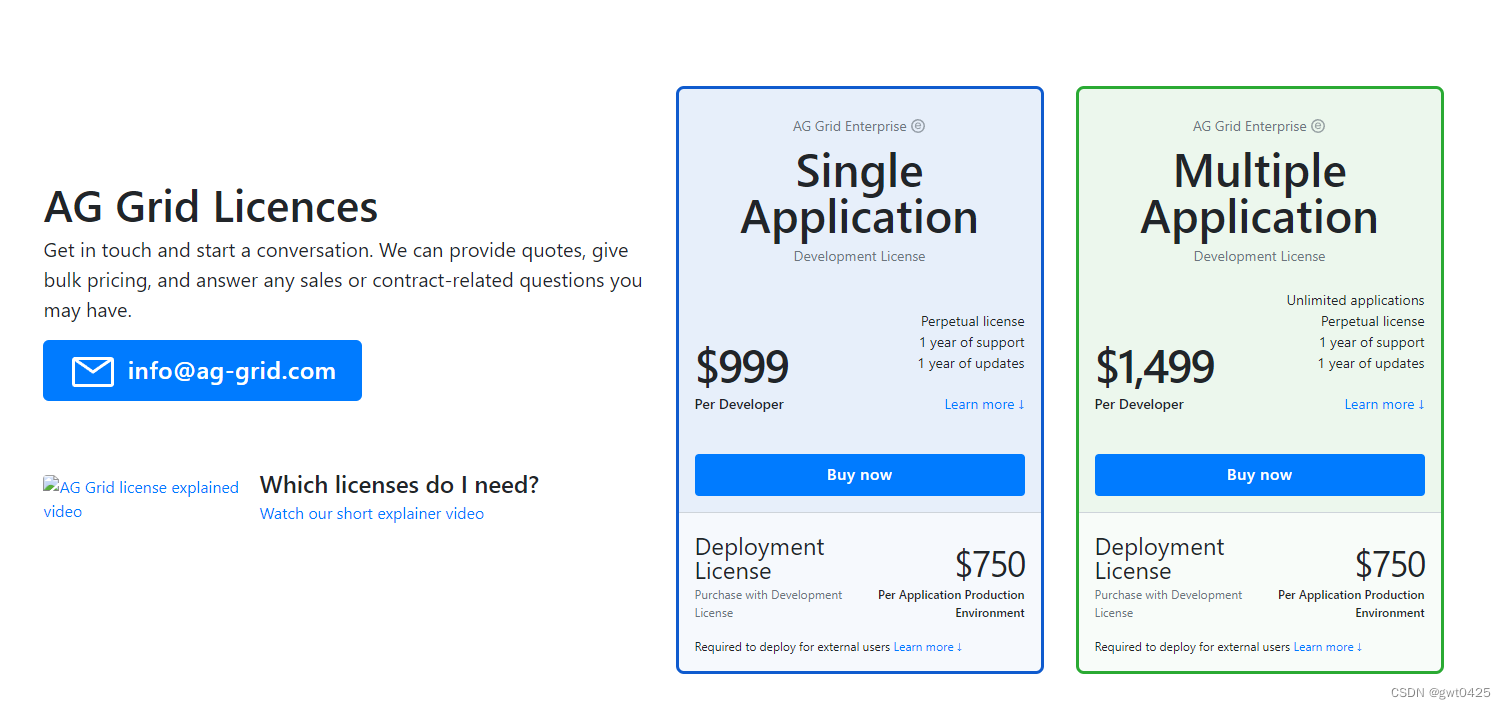
最强的表格组件—AG Grid使用以及License Key Crack
PS: 想要官方 License Key翻到最后面 Ag Grid简介 Ag-Grid 是一个高级数据网格,适用于JavaScript/TypeScript应用程序,可以使用React、Angular和Vue等流行框架进行集成。它是一种功能强大、灵活且具有高度可定制性的表格解决方案,提供了丰富…...
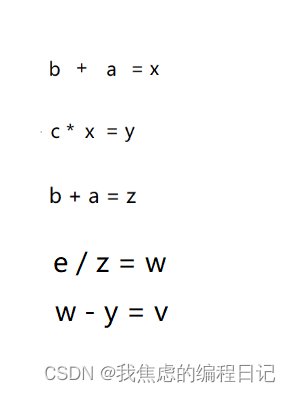
【算法】逆波兰表达式
文章目录 定义求法代码思想: 定义 逆波兰表达式也称为“后缀表达式”,是将运算符写在操作数之后的运算式。 求法 *如:(ab)c-(ab)/e的转换过程: 先加上所有的括号。 (((ab)*c)-((ab)/e))将所有的运算符移到括号外面 (((ab) c)* …...
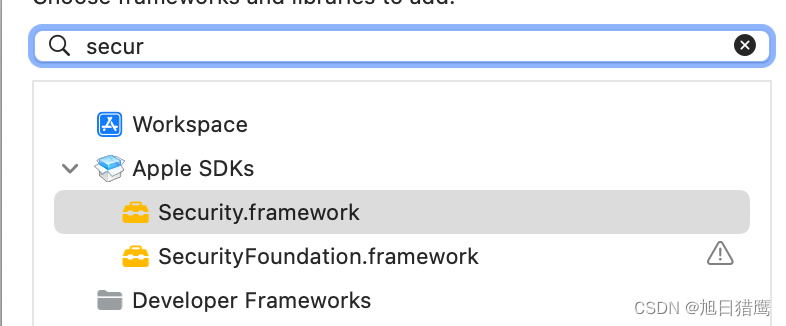
添加SQLCipher 到项目中
文章目录 一、克隆下载SQLCipher二、手动导入1. 生成sqlite3.c2. 在项目中添加命令3. 添加 Security.framework 三、CocoaPods导入 SQLCipher官方地址 一、克隆下载SQLCipher $ cd ~/Documents/code $ git clone https://github.com/sqlcipher/sqlcipher.git二、手动导入 1.…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...

【C++】纯虚函数类外可以写实现吗?
1. 答案 先说答案,可以。 2.代码测试 .h头文件 #include <iostream> #include <string>// 抽象基类 class AbstractBase { public:AbstractBase() default;virtual ~AbstractBase() default; // 默认析构函数public:virtual int PureVirtualFunct…...

redis和redission的区别
Redis 和 Redisson 是两个密切相关但又本质不同的技术,它们扮演着完全不同的角色: Redis: 内存数据库/数据结构存储 本质: 它是一个开源的、高性能的、基于内存的 键值存储数据库。它也可以将数据持久化到磁盘。 核心功能: 提供丰…...

stm32wle5 lpuart DMA数据不接收
配置波特率9600时,需要使用外部低速晶振...
