链表有无环以及确定入环口详解
142.环形链表 II
给定一个链表的头节点 head ,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。如果 pos 是 -1,则在该链表中没有环。注意:pos 不作为参数进行传递,仅仅是为了标识链表的实际情况。
不允许修改 链表。
示例 1:
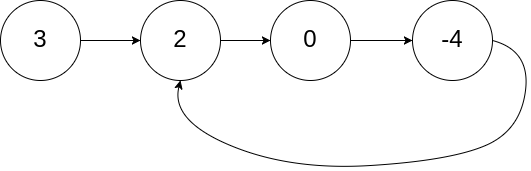
输入:head = [3,2,0,-4], pos = 1
输出:返回索引为 1 的链表节点 解释:链表中有一个环,其尾部连接到第二个节点。
示例 2:
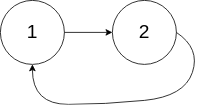
输入:head = [1,2], pos = 0
输出:返回索引为 0 的链表节点 解释:链表中有一个环,其尾部连接到第一个节点。
示例 3:
输入:head = [1], pos = -1
输出:返回 null 解释:链表中没有环。
判断是否有环
算法思想:经典的快慢指针问题,设置快慢指针,slow 和 fast 初始时都指向链表的头结点 head,然后慢指针每次走一步,快指针每次走两步,这样快指针一定比慢指针先入环,经过不断的走下去,若是链表有环,快慢指针必会在环上相遇
#include<iostream>
#include<math.h>
using namespace std;
struct ListNode {int val;ListNode* next;ListNode() : val(0), next(nullptr) {}ListNode(int x) : val(x), next(nullptr) {}ListNode(int x, ListNode* next) : val(x), next(next) {}};bool hasCycle(ListNode* head) {if (head == nullptr || head->next == nullptr) return false; // 链表没有元素或者只有一个元素ListNode* fast = head;ListNode* slow = head;while (fast != nullptr && fast->next != nullptr) {slow = slow->next;fast = fast->next->next;if (slow == fast) return true;}return false;}判断入环口
判断链表的入环口相当于判断两长度不一的链表的公共结点初始位置(长的先走两链表的差值,然后一起走),按道理我们应该让长的链表先走(假设长链表是初始链表,短链表是从环开始的链表),由于链表有环我们无法准确的知道链表的长度,那么如何判断入环口呢?
首先我们应该知道,在 slow 入环的时候,fast 早已入环,那么 slow 和 fast 之间的距离必定小于环长,所以当 fast 和 slow 相遇的时候,slow 在环内走的距离一定小于环长。
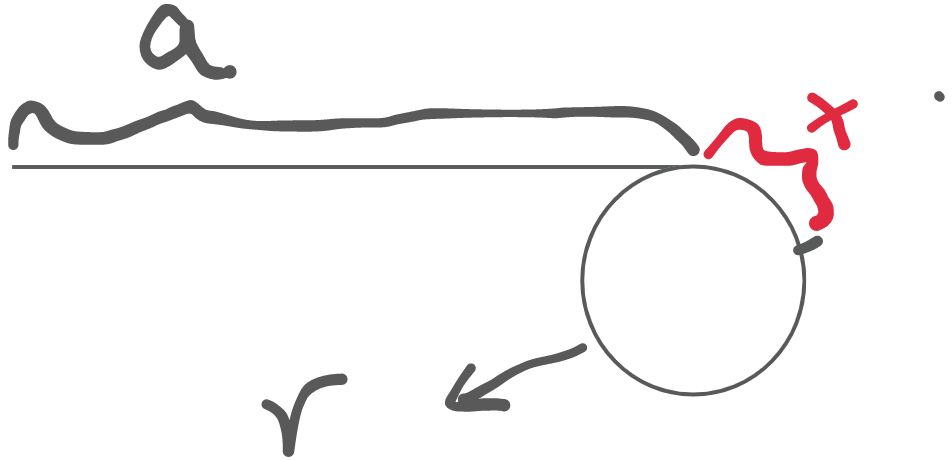
我们假设头结点距离入环口的长度为 a ,fast 和 slow 相遇的位置距离入环口 x ,环的长度为 r .那么由上图可知 slow 走的距离是 a+x,而由于相遇之前 fast 可能已经绕环 n 圈,那么 fast 所走的距离是 a + r*n + x,又由于 fast 所走的步长等于 slow 的两倍,所以 2*(a+x) = a + r*n + x => a = r*n - x。
再回到寻找两链表的公共结点,我们已经知道了链表长度的差值 a,又已知链表是有环的,那么不妨设 h1 = head, h2=slow( 相对于h1已经走了 x ),那么 h1 走完 a 到达入环口的时候,h2 已经绕完环 n 圈也到达了入环口,所以 h1 和 h2 相遇的位置便是入环口的位置。
/*142. 环形链表 II
*/#include<iostream>
using namespace std;/* 链表类型 */
typedef struct ListNode {int val;ListNode* next;ListNode() : val(0), next(nullptr) {}ListNode(int x) : val(x), next(nullptr) {}ListNode(int x, ListNode* next) : val(x), next(next) {}};ListNode* detectCycle(ListNode* head) {if (head == nullptr || head->next == nullptr) return nullptr;if (head->next == head) return head; // 只有头结点ListNode* fast = head;ListNode* slow = head;while (fast != nullptr && fast->next != nullptr) {slow = slow->next;fast = fast->next->next;if (slow == fast) break;}if (fast == nullptr || fast->next == nullptr) return nullptr; // 无环ListNode* h1 = head;ListNode* h2 = slow;while (h1 != h2) {h1 = h1->next;h2 = h2->next;}return h1; // 入环口
}over!
相关文章:

链表有无环以及确定入环口详解
142.环形链表 II 给定一个链表的头节点 head ,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。 如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测…...

chrome插件开发实例08- 使用Vue.js开发chrome插件
目录 背景 演示 功能介绍 插件下载 注意写法: 背景 将 下面的两个插件 改写成vue.js , elementui 实现chrome插件开发实例0...

PCL 计算外接圆的半径
目录 一、算法原理1、计算公式2、主要函数3、源码解析二、代码实现三、结果展示四、参考链接本文由CSDN点云侠原创,原文链接。爬虫自重。 一、算法原理 1、计算公式...
)
Matlab实现神经网络SOM算法(附上完整仿真源码)
神经网络SOM算法是一种基于自组织的无监督学习算法,其全称为Self-Organizing Map,可以用来对数据进行聚类和可视化。本文将介绍如何使用Matlab实现神经网络SOM算法。 文章目录 一、准备工作二、数据准备三、SOM算法实现四、聚类结果分析五、总结六、完整…...
【遍历】非递归法 二叉树的前中后序遍历
文章目录 非递归法前序遍历后序遍历中序遍历 递归法DFS 非递归法 通过栈Stack来模拟递归。 前序遍历 LeetCode 144 前序遍历:1 2 3 定义:存放答案的List、栈Stack 将root入栈出栈:node,为null则舍弃将node放入list将node.r…...

Python将tiff转换成png
文章目录 问题描述解决方案压缩并转换参考文献 问题描述 base64 的 image/tiff 无法在页面直接展示,将其转换为 image/png 解决方案 from io import BytesIOfrom PIL import Imagewith Image.open(a.tiff) as image:bytesIO BytesIO()image.save(bytesIO, format…...

【大数据】-- 部署 Flink kubernetes operator
目录 1.说明 1.1 版本 1.2 kubernetes 环境 1.3 参考 2.安装步骤 2.1 安装本地 kubernetes 环境...
方式)
能够完成两个数的算术运算的单地址指令,地址码指明一个操作数,另一个操作数来自( )方式
【计算机组成原理错题】能够完成两个数的算术运算的单地址指令,地址码指明一个操作数,另一个操作数来自( )方式。 A.立即寻址 B.隐含寻址 C.间接寻址 D.基址寻址 正确答案:B 因为另一个操作数来自于累加器ACC,而这种方式属于隐含寻址。 在指令…...
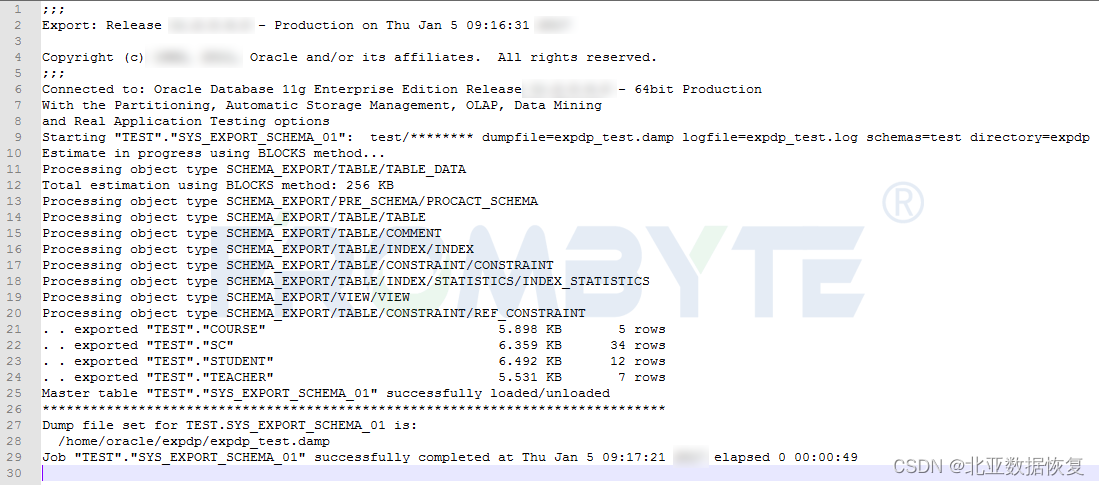
数据库数据恢复-Oracle数据库数据恢复案例
数据库数据恢复环境: Oracle数据库ASM磁盘组有4块成员盘。 数据库故障&分析: Oracle数据库ASM磁盘组掉线 ,ASM实例无法挂载,用户联系我们要求恢复oracle数据库。 数据库数据恢复工程师拿到磁盘后,先将所有磁盘以只…...

对于msvcr120.dll丢失的问题,分享几种解决方法
msvcr120.dll的作用是提供一系列的运行时函数和功能,以便应用程序能够正常运行。这些函数和功能包括内存管理、异常处理、输入输出操作、数学运算等。在没有这个库文件的情况下,应用程序可能无法正常启动或执行特定的功能,甚至会出现错误提示…...
网络安全进阶学习第十三课——SQL注入Bypass姿势
文章目录 一、等号被过滤二、substr、mid等被过滤三、逗号被过滤四、and/or被过滤五、空格被过滤五、其他绕过方式 一、等号被过滤 1、like,rlike语句,其中rlike是正则2、大于号>,小于号<3、符号<>:<>为不等于…...

vue3 provide inject实现强制刷新
1、在 App.vue 文件里写入 provide 的方法 <template> <div id"app"><keep-alive> <router-view v-if"isRouterAlive"></router-view></keep-alive> </div> </template> <script> export default …...
Neo4j笔记-数据迁移(导出/导入)
这里先说明以下几点: Neo4j在4.0下版本默认的库名是:graph.db Neo4j在4.0上版本默认的库名是:neo4j.db 不管是Neo4j,还是Neo4j Desktop,都会在bin目录下有neo4j、neo4j-admin软件。在conf目录下,有neo4j.…...
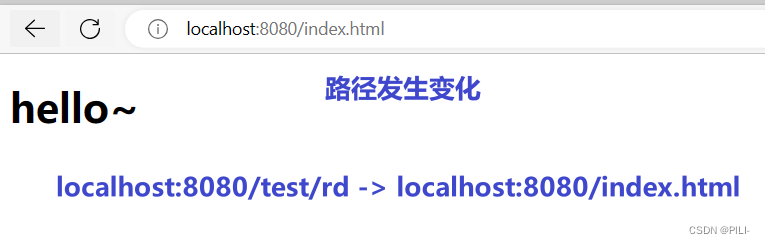
请求转发和请求重定向
目录 1. 定义层面 2. 请求方层面 3. 数据共享层面 4. 最终 url 层面 5. 代码实现层面 请求转发 请求重定向 在Java中,跳转网页的方式有两种,一种是请求转发,另一种是请求重定向,而实际上,这两种方式是有着明显…...
TOMCAT的多实例部署和动静分离
tomcat的多实例 动静分离 排错小工具: telnet工具:yum -y install telnet telnet工具用于测试端口是否正常 telnet 20.0.0.101 80Tomcat多实例部署: 一台服务器上有多个tomcat的服务 1.安装好 jdk 2.安装 tomcat cd /opt tar zxvf apache-…...

阿里微服务seata组件tc告诉rm进行提交的时候,rm提交失败了seata怎么办呢?
当Seata的TC(Transaction Coordinator)向RM(Resource Manager)发起提交请求时,如果RM提交失败,Seata会采取以下步骤处理: 重试机制:Seata会尝试多次向RM发送提交请求,以确…...

已解决 RuntimeError: There is no current event loop in thread ‘Thread-1‘.
作者主页:爱笑的男孩。的博客_CSDN博客-深度学习,活动,python领域博主爱笑的男孩。擅长深度学习,活动,python,等方面的知识,爱笑的男孩。关注算法,python,计算机视觉,图像处理,深度学习,pytorch,神经网络,opencv领域.https://blog.csdn.net/Code_and516?typeblog个…...
Android的学习系列之Android Studio Setup安装
Android的学习系列之Android Studio Setup安装 [TOC](Android的学习系列之Android Studio Setup安装) 前言Android平台搭建总结 前言 还是项目需要,暂时搭建安卓的运行平台。 Android平台搭建 安装包 双击安装包,进入安装。 下一步 根据自己需求&a…...

Python测试框架pytest:常用参数、查找子集、参数化、跳过
Pytest是一个基于python的测试框架,用于编写和执行测试代码。pytest主要用于API测试,可以编写代码来测试API、数据库、UI等。 pytest是一个非常成熟的全功能的Python测试框架,主要有以下几个优点: 简单灵活,容易上手。…...
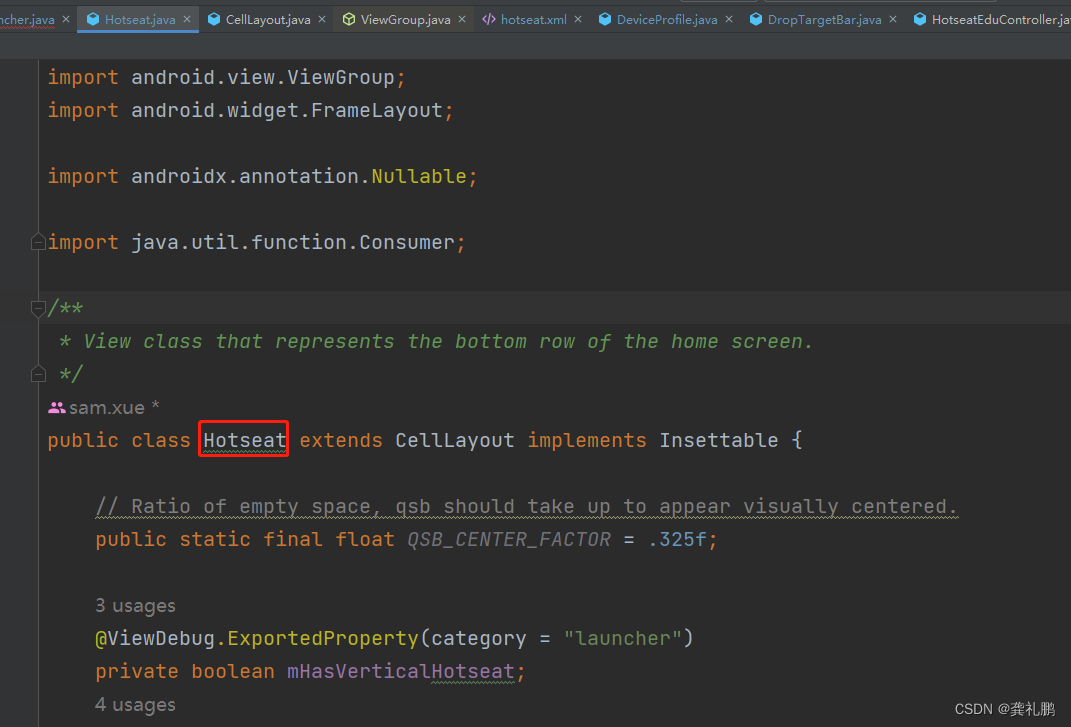
Android 13 Hotseat定制化修改
一.背景 由于需求是需要自定义修改Hotseat,所以此篇文章是记录如何自定义修改hotseat的,应该可以覆盖大部分场景,修改点有修改hotseat布局方向,hotseat图标数量,hotseat图标大小,hotseat布局位置,hotseat图标禁止形成文件夹,hotseat图标禁止移动到Launcher中,下面开始…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...