Java不可变集合详解
什么是不可变集合
不可变集合,英文叫 immutable
顾名思义就是说集合是不可被修改的。集合的数据项是在创建的时候提供,并且在整个生命周期中都不可改变。
为什么要使用不可变集合
不可变对象有很多优点,包括:
- 当对象被不可信的库调用时,不可变形式是安全的
- 不可变对象被多个线程调用时,不存在竞态条件问题
- 不可变集合不需要考虑变化,因此可以节省时间和空间。所有不可变的集合都比它们的可变形式有更好的内存利用率(分析和测试细节)
- 不可变对象因为有固定不变,可以作为常量来安全使用
创建对象的不可变拷贝是一项很好的防御性编程技巧。Guava为所有JDK标准集合类型和Guava新集合类型都提供了简单易用的不可变版本。
Java 9 版本以前, Collections提供了一组方法把可变集合封装成不可变集合,假如要创建一个包含 几个元素的 Set 集合,程序需要先创建 Set 集合,然后调用 几次 add() 方法向 Set 集合中添加元素。例如:
List<String> list = new ArrayList<String>();list.add("a");list.add("b");list.add("c");List<String> unmodifiableList = Collections.unmodifiableList(list);list.add("d");System.out.println(unmodifiableList);输出的结果: [a,b,c,d]
得出结论:Collections.unmodifiableList 实现的不是真正的不可变集合,当原始集合修改后,不可变集合也发生变化。
- 笨重而且累赘:不能舒适地用在所有想做防御性拷贝的场景;
- 不安全:要保证没人通过原集合的引用进行修改,返回的集合才是事实上不可变的;
- 低效:包装过的集合仍然保有可变集合的开销,比如并发修改的检查、散列表的额外空间,等等。
如果你没有修改某个集合的需求,或者希望某个集合保持不变时,把它防御性地拷贝到不可变集合是个很好的实践。
但是Java 9 出了些新的生成不可变集合的方法,程序直接调用 Set、List、Map 的 of() 方法即可创建包含 N 个元素的不可变集合,这样一行代码就可创建包含 N 个元素的集合。
不可变意味着程序不能向集合中添加元素,也不能从集合中删除元素。
如下程序示范了如何创建不可变集合。
public class Java9Collection {
public static void main(String[] args) {
// 创建包含4个元素的Set集合
Set set = Set.of("Java", "Kotlin", "Go", "Swift");
System.out.println(set);
// 不可变集合,下面代码导致运行时错误
// set.add("Ruby");
// 创建包含4个元素的List集合List list = List.of(34, -25, 67, 231);
System.out.println(list);
// 不可变集合,下面代码导致运行时错误
// list.remove(1);
// 创建包含3个key-value对的Map集合Map map = Map.of("语文", 89, "数学", 82, "英语", 92);
System.out.println(map);
// 不可变集合,下面代码导致运行时错误
// map.remove("语文");
// 使用Map.entry()方法显式构建key-value对Map map2 = Map.ofEntries(Map.entry("语文", 89), Map.entry("数学", 82), Map.entry("英语", 92));
System.out.println(map2);}
}从上面代码可以看出 Set、List 比较简单,程序只要为它们的 of() 方法传入 N 个集合元素即可创建 Set、List 集合。
创建不可变的 Map 集合有两个方法。使用 of() 方法时只要依次传入多个 key-value 对即可;还可使用 ofEntries() 方法,该方法可接受多个 Entry 对象,因此程序显式使用 Map.entry() 方法来创建 Map.Entry 对象。
相关文章:

Java不可变集合详解
什么是不可变集合 不可变集合,英文叫 immutable 顾名思义就是说集合是不可被修改的。集合的数据项是在创建的时候提供,并且在整个生命周期中都不可改变。 为什么要使用不可变集合 不可变对象有很多优点,包括: 当对象被不可信的…...

常见的JavaScript日常问题
在众多的编程语言中, JavaScript 给大部分的人的第一印象是人畜无害,看起来就简单的,对稍微有点儿开发经验的人来说,在网页中写个JavaScript功能也相当简单。但是当你真的得了解了JavaScript之后就会发现,它比我们想象…...

css modules的用法和在react项目中的应用
参考文章 CSS Modules 的用法 CSS Modules 的功能很单纯,只加入了局部作用域和模块依赖,可以保证某个组件的样式,不会影响到其他组件。 局部作用域 CSS的规则都是全局的,任何一个组件的样式规则,都对整个页面有效。…...
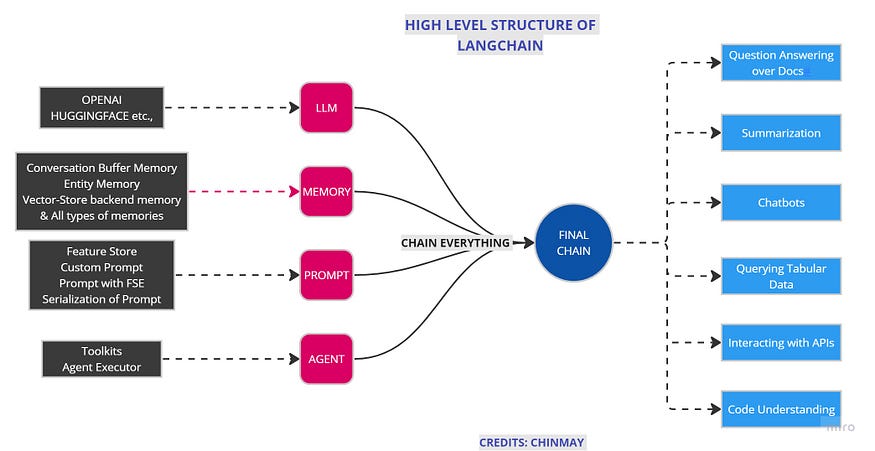
【LangChain概念】了解语言链️:第2部分
一、说明 在LangChain的帮助下创建LLM应用程序可以帮助我们轻松地链接所有内容。LangChain 是一个创新的框架,它正在彻底改变我们开发由语言模型驱动的应用程序的方式。通过结合先进的原则,LangChain正在重新定义通过传统API可以实现的极限。 在上一篇博…...

步入React前厅 - Css In React
目录 扩展学习资料 行内样式 引入样式表 CSS Module /src/components/common.module.css /src/components/listitem.module.css css管理进阶 Css管理工具 练习 扩展学习资料 资料名称 链接 css module CSS Modules 用法教程 - 阮一峰的网络日志 在React中使…...
——图像分割(二))
OpenCV(三)——图像分割(二)
目录 4.边缘检测 4.1 图像梯度的概念 4.2 模板卷积和梯度图的概念 4.3 梯度算子...
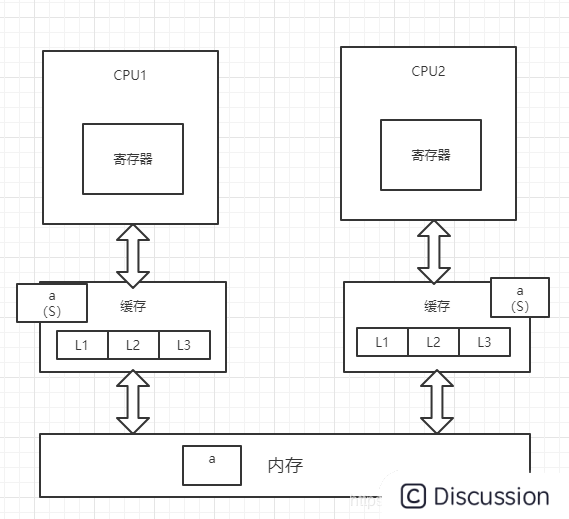
28.Netty源码之缓存一致性协议
Mpsc Queue 基础知识 Mpsc 的全称是 Multi Producer Single Consumer,多生产者单消费者。Mpsc Queue 可以保证多个生产者同时访问队列是线程安全的,而且同一时刻只允许一个消费者从队列中读取数据。 Netty Reactor 线程中任务队列 taskQueue 必须满足多个…...

造个轮子-任务调度执行小框架-任务清单执行恢复实现
文章目录 前言恢复执行流程失败任务执行重启执行中任务恢复执行修复组件整合组件整合容器启动类总结前言 okey,通过前面的两篇文章,关于这个任务执行这一块,我想应该是明白了。但是这里的话,还是不够的。我们希望对于任务还可以做到执行失败的重试执行,关于这个意外宕机的…...

若依部署前后端
打包项目 前端打包 npm run build:prod将代码上传到指定目录 配置nginx转发 server{listen 8090;server_name localhost;location / {root /home/cc_library/dist;index index.html index.htm;# 配置 history模式,刷新页面会404,,因为服…...

2009年上半年 软件设计师 下午试卷
博主介绍:✌全网粉丝3W,全栈开发工程师,从事多年软件开发,在大厂呆过。持有软件中级、六级等证书。可提供微服务项目搭建与毕业项目实战,博主也曾写过优秀论文,查重率极低,在这方面有丰富的经验…...

SpringBoot使用自定义事件监听器的demo
记录一下SpringBoot自定义事件监听器的使用方法 案例源码:SpringBoot使用自定义事件监听器的demo 使用的SpringBoot2.0.x版本 <parent><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-parent</artifactId><…...

arcgis定义投影与投影
1、定义 地理坐标系(GCS):利用地球表面的经纬度表示的坐标系统。一般单位为度。投影坐标系(PCS):利用数学换算将三维地球表面上的经纬度坐标转换到二维平面上的坐标系统。一般单位为米。可以认为ÿ…...
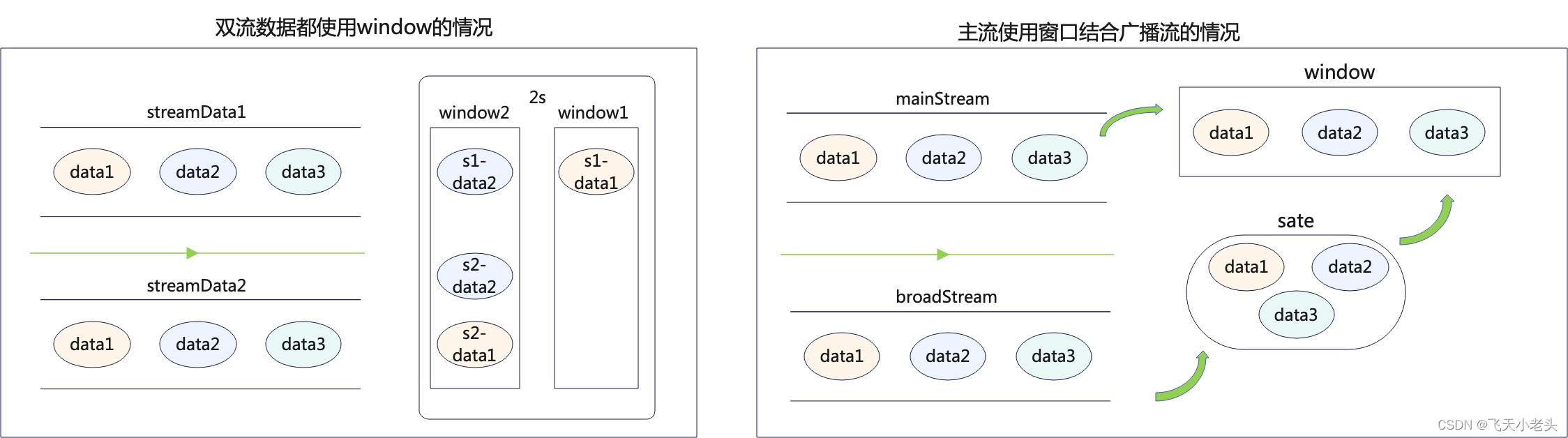
Flink多流处理之Broadcast(广播变量)
写过Spark批处理的应该都知道,有一个广播变量broadcast这样的一个算子,可以优化我们计算的过程,有效的提高效率;同样在Flink中也有broadcast,简单来说和Spark中的类似,但是有所区别,首先Spark中的broadcast是静态的数据,而Flink中的broadcast是动态的,也就是源源不断的数据流.在…...
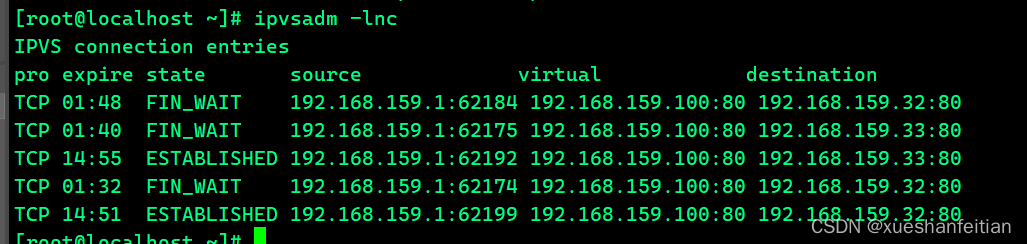
LVS/DR+Keepalived负载均衡实战(一)
引言 负载均衡这个概念对于一个IT老鸟来说再也熟悉不过了,当听到此概念的第一反应是想到举世闻名的nginx,但殊不知还有一个大名鼎鼎的负载均衡方案可能被忽略了,因为对于一般系统来说,很多应用场合中采用nginx基本已经满足需求&a…...

测试DWPose的onnx +Unity barracuda
环境: Unity Barracuda 3.0.1 从github直接拉取的barracuda仓库才能装到这个版本Barracuda以后不再升级了,会迁移到Unity AI大计划里的Sentis 我想申请的来着但好像已经不开放了 Unity 2021.3.20模型:dw-ll_ucoco_384.onnx 报了一些错&…...
轻装上阵,不调用jar包,用C#写SM4加密算法【卸载IKVM 】
前言 记得之前写了一个文章,是关于java和c#加密不一致导致需要使用ikvm的方式来进行数据加密,主要是ikvm把打包后的jar包打成dll包,然后Nuget引入ikvm,从而实现算法的统一,这几天闲来无事,网上找了一下加密…...
redis学习笔记(一)
文章目录 一、引言二、redis介绍2.1、定义2.2、Redis的数据类型及主要特性2.3、Redis的应用场景有哪些? 三、redis环境安装3.1、下载和安装 一、引言 在Web应用发展的初期,那时关系型数据库受到了较为广泛的关注和应用,原因是因为那时候Web站…...

最优化问题 - 拉格朗日对偶
primal 原问题 dual 对偶问题 目标函数 约束条件 可行域D 对偶专题 “拉格朗日对偶问题”如何直观理解?“KKT条件” “Slater条件” “凸优化”打包理解——bilibili 王木头 拉格朗日乘子法与对偶问题...
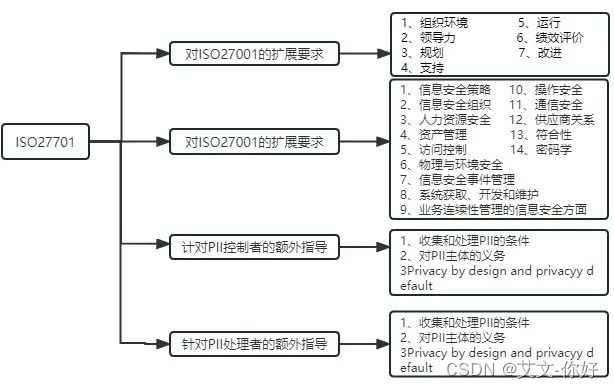
关于ISO27701隐私信息安全管理体系介绍
01 什么是ISO27701 ISO27701是对ISO27001信息安全管理和ISO27002安全控制的隐私扩展,全称《安全技术—扩展ISO27001和ISO27002的隐私信息管理—要求与指南》,是ISO标准委员会以ISO 27001为基准,以ISO27552为蓝本,建立发布的隐私…...
C语言案例 分数列求和-11
题目:有一分数列:2 / 1,3 / 2,5 / 3,8 / 5,13 / 8,21 / 13 …求出这个数列的前20项之和。 程序分析 这是一个典型的分数列数学逻辑题,考究这类题目是需要从已知的条件中找到它们的分布规律 我们把前6荐的分子与分母分别排列出来,…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...

十九、【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建
【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建 前言准备工作第一部分:回顾 Django 内置的 `User` 模型第二部分:设计并创建 `Role` 和 `UserProfile` 模型第三部分:创建 Serializers第四部分:创建 ViewSets第五部分:注册 API 路由第六部分:后端初步测…...

ubuntu22.04 安装docker 和docker-compose
首先你要确保没有docker环境或者使用命令删掉docker sudo apt-get remove docker docker-engine docker.io containerd runc安装docker 更新软件环境 sudo apt update sudo apt upgrade下载docker依赖和GPG 密钥 # 依赖 apt-get install ca-certificates curl gnupg lsb-rel…...

【Java多线程从青铜到王者】单例设计模式(八)
wait和sleep的区别 我们的wait也是提供了一个还有超时时间的版本,sleep也是可以指定时间的,也就是说时间一到就会解除阻塞,继续执行 wait和sleep都能被提前唤醒(虽然时间还没有到也可以提前唤醒),wait能被notify提前唤醒…...
