当前位置： 首页 > news >正文

（统计学习方法|李航）第四章 朴素贝叶斯算法——贝叶斯估计

news 2026/2/11 3:44:08

贝叶斯估计方法：

0c7da5d77c7e4dfe9369f75523df3de4.png1eae0f675c9f4d54abee7605ee7742dd.png
计算男女时只有两个值，所以K=2

贝叶斯估计就是拉普拉斯平滑

 a24583a1f36e4449b4f9d13101c69b8d.png

 估计方法：为什么叫做贝叶斯估计呢？

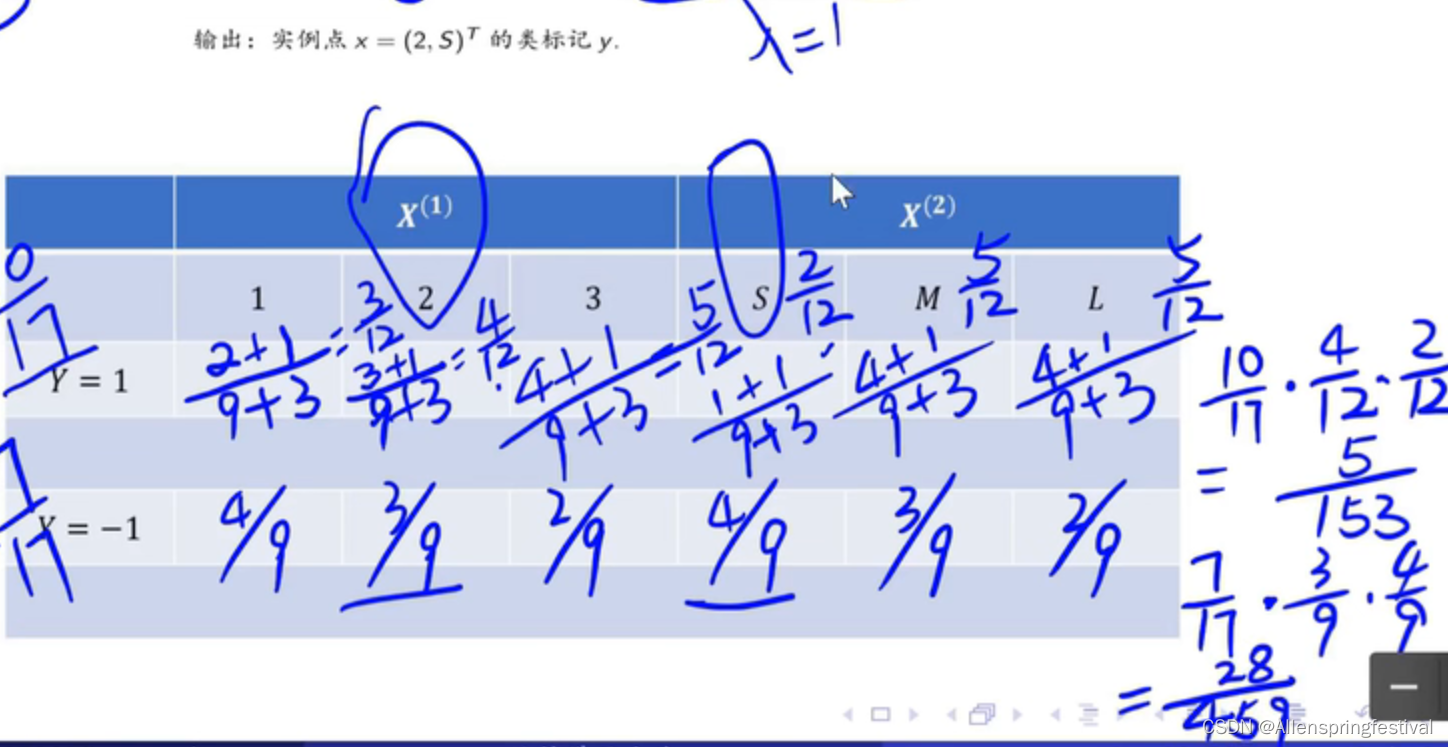
例题：

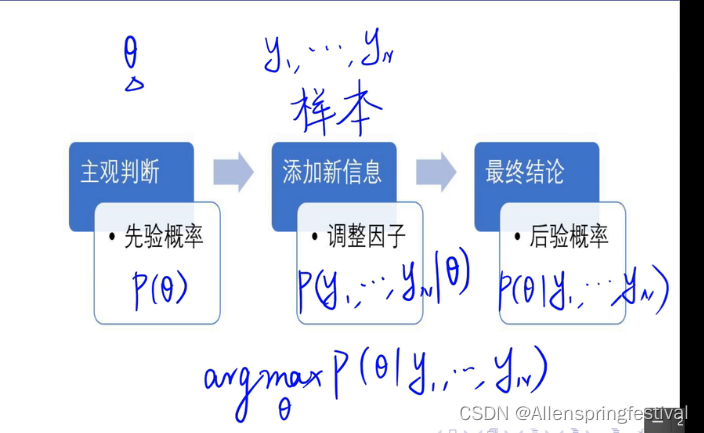
 c52908a58809440083dda5b380303a77.png

 

重新回顾以下朴素贝叶斯：

 f83bc010b34749fe9aa0f2c3bf5489d4.png

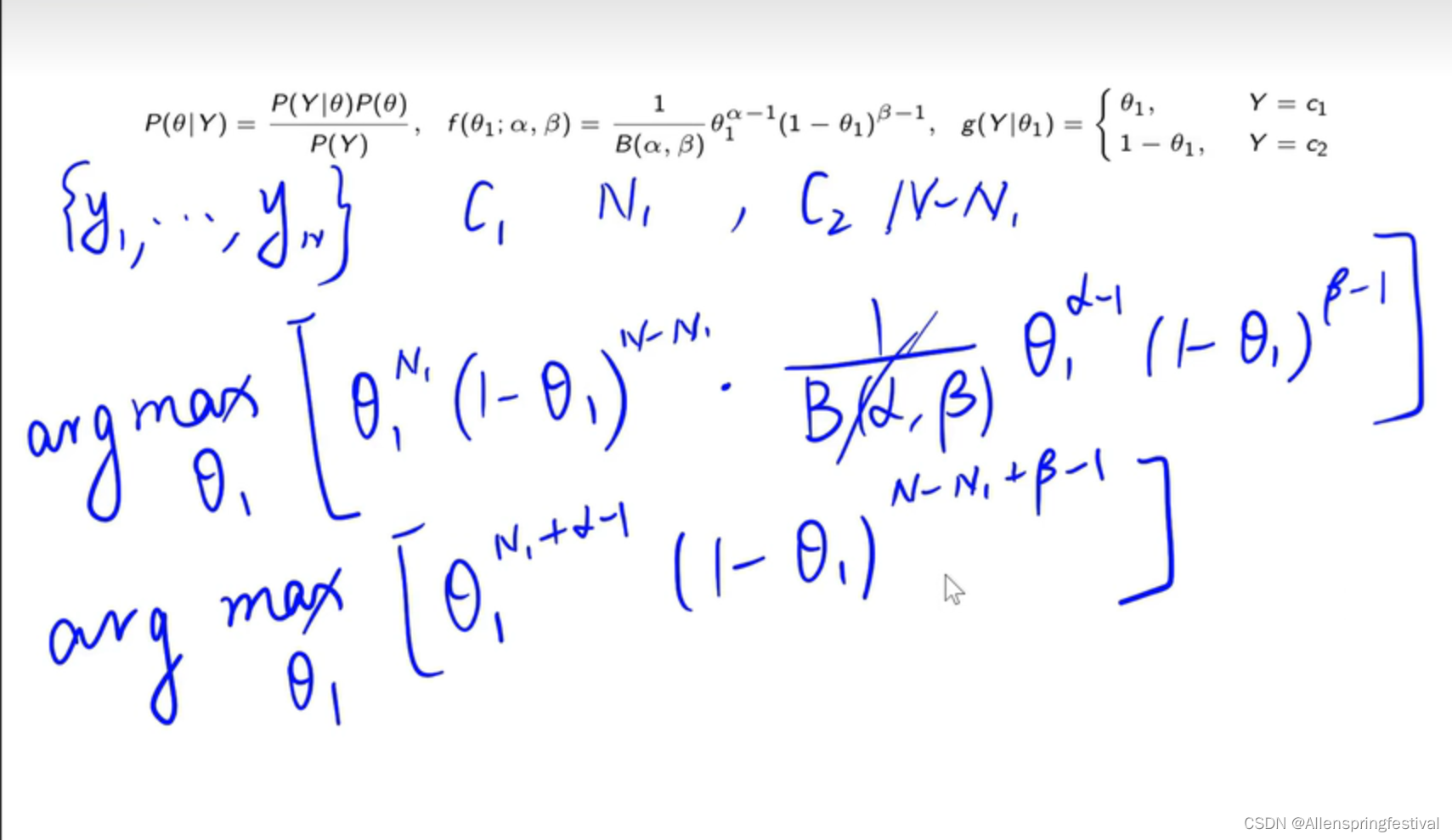
 6a63be4df21840a3a97911ad787aa78b.png

 对他求导，求出最大值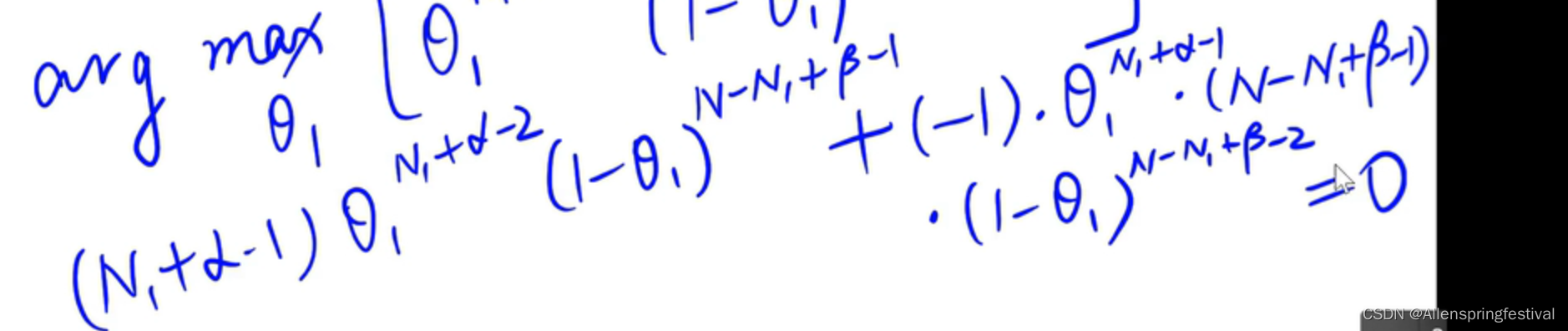b9bb554b00b8411e95ebd7cca3f4bc4e.png

 8f160b26732c493ca1794a1a93fd9af9.png

 得到了色i他的估计值：

e702a5b06a914424b2c37d33bb31d3fc.png

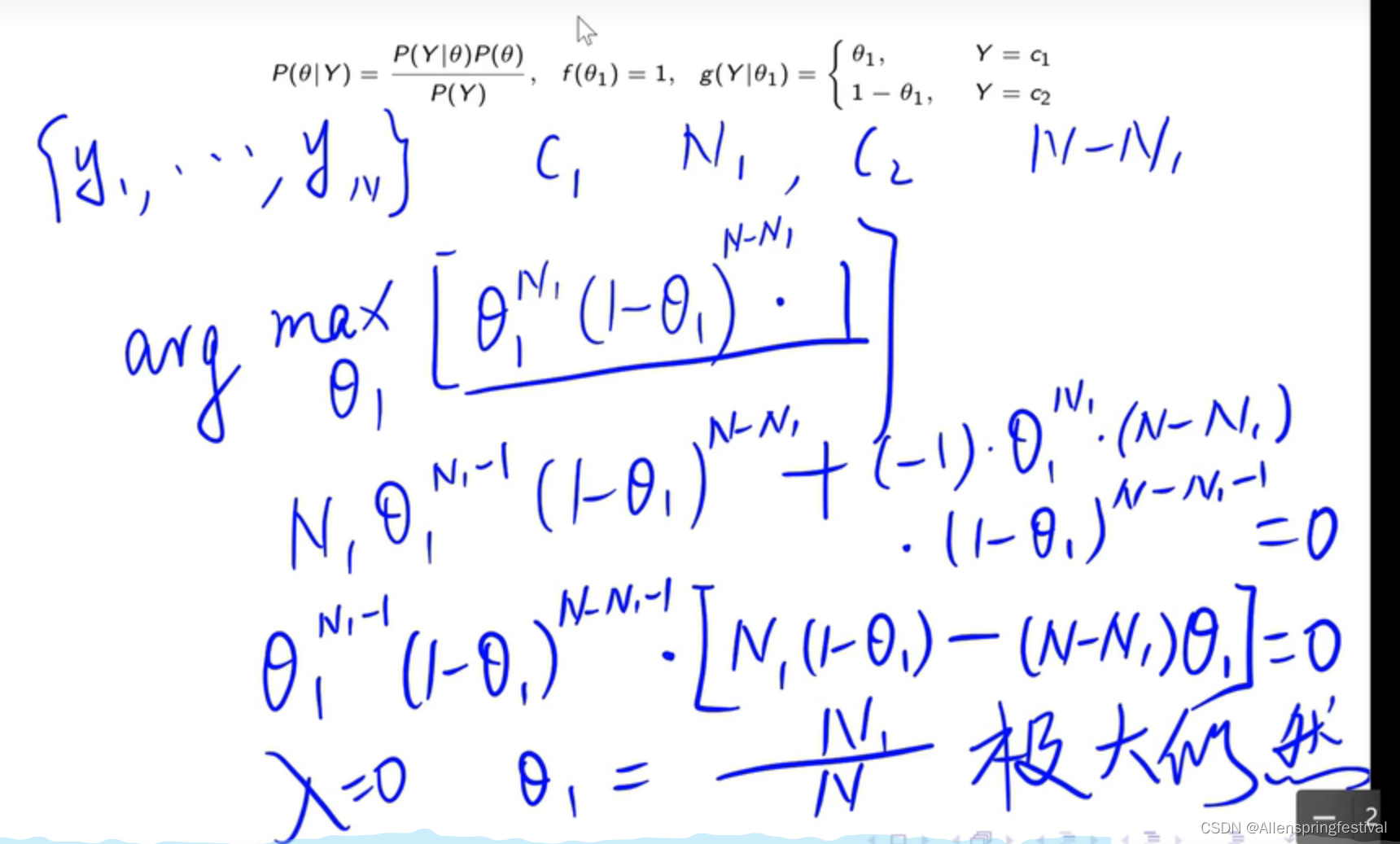
 68dcc9ae76e64947ba96e266730f9b86.png

 0c3edd57520d49edab2ee64a64bf7475.png

 

8e3216b933e04cf7923043cbd0178a10.png

 7116fe4a7ca645a5b813966c4b008078.png

 那么我们可以知道对应Y=-1这类

ebf1379fad914a95bc22c975a710aacd.png

 32721c188b1b431b88309b2165301abf.png

 3b665311f58f4e23afd6434721936a79.png

 006613b8c1f145e78f403733439894b0.png

 女儿国还是特例给自己留点男人

 

相关文章：

（统计学习方法|李航）第四章 朴素贝叶斯算法——贝叶斯估计

贝叶斯估计方法： 计算男女时只有两个值，所以K2 贝叶斯估计就是拉普拉斯平滑 估计方法：为什么叫做贝叶斯估计呢？ 例题： 重新回顾以下朴素贝叶斯： 对他求导，求出最大值 得到了色i他的估计值&…...

编程日记 2023/8/12 10:49:10

企业直播MR虚拟直播（MR混合现实直播技术）视频介绍

到底什么是企业直播MR虚拟直播（MR混合现实直播技术）？ 企业直播MR虚拟直播新玩法（MR混合现实直播技术） 我的文章推荐： [视频图文] 线上研讨会是什么，企业对内对外培训可以用线上研讨会吗&#x…...

编程日记 2023/8/12 10:48:08

React Fiber: 从 Reconciliation 到 Concurrent Mode

React Fiber 是 React 中的一种新的协调算法，它的主要目的是提高 React 的性能和可维护性。在 React Fiber 之前，React 使用了一种叫做 Stack Reconciliation 的算法来处理组件的更新和渲染。但是 Stack Reconciliation 存在一些问题，比如无法…...

编程日记 2023/8/12 10:47:08

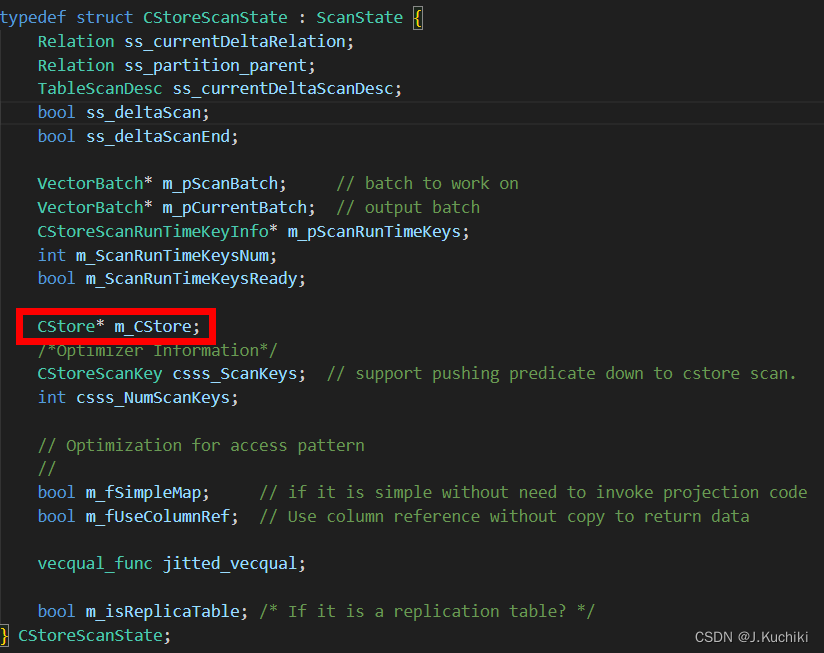
【PostgreSQL内核学习（十一）—— OpenGauss源码学习（CopyTo）】

可优化语句执行 概述什么是列存储？列存的优势 相关函数CopyToCStoreCopyToCopyStatetupleDescCStoreScanDesc CStoreBeginScanRelationSnapshotProjectionInfo GetCStoreNextBatchRunScanFillVecBatchCStoreIsEndScan CStoreEndScan 声明：本文的部分内容…...

编程日记 2023/8/12 10:46:07

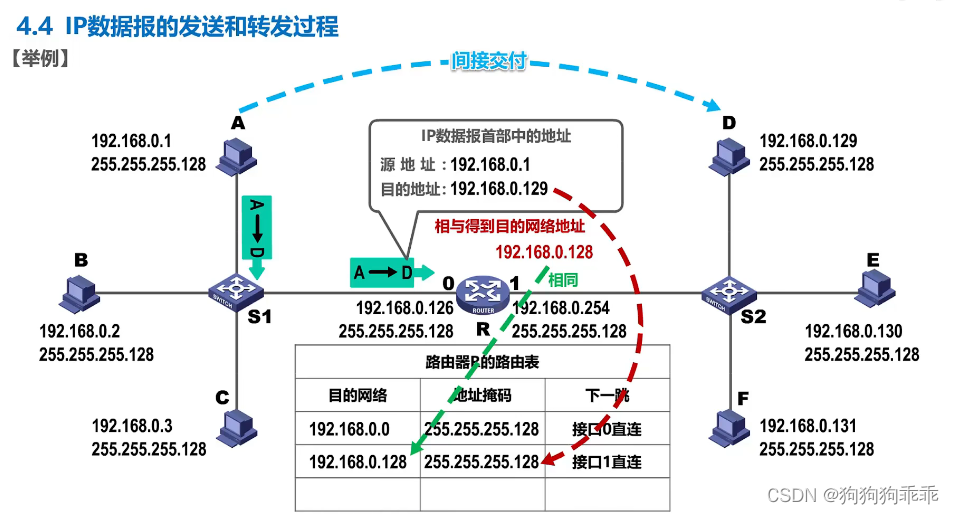
计算机网络 网络层 IPv4地址

A类地址第一位固定0 B类10 其下同理...

编程日记 2023/8/12 10:45:05

【程序员社交】多和高层次人群交流

定义问题：如何多和高层次人群交流获取经验提升自己？ 收集信息：通过社交媒体、行业论坛、行业大会等途径获取高层次人群的信息和观点，并了解他们的工作经历、技能和能力。 分析信息：分析收集到的信息，了解…...

编程日记 2023/8/12 10:44:04

机器学习笔记 - 基于C++的​​深度学习 三、实现成本函数

机器学习中的建模 作为人工智能工程师，我们通常将每个任务或问题定义为一个函数。 例如，如果我们正在开发面部识别系统，我们的第一步是将问题定义为将输入图像映射到标识符的函数F(X)。但是问题是如何知道F(X)公式？ 事实上，使用公式或一系列固有规则来定义F(X)是不可行的（…...

编程日记 2023/8/12 10:43:03

lazada、shopee店铺如何利用测评提高权重和排名？

在 lazada、shopee平台上开店后，卖家们必须对店铺的权重进行更多的关注。如果店铺的权重越高，那么它就会带来更多的流量和更多的订单，那么在 lazada、shopee平台上开设一家店铺，该怎样增加它的店铺权重和排名呢？ laza…...

编程日记 2023/8/12 10:42:01

安全第二次

一&#xff0c;iframe <iframe>标签用于在网页里面嵌入其他网页。 1&#xff0c;sandbox属性 如果嵌入的网页是其他网站的页面&#xff0c;因不了解对方会执行什么操作&#xff0c;因此就存在安全风险。为了限制<iframe>的风险&#xff0c;HTML 提供了sandb…...

编程日记 2023/8/12 10:40:59

125、SpringBoot可以同时处理多少请求？

SpringBoot可以同时处理多少请求？ 一、前言二、线程池4大参数图解三、代码示例一、前言 我们都知道，SpringBoot默认的内嵌容器是Tomcat，也就是我们的程序实际上是运行在Tomcat里的。所以与其说SpringBoot可以处理多少请求，到不如说Tomcat可以处理多少请求。 关于Tomcat的默…...

编程日记 2023/8/12 10:39:58

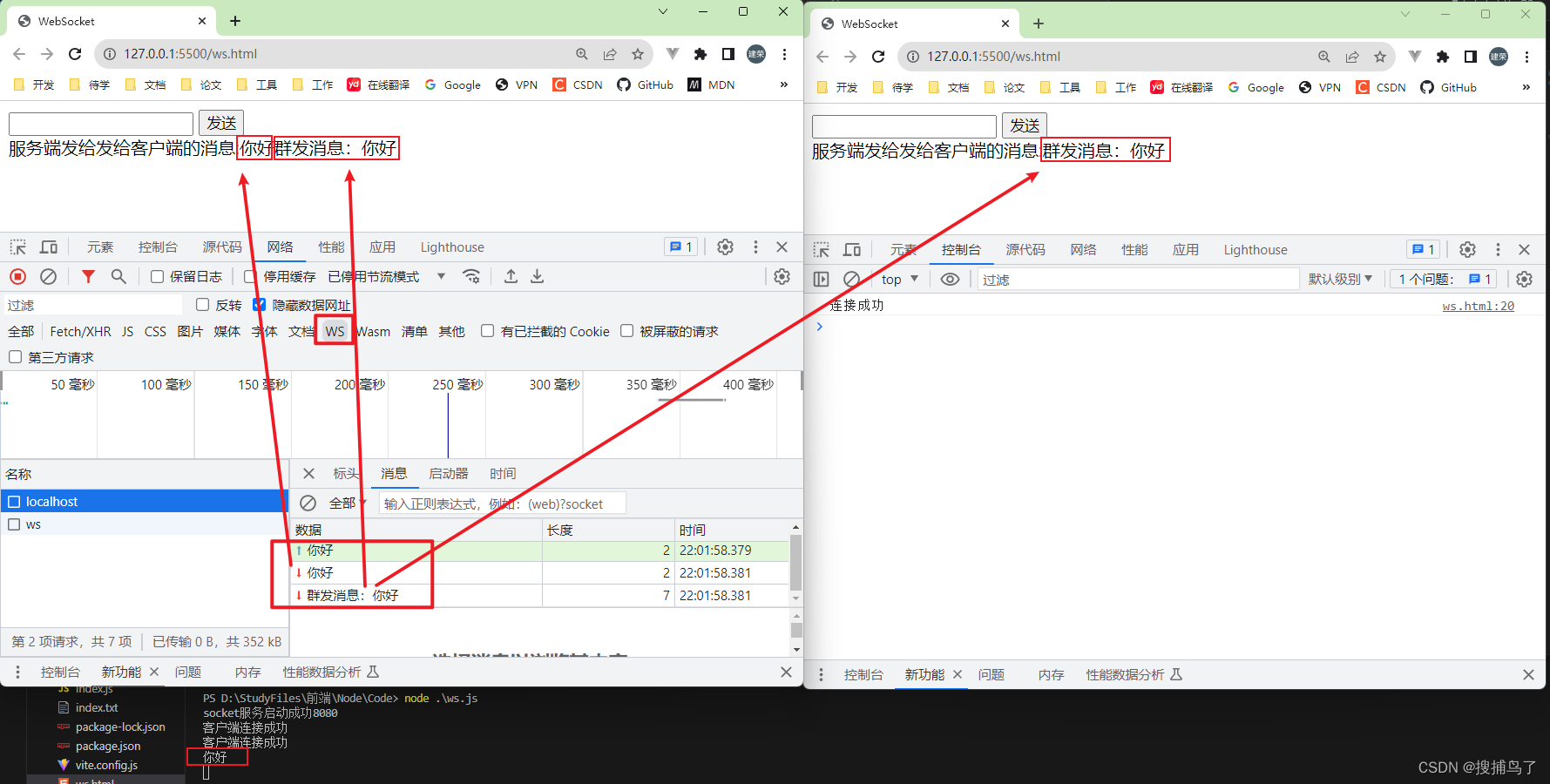
SSE技术和WebSocket技术实现即时通讯

文章目录 一、SSE1.1 什么是SSE1.2 工作原理1.3 特点和适用场景1.4 API用法1.5 代码实现 二、WebSocket2.1 什么是WebSocket2.2 工作原理2.3 特点和适用场景2.4 API用法2.5 代码实现2.6 心跳检测 三、SSE与WebSocket的比较 当涉及到实现实时通信的Web应用程序时&#xff0c;两种…...

编程日记 2023/8/12 10:38:56

什么是敏捷开发？

敏捷开发流程&#xff1a;制度化、规范化地PUA程序员的顶级神器&#xff01;&#xff01;&#xff01;...

编程日记 2023/8/12 10:37:54

tcp发送整型，结构体等数据的方法

测试环境 Receiver: x86 UbuntuSender: arm64 android 发送整型数 C语言和套接字库来发送一个整型变量&#xff08;int&#xff09;的客户端程序。 它首先创建一个TCP套接字&#xff0c;然后连接到指定的服务器地址和端口。接着&#xff0c;它将一个整型变量&#xff08;in…...

编程日记 2023/8/12 10:36:54

【Unity每日一记】让一个物体按余弦曲线移动—（三角函数的简单运用）

&#x1f468;‍&#x1f4bb;个人主页&#xff1a;元宇宙-秩沅 &#x1f468;‍&#x1f4bb; hallo 欢迎 点赞&#x1f44d; 收藏⭐ 留言&#x1f4dd; 加关注✅! &#x1f468;‍&#x1f4bb; 本文由 秩沅 原创 &#x1f468;‍&#x1f4bb; 收录于专栏&#xff1a;uni…...

编程日记 2023/8/12 10:35:52

python爬虫实战——数据可视化

本篇文章将介绍如何利用Python爬虫获取数据并进行可视化展示&#xff0c;包括以下主要内容&#xff1a; 数据获取&#xff1a;使用requests库发送HTTP请求获取目标网页的数据&#xff1b;数据解析&#xff1a;使用BeautifulSoup库对HTML代码进行解析提取所需数据&#xff1b;数…...

编程日记 2023/8/12 10:34:51

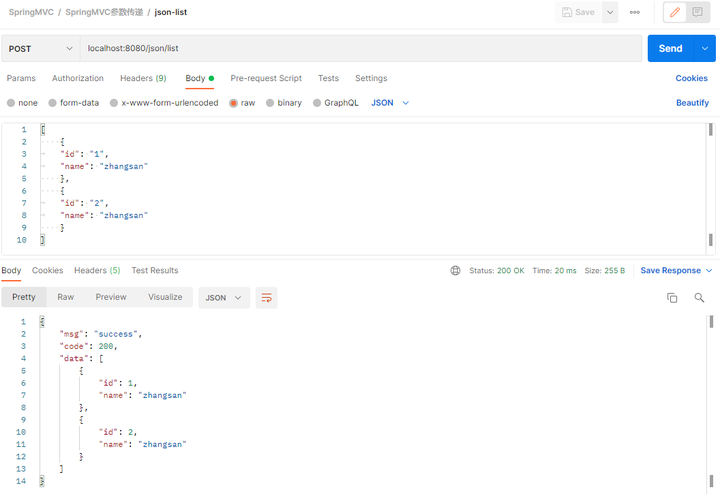
案例13 Spring MVC参数传递案例

基于Spring MVC实现HttpServletRequest、基本数据类型、Java Bean、数组、List、Map、JSON方式的参数传递。 1. 创建项目 选择Maven快速构建web项目&#xff0c;项目名称为case13-springmvc02。 2. 配置Maven依赖 <?xml version"1.0" encoding"UTF-8&quo…...

编程日记 2023/8/12 10:33:50

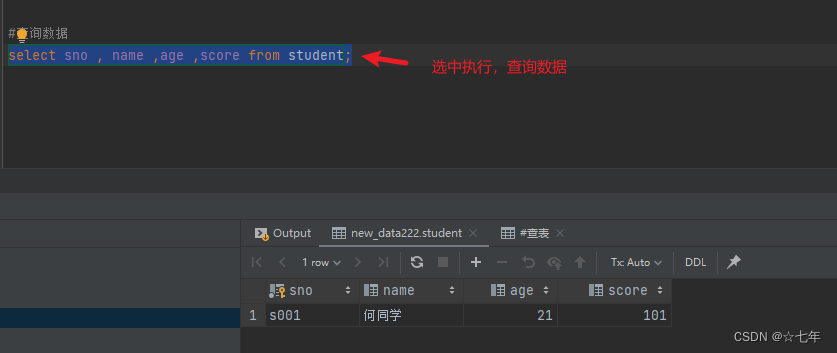
IntellIJ Idea 连接数据库-MySql

前言&#xff1a;可以用mariaDB工具&#xff0c;在本地创建服务器主机和数据库&#xff0c;而后用intellIJ Idea尝试连接 MariaDB创建数据库练习 1.IntellIJ Idea打开界面右侧Database工具&#xff0c;选择MySQL数据库。 2.填写数据库账号密码&#xff0c;地址端口号&#xff…...

编程日记 2023/8/12 10:32:49

通讯协议036——全网独有的OPC HDA知识一之聚合（五）计数

本文简单介绍OPC HDA规范的基本概念&#xff0c;更多通信资源请登录网信智汇(wangxinzhihui.com)。 本节旨在详细说明HDA聚合的要求和性能。其目的是使HDA聚合标准化&#xff0c;以便HDA客户端能够可靠地预测聚合计算的结果并理解其含义。如果用户需要聚合中的自定义功能&…...

编程日记 2023/8/12 10:31:47

【TensorFlow】P0 Windows GPU 安装 TensorFlow、CUDA Toolkit、cuDNN

Windows 安装 TensorFlow、CUDA Toolkit、cuDNN 整体流程概述TensorFlow 与 CUDA ToolkitTensorFlow 是一个基于数据流图的深度学习框架CUDA 充分利用 NIVIDIA GPU 的计算能力CUDA Toolkit cuDNN 安装详细流程整理流程一&#xff1a;安装 CUDA Toolkit步骤一&#xff1a;获取CU…...

编程日记 2023/8/12 10:30:46

基于身份的安全威胁正在迅速增长

根据端点安全和威胁情报供应商 CrowdStrike 发布的一份报告&#xff0c;目前最危险的网络安全威胁是能够访问给定系统合法身份信息的攻击者。 根据该报告&#xff0c;交互式入侵&#xff08;该公司将其定义为攻击者积极工作以在受害者系统上实现某种非法目的的入侵&#xff09;…...

编程日记 2023/8/12 10:29:45

基于ASP.NET+ SQL Server实现（Web）医院信息管理系统

医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上&#xff0c;开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识&#xff0c;在 vs 2017 平台上&#xff0c;进行 ASP.NET 应用程序和简易网站的开发&#xff1b;初步熟悉开发一…...

编程新知 2026/2/10 13:19:02

vscode（仍待补充）

写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh&#xff1f; debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

编程新知 2026/1/24 13:04:10

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别

UnsatisfiedLinkError 在对接硬件设备中&#xff0c;我们会遇到使用 java 调用 dll文件 的情况&#xff0c;此时大概率出现UnsatisfiedLinkError链接错误&#xff0c;原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用&#xff0c;结果 dll 未实现 JNI 协…...

编程新知 2025/10/6 16:38:04

新能源汽车智慧充电桩管理方案：新能源充电桩散热问题及消防安全监管方案

随着新能源汽车的快速普及&#xff0c;充电桩作为核心配套设施&#xff0c;其安全性与可靠性备受关注。然而&#xff0c;在高温、高负荷运行环境下&#xff0c;充电桩的散热问题与消防安全隐患日益凸显&#xff0c;成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

编程新知 2026/1/29 3:00:56

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分

一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计&#xff0c;提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合&#xff1a;各模块职责清晰&#xff0c;便于独立开发…...

编程新知 2025/10/13 4:15:41

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容

目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法&#xff0c;当前调用一个医疗行业的AI识别算法后返回…...

编程新知 2026/2/9 17:11:06

AspectJ 在 Android 中的完整使用指南

一、环境配置&#xff08;Gradle 7.0 适配&#xff09; 1. 项目级 build.gradle // 注意&#xff1a;沪江插件已停更&#xff0c;推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

编程新知 2025/7/7 22:33:57

为什么要创建 Vue 实例

核心原因：Vue 需要一个「控制中心」来驱动整个应用 你可以把 Vue 实例想象成你应用的**「大脑」或「引擎」。它负责协调模板、数据、逻辑和行为，将它们变成一个活的、可交互的应用**。没有这个实例，你的代码只是一堆静态的 HTML、JavaScript 变量和函数，无法「活」起来。 …...

编程新知 2026/2/9 7:06:29

Kafka主题运维全指南：从基础配置到故障处理

#作者&#xff1a;张桐瑞 文章目录 主题日常管理1. 修改主题分区。2. 修改主题级别参数。3. 变更副本数。4. 修改主题限速。5.主题分区迁移。6. 常见主题错误处理常见错误1&#xff1a;主题删除失败。常见错误2&#xff1a;__consumer_offsets占用太多的磁盘。 主题日常管理 …...

编程新知 2025/6/10 21:14:43

实战三：开发网页端界面完成黑白视频转为彩色视频

​一、需求描述 设计一个简单的视频上色应用&#xff0c;用户可以通过网页界面上传黑白视频&#xff0c;系统会自动将其转换为彩色视频。整个过程对用户来说非常简单直观&#xff0c;不需要了解技术细节。 效果图 ​二、实现思路 总体思路&#xff1a; 用户通过Gradio界面上…...

编程新知 2026/2/5 5:03:25