【数学】CF1514 C
Problem - 1514C - Codeforces
题意:

思路:

Code:
#include <bits/stdc++.h>using i64 = long long;constexpr int N = 2e5 + 10;
constexpr int M = 2e5 + 10;
constexpr int mod = 998244353;void solve() {int n;std::cin >> n;std::vector<int> ans;i64 mul = 1ll;for (int i = 1; i <= n - 1; i ++) {if (std::__gcd(i, n) == 1) {ans.push_back(i);mul *= i;mul %= n;}}if (mul == 1ll) {std::cout << ans.size() << "\n";for (int i = 0; i < ans.size(); i ++) {std::cout << ans[i] << " \n" [i == ans.size() - 1];}}else {std::cout << ans.size() - 1 << "\n";for (int i = 0; i < ans.size() - 1; i ++) {if (ans[i] != n) {std::cout << ans[i] << " "; }}std::cout << "\n";}
}
signed main() {std::ios::sync_with_stdio(false);std::cin.tie(nullptr);int t = 1;while(t --) {solve();}return 0;
}
相关文章:

【数学】CF1514 C
Problem - 1514C - Codeforces 题意: 思路: Code: #include <bits/stdc.h>using i64 long long;constexpr int N 2e5 10; constexpr int M 2e5 10; constexpr int mod 998244353;void solve() {int n;std::cin >> n;std:…...

SqlServer基础之(触发器)
概念: 触发器(trigger)是SQL server 提供给程序员和数据分析员来保证数据完整性的一种方法,它是与表事件相关的特殊的存储过程,它的执行不是由程序调用,也不是手工启动,而是由事件来触发&#x…...
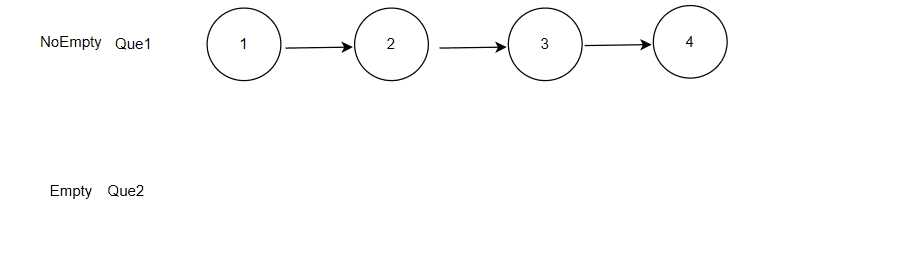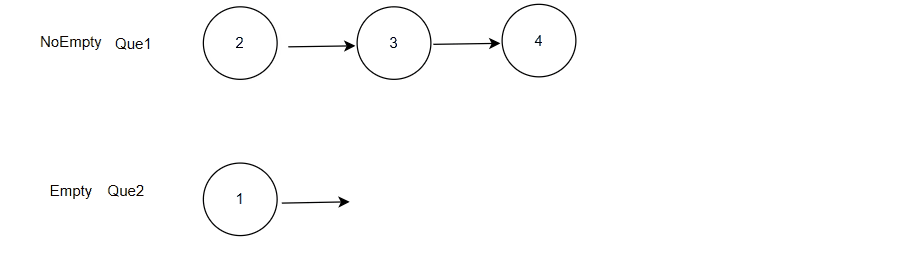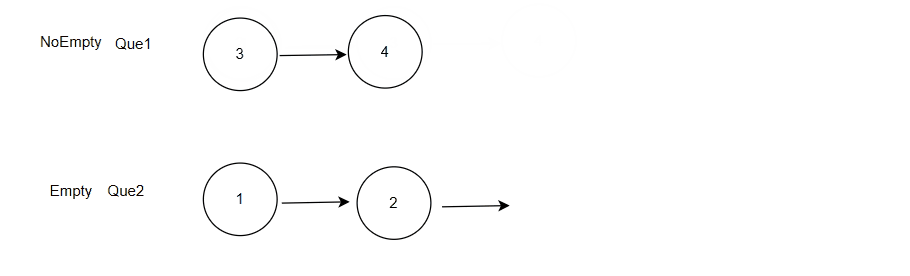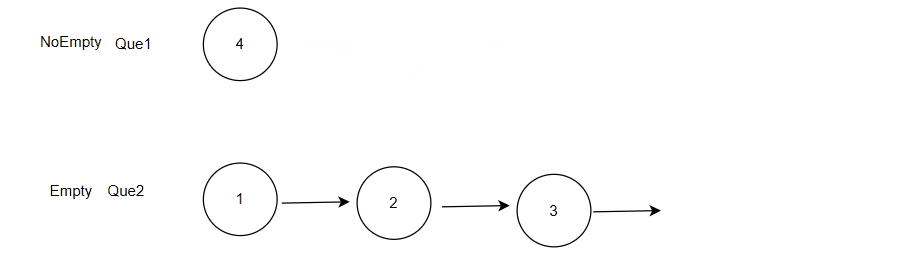
数据结构刷题训练:队列实现栈
目录 前言 1. 题目:使用队列实现栈 2. 思路 3. 分析 3.1 创建栈 3.2入栈 3.3 出栈 3.4 栈顶数据 3.5 判空和 “ 栈 ” 的销毁 4. 题解 总结 前言 我们已经学习了栈和队列,也都实现了它们各自的底层接口,那么接下我们就要开始栈和队列的专项刷…...

(统计学习方法|李航)第四章 朴素贝叶斯算法——贝叶斯估计
贝叶斯估计方法: 计算男女时只有两个值,所以K2 贝叶斯估计就是拉普拉斯平滑 估计方法:为什么叫做贝叶斯估计呢? 例题: 重新回顾以下朴素贝叶斯: 对他求导,求出最大值 得到了色i他的估计值&…...

企业直播MR虚拟直播(MR混合现实直播技术)视频介绍
到底什么是企业直播MR虚拟直播(MR混合现实直播技术)? 企业直播MR虚拟直播新玩法(MR混合现实直播技术) 我的文章推荐: [视频图文] 线上研讨会是什么,企业对内对外培训可以用线上研讨会吗&#x…...

React Fiber: 从 Reconciliation 到 Concurrent Mode
React Fiber 是 React 中的一种新的协调算法,它的主要目的是提高 React 的性能和可维护性。在 React Fiber 之前,React 使用了一种叫做 Stack Reconciliation 的算法来处理组件的更新和渲染。但是 Stack Reconciliation 存在一些问题,比如无法…...
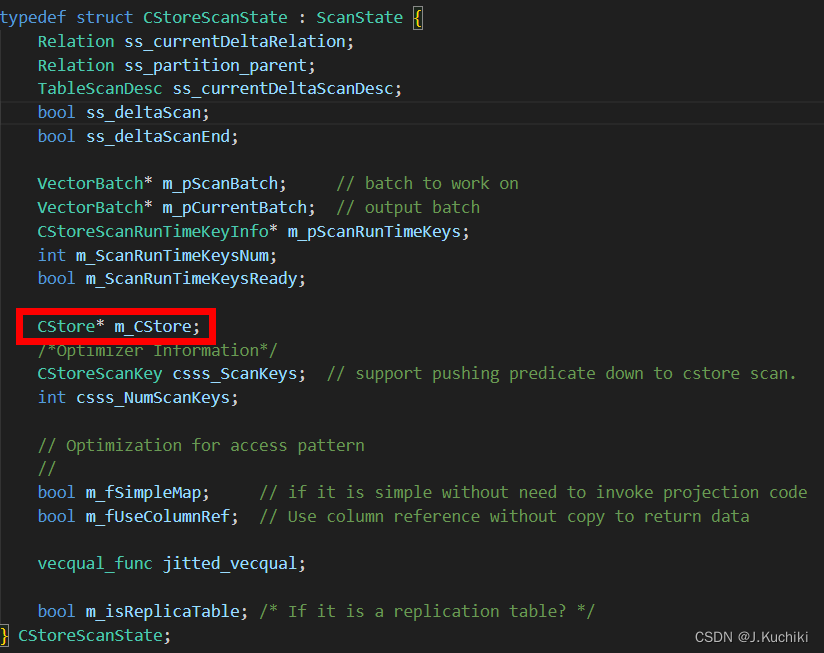
【PostgreSQL内核学习(十一)—— OpenGauss源码学习(CopyTo)】
可优化语句执行 概述什么是列存储?列存的优势 相关函数CopyToCStoreCopyToCopyStatetupleDescCStoreScanDesc CStoreBeginScanRelationSnapshotProjectionInfo GetCStoreNextBatchRunScanFillVecBatchCStoreIsEndScan CStoreEndScan 声明:本文的部分内容…...
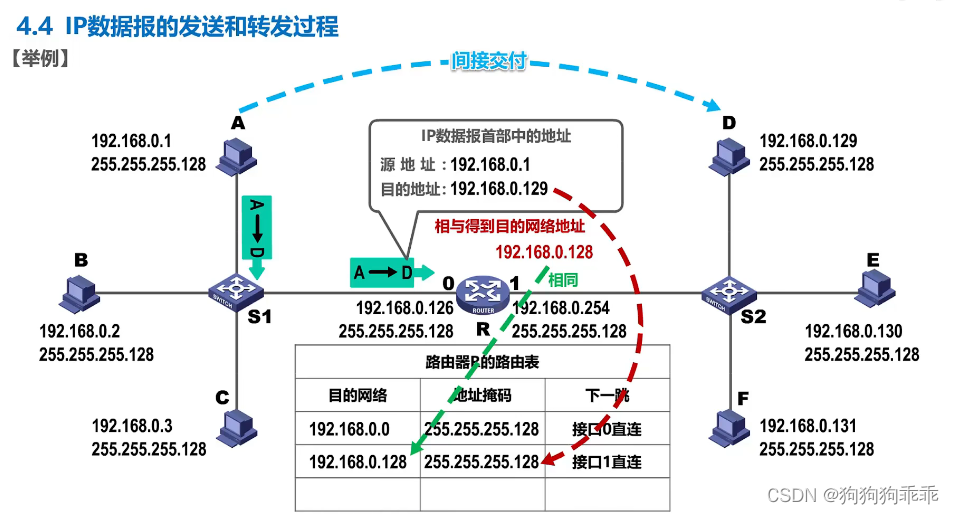
计算机网络 网络层 IPv4地址
A类地址第一位固定0 B类10 其下同理...

【程序员社交】多和高层次人群交流
定义问题:如何多和高层次人群交流获取经验提升自己? 收集信息:通过社交媒体、行业论坛、行业大会等途径获取高层次人群的信息和观点,并了解他们的工作经历、技能和能力。 分析信息:分析收集到的信息,了解…...

机器学习笔记 - 基于C++的深度学习 三、实现成本函数
机器学习中的建模 作为人工智能工程师,我们通常将每个任务或问题定义为一个函数。 例如,如果我们正在开发面部识别系统,我们的第一步是将问题定义为将输入图像映射到标识符的函数F(X)。但是问题是如何知道F(X)公式? 事实上,使用公式或一系列固有规则来定义F(X)是不可行的(…...

lazada、shopee店铺如何利用测评提高权重和排名?
在 lazada、shopee平台上开店后,卖家们必须对店铺的权重进行更多的关注。如果店铺的权重越高,那么它就会带来更多的流量和更多的订单,那么在 lazada、shopee平台上开设一家店铺,该怎样增加它的店铺权重和排名呢? laza…...

安全第二次
一,iframe <iframe>标签用于在网页里面嵌入其他网页。 1,sandbox属性 如果嵌入的网页是其他网站的页面,因不了解对方会执行什么操作,因此就存在安全风险。为了限制<iframe>的风险,HTML 提供了sandb…...

125、SpringBoot可以同时处理多少请求?
SpringBoot可以同时处理多少请求? 一、前言二、线程池4大参数图解三、代码示例一、前言 我们都知道,SpringBoot默认的内嵌容器是Tomcat,也就是我们的程序实际上是运行在Tomcat里的。所以与其说SpringBoot可以处理多少请求,到不如说Tomcat可以处理多少请求。 关于Tomcat的默…...
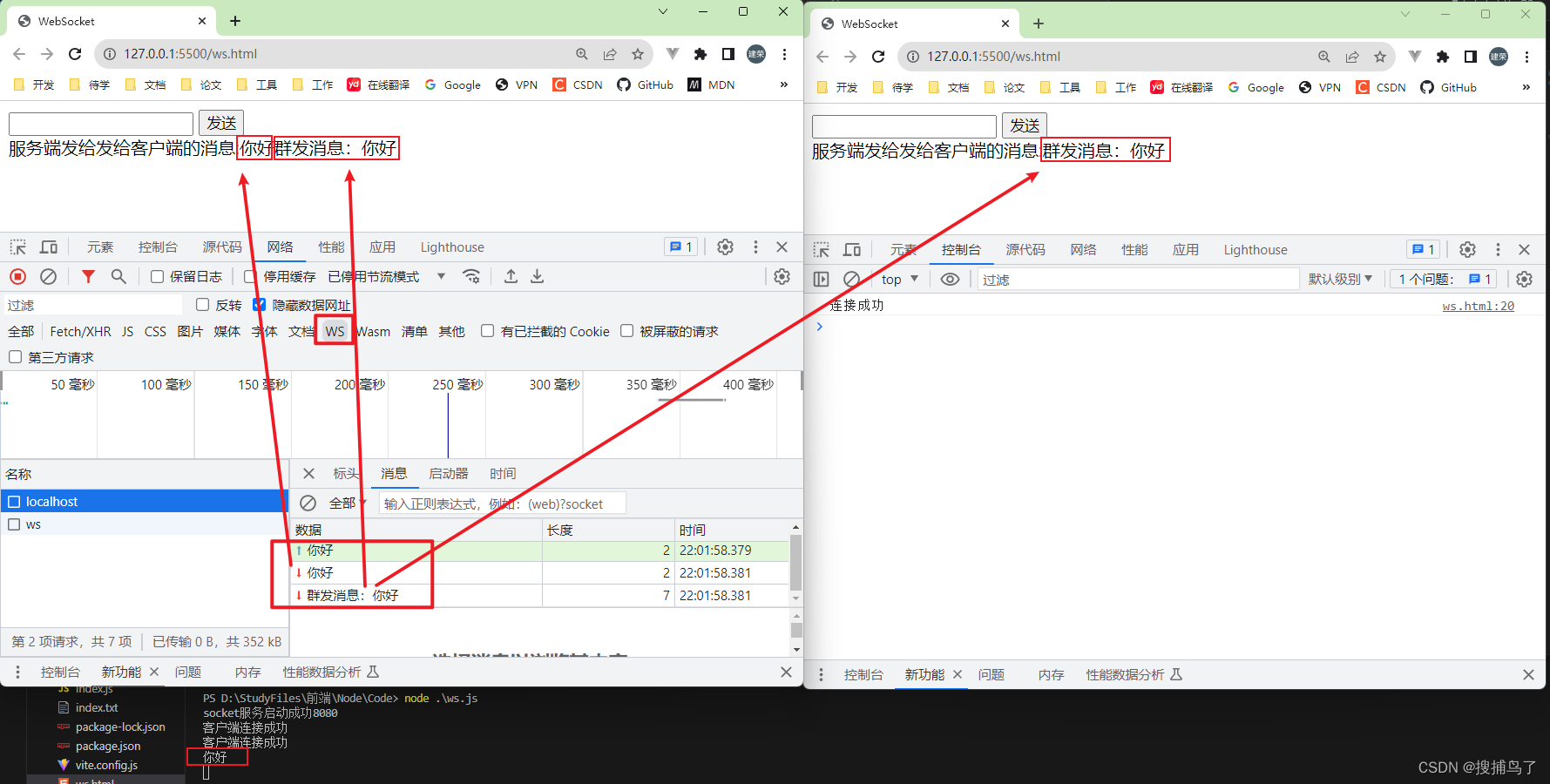
SSE技术和WebSocket技术实现即时通讯
文章目录 一、SSE1.1 什么是SSE1.2 工作原理1.3 特点和适用场景1.4 API用法1.5 代码实现 二、WebSocket2.1 什么是WebSocket2.2 工作原理2.3 特点和适用场景2.4 API用法2.5 代码实现2.6 心跳检测 三、SSE与WebSocket的比较 当涉及到实现实时通信的Web应用程序时,两种…...

什么是敏捷开发?
敏捷开发流程:制度化、规范化地PUA程序员的顶级神器!!!...

tcp发送整型,结构体等数据的方法
测试环境 Receiver: x86 UbuntuSender: arm64 android 发送整型数 C语言和套接字库来发送一个整型变量(int)的客户端程序。 它首先创建一个TCP套接字,然后连接到指定的服务器地址和端口。接着,它将一个整型变量(in…...

【Unity每日一记】让一个物体按余弦曲线移动—(三角函数的简单运用)
👨💻个人主页:元宇宙-秩沅 👨💻 hallo 欢迎 点赞👍 收藏⭐ 留言📝 加关注✅! 👨💻 本文由 秩沅 原创 👨💻 收录于专栏:uni…...

python爬虫实战——数据可视化
本篇文章将介绍如何利用Python爬虫获取数据并进行可视化展示,包括以下主要内容: 数据获取:使用requests库发送HTTP请求获取目标网页的数据;数据解析:使用BeautifulSoup库对HTML代码进行解析提取所需数据;数…...
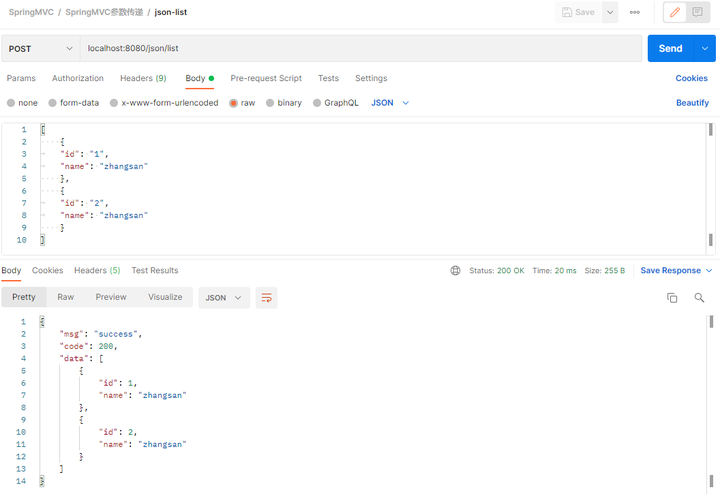
案例13 Spring MVC参数传递案例
基于Spring MVC实现HttpServletRequest、基本数据类型、Java Bean、数组、List、Map、JSON方式的参数传递。 1. 创建项目 选择Maven快速构建web项目,项目名称为case13-springmvc02。 2. 配置Maven依赖 <?xml version"1.0" encoding"UTF-8&quo…...
IntellIJ Idea 连接数据库-MySql
前言:可以用mariaDB工具,在本地创建服务器主机和数据库,而后用intellIJ Idea尝试连接 MariaDB创建数据库练习 1.IntellIJ Idea打开界面右侧Database工具,选择MySQL数据库。 2.填写数据库账号密码,地址端口号ÿ…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...
