网络防御(6)
密码学综合应用
定义:
密码学综合应用是指将密码学的理论和技术应用于各种场景中,以保障信息的安全性、完整性和可靠性。密码学的应用范围非常广泛,包括通信安全、网络安全、电子商务、数字签名、认证、密钥管理等。
密码学综合应用的实例:
1. 加密通信:使用对称加密(如AES)或非对称加密(如RSA)对数据进行加密,确保在传输过程中的数据安全。例如,HTTPS协议就使用了SSL/TLS加密来保护网络传输的数据。
2. 数字签名:使用数字签名技术(如DSA、ECDSA等)对文件或数据进行签名,以验证数据的完整性和来源。例如,GPG和S/MIME协议就采用了数字签名技术来保障邮件的安全。
3. 认证和授权:利用密码学原理实现身份认证和权限控制。例如,Kerberos协议、OAuth 2.0等协议提供了认证和授权机制,用于保护系统的安全性。
4. 密钥管理:密钥管理是密码学应用中的一个重要环节。通过密钥管理系统(如KMS)对密钥进行生成、分发、存储和销毁,确保密钥的安全性。
5. 零知识证明:零知识证明是一种密码学协议,允许一方向另一方证明某个陈述是正确的,而无需透露任何其他信息。例如,Zcash和ZK-SNARKs等协议就利用了零知识证明技术来保护用户隐私。
6. 密码学应用在区块链:区块链技术中的加密算法(如SHA-256、ECC等)和共识机制(如工作量证明PoW、权益证明PoS等)都有密码学的影子,它们共同保证了区块链的安全、透明和不可篡改。
7. 隐私保护:密码学技术在隐私保护领域有广泛应用,如差分隐私、同态加密、多方计算等。这些技术在保护数据隐私的同时,允许对数据进行分析和处理。
相关文章:
)
网络防御(6)
密码学综合应用 定义: 密码学综合应用是指将密码学的理论和技术应用于各种场景中,以保障信息的安全性、完整性和可靠性。密码学的应用范围非常广泛,包括通信安全、网络安全、电子商务、数字签名、认证、密钥管理等。 密码学综合应用的实例…...
内嵌变量)
【Nginx15】Nginx学习:HTTP核心模块(十二)内嵌变量
Nginx学习:HTTP核心模块(十二)内嵌变量 关于内嵌变量,其实就是 Nginx 开放给我们的在配置文件中可以使用的变量。源码中无非就是替换成真实的代码变量进行操作。这些变量可以帮助我们做很多事情。之前的文章中其实也有不少地方用到…...

2023年中国HPV宫颈癌疫苗需求量、竞争格局、市场规模及行业细分产品规模分析[图]
HPV宫颈癌疫苗也是人乳头瘤病毒疫苗,由重组表达的HPV主要衣壳蛋白L1病毒样颗粒制备而成,可以预防由HPV感染及其引起的各种疾病,包括宫颈癌、阴道癌、肛门癌和口咽癌等癌症,及相关癌前病变。 目前中国在售的HPV疫苗包括万泰生物的二…...

基于LMK2572的FPGA逻辑实现
项目背景: 在时钟同步或类似时钟方案系统,需要用到一些时钟芯片,LMK2572就是一款频率带宽覆盖广的芯片。 项目介绍: LMK2572该器件是一个低功耗、高性能的宽带合成器,可生成 13MHz 到 6.4GHz 的任何频率,而无需使用内部倍频器。该 PLL 可提供优异的性能,而 3.3V 单电源…...
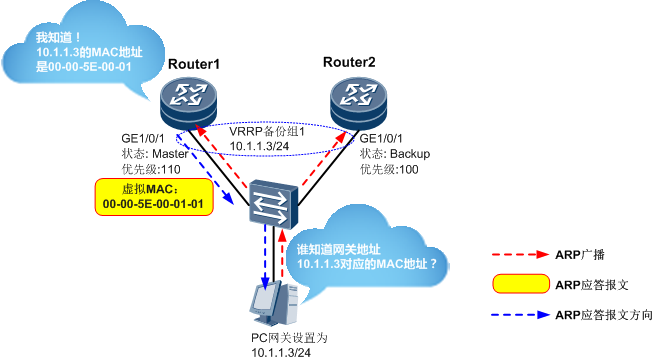
数据通信——VRRP
引言 之前把实验做了,结果发现我好像没有写过VRRP的文章,连笔记都没记过。可能是因为对STP的记忆,导致现在都没忘太多。 一,什么是VRRP VRRP全名是虚拟路由冗余协议,虚拟路由,看名字就知道这是运行在三层接…...

第二章:CSS基础进阶-part2:CSS过渡与动画
文章目录 CSS3 过渡动画一、transition属性二、transform属性-2D变换2.1 tanslate : 移动2.2 rotate-旋转2.3 scale-变形2.4 skew-斜切2.5 transform-origin: 变换中心点设置 三、CSS3关键帧动画四、CSS3-3D变换4.1 perspective 定义3D元素距视图距离4.2 transform-…...

华为OD真题---玩牌高手--带答案
2023华为OD统一考试(AB卷)题库清单-带答案(持续更新)or2023年华为OD真题机考题库大全-带答案(持续更新) 玩牌高手 给定一个长度为n的整型数组,表示一个选手在n轮内可选择的牌面分数。选手基于规…...
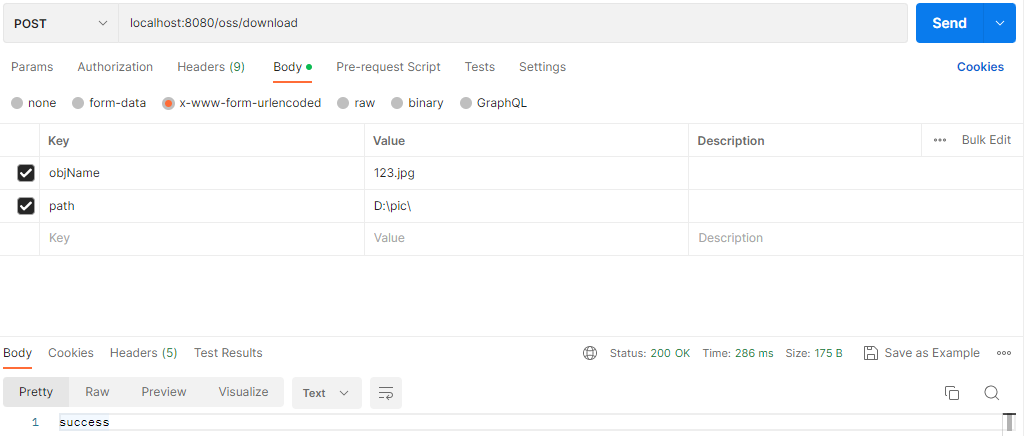
案例14 Spring MVC文件上传案例
基于Spring MVC实现文件上传: 使用commons-fileupload实现上传文件到本地目录。 实现上传文件到阿里云OSS和从阿里云OSS下载文件到本地。 1. 创建项目 选择Maven快速构建web项目,项目名称为case14-springmvc03。 2. 配置Maven依赖 <?xml ver…...

如何用Python实现多线程
1 问题 线程是操作系统能够进行运算调度的最小单位。进程被包含在进程中,是进程中实际处理单位。一条线程就是一堆指令集合。一条线程是指进程中一个单一顺序的控制流,一个进程中可以并发多个线程,每条线程并行执行不同的任务。那么如何用pyt…...

Chrome浏览器导出插件并安装到其他电脑浏览器上的解决方案
大家好,我是爱编程的喵喵。双985硕士毕业,现担任全栈工程师一职,热衷于将数据思维应用到工作与生活中。从事机器学习以及相关的前后端开发工作。曾在阿里云、科大讯飞、CCF等比赛获得多次Top名次。现为CSDN博客专家、人工智能领域优质创作者。喜欢通过博客创作的方式对所学的…...

对话即数据分析,网易数帆ChatBI做到了
大数据产业创新服务媒体 ——聚焦数据 改变商业 在当今数字化快速发展的时代,数据已经成为业务经营与管理决策的核心驱要素。无论是跨国大企业还是新兴创业公司,正确、迅速地洞察数据已经变得至关重要。然而,传统的BI工具往往对用户有一定的…...
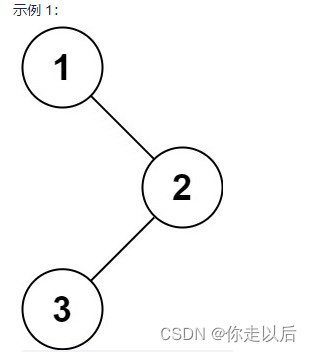
简单记录牛客top101算法题(初级题C语言实现)BM17 二分查找 BM21 旋转数组的最小数字 BM23 二叉树的前序遍历
1. BM17 二分查找 要求:给定一个 元素升序的、无重复数字的整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标(下标从 0 开始),否则返回 -1。 输入:…...

日常BUG——Java使用Bigdecimal类型报错
😜作 者:是江迪呀✒️本文关键词:日常BUG、BUG、问题分析☀️每日 一言 :存在错误说明你在进步! 一、问题描述 直接上代码: Test public void test22() throws ParseException {System.out.p…...
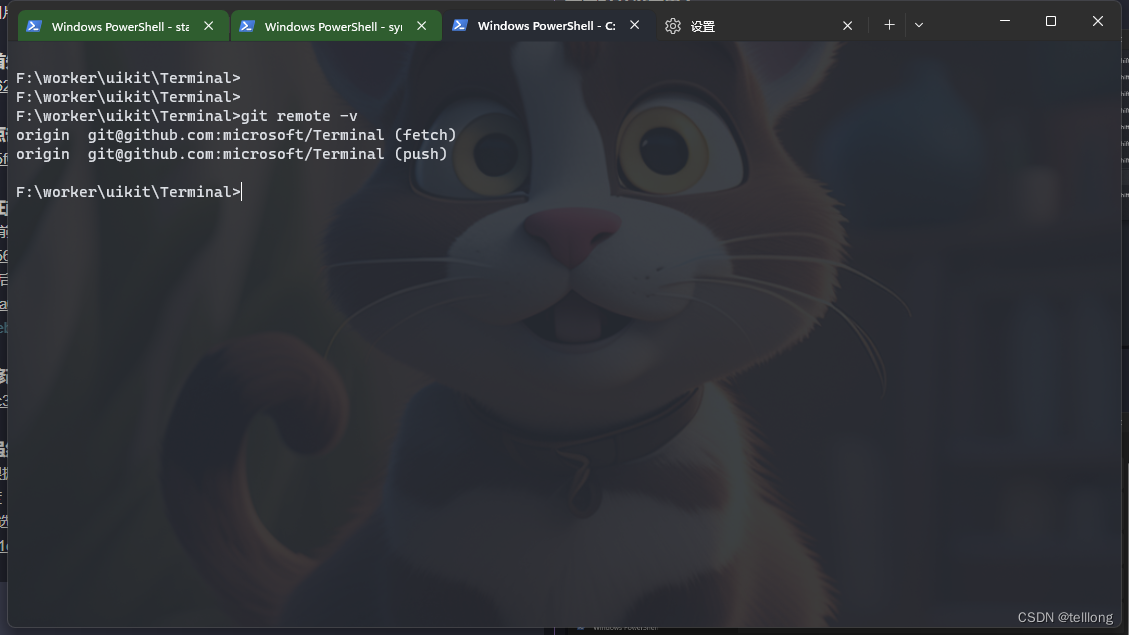
为Windows Terminal设置背景图片
直接通过界面上选项无法达到修改背景图片的目的,后再在官网,和git上找到通过修改配置文件来更改背景图片 首先打开设置界面 点击左下角打开settings.json文件 在json中profiles关键字default选项相面增加几个key,就像下面 修改前修改后 修改后的termin…...
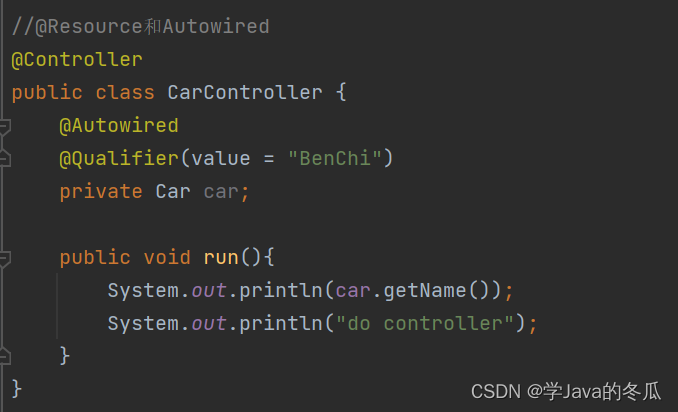
【Spring】-Spring中Bean对象的存取
作者:学Java的冬瓜 博客主页:☀冬瓜的主页🌙 专栏:【Framework】 主要内容:往spring中存储Bean对象的三大方式:XML方式(Bean标签);五大类注解;方法注解。从spring中取对象的两种方式…...

机器人CPP编程基础-03变量类型Variables Types
机器人CPP编程基础-02变量Variables 全文AI生成。 C #include<iostream>using namespace std;main() {int a10,b35; // 4 bytescout<<"Value of a : "<<a<<" Address of a : "<<&a <<endl;cout<<"Val…...

或许有用的开源项目平台——物联网、区块链、商城、CMS、客服系统、低代码、可视化、ERP等
摘自个人印象笔记Evernote Export wumei-smart-物美智能开源物联网平台 官网:https://wumei.live/ gitee:https://gitee.com/kerwincui/wumei-smart 一个简单易用的物联网平台。可用于搭建物联网平台以及二次开发和学习。适用于智能家居、智慧办公、智慧…...
火车头采集伪原创插件【php源码】
大家好,小编来为大家解答以下问题,python代码大全和用法,python代码大全简单,现在让我们一起来看看吧! 火车头采集ai伪原创插件截图: 1、题目:列表转换为字典。 程序源代码: 1 #!/us…...

【数学】CF1514 C
Problem - 1514C - Codeforces 题意: 思路: Code: #include <bits/stdc.h>using i64 long long;constexpr int N 2e5 10; constexpr int M 2e5 10; constexpr int mod 998244353;void solve() {int n;std::cin >> n;std:…...

SqlServer基础之(触发器)
概念: 触发器(trigger)是SQL server 提供给程序员和数据分析员来保证数据完整性的一种方法,它是与表事件相关的特殊的存储过程,它的执行不是由程序调用,也不是手工启动,而是由事件来触发&#x…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

MacOS下Homebrew国内镜像加速指南(2025最新国内镜像加速)
macos brew国内镜像加速方法 brew install 加速formula.jws.json下载慢加速 🍺 最新版brew安装慢到怀疑人生?别怕,教你轻松起飞! 最近Homebrew更新至最新版,每次执行 brew 命令时都会自动从官方地址 https://formulae.…...
