探索FSM (有限状态机)应用
有限状态机(FSM) 是计算机科学中的一种数学模型,可用于表示和控制系统的行为。它由一组状态以及定义在这些状态上的转换函数组成。FSM 被广泛用于计算机程序中的状态机制。
有限状态机(FSM)应用场景
-
在各种自动化系统的应用: 例如交通信号灯、地铁站的旋转闸门、银行自动取款机等。通过对状态和转换函数的定义,可以实现对系统行为的精确控制。
交通信号灯状态流转图

地铁站的旋转闸门状态流转图

银行自动取款机状态流转图
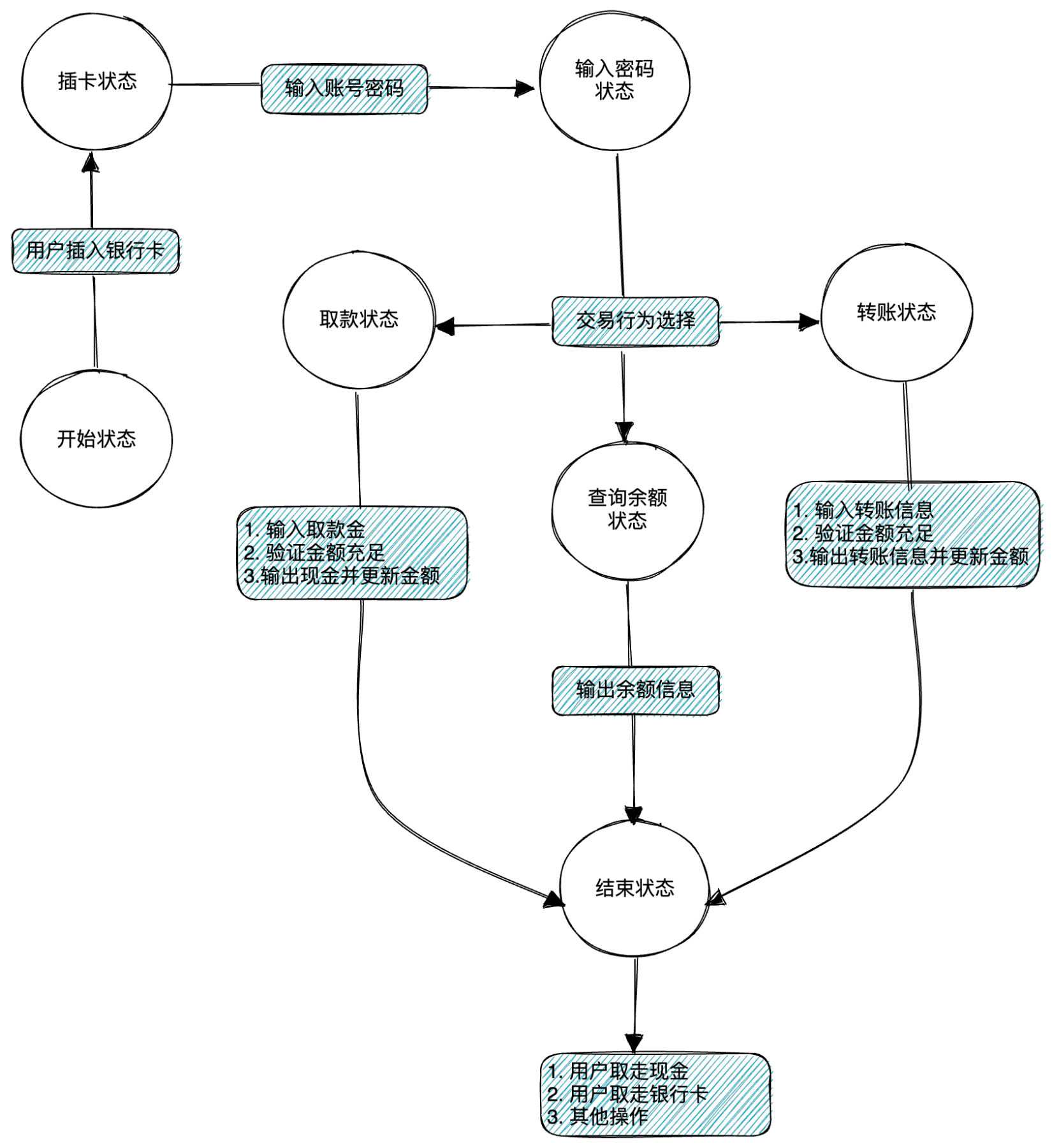
-
在编程领域的应用: 例如在编写编译器和解释器时,可以使用有限状态机(FSM) 来处理词法分析。例如:
JSON.Parse -
在Notion中应用: 可以使用 有限状态机(FSM) 的相关概念来构建各种工作流程,例如状态转换图、状态转换表等。
-
在web中应用: 我们熟悉的 Promise 也是一个状态机,具有三个状态:pending、resolved。rejected。
Promise状态流转图

登录功能流转图
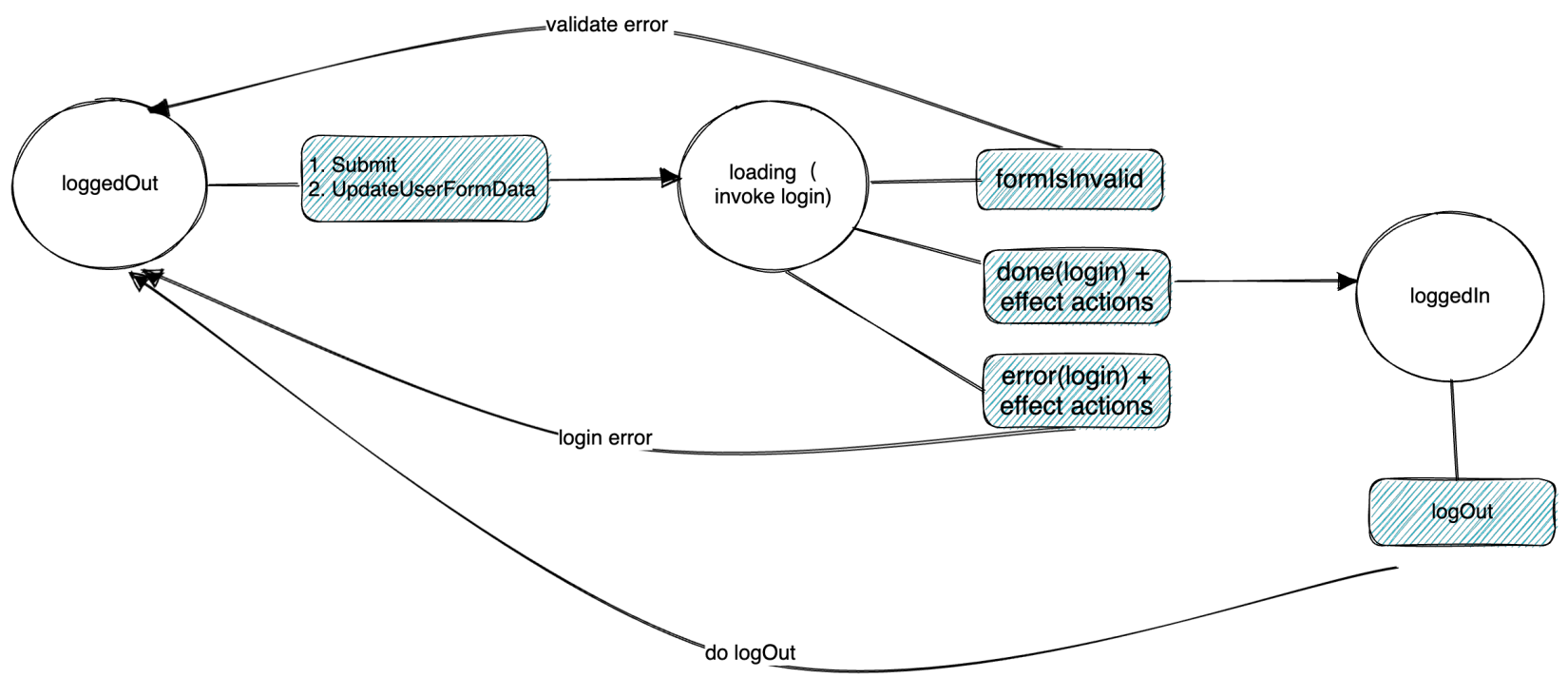
类似这样的状态机的例子数不胜数,甚至于,人也是一种极其复杂的状态机,给定一种刺激或多种刺激组合,也会触发人从某种状态过渡到另一种状态。只不过复杂程度极高,以至于现代科学完全无法解密这种状态机。
有限状态机(FSM)实现原理
具体来说,FSM由以下几部分组成:
- 初始状态:系统的初始状态。
- 状态集合:表示系统可能处于的各种状态。
- 转移函数:定义系统在不同状态之间的转移条件和结果。
- 终止状态:系统在某个状态下可以停止计算。
有限状态机(FSM) 的实现基于状态转移图。状态转移图 是一个有向图,它表示有限状态机(FSM) 中状态之间的转移关系。在状态转移图中,每个状态表示系统的某种状态,每个转移表示系统从一个状态转移到另一个状态的条件和结果。
实现简易的有限状态机(FSM)
实现步骤
- 当状态机开始执行时,它会自动进入初始化状态(initial state)。
- 每个状态都可以定义,在进入(onEnter)或退出(onExit)该状态时发生的行为事件(actions),通常这些行为事件会携带副作用(side effect)。
- 每个状态都可以定义触发转换(transition)的事件。
- 转换定义了在退出一个状态并进入另一个状态时,状态机该如何处理这种事件。
- 在状态转换发生时,可以定义可以触发的行为事件,从而一般用来表达其副作用。
状态转移图

function createMachine(stateMachineDefinition) {const machine = {value: stateMachineDefinition.initialState,performTransition(currentState, event) {const currentStateDefinition = stateMachineDefinition[currentState];const destinationTransition = currentStateDefinition.transitions[event];if (!destinationTransition) {return;}const destinationState = destinationTransition.target;const destinationStateDefinition =stateMachineDefinition[destinationState];destinationTransition.action();currentStateDefinition.actions.onExit();destinationStateDefinition.actions.onEnter();machine.value = destinationState;return machine.value;},};return machine;
}const machine = createMachine({initialState: "off",off: {actions: {onEnter() {console.log("off: onEnter");},onExit() {console.log("off: onExit");},},transitions: {switch: {target: "on",action() {console.log('transition action for "switch" in "off" state');},},},},on: {actions: {onEnter() {console.log("on: onEnter");},onExit() {console.log("on: onExit");},},transitions: {switch: {target: "off",action() {console.log('transition action for "switch" in "on" state');},},},},
});let state = machine.value;
console.log(`current state: ${state}`);
state = machine.performTransition(state, "switch");
console.log(`current state: ${state}`);
state = machine.performTransition(state, "switch");
console.log(`current state: ${state}`);有限状态机(FSM)的 应用实现
在状态比较多的情况下,把状态、事件及 transitions 集中到一个状态机中,进行统一管理。这样不需要写太多的 if-else,或者 case 判断,如果增加状态和事件,也便于代码的维护和扩展。
文本解析器
实现思路
- 确定状态和输入
在编写 FSM 之前,我们需要确定我们的状态和输入。在这个例子中,我们将定义三个状态:起始状态、数字状态和字符串状态。我们还将定义四个输入:数字、字母、引号和空格。 - 定义状态机类
现在,我们可以编写代码来实现我们的 FSM 。我们需要定义一个状态机类,它将接受输入,并根据转移规则转换状态。该类应该包含以下属性:currentState:当前状态。states:状态列表。transitions:转移列表。
它还应该包含以下方法:transition:该方法接受一个输入参数input,根据当前状态以及输入参数,执行相应的状态转换。
- 定义转移规则
我们还需要定义状态之间的转移规则。为此,我们将使用转移列表,其中包含状态之间的映射和输入。转移规则应该考虑当前状态和输入,并根据它们确定下一个状态。如果当前状态和输入没有匹配的转移规则,则应该抛出一个异常。 - 解析文本
现在,我们可以使用状态机解析文本。我们需要将文本拆分为单词,并将每个单词作为输入提供给状态机。在处理完所有输入后,我们可以通过调用getInputType方法来获取解析的令牌。
示例代码
const STATES = {START: "start",NUMBER: "number",STRING: "string",
};const INPUTS = {NUMBER: "number",LETTER: "letter",SPACE: "space",QUOTE: "quote",
};const TRANSITIONS = [{currentState: STATES.START,input: INPUTS.NUMBER,nextState: STATES.NUMBER,},{currentState: STATES.START,input: INPUTS.LETTER,nextState: STATES.STRING,},{ currentState: STATES.START, input: INPUTS.SPACE, nextState: STATES.START },{ currentState: STATES.START, input: INPUTS.QUOTE, nextState: STATES.STRING },{currentState: STATES.NUMBER,input: INPUTS.NUMBER,nextState: STATES.NUMBER,},{ currentState: STATES.NUMBER, input: INPUTS.SPACE, nextState: STATES.START },{currentState: STATES.STRING,input: INPUTS.LETTER,nextState: STATES.STRING,},{ currentState: STATES.STRING, input: INPUTS.SPACE, nextState: STATES.START },{ currentState: STATES.STRING, input: INPUTS.QUOTE, nextState: STATES.START },
];class TextParse {constructor() {this.currentState = STATES.START;this.buffer = "";this.type;}performTransition(input) {const transition = TRANSITIONS.find((t) => t.currentState === this.currentState && t.input === input.type);if (!transition)throw new Error(`Invalid input "${input.value}" for state "${this.currentState}"`);this.currentState = transition.nextState;if (this.currentState === STATES.START) {const token = this.buffer;const type = this.type;this.buffer = "";this.type = "";return {type,value: token,};} else {this.buffer += input.value;this.type = input.type;}}
}function textParse(input) {const textParse = new TextParse();const tokens = [];for (let i = 0; i < input.length; i++) {const char = input[i];try {const token = textParse.performTransition({type: getInputType(char),value: char,});if (token) {tokens.push(token);}} catch (e) {console.error(e.message);return null;}}const lastToken = textParse.performTransition({ type: INPUTS.SPACE });if (lastToken) {tokens.push(lastToken);}return tokens;
}function getInputType(char) {if (/[0-9]/.test(char)) {return INPUTS.NUMBER;} else if (/[a-zA-Z]/.test(char)) {return INPUTS.LETTER;} else if (/[\s\n\t\r]/.test(char)) {return INPUTS.SPACE;} else if (char === '"') {return INPUTS.QUOTE;} else {throw new Error(`Unknown input type for "${char}"`);}
}// Example usage:
console.log(textParse('123 abc "def ghi" 456'));
// [
// { type: 'number', value: '123' },
// { type: 'letter', value: 'abc' },
// { type: 'letter', value: '"def' },
// { type: 'letter', value: 'ghi' },
// { type: '', value: '' },
// { type: 'number', value: '456' }
// ]
示例代码
web 应用
使用 有限状态机(FSM) 结合 React 构建 web 应用,不局限于身份认证,登录,步骤表单,有蛮多 web 应用在
有限状态机(FSM)的实践 ,下面主要描述 从有限状态机(FSM)在服务端拉取数据的状态转移上的应用
-
状态转移图
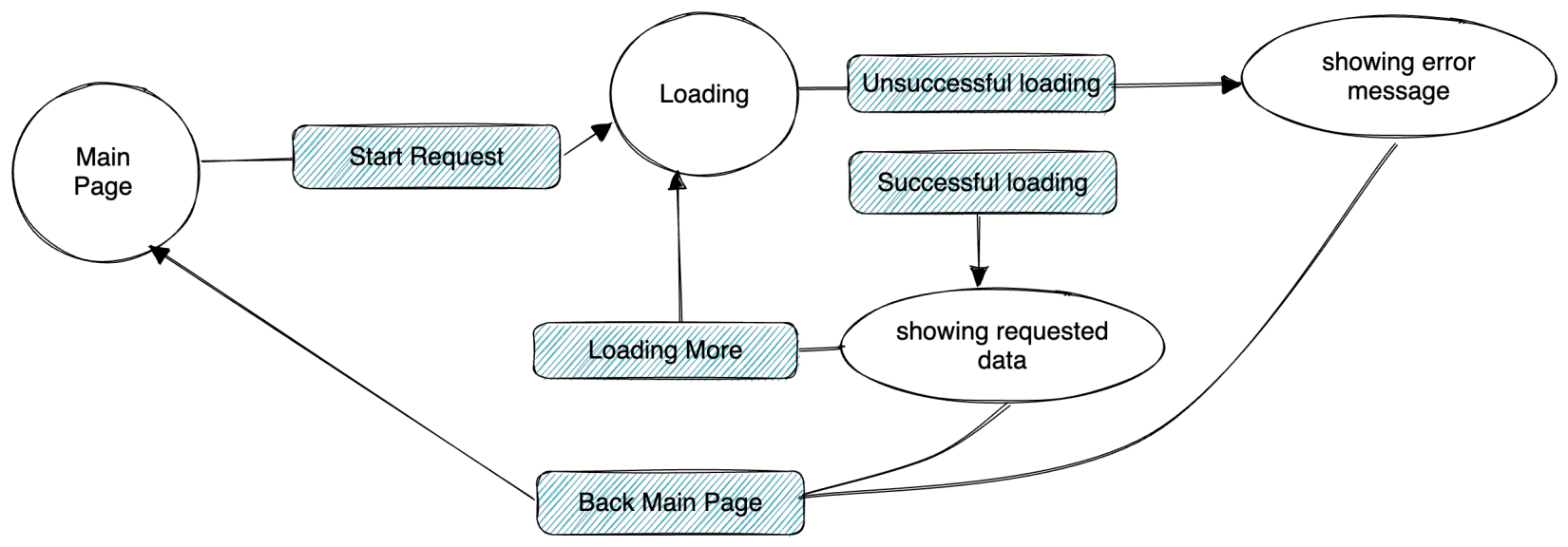
-
状态集(States), 转换规则(Transitions)
const states = {INITIAL: "idle",LOADING: "loading",SUCCESS: "success",FAILURE: "failure",
};
const transitions = {[states.INITIAL]: {fetch: () => /* Returns states.LOADING */,},[states.LOADING]: {},[states.SUCCESS]: {reload: () => /* Returns states.LOADING */,clear: () => /* Returns states.INITIAL */,},[states.FAILURE]: {retry: () => /* Returns states.LOADING */,clear: () => /* Returns states.INITIAL */,},
}
示例代码
总结
结合前端应用的探索体现的不多,可以再作为第二篇内容去探讨,有兴趣的同学可以尝试一下 有限状态机(FSM) 在 web 上的应用探索,以及 Xstate库(FSM封装的功能性库) 的应用,以及跟 状态管理库 差异化的知识。在这里提醒一点,状态管理库 (Redux) 和 Xstate 并不是互斥的,Xstate 关注的是如何设计状态,状态管理库关注的是如何管理状态。事实上,状态机几乎可以与任何无主见的状态管理工具一起使用。我鼓励您探索各种方法,以确定最适合您、您的团队和您的应用程序的方法。
相关文章:

探索FSM (有限状态机)应用
有限状态机(FSM) 是计算机科学中的一种数学模型,可用于表示和控制系统的行为。它由一组状态以及定义在这些状态上的转换函数组成。FSM 被广泛用于计算机程序中的状态机制。 有限状态机(FSM)应用场景 在各种自动化系统…...

6.continue break
6.1continue 关键字 continue 关键字用于立即跳出本次循环,继续下一次循环(本次循环体continue之后的代码会少执行一次)。 例如:吃5个包子,第3个有虫子,就扔掉第3个包子,继续吃第4个第5个包子…...

如何在Linux中强制关闭卡住的PyCharm
在使用PyCharm进行Python开发时,有时可能会遇到卡顿或无响应的情况。当PyCharm卡住时,我们需要强制关闭它以恢复正常操作。今天,我们将介绍在Linux系统中如何强制关闭PyCharm的几种方法。 1. 使用键盘快捷键 在PyCharm所在的窗口中…...

c# Excel数据的导出与导入
搬运:Datagrideview 数据导出Excel , Exel数据导入 //------------------------------------------------------------------------------------- // All Rights Reserved , Copyright (C) 2013 , DZD , Ltd . //----------------------------------------------------------…...

Kotlin~Mediator中介者模式
概念 创建一个中介来降低对象之间的耦合度,关系”多对多“变为“一对多”。 角色介绍 Mediator:抽象中介者,接口或者抽象类。ConcreteMediator:中介者具体实现,实现中介者接口,定义一个List管理Colleagu…...

石子合并问题
一.试题 在一个园形操场的四周摆放N堆石子(N≤100),现要将石子有次序地合并成一堆。规定 每次只能选相邻的两堆合并成新的一堆,并将新的一堆的石子数,记为该次合并的得分。 编一程序,由文件读入…...

剑指Offer-搜索与回溯算法
文章目录 剑指 Offer 32 - I. 从上到下打印二叉树题意:解:代码: 剑指 Offer 32 - II. 从上到下打印二叉树 II题意:解:代码: 剑指 Offer 32 - III. 从上到下打印二叉树 III题意:解:代…...

【云原生】Docker 详解(三):Docker 镜像管理基础
Docker 详解(三):Docker 镜像管理基础 1.镜像的概念 镜像可以理解为应用程序的集装箱,而 Docker 用来装卸集装箱。 Docker 镜像含有启动容器所需要的文件系统及其内容,因此,其用于创建并启动容器。 Dock…...
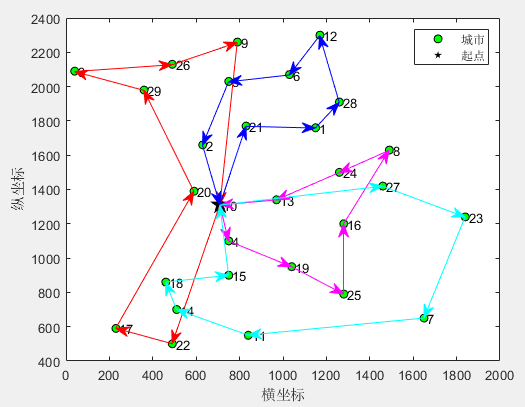
SD-MTSP:蜘蛛蜂优化算法SWO求解单仓库多旅行商问题MATLAB(可更改数据集,旅行商的数量和起点)
一、蜘蛛蜂优化算法SWO 蜘蛛蜂优化算法(Spider wasp optimizer,SWO)由Mohamed Abdel-Basset等人于2023年提出,该算法模型雌性蜘蛛蜂的狩猎、筑巢和交配行为,具有搜索速度快,求解精度高的优势。蜘蛛蜂优化算…...
) 使用】)
【ARM 嵌入式 编译系列 3.1 -- GCC __attribute__((used)) 使用】
文章目录 __attribute__((used)) 属性介绍代码演示编译与输出GCC 编译选项 上篇文章:ARM 嵌入式 编译系列 3 – GCC attribute((weak)) 弱符号使用 下篇文章:ARM 嵌入式 编译系列 3.2 – glibc 学习 __attribute__((used)) 属性介绍 在普通的 C/C 程序中…...
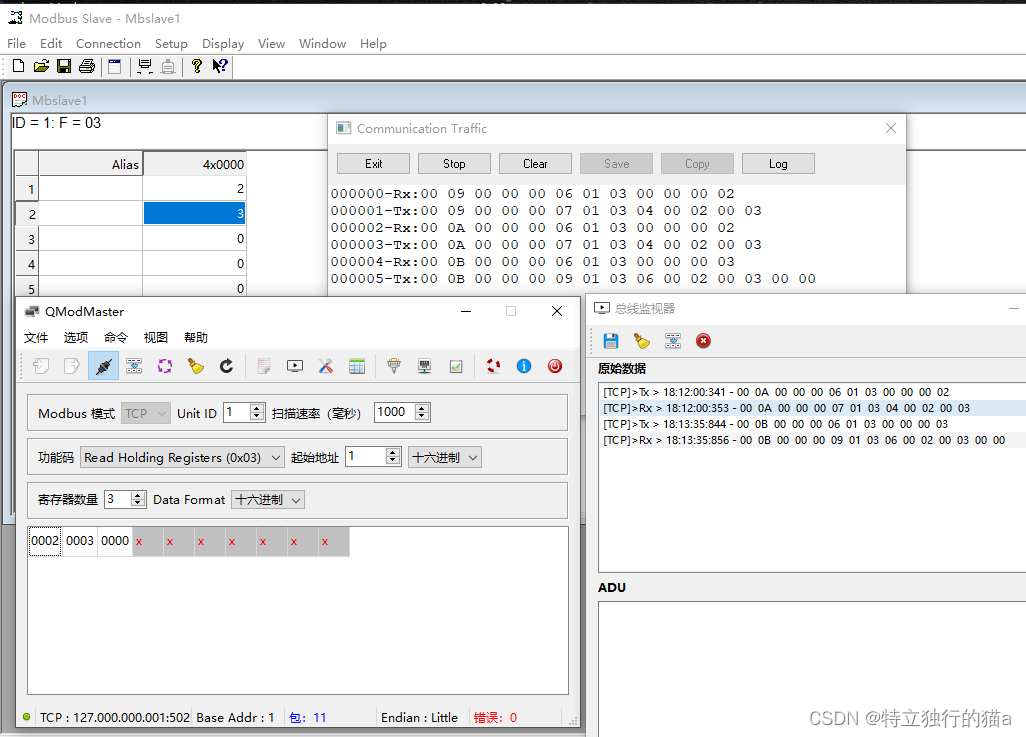
C++ ModBUS TCP客户端工具 qModMaster 介绍及使用
qModMaster工具介绍 QModMaster是一个基于Qt的Modbus主站(Master)模拟器,用于模拟和测试Modbus TCP和RTU通信。它提供了一个直观的图形界面,使用户能够轻松设置和发送Modbus请求,并查看和分析响应数据。 以下是QModM…...
笔记本电脑如何把sd卡数据恢复
在使用笔记本电脑过程中,如果不小心将SD卡里面的重要数据弄丢怎么办呢?别着急,本文将向您介绍SD卡数据丢失常见原因和恢复方法。 ▌一、SD卡数据丢失常见原因 - 意外删除:误操作或不小心将文件或文件夹删除。 - 误格式化&#…...

【2023 华数杯全国大学生数学建模竞赛】 B题 不透明制品最优配色方案设计 39页论文及python代码
【2023 华数杯全国大学生数学建模竞赛】 B题 不透明制品最优配色方案设计 39页论文及python代码 1 题目 B 题 不透明制品最优配色方案设计 日常生活中五彩缤纷的不透明有色制品是由着色剂染色而成。因此,不透明制品的配色对其外观美观度和市场竞争力起着重要作用。…...
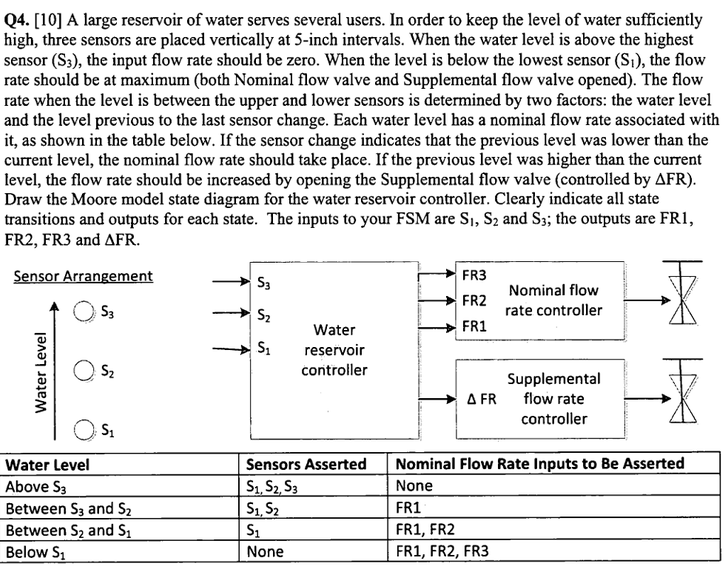
Exams/ece241 2013 q4
蓄水池问题 S3 S2 S1 例如:000 代表 无水 ,需要使FR3, FR2, FR1 都打开(111) S3 S2 S1 FR3 FR2 FR1 000 111 001 011 011 001 111 000 fr代表水变深为…...
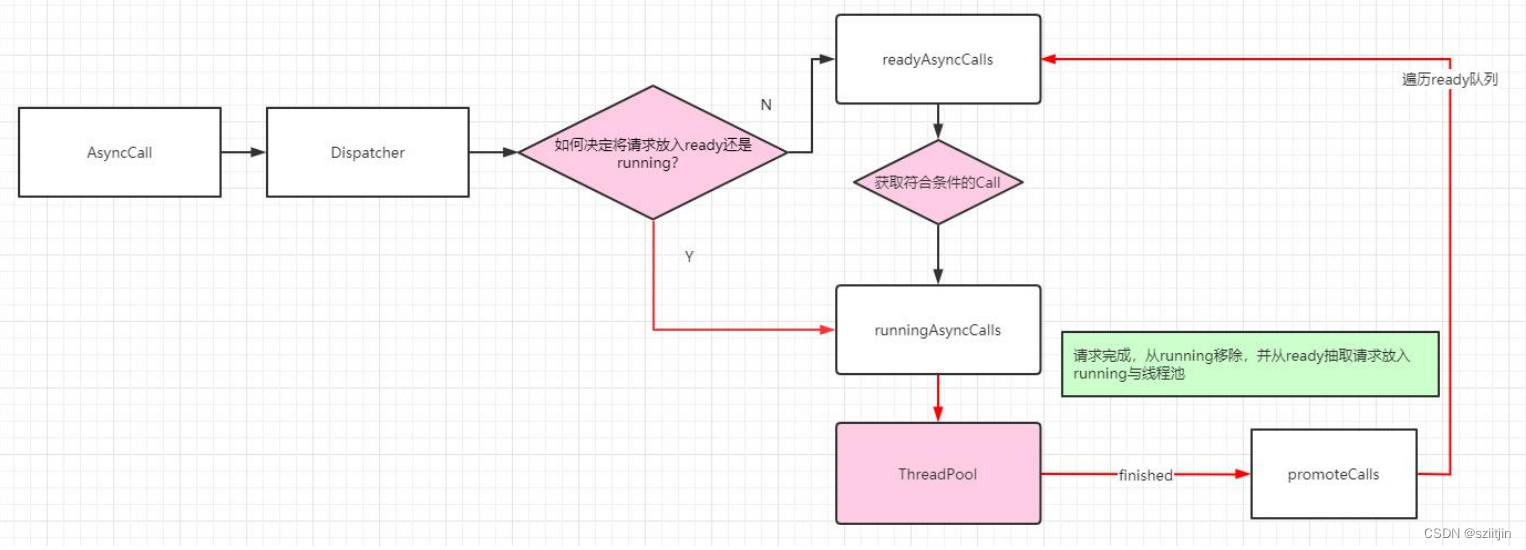
Android OkHttp源码分析--分发器
OkHttp是当下Android使用最频繁的网络请求框架,由Square公司开源。Google在Android4.4以后开始将源码中 的HttpURLConnection底层实现替换为OKHttp,同时现在流行的Retrofit框架底层同样是使用OKHttp的。 OKHttp优点: 1、支持Http1、Http2、Quic以及Web…...
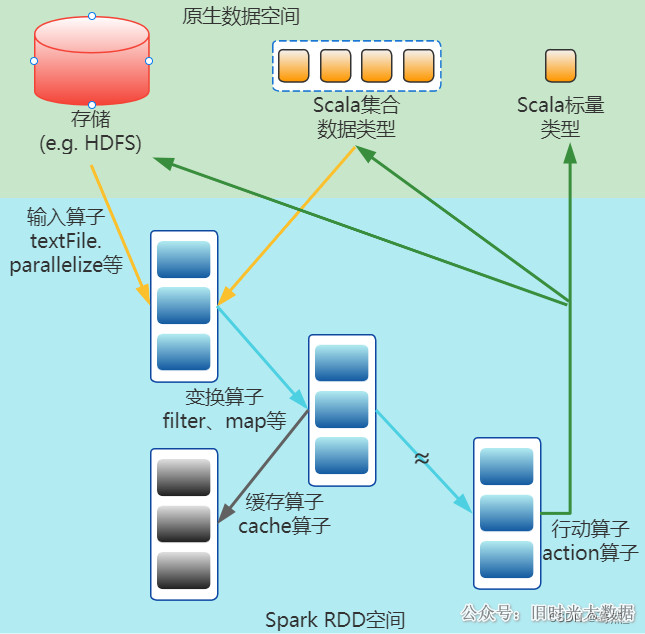
大数据面试题:说下Spark中的Transform和Action,为什么Spark要把操作分为Transform和Action?
面试题来源: 《大数据面试题 V4.0》 大数据面试题V3.0,523道题,679页,46w字 可回答:Spark常见的算子介绍一下 参考答案: 我们先来看下Spark算子的作用: 下图描述了Spark在运行转换中通过算…...
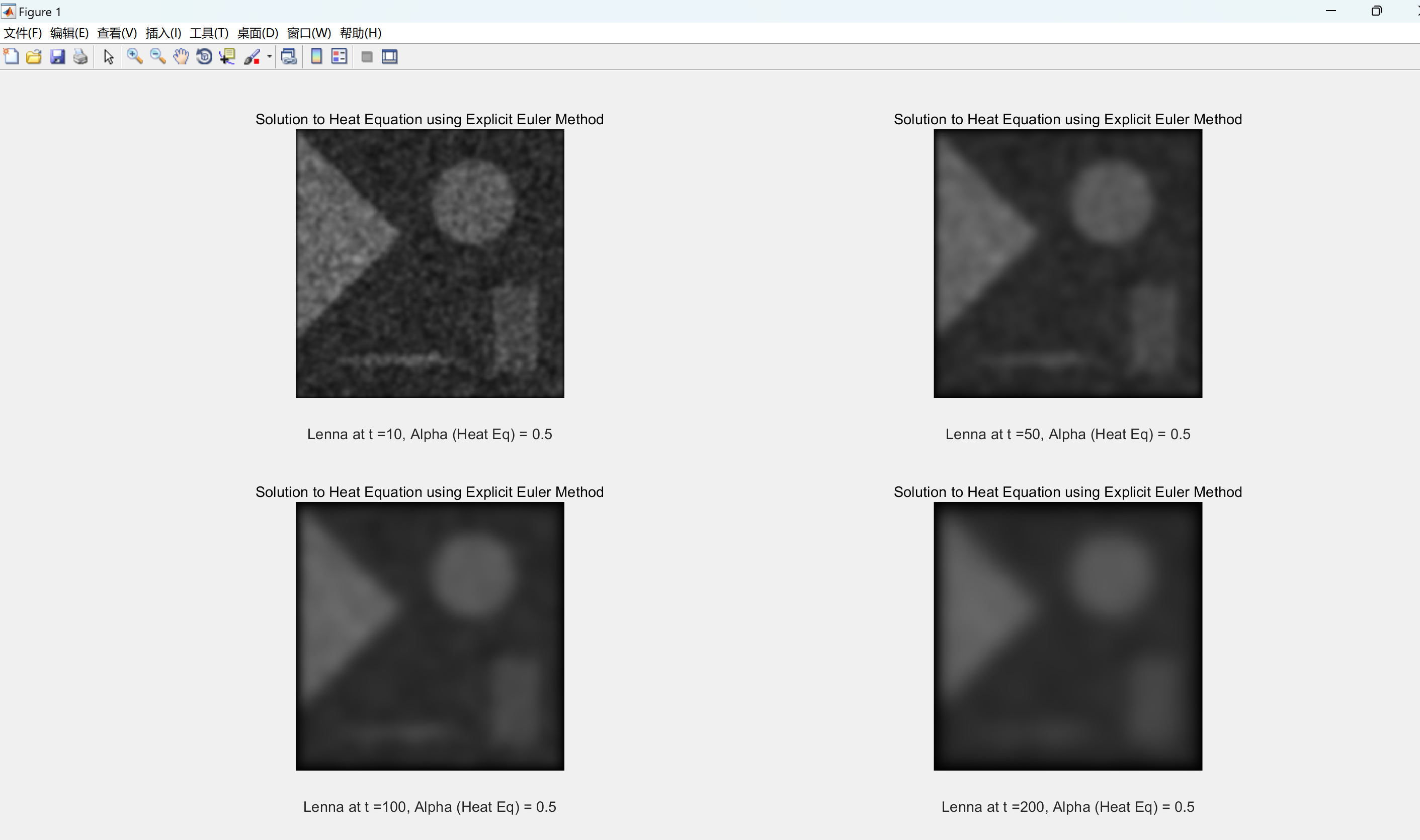
【图像去噪的扩散滤波】基于线性扩散滤波、边缘增强线性和非线性各向异性滤波的图像去噪研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
)
python函数、运算符等简单介绍2(无顺序)
list(列表) 列表是Python的一种内置数据类型,列表是可以装各种数据类 型的容器 # 第一种list创建方式 list_name [晓东,小刚,明明,小红,123,123.4,123] print(list_name) print(type(list_name)) # 输出结果: [晓东, 小刚, 明明…...

k8s 自身原理 3
前面有分享到 master 主节点上的 四个组件,etcd,ApiServer,scheduler,controller manager 接下来我们分享一波 woker 节点上的组件,xdm 还记得 worker 节点上都有什么吗? kubeletkube-proxy实际的服务对应…...
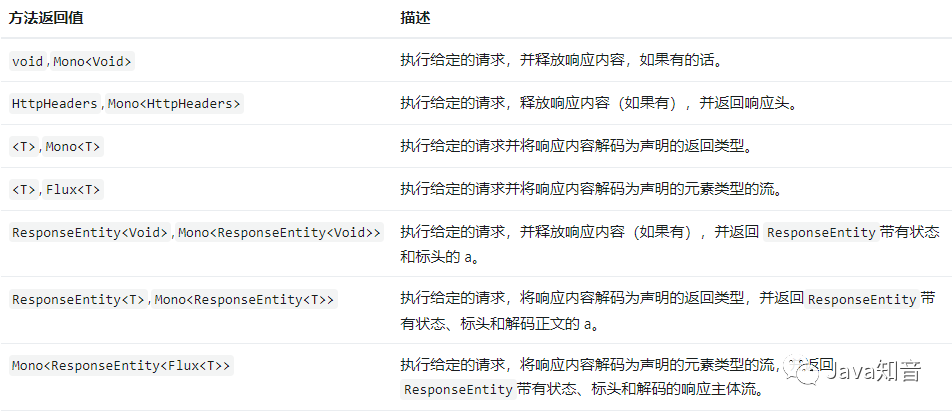
SpringBoot 3自带的 HTTP 客户端工具
原理 Spring的HTTP 服务接口是一个带有HttpExchange方法的 Java 接口,它支持的支持的注解类型有: HttpExchange:是用于指定 HTTP 端点的通用注释。在接口级别使用时,它适用于所有方法。GetExchange:为 HTTP GET请求指…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...
