数据分析 | 为什么Bagging算法的效果优于单个评估器
1. 回归问题如何降低方差
以随机森林为例,假设随机森林中含有n个弱评估器,由于子样本集的相似性以及使用的是同种模型,因此各模型有近似相等的方差和偏差,因此假设任意弱评估器上输出结果为,方差均为
,则随机森林的输出结果为
,当各棵树相互独立时有如下关系:

由上述公式可知,随机森林在经过Bagging之后的方差一定小于单个评估器的方差,这也是随机森林的泛化能力总是强于单一决策树的根本原因。其中泛化误差为模型在测试集上的误差,有如下关系:
![]()
2. 分类问题如何降低方差
Bagging在执行分类任务时总是遵循少数服从多数的原则,同样可以通过回归器进行预测,只是在回归的基础上套上sigmoid函数,以0.5为阈值进行划分,即能将回归转化为分类。其中,sigmoid函数如下:

由于sigmoid函数是二阶可导函数,根据泰勒展开以及方差的运算性质有如下关系:

一阶导后平方的sigmoid函数值域为[0,0.0625],因此在分类问题上Bagging算法也是能降低方差的。
3. Bagging有效的条件
由于Bagging不能降低偏差,因此要求弱评估器的偏差较低,准确率至少在50%以上;由于方差降低的必要条件是各个弱评估器之间相互独立,因此要求弱评估器之间的相关性尽可能弱,可以通过随机采样来降低相关性。其中,ESL(p588)教材有如下公式。由此可知弱评估器的相关性越强,随机森林输出结果的方差就越大。

相关文章:

数据分析 | 为什么Bagging算法的效果优于单个评估器
1. 回归问题如何降低方差 以随机森林为例,假设随机森林中含有n个弱评估器,由于子样本集的相似性以及使用的是同种模型,因此各模型有近似相等的方差和偏差,因此假设任意弱评估器上输出结果为,方差均为,则随机森林的输出…...
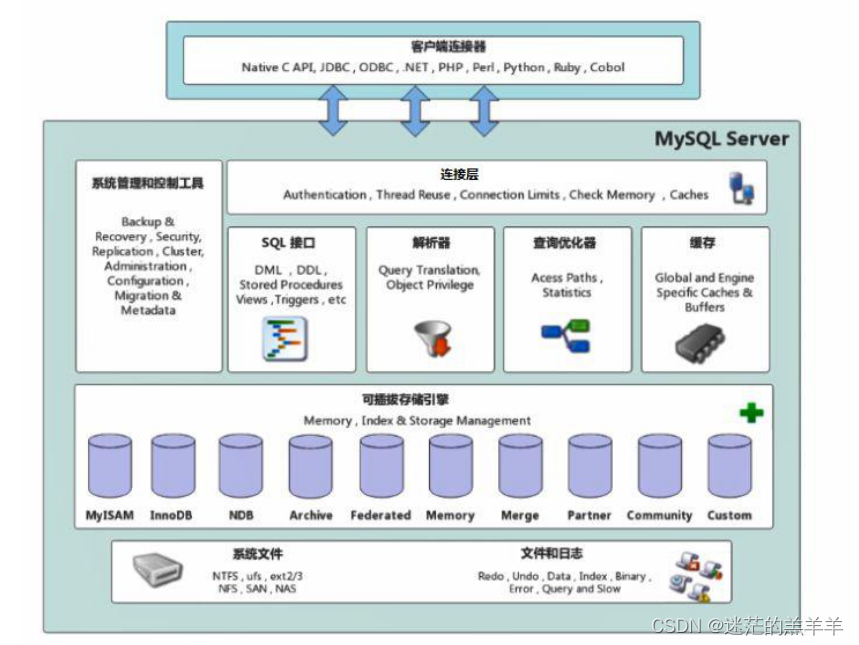
mysql架构介绍
1.整体架构图 我们发现整体的体系是由连接层、服务层、引擎层和物理文件存储层组成。 1.连接层 连接层是处理客户端和服务端之间的通信的,比如一些连接处理、授权验证等等。 2.服务层 服务层主要完成核心的功能,如SQL接口,就是用来接收…...
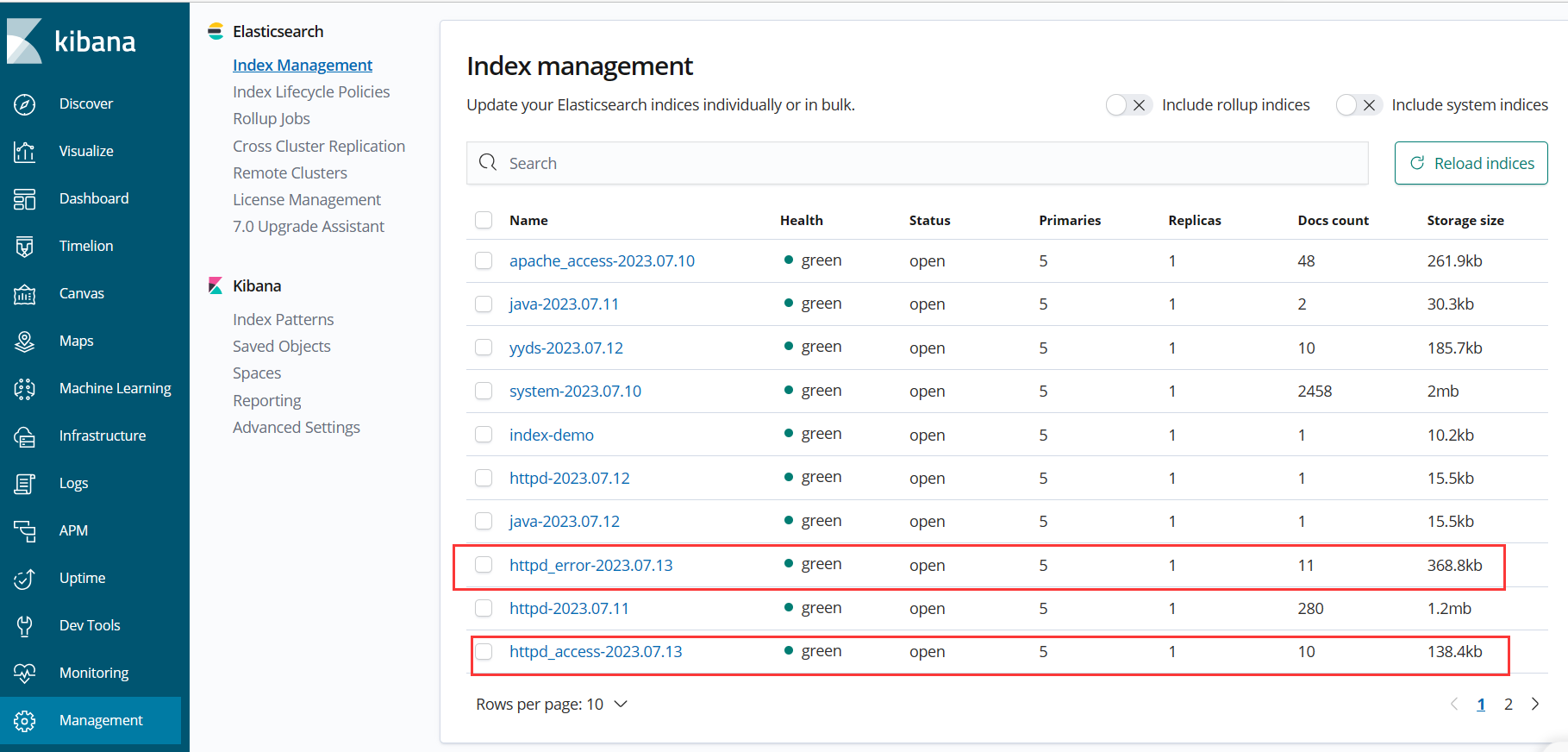
EIK+Filebeat+Kafka
目录 一、Kafka 概述 1)为什么需要消息队列(MQ) 2)使用消息队列的好处 (1)解耦 (2)可恢复性 (3)缓冲 (4)灵活性 & 峰值处理…...

python安装xgboost报错
ERROR: Could not find a version that satisfies the requirement xgboost (from versions: none) ERROR: No matching distribution found for xgboost 解决办法: 换成国内的pip源 pip install xgboost -i http://pypi.doubanio.com/simple/ --trusted-host py …...
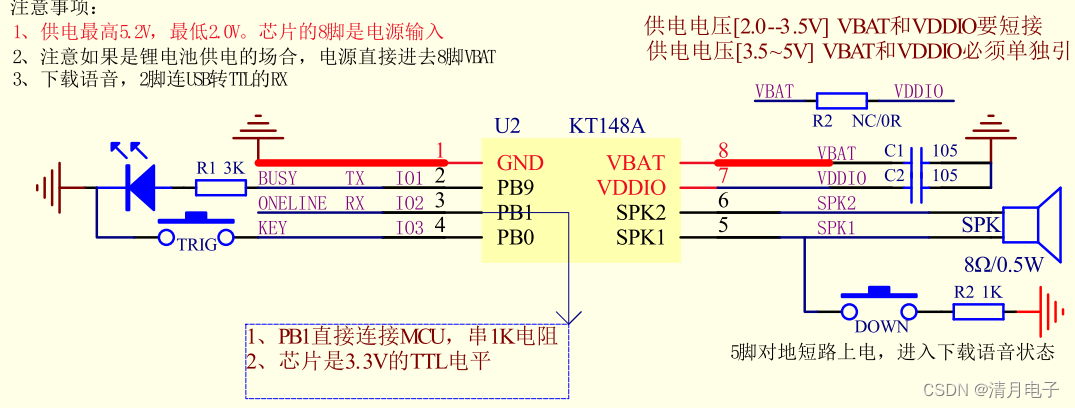
语音芯片的型号有哪些?为什么强烈推荐使用flash型可擦写的
一、语音芯片的简介 语音芯片的型号有哪些?为什么强烈推荐使用flash型可擦写的芯片。这里我们简单描述一下如下常见类容: 1、他们都有什么特点?以及发展的历程简介 2、常见的语音芯片有哪些? 3、为什么推荐使用flash型可以重复…...

【OpenCV常用函数:轮廓检测+外接矩形检测】cv2.findContours()+cv2.boundingRect()
文章目录 1、cv2.findContours()2、cv2.boundingRect() 1、cv2.findContours() 对具有黑色背景的二值图像寻找白色区域的轮廓,因此一般都会先经过cvtColor()灰度化和threshold()二值化后的图像作为输入。 cv2.findContous(image, mode, method[, contours[, hiera…...

opencv,opengl,osg,vulkan,webgL,opencL,cuda
OpenCV OpenCV是一个基于BSD许可(开源)发行的跨平台计算机视觉和机器学习软件库,可以运行在Linux、Windows、Android和Mac OS操作系统上。 它轻量级而且高效——由一系列 C 函数和少量 C 类构成,同时提供了Python、Ruby、MATLAB等…...
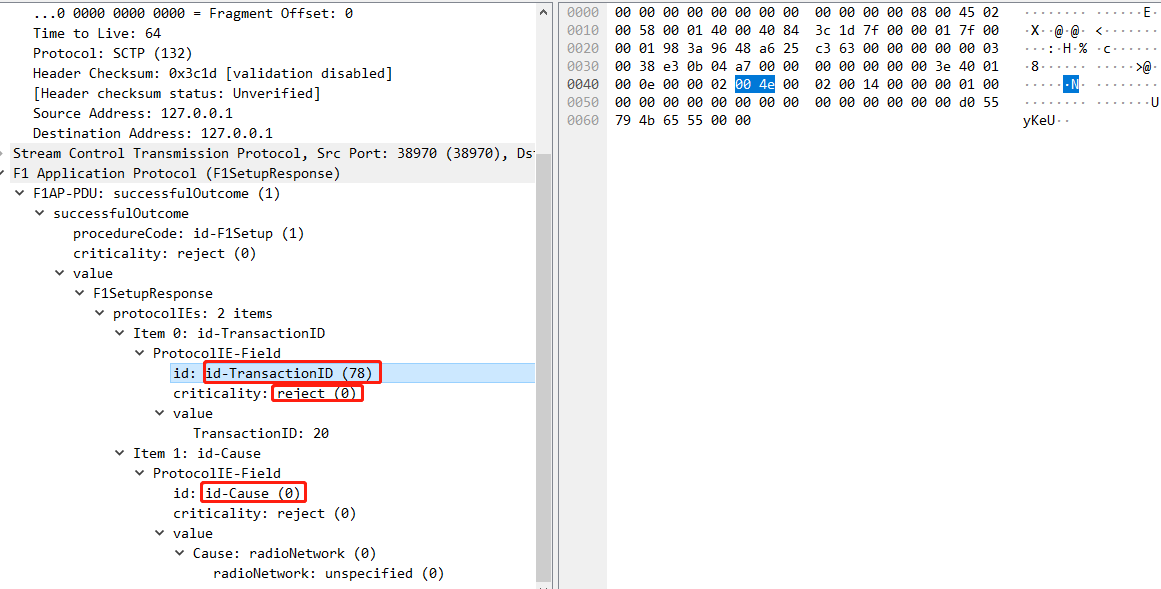
golang拥有wireshark数据包解析能力
golang拥有wireshark数据包解析能力 1. 功能和实现 wireshark拥有世界上最全面的协议解析能力并且还在不断更新中,通过调研,没有办法找到与wireshark同水平的解析工具。 为了使得golang语言可以拥有wireshark一样强大的协议解析能力,库 gowir…...

Redis_分片集群
10. 分片集群 10.1简介 业务场景,需要存储50G的数据。对于内存和硬盘配置不足,选用两种方式 一种:纵向扩展:加内存,加硬盘,提高CPU。简单、直接。RDB存储效率要考虑。成本要考虑。二种:横向扩…...

测试提升方向:你选测试开发?还是性能测试?
如果想要在测试领域好好发展,提升自己的测试技术是必不可少的,但是,选对方向更为重要,功能测试、自动化测试、测试开发、性能测试、安全测试、测试管理,每个测试方向都不简单,但是,大环境就是&a…...

无涯教程-Perl - print函数
描述 此函数将LIST中的表达式的值打印到当前的默认输出文件句柄或FILEHANDLE指定的句柄中。 如果设置,则$\变量将添加到LIST的末尾。 如果LIST为空,则打印$_中的值。 print接受一个值列表,列表中的每个元素都将被解释为一个表达式。 语法 以下是此函数的简单语法- print…...

python搜索文件夹内类似的文件名
# codingutf8 __author__ Administrator import os """ #编写函数,计算字符串匹配的准确率 def Rate(origin,userInput): if not (isinstance(origin,str) and isinstance(userInput,str)): print(The two parameters must be strings…...
[保研/考研机试] KY3 约数的个数 清华大学复试上机题 C++实现
题目链接: KY3 约数的个数 https://www.nowcoder.com/share/jump/437195121691716950188 描述 输入n个整数,依次输出每个数的约数的个数 输入描述: 输入的第一行为N,即数组的个数(N<1000) 接下来的1行包括N个整数,其中每个…...
——windows下动态设置输出文件(dll/exe)版本)
cmake扩展(2)——windows下动态设置输出文件(dll/exe)版本
准备 windows下设置文件的版本需要通过VERSIONINFO接口,详情参考VERSIONINFO resource。这里我们根据模板做了一定的修改。 1 VERSIONINFOFILEVERSION ${GIT_VERSION} //文件版本号,必填。以,分隔,输出以.分隔。这里是取CMakeLists里的GIT_…...
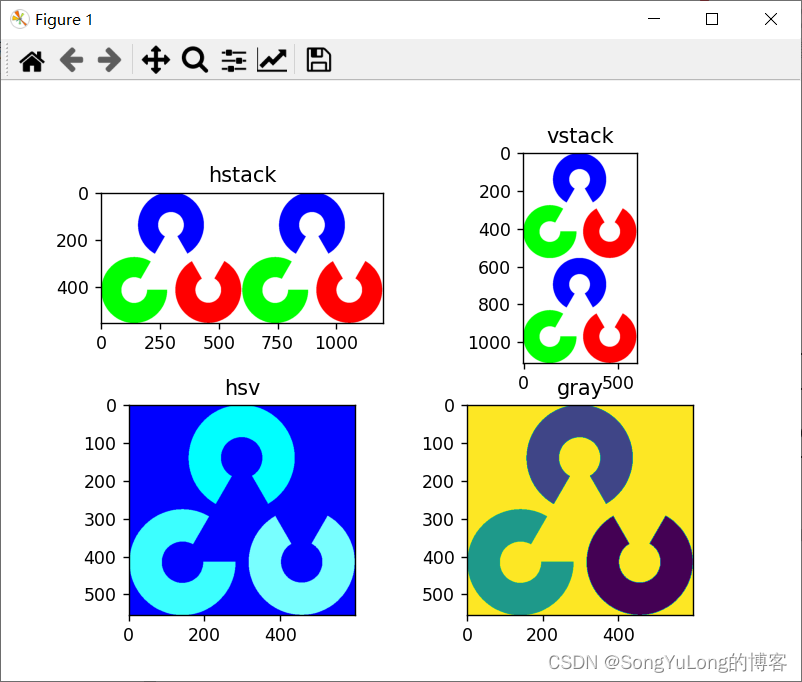
Python-OpenCV中的图像处理-颜色空间转换
Python-OpenCV中的图像处理-颜色空间转换 颜色空间转换获取HSV的值 颜色空间转换 在 OpenCV 中有超过 150 中进行颜色空间转换的方法。但是你以后就会 发现我们经常用到的也就两种: BGR G r a y 和 B G R Gray 和 BGR Gray和BGRHSV。 注意:在 OpenCV 的…...

yolov5目标检测多线程Qt界面
上一篇文章:yolov5目标检测多线程C部署 V1 基本功能实现 mainwindow.h #pragma once#include <iostream>#include <QMainWindow> #include <QFileDialog> #include <QThread>#include <opencv2/opencv.hpp>#include "yolov5.…...
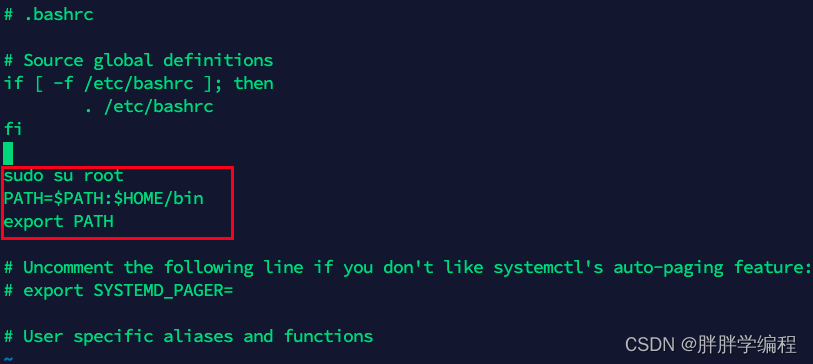
[ubuntu]创建root权限的用户 该用户登录后自动切换为root用户
一、创建新用户 1、创建新用户 sudo useradd -r -m -s /bin/bash 用户名 # -r:建立系统账号 -m:自动建立用户的登入目录 -s:指定用户登入后所使用的shell2、手动为用户设置密码 passwd 用户名 二、为用户增加root权限 1、添加写权限 ch…...

大连交通大学813软件工程考研习题
1.什么是软件生存周期模型?有哪些主要模型? 生存周期模型:描述软件开发过程中各种活动如何执行的模型。对软件开发提供强有力的支持,为开发过程中的活动提供统一的政策保证,为参与开发的人员提供帮助和指导,是软件生存周期模型…...
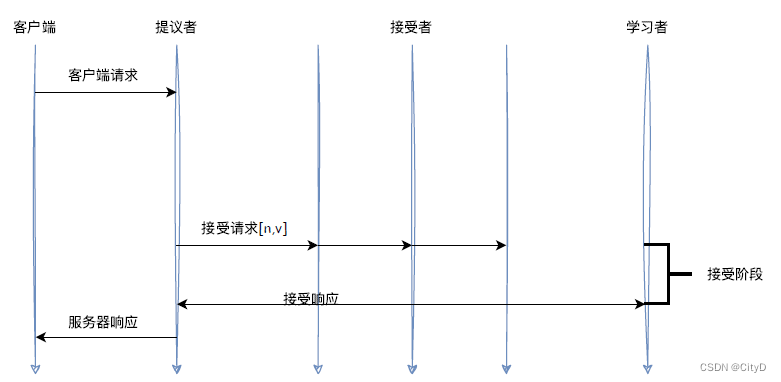
分布式协议与算法——Paxos算法
目录 Paxos算法Basic Paxos算法三种角色如何达成共识(协商过程)小结: Multi-Paxos算法关于 Multi-Paxos 的思考领导者优化Basic PaxosChubby 的 Multi-Paxos 实现小结 参考 Paxos算法 Paxos论文 Paxos Made Simple 、author:Lesli…...

Spring中的Websocket身份验证和授权
目录 一、需要了解的事项二、依赖三、WebSocket 配置3.1 、简单的消息代理3.2 、Spring安全配置 一、需要了解的事项 http和WebSocket的安全链和安全配置是完全独立的。SpringAuthenticationProvider根本不参与 Websocket 身份验证。将要给出的示例中,身份验证不会…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...
