P4178 Tree (点分治)
题目链接
一:我们考虑树上两点之间的路径有什么情况
1:经过根节点(即在根节点的两端)
2:不经过根节点(完全在一颗子树的一侧)
二:我们考虑这两种路径是否可以归为一类
1:对于第一种的情况两点间路径长度dis( u , v ) 可以看为dis ( u , root ) + dis ( root , v )
2:而对于第二种情况我们可以找到u , v 路径所在的子树,将根节点变为子树的根节点,然后就变为了第一种情况
3:总之,所以我们可以不断的递归根节点将所有情况转化为第一种情况
设b[ u ] 表示u属于哪一棵子树(b数组在算法进阶指南里说了,但是代码好像没有体现,而是用了容斥原理)
那么b[ u ] = b[ v ] ,d[ u ] + d[ v ] ≤ k满足条件的第一类路径条数即为满足条件的点对数
三:下面我们来讨论如何计算满足条件的点对数:
1:将目前子树中的节点到根节点的权值放入数组len中,并排序
用两个指针 L,R 扫描数组,每找到一个合法的答案就加上R −L ,就让L++,否则让 R --
2:发现问题
在指针扫描的过程中我们会出现不合的情况
根据len的定义我们存放的一颗树里面所有的边,这是我们计算calc计算时,可能会加上两条边在子树的同一侧的情况,我们可以发现不合法的路径在当前根的一颗子树上,即没有跨越两棵子树(如果跨越了它就合法了),所以们可以在遍历的时候减去不合法的情况(容斥)
3:具体的方法
ans+ = calc( u , 0 )
ans − =calc ( v , dis ( u , v ) )
这样即可做到不重不漏
四:总结
点分治步骤
- 找到树的重心
- 将重心视为根节点,那么树上任意两点有两种情况
- 路径经过根节点
- 路径不经过根节点
- 通过 calc 函数计算出第一种情况下的答案,把根节点从树中删去
- 对每棵子树递归执行上面的操作
calc函数的计算方法
- 计算出每个结点到根节点的距离 d [ i ]
- 将树上的结点按照 d [ i ] 递增排序
- 指针 l 指向 d [ 1 ] ,指针 r 指向 d [ n ]。
- 若 l 与 r 指向结点的距离小于 k ,则 ans + = r − l + 1 , l + + 。
- 否则 r − −。
- 当 l > = r 的时候退出循环。
- 按照上面的方法,会把不经过根节点的路径也算入进去。利用容斥原理修正答案:
五:更具体的做法,见注释
#include <bits/stdc++.h>
using namespace std;
#define pi acos(-1)
#define xx first
#define yy second
#define endl "\n"
#define lowbit(x) x & (-x)
#define int long long
#define ull unsigned long long
#define pb push_back
typedef pair<int, int> PII;
typedef pair<double, double> PDD;
#define max(a, b) (((a) > (b)) ? (a) : (b))
#define min(a, b) (((a) < (b)) ? (a) : (b))
#define Ysanqian ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
const int N = 1e6 + 10, M = 1010, inf = 0x3f3f3f3f, mod = 18446, P = 13331;
const double eps = 1e-8;
int n, k, root, sum, ans;
vector<PII> g[N];
int siz[N], max_part[N], d[N], b[N], len[N];
bool st[N];
void get_root(int u, int fa) // 找出重心
{siz[u] = 1, max_part[u] = 0; // siz[i]为其子树的大小,max_part[i]为去掉i后的最大连通块大小for (auto ed : g[u]){int v = ed.xx;if (v == fa || st[v])continue;get_root(v, u);siz[u] += siz[v];max_part[u] = max(max_part[u], siz[v]);}max_part[u] = max(max_part[u], sum - siz[u]);if (max_part[u] < max_part[root]) // 一开始root为0,且将其赋值为 n即为maxroot = u;
}
void get_dis(int u, int fa) // 找出这颗子树的距离。
{len[++len[0]] = d[u]; // len[0]存放的是子树节点个数,len[i] 表示子树中的路径长度for (auto ed : g[u]){int v = ed.xx, w = ed.yy;if (v == fa || st[v])continue;d[v] = d[u] + w; // d[i] 表示i到根节点的距离,由上而下的去跟新d数组,因为子节点距离有父节点跟新而来,故在计算距离时只更新父节点即可get_dis(v, u);}
}
int calc(int u, int w) // 计算以u为根的第一种情况的答案,也就是在树的两边的,但是对于只在一边得还未计算
{d[u] = w, len[0] = 0; // 先给根节点一个值,如果为0说明在递归子树,不是0那就是再利用容斥出去冗余,将该子树的边数先归零get_dis(u, 0); // 计算改子树的距离根节点的距离sort(len + 1, len + len[0] + 1); // 将距离从小到大排序int res = 0;for (int l = 1, r = len[0]; l < r;) // 直到不论左移还是右移都大于k,if和else if 都进不去{if (len[l] + len[r] <= k) // l与最大的相加都小于k,其余也小于k{res += r - l; // 故加上r-l++l; // 右移左端点}elser--; // 否则左移右端点}return res; // 返回以u为根的所有情况的答案
}
void solve(int u)
{st[u] = 1; // 标记删除的重心,防止重复计算ans += calc(u, 0); // 加上以我为跟答案for (auto ed : g[u]) // 遍历子树{int v = ed.xx, w = ed.yy;if (st[v])continue;ans -= calc(v, w); // 减去不合法得情况,不合法的情况全都发生在一课子树上,这里为什么传w,因为我们要加上u与v的边权sum = siz[v]; // 不要忘记在以v为根节点时,要修改all_node 的大小root = 0;get_root(v, u); // 递归根节点,但是肯定会有重复solve(root); // 递归解决}
}
signed main()
{Ysanqian;cin >> n;sum = n;max_part[0] = n; // 让max_part[0]为n当一个哨兵,以便跟新max_part[i]for (int i = 1; i < n; i++){int a, b, c;cin >> a >> b >> c;g[a].pb({b, c}); // 建边g[b].pb({a, c});}cin >> k;get_root(1, -1); // 先找重心solve(root); //cout << ans << endl;return 0;
}相关文章:
)
P4178 Tree (点分治)
题目链接 一:我们考虑树上两点之间的路径有什么情况 1:经过根节点(即在根节点的两端) 2:不经过根节点(完全在一颗子树的一侧) 二:我们考虑这两种路径是否可以归为一类 1࿱…...

Kubernetes 二进制搭建
Kubernetes 二进制搭建 一、二进制搭建 Kubernetes v1.201.1 部署准备1.2 操作系统初始化配置1.3 部署 etcd 集群1.3.1 etcd 作为服务发现系统,有以下的特点1.3.2 准备签发证书环境1.3.3 在 master01 节点上操作1.3.4 生成证书 1.4 部署 docker引擎1.4.1 部署 Maste…...
QT QtXlsx安装使用
QtXlsx介绍 QtXlsx是一个可以读取和写入Excel文件的库。它不需要Microsoft Excel,可以在Qt5支持的任何平台上使用。 这里一定是需要QT5支持的。 须知安装QtXlsx时,需要下载perl 1.安装perl 这里选择官网下载安装即可。 官网地址:https://p…...
Java医院信息化HIS管理系统源码
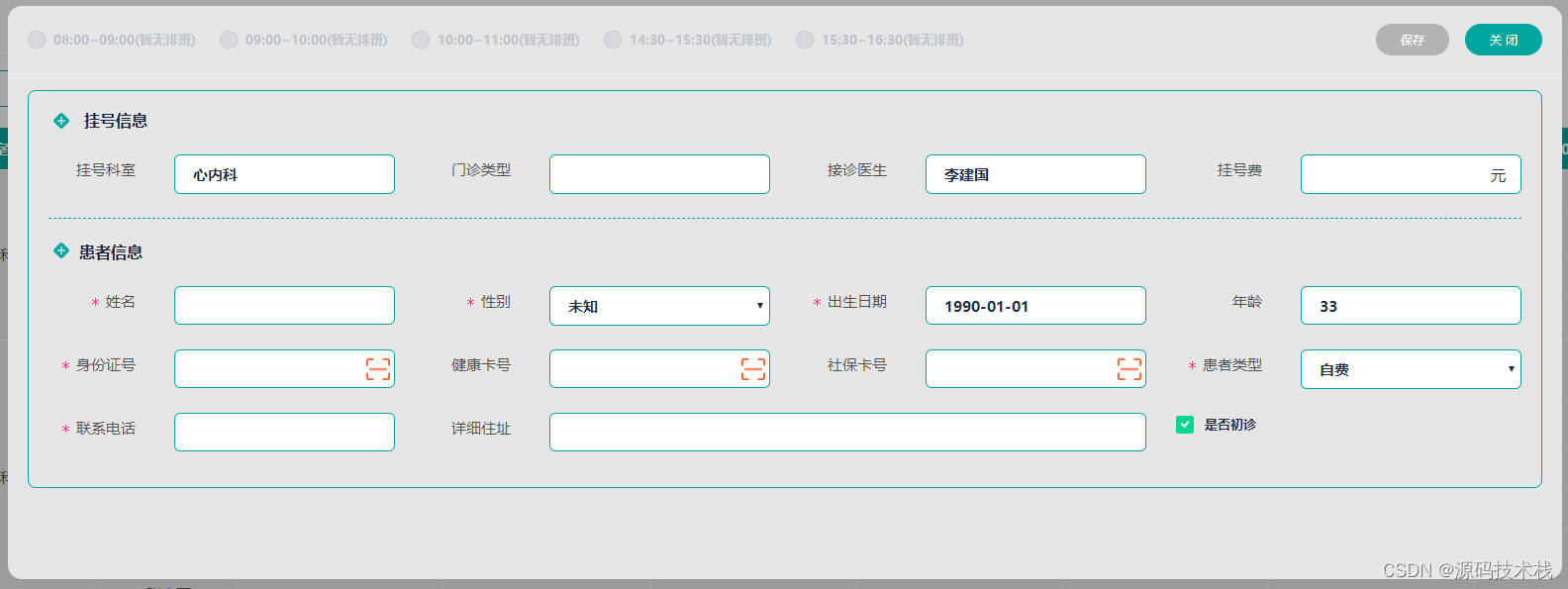
HIS模板分为两种:病历模板和报表模板。模板管理是运营管理的核心组成部分,是基层卫生健康云中各医疗机构定制电子病历和报表的地方,各医疗机构可根据自身特点特色定制电子病历和报表,制作的电子病历及报表可直接在业务系统中使用。…...

【Uni-App】uview 开发多端应用,密码显示隐藏功能不生效问题
出现的问题: 使用uview组件u-input框密码绑定时会出现右侧密码显隐图标不显示的问题 思路: 1.看了下uview源码,发现这有一段注释,我们需要把源码修改一下,问题出在这里 这行代码修改为 :password"password || …...

人工智能算法-SVM, KNN
目录 SVM, KNN区别 一、KNN算法概述 算法的描述: 二、关于K的取值 K的取法: 三、关于距离的选取 Euclidean Distance 定义: 四、总结 SVM, KNN区别...

计算机网络—TCP
这里写目录标题 TCP头格式有哪些为什么需要TCP,TCP工作在哪什么是TCP什么是TCP连接如何确定一个TCP连接TCP和UDP的区别,以及场景TCP和UDP能共用一个端口?TCP的建立TCP三次握手过程为什么是三次握手、不是两次、四次why每次建立连接࿰…...

Oracle到DM实时数据同步实施方案
目录 1 项目概述 2 需求分析 3 实施操作 3.1 历史数据全量同步 3.2 增量数据实时同步 4 问题总结 4.1 字符型非空约束 4.2 字符型唯一索引尾部空格 1 项目概述 将Oracle 11g RAC生产环境数据同步到DM8分析环境,Oracle数据库大小1.5T,日增归档10…...

WebRTC | 音视频实时通信的本质
目录 一、音视频实时通信的两种指标 1. 实时通信延迟指标 2. 视频相关的基本概念 3. 音视频服务质量指标 二、解决实时通信的主要矛盾 1. 增加带宽 A. 提供更优质的接入服务 B. 保证云端网络的带宽和质量 C. 更合理的路由调度策略 2. 减少数据量 A. 采用更好的压缩算…...
ApiPost的使用
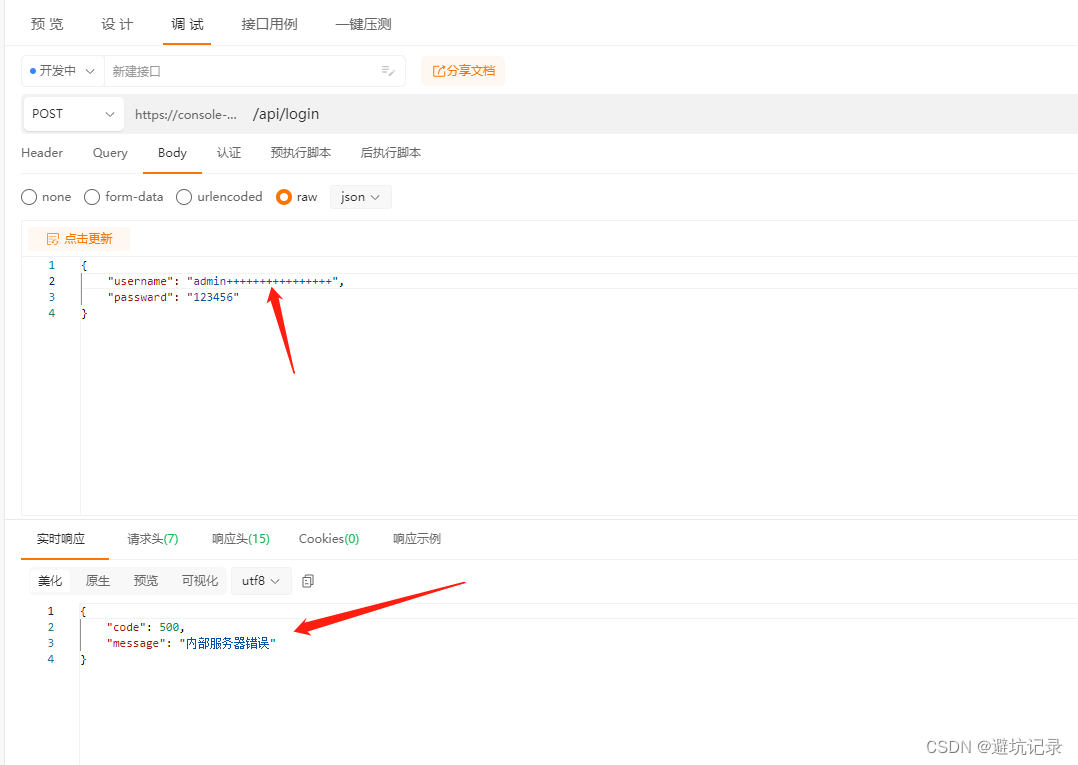
1. 设计接口 请求参数的介绍 Query:相当于get请求,写的参数在地址栏中可以看到 Body: 相当于 post请求,请求参数不在地址栏中显示。 请求表单类型,用form-data json文件类型,用row 2. 预期响应期望 设置完每一项点一下生成响应…...

6、CCS 配置工程头文件批量添加路径的方法
1、进入到图示的框框里 2、编辑好需要添加的路径,并按ctrl c 3、选中include paths(-I)框框里的最后一条路径 4、然后ctrl v,这样路径就复制到预定义路径里了...
Visual Studio配置PCL库
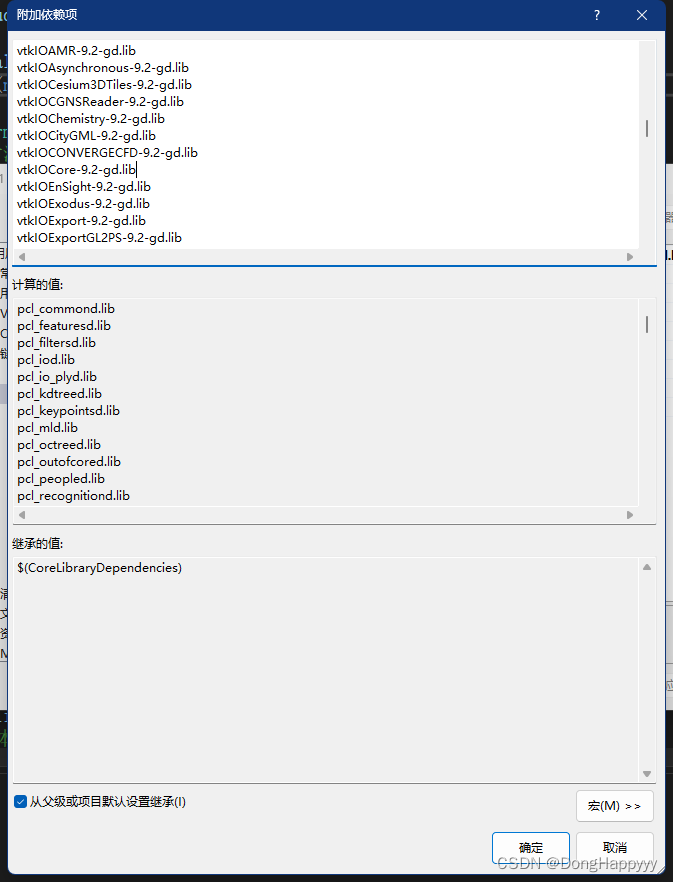
Visual Studio配置PCL库 Debug和Release配置新建项目配置属性表测试参考 Debug和Release Debug和Release的配置过程一模一样,唯一区别就在于最后一步插入的附加依赖项不同,因此下面以debug为例。 配置新建项目 1、新建一个C空项目,模式设置…...

数据分析 | 为什么Bagging算法的效果优于单个评估器
1. 回归问题如何降低方差 以随机森林为例,假设随机森林中含有n个弱评估器,由于子样本集的相似性以及使用的是同种模型,因此各模型有近似相等的方差和偏差,因此假设任意弱评估器上输出结果为,方差均为,则随机森林的输出…...
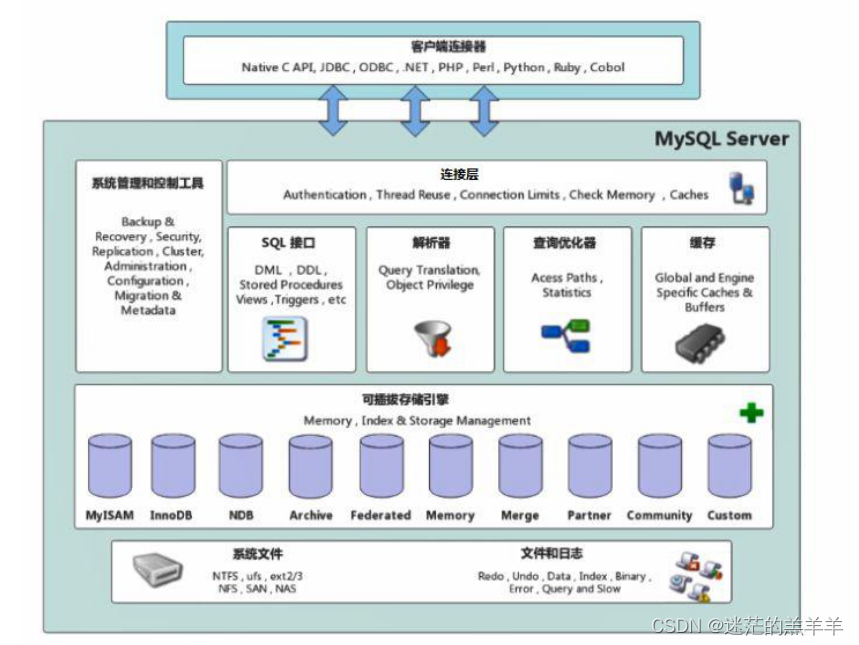
mysql架构介绍
1.整体架构图 我们发现整体的体系是由连接层、服务层、引擎层和物理文件存储层组成。 1.连接层 连接层是处理客户端和服务端之间的通信的,比如一些连接处理、授权验证等等。 2.服务层 服务层主要完成核心的功能,如SQL接口,就是用来接收…...
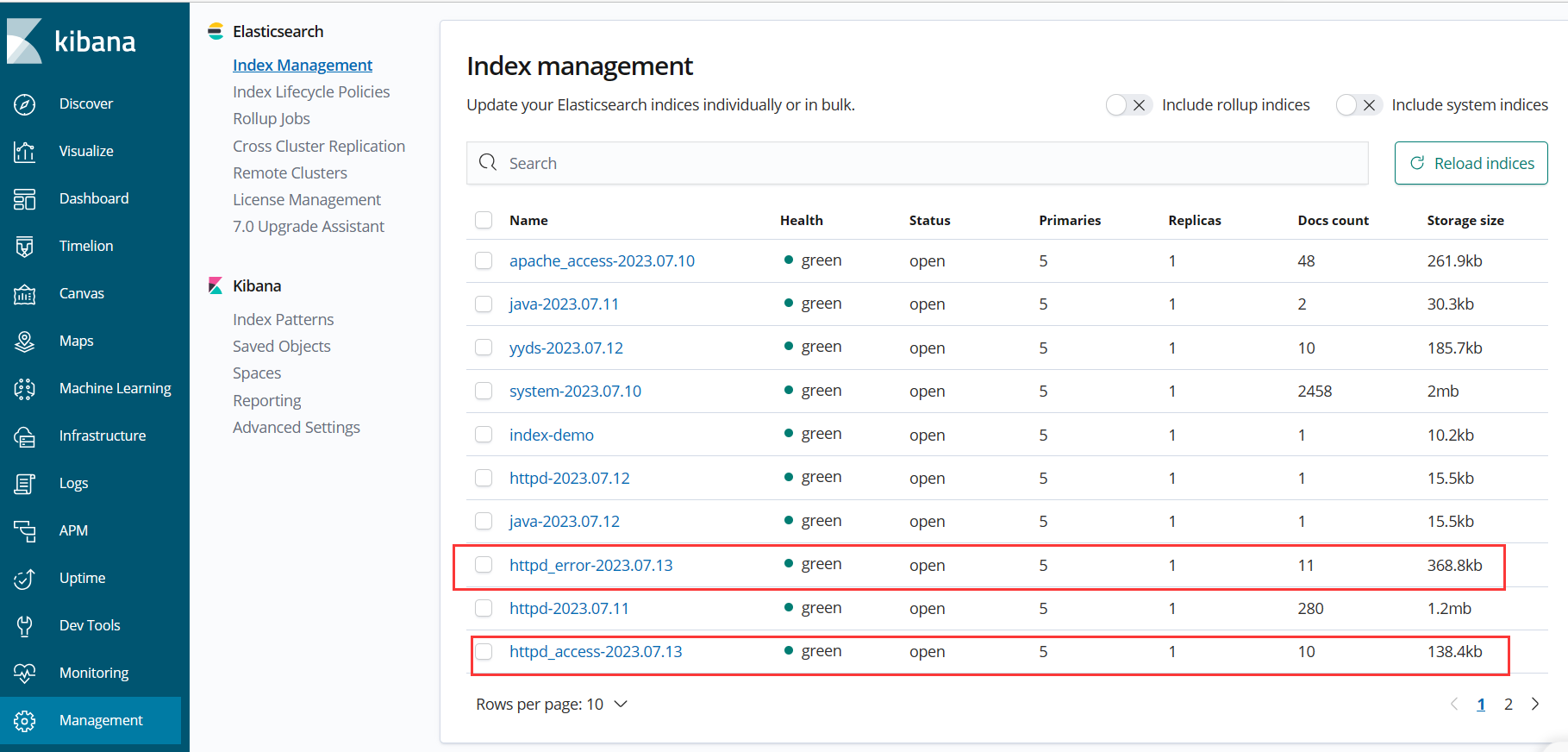
EIK+Filebeat+Kafka
目录 一、Kafka 概述 1)为什么需要消息队列(MQ) 2)使用消息队列的好处 (1)解耦 (2)可恢复性 (3)缓冲 (4)灵活性 & 峰值处理…...

python安装xgboost报错
ERROR: Could not find a version that satisfies the requirement xgboost (from versions: none) ERROR: No matching distribution found for xgboost 解决办法: 换成国内的pip源 pip install xgboost -i http://pypi.doubanio.com/simple/ --trusted-host py …...
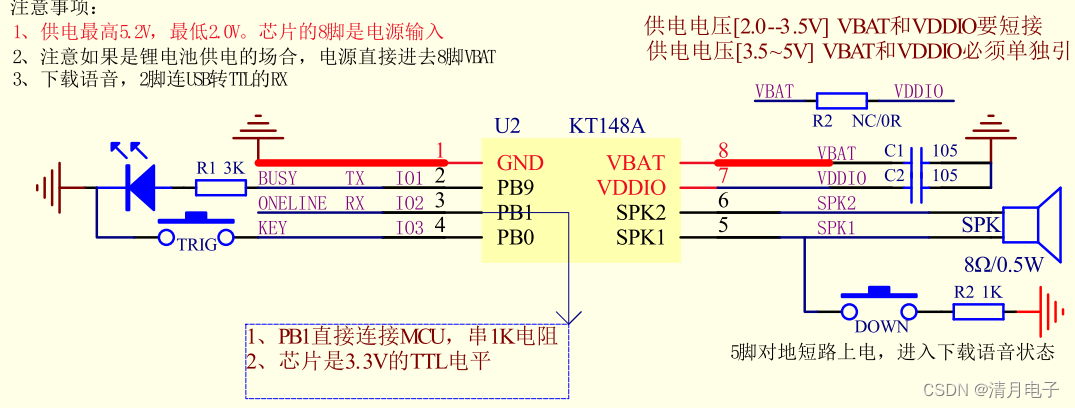
语音芯片的型号有哪些?为什么强烈推荐使用flash型可擦写的
一、语音芯片的简介 语音芯片的型号有哪些?为什么强烈推荐使用flash型可擦写的芯片。这里我们简单描述一下如下常见类容: 1、他们都有什么特点?以及发展的历程简介 2、常见的语音芯片有哪些? 3、为什么推荐使用flash型可以重复…...

【OpenCV常用函数:轮廓检测+外接矩形检测】cv2.findContours()+cv2.boundingRect()
文章目录 1、cv2.findContours()2、cv2.boundingRect() 1、cv2.findContours() 对具有黑色背景的二值图像寻找白色区域的轮廓,因此一般都会先经过cvtColor()灰度化和threshold()二值化后的图像作为输入。 cv2.findContous(image, mode, method[, contours[, hiera…...

opencv,opengl,osg,vulkan,webgL,opencL,cuda
OpenCV OpenCV是一个基于BSD许可(开源)发行的跨平台计算机视觉和机器学习软件库,可以运行在Linux、Windows、Android和Mac OS操作系统上。 它轻量级而且高效——由一系列 C 函数和少量 C 类构成,同时提供了Python、Ruby、MATLAB等…...
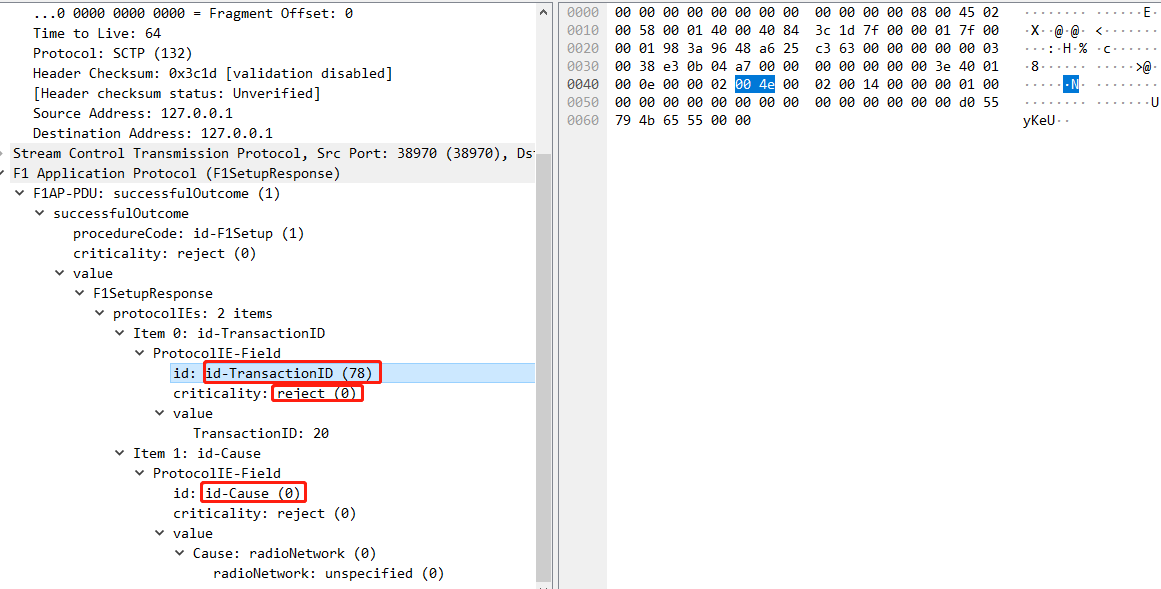
golang拥有wireshark数据包解析能力
golang拥有wireshark数据包解析能力 1. 功能和实现 wireshark拥有世界上最全面的协议解析能力并且还在不断更新中,通过调研,没有办法找到与wireshark同水平的解析工具。 为了使得golang语言可以拥有wireshark一样强大的协议解析能力,库 gowir…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...

第八部分:阶段项目 6:构建 React 前端应用
现在,是时候将你学到的 React 基础知识付诸实践,构建一个简单的前端应用来模拟与后端 API 的交互了。在这个阶段,你可以先使用模拟数据,或者如果你的后端 API(阶段项目 5)已经搭建好,可以直接连…...

macOS 终端智能代理检测
🧠 终端智能代理检测:自动判断是否需要设置代理访问 GitHub 在开发中,使用 GitHub 是非常常见的需求。但有时候我们会发现某些命令失败、插件无法更新,例如: fatal: unable to access https://github.com/ohmyzsh/oh…...

数据结构:泰勒展开式:霍纳法则(Horner‘s Rule)
目录 🔍 若用递归计算每一项,会发生什么? Horners Rule(霍纳法则) 第一步:我们从最原始的泰勒公式出发 第二步:从形式上重新观察展开式 🌟 第三步:引出霍纳法则&…...

SQL注入篇-sqlmap的配置和使用
在之前的皮卡丘靶场第五期SQL注入的内容中我们谈到了sqlmap,但是由于很多朋友看不了解命令行格式,所以是纯手动获取数据库信息的 接下来我们就用sqlmap来进行皮卡丘靶场的sql注入学习,链接:https://wwhc.lanzoue.com/ifJY32ybh6vc…...

生产管理系统开发:专业软件开发公司的实践与思考
生产管理系统开发的关键点 在当前制造业智能化升级的转型背景下,生产管理系统开发正逐步成为企业优化生产流程的重要技术手段。不同行业、不同规模的企业在推进生产管理数字化转型过程中,面临的挑战存在显著差异。本文结合具体实践案例,分析…...
