C#,数值计算——抛物线插值与Brent方法(Parabolic Interpolation and Brent‘s Method)的计算方法与源程序

using System;
namespace Legalsoft.Truffer
{
/// <summary>
/// 抛物线插值与Brent方法
/// Parabolic Interpolation and Brent's Method
/// </summary>
public class Brent : Bracketmethod
{
public double xmin { get; set; }
public double fmin { get; set; }
public double tol { get; set; }
public Brent(double toll = 3.0e-8)
{
this.tol = toll;
}
public double minimize(UniVarRealValueFun func)
{
const int ITMAX = 100;
const double CGOLD = 0.3819660;
double ZEPS = float.Epsilon * 0.001;
double d = 0.0;
double e = 0.0;
double a = (ax < cx ? ax : cx);
double b = (ax > cx ? ax : cx);
double x = bx;
double w = bx;
double v = bx;
double fx = func.funk(x);
double fw = fx;
double fv = fx;
for (int iter = 0; iter < ITMAX; iter++)
{
double xm = 0.5 * (a + b);
double tol1 = tol * Math.Abs(x) + ZEPS;
double tol2 = 2.0 * (tol1);
if (Math.Abs(x - xm) <= (tol2 - 0.5 * (b - a)))
{
fmin = fx;
return xmin = x;
}
if (Math.Abs(e) > tol1)
{
double r = (x - w) * (fx - fv);
double q = (x - v) * (fx - fw);
double p = (x - v) * q - (x - w) * r;
q = 2.0 * (q - r);
if (q > 0.0)
{
p = -p;
}
q = Math.Abs(q);
double etemp = e;
e = d;
if (Math.Abs(p) >= Math.Abs(0.5 * q * etemp) || p <= q * (a - x) || p >= q * (b - x))
{
d = CGOLD * (e = (x >= xm ? a - x : b - x));
}
else
{
d = p / q;
double uu = x + d;
if (uu - a < tol2 || b - uu < tol2)
{
d = Globals.SIGN(tol1, xm - x);
}
}
}
else
{
d = CGOLD * (e = (x >= xm ? a - x : b - x));
}
double u = (Math.Abs(d) >= tol1 ? x + d : x + Globals.SIGN(tol1, d));
double fu = func.funk(u);
if (fu <= fx)
{
if (u >= x)
{
a = x;
}
else
{
b = x;
}
shft3(ref v, ref w, ref x, u);
shft3(ref fv, ref fw, ref fx, fu);
}
else
{
if (u < x)
{
a = u;
}
else
{
b = u;
}
if (fu <= fw || w == x)
{
v = w;
w = u;
fv = fw;
fw = fu;
}
else if (fu <= fv || v == x || v == w)
{
v = u;
fv = fu;
}
}
}
throw new Exception("Too many iterations in brent");
}
}
}
相关文章:

C#,数值计算——抛物线插值与Brent方法(Parabolic Interpolation and Brent‘s Method)的计算方法与源程序
using System; namespace Legalsoft.Truffer { /// <summary> /// 抛物线插值与Brent方法 /// Parabolic Interpolation and Brents Method /// </summary> public class Brent : Bracketmethod { public double xmin { get; set…...
基于Selenium技术方案的爬取界面内容实践
1. 定位页面(多窗口切换) WebDriver提供了处理多个窗口的能力,这是通过使用“WebDriver.switchTo.window()”方法来切换到已知名称的窗口来实现的。如果名称未知,您可以使用“WebDriver.getWindowHandles()”获取已知窗口列表。您…...
)
线程记录(1)
创建线程: 一、1.继承Thread,重写run(),将操作写入其中 2.创建子类对象,start() 二、1.实现runnable接口,实现run() 2.创建子类对象,将子类对象作为参数传递到thread的构造器中,创建出Thread类…...

requests
操作步骤 安装 requests 发送GET请求 发送POST请求 说明: data: 参数接收form表单数据,后台会⾃动附加form表单请求信息头(data数据格式为字典) json:参数接收json数据,后台会⾃动附加json表单请求信息头&…...

Python 监控 Windows 服务
Python 监控 Windows 服务 Python 在 Windows 系统上可以使用 wmi 模块来实现对 Windows 服务的监控。本文将介绍如何使用 Python 监控 Windows 服务,并实现服务状态的查询和服务启停功能。 安装依赖 在使用 wmi 模块之前,需要先安装 wmi包。可以使用…...
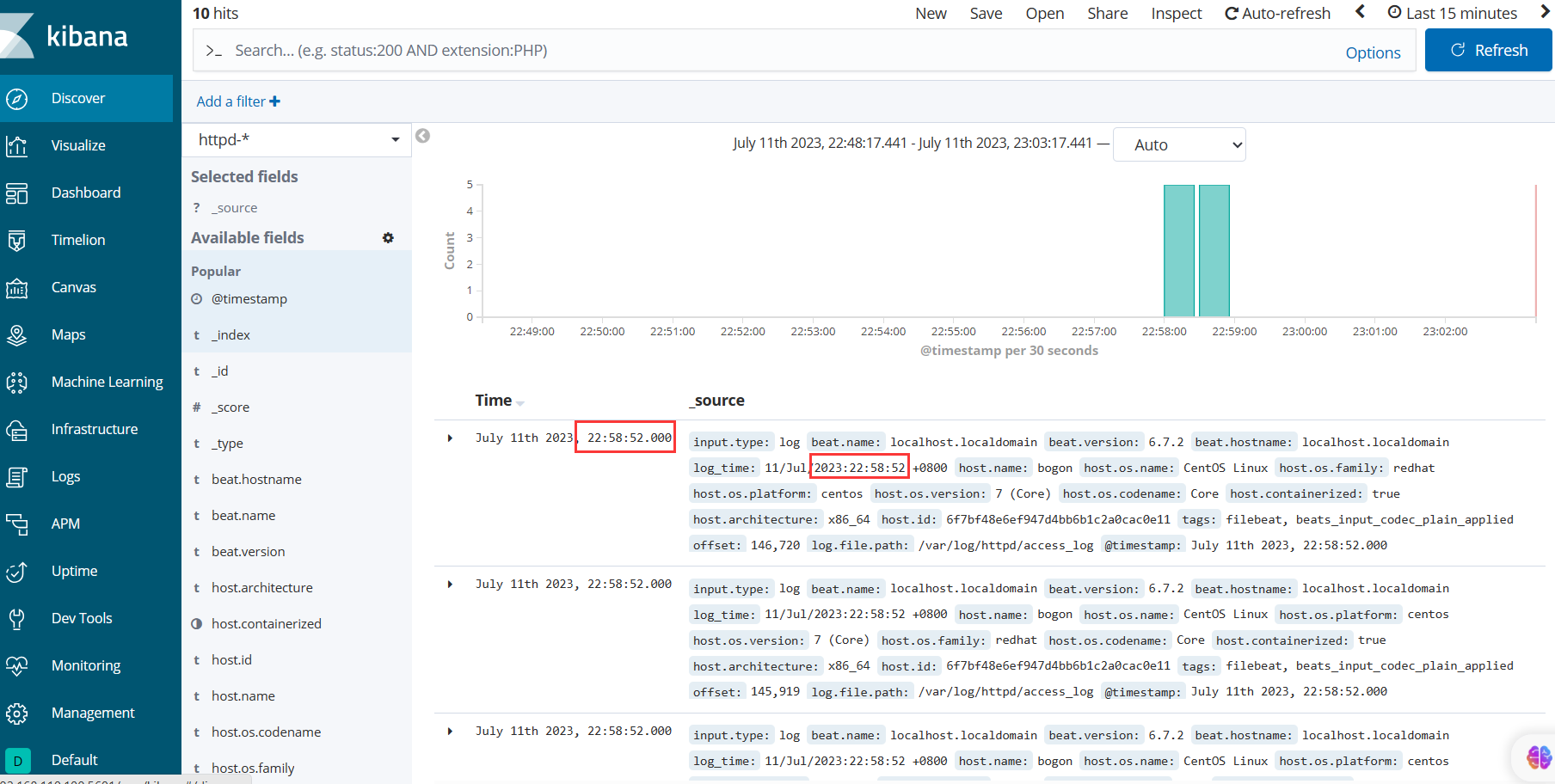
ELK中grok插件、mutate插件、multiline插件、date插件的相关配置
目录 一、grok 正则捕获插件 自定义表达式调用 二、mutate 数据修改插件 示例: ●将字段old_field重命名为new_field ●添加字段 ●将字段删除 ●将filedName1字段数据类型转换成string类型,filedName2字段数据类型转换成float类型 ●将filedNam…...
【C#】静默安装、SQL SERVER静默安装等
可以通过cmd命令行来执行,也可以通过代码来执行,一般都需要管理员权限运行 代码 /// <summary>/// 静默安装/// </summary>/// <param name"fileName">安装文件路径</param>/// <param name"arguments"…...

在vue3中定义组件的5种方式
在vue3中定义组件的5种方式 Vue 正在不断发展,目前在 Vue3 中定义组件的方法有多种。从选项式到组合式再到类API,情况截然不同。本文将会定义一个简单的组件并使用所有可用的方法重构它。 选项式 这是在 Vue 中声明组件的最常见方法。从 Vue1 就开始存…...

算法训练营题目,忘了第几天了
144. 二叉树的前序遍历 给你二叉树的根节点 root ,返回它节点值的 前序 遍历。 输入:root [1,null,2,3] 输出:[1,2,3] var res[]int func preorderTraversal(root *TreeNode) []int {res []int{}traval(root)return res }func traval(no…...

蓝桥杯-统计子矩阵
统计子矩阵 题目链接 思路: 使用前缀和滑动窗口 ,可以先计算出纵向或横向的前缀和,matrix[i][j]表示前i行第j列之和 然后遍历上边界top和下边界buttom,再这个上下边界内使用滑动窗口,由于前面维护了纵向前缀和&…...

在线预览Word、Excel、PowerPoint等文件
在我们工作时,经常会有在线查看各种不同类型的文件的需要,如Word文档、Excel表格、PowerPoint幻灯片和PDF等。可以直接在这里预览:https://www.compdf.com/webviewer/demo Word 文件实现前端预览 方案一: 使用 XDOC 可以实现预…...

准确预测极端降水,哥伦比亚大学推出升级版神经网络 Org-NN
内容一览:随着环境变化加剧,近年来全球极端天气现象频频出现,准确预测降水强度对人类以及自然环境都十分重要。传统模型预测降水的方差较小,偏向小雨,对极端降水预测不足。 关键词:极端天气 内隐学习 神经网…...
【数据结构】反转链表、链表的中间节点、链表的回文结构(单链表OJ题)
正如标题所说,本文会图文详细解析三道单链表OJ题,分别为: 反转链表 (简单) 链表的中间节点 (简单) 链表的回文结构 (较难) 把他们放在一起讲的原因是: 反转链…...

Python爬虫-抓取的目标数据为#x开头,怎么解决?
前言 本文是该专栏的第4篇,后面会持续分享python爬虫案例干货,记得关注。 在做爬虫项目的时候,有时候抓取的平台目标数据为&#x开头,如下图所示: 浏览器显示的正常数据,但通过爬虫协议获取到的网页源码数据却是以&#x开头的隐藏数据,遇到这种情况,爬虫需要怎么处…...
短视频账号矩阵系统/技术开发搭建私有部署
本系统是基于短视频领域的新一代系统,旨在提供一个高效、全面的短视频管理与分发平台。系统采用先进的开发算法和技术,实现了智能化视频分类、推荐和用户互动功能。 目录 一、抖音SEO账号矩阵系统的开发和部署遵循以下原则: 二、账号矩阵绑…...

光致发光二极管光源——荧光效率检测系统
发光二极管(LED)光源已经逐步地取代传统光源,并在生产和生活中得以广泛应用。荧光粉在LED照明设备中起到了至关重要的作用,其功能为将转换芯片所产生的紫外或者蓝光,发射出目标颜色的光。近年来,人们为了提…...
【手撕C语言】多线程
(꒪ꇴ꒪ ),Hello我是祐言QAQ我的博客主页:C/C语言,Linux基础,ARM开发板,软件配置等领域博主🌍快上🚘,一起学习,让我们成为一个强大的攻城狮!送给自己和读者的一句鸡汤🤔&…...
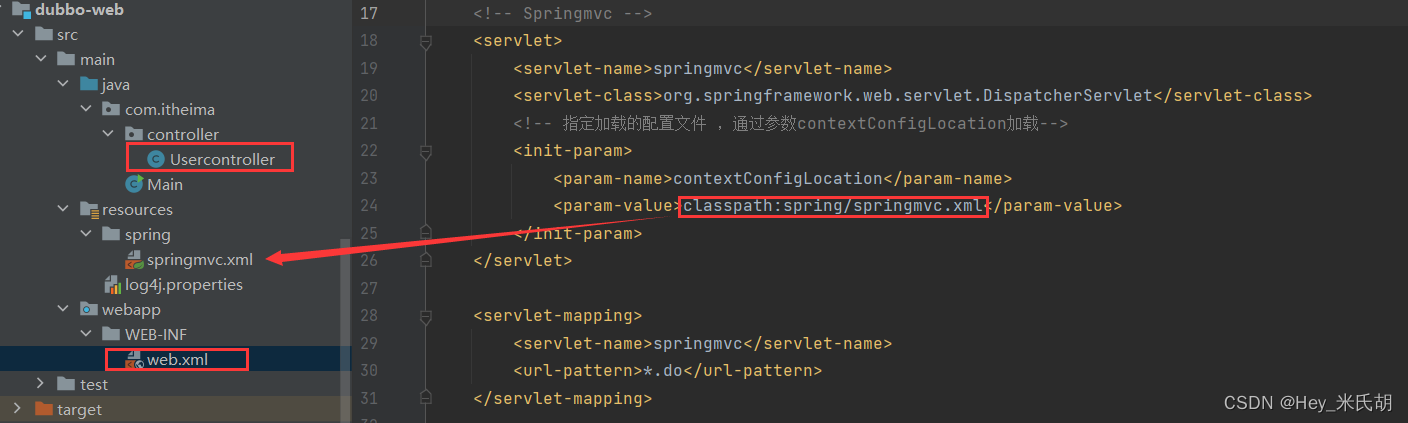
Dubbo2-概述
Dubbo 阿里公司开源的一个高性能,轻量级的javaRPC(远程服务调用方案)框架,提供高性能远程调用方案以及SOA服务治理方案 Dubbo架构 节点角色说明: Provider:服务提供方 Container:服务运行容器 Consumer:调用远程服务…...
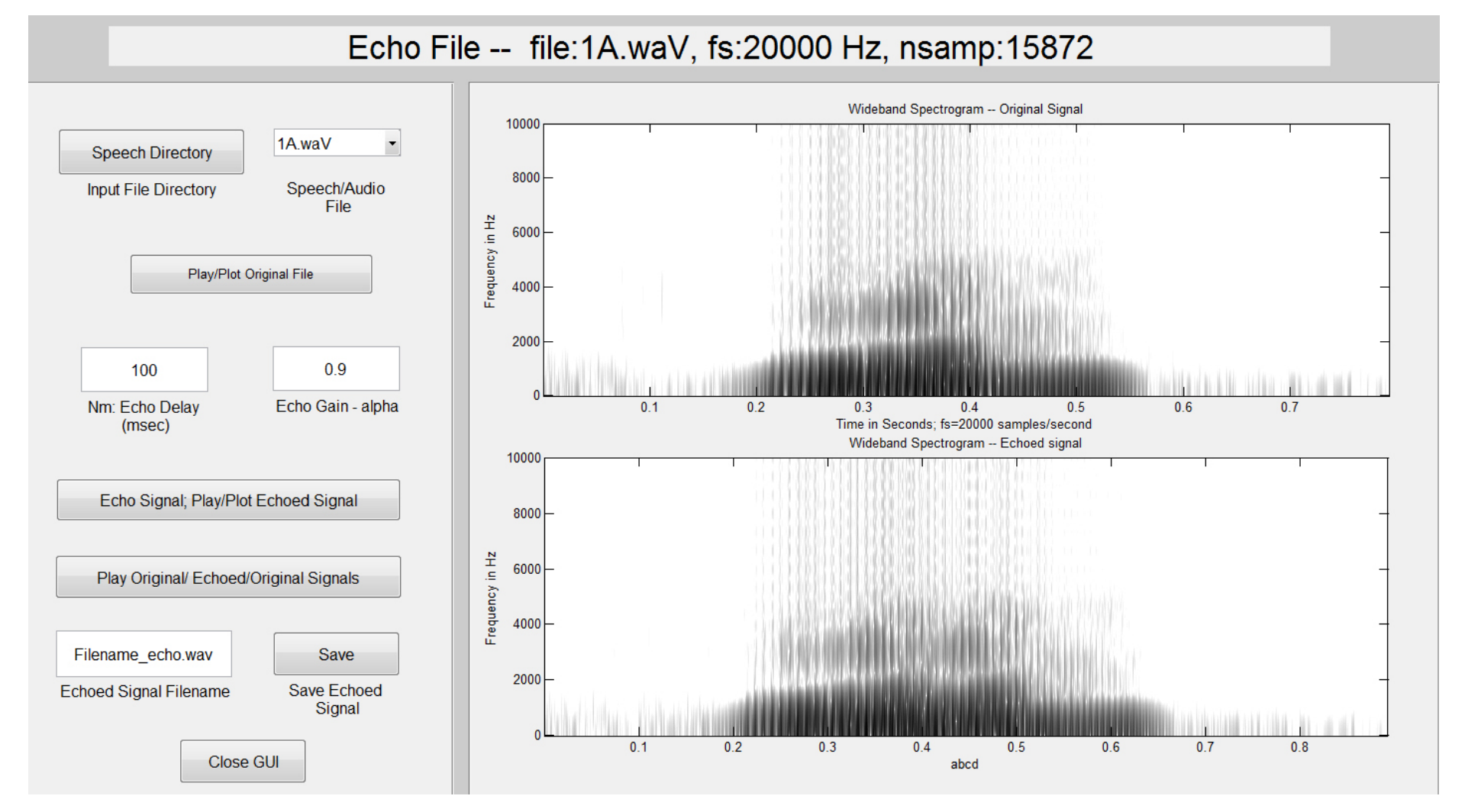
【将回声引入信号中】在语音或音频文件中引入混响或简单回声,以研究回声延迟和回波幅度对生成的回波信号感知的影响(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
pythonocc进阶学习:投影projection
1.点 到 线,(直线,曲线)等上的投影 staticmethod # 点到Lin的投影 def Project_Pnt_To_Lin(p: gp_Pnt, lin: gp_Lin):Edge BRepBuilderAPI_MakeEdge(lin).Edge()curve BRep_Tool.Curve(Edge)proPnt GeomAPI_ProjectPointOnCurve(p, curve[0])Neares…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...
