Monge矩阵
Monge矩阵
对一个m*n的实数矩阵A,如果对所有i,j,k和l,1≤ i<k ≤ m和1≤ j<l ≤ n,有 A[i,j]+A[k,l] ≤ A[i,l]+A[k,j] 那么,此矩阵A为Monge矩阵。
换句话说,每当我们从矩阵中挑出两行与两列,并且考虑行列交叉处的4个元素,左上角与右下角的和小于或等于左下角与右上角元素的和。
例如,下面这个就是一个Monge矩阵
(1)证明一个矩阵为Monge阵,当且仅当对所有i=1,2,...,m-1和j=1,2,...,n-1,有 A[i,j]+A[i+1,j+1] ≤ A[i,j+1]+A[i+1,j]
(提示:在当部分,对行、列分别使用归纳法。)
(2)下面的矩阵不是Monge阵。改变一个元素,把它变成Monge矩阵
37 23 22 32
21 6 27 10
53 34 30 31
32 13 9 6
43 21 15 8
很明显是要改27,27可以改成【2,5】内的任何一个实数
(3)假设f(i)是第i行包含最左端最小值的列的索引值。证明对任何的m x n Monge矩阵,有f(1) ≤ f(2) ≤...≤ f(m)。
(4)下面是一个用来计算m x n 的Monge矩阵A中每一行的最左最小值的分治算法的描述:
构造一个包含所有A的偶数行的子矩阵A'。递归地计算A'中每一行的最左端最小值。然后计算A中奇数行的最左端最小值。
解释如何能在O(m+n)时间内计算出A的奇数行的最左端最小值?(在偶数行最左最小值已知的情况下)
解释:看下面的代码就很明显了。
其实这个算法,我个人感觉,就结构而言比较像分治,但是就思想而言比较像动态规划。
(5)写出(4)所描述算法的运行时间的递归式,并证明其解为O(m+nlogm)
T(m)=T(m/2)+ O(m+n)(求解略)
我的代码:
#include<iostream>
using namespace std;void calculate(double **A, int r1, int r2, int min, int max, int *f) //计算f(r1)到f(r2)
{if (r1 > r2)return;int r = (r1 + r2) / 2;int result = min;int flag = A[r][min];for (int i = min + 1; i <= max; i++) //寻找最左最小元素flag,和它的的下标result{if (A[r][i] < flag){flag = A[r][i];result = i;}}f[r] = result;calculate(A, r1, r - 1, min, result, f);calculate(A, r + 1, r2, result, max, f);
}bool isMonge(double **A, int m, int n) //判断是否是Monge矩阵
{for (int i = 0; i < m - 1; i++)for (int j = 0; j < n - 1; j++)if (A[i][j] + A[i + 1][j + 1]>A[i + 1][j] + A[i][j + 1])return false;return true;
}
int main()
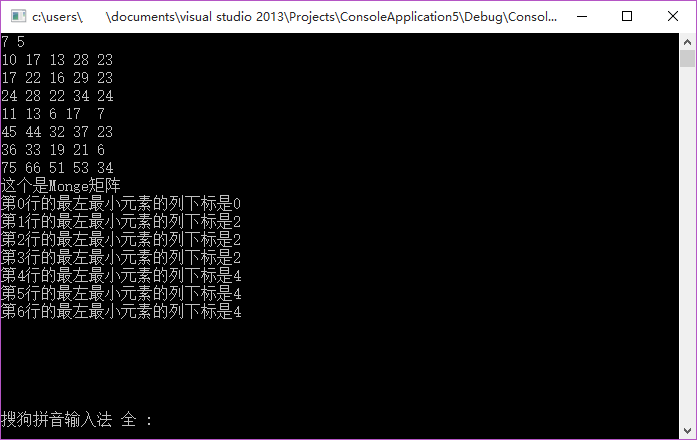
{int m, n;while (cin >> m >> n && m>1 && n > 1){double **A = new double*[m]; //Monge矩阵int *f = new int[m]; //不需要在主函数里面进行初始化,这个工作由calculate函数完成for (int i = 0; i < m; i++){A[i] = new double[n];for (int j = 0; j < n; j++)cin >> A[i][j];}if (isMonge(A, m, n)){cout << "这个是Monge矩阵" << endl;calculate(A, 0, m - 1, 0, n - 1, f);for (int i = 0; i < m; i++)cout << "第" << i << "行的最左最小元素的列下标是" << f[i] << endl;}else cout << "这个不是Monge矩阵";}return 0;
}相关文章:
Monge矩阵
Monge矩阵 对一个m*n的实数矩阵A,如果对所有i,j,k和l,1≤ i<k ≤ m和1≤ j<l ≤ n,有 A[i,j]A[k,l] ≤ A[i,l]A[k,j] 那么,此矩阵A为Monge矩阵。 换句话说,每当我们从矩阵中挑…...
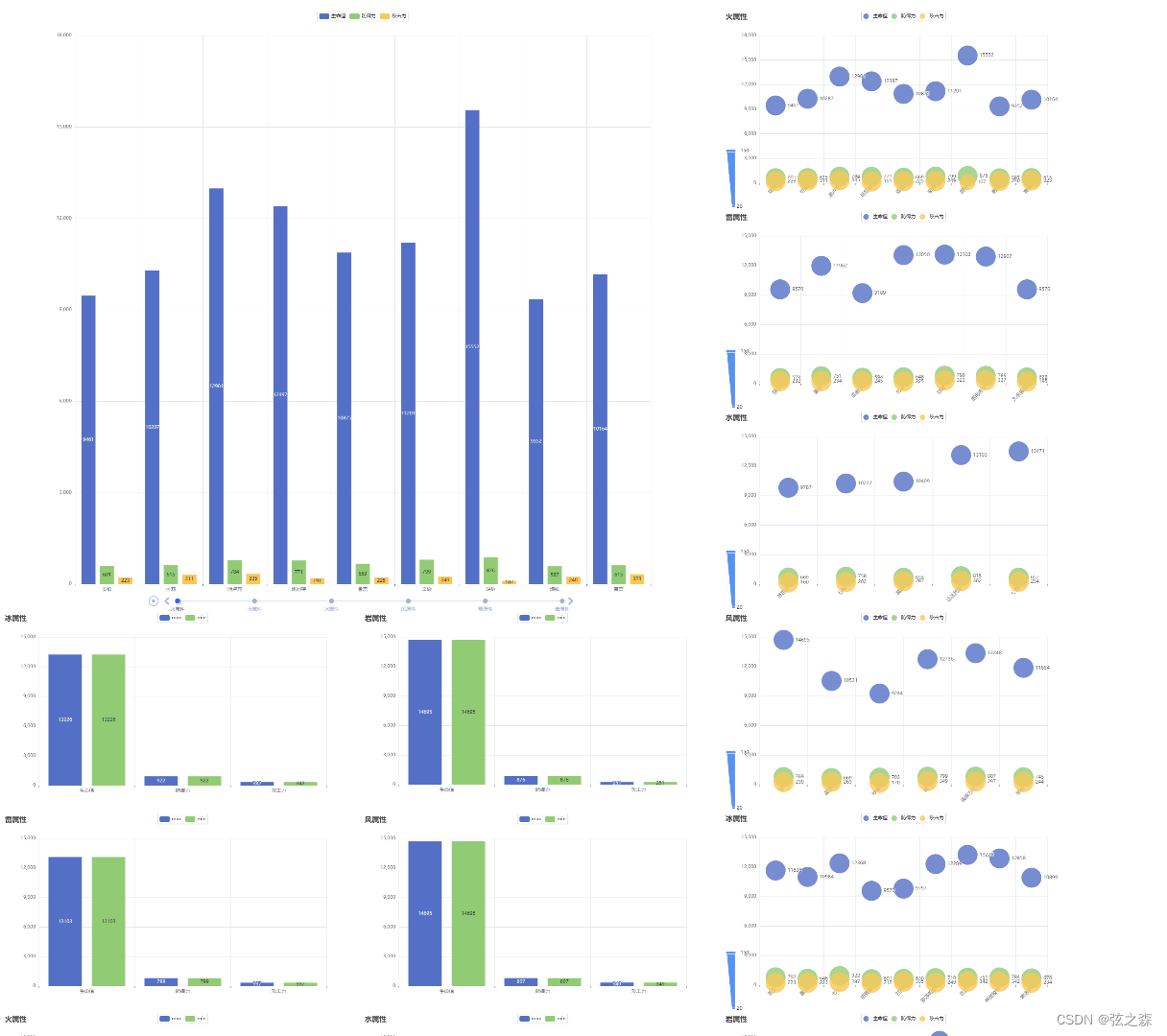
(5)所有角色数据分析页面的构建-5
所有角色数据分析页面,包括一个时间轴柱状图、六个散点图、六个柱状图(每个属性角色的生命值/防御力/攻击力的max与min的对比)。 """绘图""" from pyecharts.charts import Timeline from find_type import FindType import pandas …...
:专利撰写资料汇总)
专利进阶(三):专利撰写资料汇总
文章目录 一、前言二、资料汇总三、拓展阅读 一、前言 在专利撰写前,需要首先了解专利撰写所需遵守的基本规则。可以借助的撰写工具是什么。文献检索在哪里?注意事项是什么?本篇博文会就以上问题进行逐一解答。 专利撰写基本原则࿱…...

maven编译始终提示无效的目标发行版的解决方法
摘自个人印象笔记2021-05-07:https://app.yinxiang.com/fx/55e1d5f4-aeea-446a-a768-0f1a48195f5b(图显示不完整可查看原笔记内容)1:确保IDE中的编译版本正确 在idea中,主要看项目属性中和setting的java compiler中对应的jdk版本是否正确&…...

系统架构设计高级技能 · 软件可靠性分析与设计(三)【系统架构设计师】
系列文章目录 系统架构设计高级技能 软件架构概念、架构风格、ABSD、架构复用、DSSA(一)【系统架构设计师】 系统架构设计高级技能 系统质量属性与架构评估(二)【系统架构设计师】 系统架构设计高级技能 软件可靠性分析与设计…...
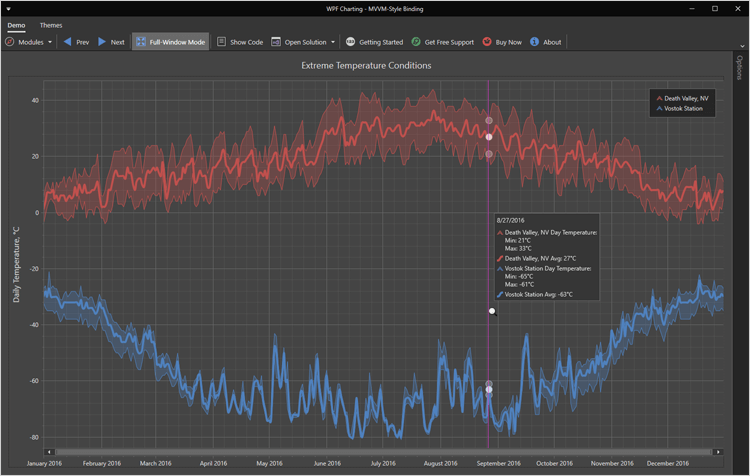
界面控件DevExpress WPF Chart组件——拥有超快的数据可视化库!
DevExpress WPF Chart组件拥有超大的可视化数据集,并提供交互式仪表板与高性能WPF图表库。DevExpress Charts提供了全面的2D / 3D图形集合,包括数十个UI定制和数据分析/数据挖掘选项。 PS:DevExpress WPF拥有120个控件和库,将帮助…...

【网络安全】等保测评安全物理环境
【网络安全】等保测评&安全物理环境 前言第1章 安全物理环境1.1 物理位置选择1.2 物理访问控制(高风险项)1.3 防盗窃1.4 防雷击1.5 防火1.6 防水防潮1.7 防静电1.8 温湿度控制1.9 电力供应1.10 电磁防护 前言 等级保护对象是由计算机或其他信息终端…...
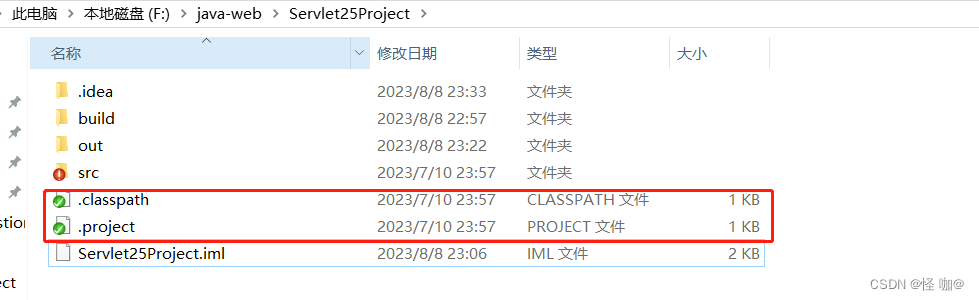
Intellij IDEA 导入 eclipse web 项目详细操作
Eclipse当中的web项目都会有这两个文件。但是idea当中应该是没有的,所以导入会出现兼容问题。但是本篇文章会教大家如何导入,并且导入过后还能使用tomcat运行。文章尽可能以图片的形式进行演示。我的idea使用的版本是2022.3.3版本。当然按正常来说版本之…...

安卓java A应用切换到B应用,来回切换不执行OnCreate
需求:安卓java如何做到A应用切换到B应用,如果B应用没启动就启动,如果B应用已经启动就仅仅切换到B应用。B应用再切换回A应用,不要重复执行OnCreate! 在 A 应用中的: 在 A 应用中,如果你希望在切换回 B 应用…...

【Linux】批量恢复文件权限
批量恢复文件权限 Linux 中,如果意外误操作将根目录目录权限批量设置,比如 chmod -R 777 / ,系统中的大部分服务以及命令将无法使用,这时候可以通过系统自带的 getfacl 命令来拷贝和还原系统权限,若是其他系统目录被误…...
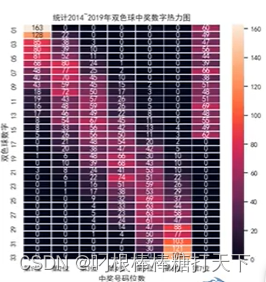
数据可视化(八)堆叠图,双y轴,热力图
1.双y轴绘制 #双Y轴可视化数据分析图表 #add_subplot() dfpd.read_excel(mrbook.xlsx) x[i for i in range(1,7)] y1df[销量] y2df[rate] #用来正常显示负号 plt.rcParams[axes.unicode_minus]False figplt.figure() ax1fig.add_subplot(1,1,1)#一行一列,第一个区域…...

前台自动化测试:基于敏捷测试驱动开发(TDD)的自动化测试原理
一、自动化测试概述 自动化测试主要应用到查询结果的自动化比较,把借助自动化把相同的数据库数据的相同查询条件查询到的结果同理想的数据进行自动化比较或者同已经保障的数据进行不同版本的自动化比较,减轻人为的重复验证测试。多用户并发操作需要自动…...

基于SLAM的规划算法仿真复现|SLAM|智能规划
图片来自百度百科 前言 那么这里博主先安利一些干货满满的专栏了! 首先是博主的高质量博客的汇总,这个专栏里面的博客,都是博主最最用心写的一部分,干货满满,希望对大家有帮助。 高质量博客汇总https://blog.csdn.n…...

sqlite3多线程操作问题
在项目中使用sqlite3,有时会报database is locked 两种方式 1、多线程读,多线程写,只使用共同一个数据库连接,即使用同一个SQLiteHelper连接,调用sqlite3_busy_timeout 2、多线程读,单线程写,每…...

ACCESS数据库增删改查
[添加COM组件] A: Microsoft ADO Ext. 2.8 for DDL and Security B: Microsoft ActiveX Data Objects 2.8 Library [添加头文件]using System.Data.OleDb; using System.Data; using ADOX; using System.IO; using System; using System.Collections.Generic; using System.L…...
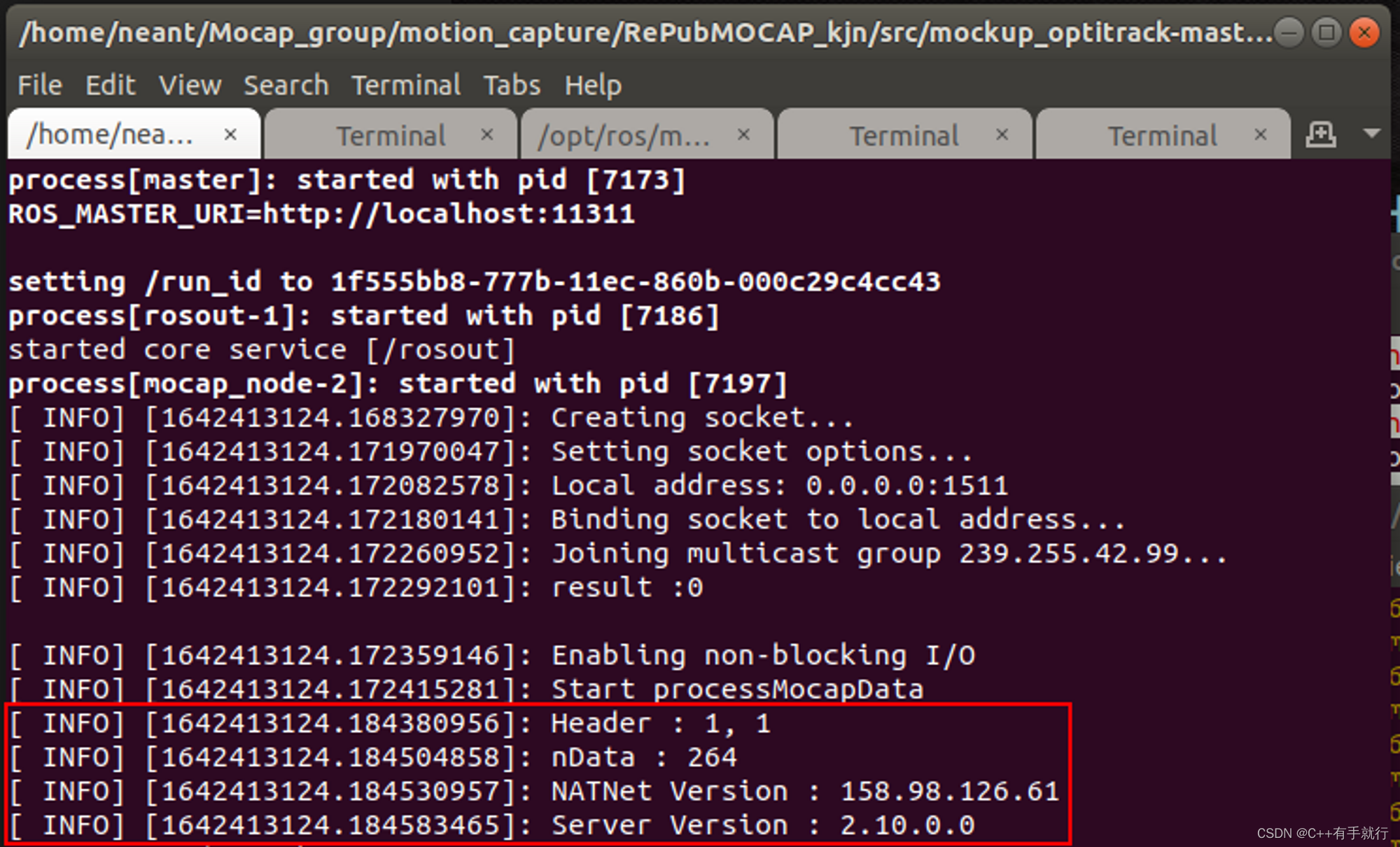
动捕系统mockup_optitrack替换为VRPN传递信息
motive:启动→载入已有→layout选择capture→view选择data streming→复选marker右键create刚体→rename刚体→修改local interface为本机ip→勾选vrpn ROS端:roslaunch vrpn_client_ros vrpn_efy.launch 记得修改server地址为motiveip地址 关掉motive…...
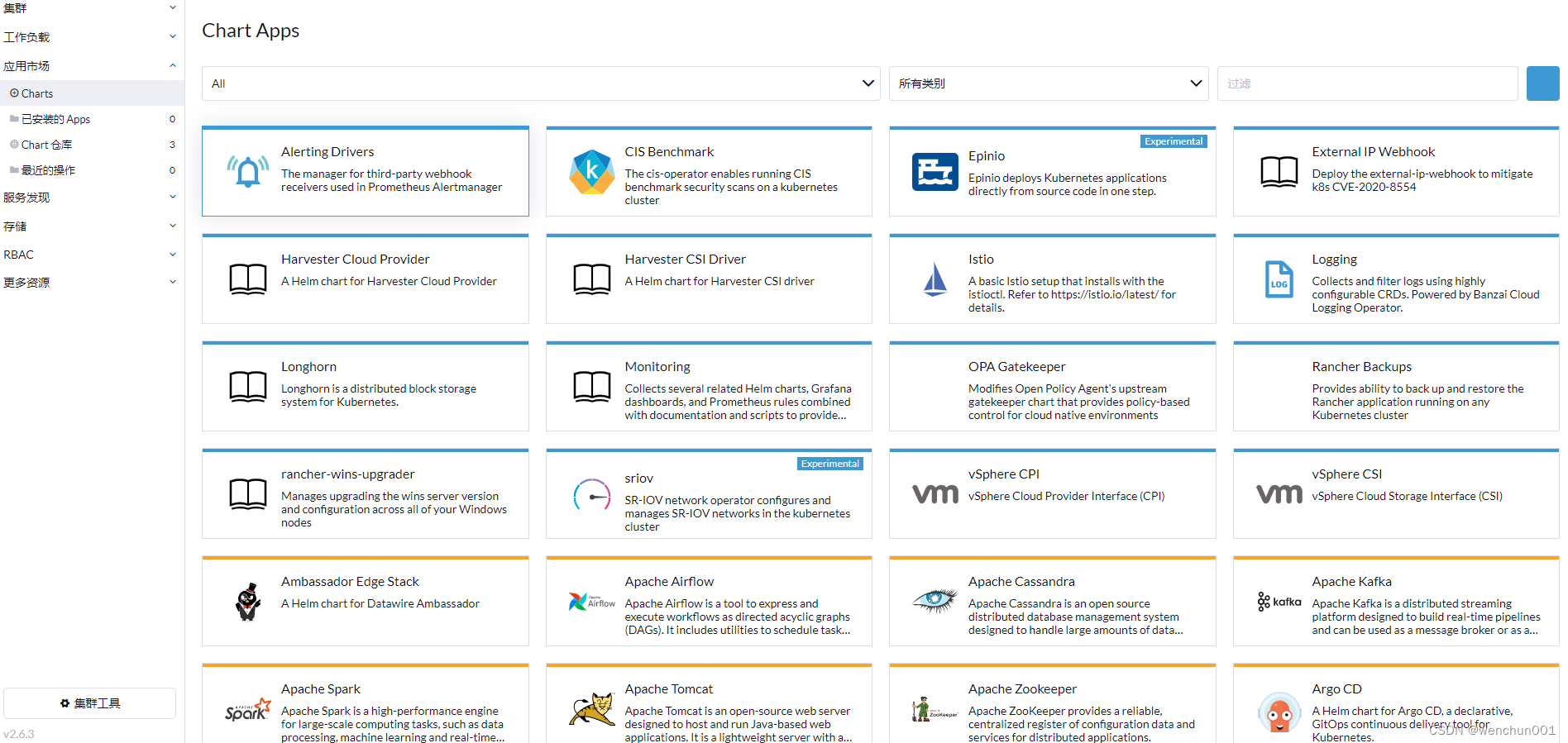
【服务平台】Rancher运行和管理Docker和Kubernetes,提供管理生产中的容器所需的整个软件堆栈
Rancher是一个开源软件平台,使组织能够在生产中运行和管理Docker和Kubernetes。使用Rancher,组织不再需要使用一套独特的开源技术从头开始构建容器服务平台。Rancher提供了管理生产中的容器所需的整个软件堆栈。 完整软件堆栈 Rancher是供采用容器的团…...

二叉树的完全性检验
给定一个二叉树的 root ,确定它是否是一个 完全二叉树 。 在一个 完全二叉树 中,除了最后一个关卡外,所有关卡都是完全被填满的,并且最后一个关卡中的所有节点都是尽可能靠左的。它可以包含 1 到 2h 节点之间的最后一级 h 。 示…...

激活函数总结(六):ReLU系列激活函数补充(RReLU、CELU、ReLU6)
激活函数总结(六):ReLU系列激活函数补充 1 引言2 激活函数2.1 RReLU激活函数2.2 CELU激活函数2.3 ReLU6 激活函数 3. 总结 1 引言 在前面的文章中已经介绍了介绍了一系列激活函数 (Sigmoid、Tanh、ReLU、Leaky ReLU、PReLU、Swish、ELU、SEL…...
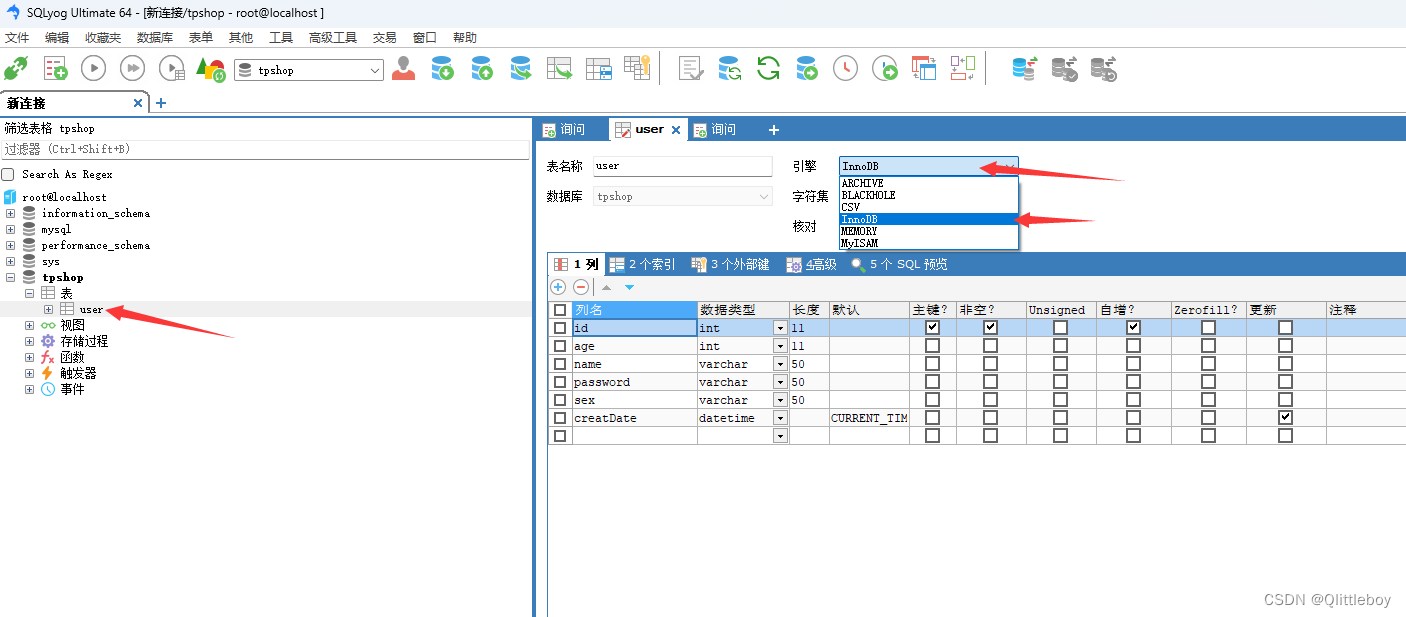
tp5中的事务处理
使用事务首先要数据库支持事务; 如下MySQL数据库user表开启事务支持,即设计表->引擎设置为InnoDB->保存 事务处理 1. 数据库的表引擎需要是 InnoDB 才可以使用,如果不是调整即可; 2. 事务处理,需要执行多个 SQ…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...

根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的----NTFS源代码分析--重要
根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的 第一部分: 0: kd> g Breakpoint 9 hit Ntfs!ReadIndexBuffer: f7173886 55 push ebp 0: kd> kc # 00 Ntfs!ReadIndexBuffer 01 Ntfs!FindFirstIndexEntry 02 Ntfs!NtfsUpda…...

django blank 与 null的区别
1.blank blank控制表单验证时是否允许字段为空 2.null null控制数据库层面是否为空 但是,要注意以下几点: Django的表单验证与null无关:null参数控制的是数据库层面字段是否可以为NULL,而blank参数控制的是Django表单验证时字…...

elementUI点击浏览table所选行数据查看文档
项目场景: table按照要求特定的数据变成按钮可以点击 解决方案: <el-table-columnprop"mlname"label"名称"align"center"width"180"><template slot-scope"scope"><el-buttonv-if&qu…...



