数据结构 | 树的定义及实现
目录
一、树的术语及定义
二、树的实现
2.1 列表之列表
2.2 节点与引用
一、树的术语及定义
节点:
节点是树的基础部分。它可以有自己的名字,我们称作“键”。节点也可以带有附加信息,我们称作“有效载荷”。有效载荷信息对于很多树算法来说不是重点,但它常常在使用树的应用中很重要。
边:
边是树的另一个基础部分。两个节点通过一条边相连,表示他们之间存在关系。除了根节点以外,其他每个节点都仅有一条入边,出边则可能有多条。
根节点:
根节点是树中唯一没有入边的节点。
路径:
路径是由边连接的有序节点列表。比如,哺乳纲食肉目
猫科
猫属
家猫就是一条路径。
子节点:
一个节点通过出边和子节点相连。
父节点:
一个节点是其所有子节点的父节点。
兄弟节点:
具有同一父节点的节点互称为兄弟节点。
子树:
一个父节点及其所有后代的节点和边构成一颗子树。
叶子节点:
叶子节点没有子节点。
层数:
节点n的层数是从根节点到n的唯一路径长度。根节点的层数是0。
高度:
树的高度是其中节点层数的最大值。
定义基本术语后,就可以进一步给出树的正式定义。实际上,下面提供了两种定义,其中一种涉及节点和边,另一种涉及递归。递归定义很有用。
定义一:树由节点及连接节点的边构成。树有以下属性:
- 有一个根节点;
- 除根节点外,其他每个节点都与其唯一的父节点相连;
- 从根节点到其他每个节点都有且仅有一条路径;
- 如果每个节点最多有两个子节点,我们就称这样的树为二叉树。
定义二:一棵树要么为空,要么由一个根节点和零颗或多颗子树构成,子树本身也是一棵树。每颗子树的根节点通过一条边连到父树的根节点。
二、树的实现
根据上面的定义,可以使用以下函数创建并操作二叉树。
- BinaryTree()创建一个二叉树实例。
- getLeftChild()返回当前节点的左子节点所对应的二叉树。
- getRightChild()返回当前节点的右子节点所对应的二叉树。
- setRootVal(val)在当前节点中存储参数val中的对象。
- getRootVal()返回当前节点存储的对象。
- insertLeft(val)新建一颗二叉树,并将其作为当前节点的左子节点。
- insertRight(val)新建一颗二叉树,并将其作为当前节点的右子节点。
实现树的关键在于选择一个好的内部存储技巧。Python提供两种有意思的方式,我们在选择前会仔细了解这两种方式。第一种称作“列表之列表”,第二种称作“节点与引用”。
2.1 列表之列表
在“列表之列表”的树中,我们将根节点的值作为列表的第一个元素;第二个元素是代表左子树的列表;第三个元素是代表右子树的列表。
myTree=['a', #根节点['b', #左子树['d',[],[]],['e',[],[]] ],['c', #右子树['f',[],[]],[] ]]注意,可以通过标准的列表切片操作访问子树。树的根节点是myTree[0],左子树是myTree[1],右子树是myTree[2]。“列表之列表”表示法有个很好的性质,那就是表示子树的列表结构很符合树的定义,这样的结构是递归的!由一个根节点和两个空列表构成的子树是一个叶子节点。还有一个很好的性质,那就是这种表示法可以推广到有很多子树的情况。如果树不是二叉树,则多一个子树只是多一个列表。

接下来提供一些便于将列表作为树使用的函数,以正式定义树数据结构。注意,我们不是要定义二叉树类,而是要创建可用于标准列表的函数。
列表的函数BinaryTree:
def BinaryTree(r):return [r,[],[]]BinaryTree函数构造一个简单的列表,它仅有一个根节点和两个作为子节点的空列表。要给树添加左子树,需要在列表的第二个位置加入一个新的列表。请务必当心:如果列表的第二个位置已经有内容了,我们要保留已有内容,并将它作为新列表的左子树。
插入左子树的Python代码:
def insertLeft(root,newBranch):t=root.pop(1)if len(t)>1:root.insert(1,[newBranch,t,[]])else:root.insert(1,[newBranch,[],[]])return root插入右子树的Python代码:
def insertRight(root,newBranch):t=root.pop(2)if len(t)>1:root.insert(2,[newBranch,[],t])else:root.insert(2,[newBranch,[],[]])return root为了完整地创建树的函数集,我们编写一些访问函数,用于读写根节点与左右子树。
树的访问函数代码:
def getRootVal(root):return root[0]def setRootVal(root,newVal):root[0]=newValdef getLeftChild(root):return root[1]def getRightChild(root):return root[2]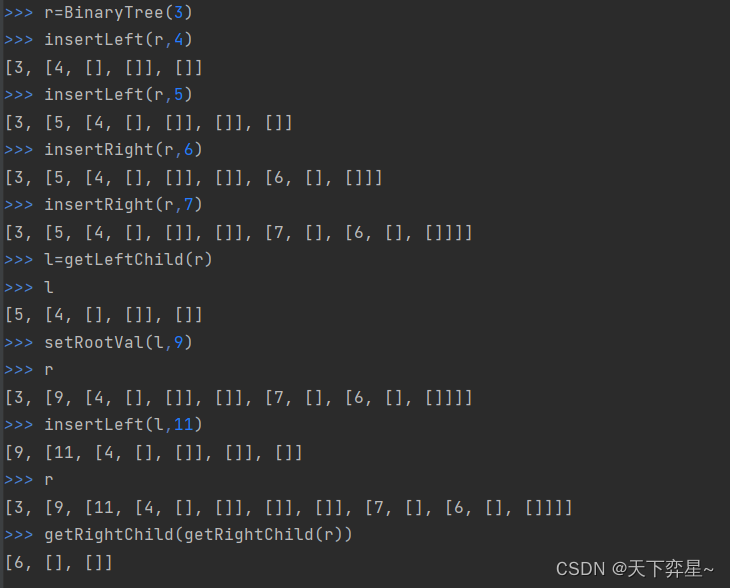
2.2 节点与引用
树的第二种表示法是利用节点与引用。我们将定义一个类,其中有根节点和左右子树的属性。这种表示法遵循对象编程范式。
#BinaryTree类
class BinaryTree:def __init__(self,rootObj):self.key=rootObjself.leftChild=Noneself.rightChild=None#插入左子节点def insertLeft(self,newNode):if self.leftChild==None:self.leftChild=BinaryTree(newNode)else:t=BinaryTree(newNode)t.left=self.leftChildself.leftChild=t#插入右子节点def insertRight(self,newNode):if self.rightChild==None:self.rightChild=BinaryTree(newNode)else:t=BinaryTree(newNode)t.right=self.rightChildself.rightChild=t#二叉树的访问函数def getRightChild(self):return self.rightChilddef getLeftChild(self):return self.leftChilddef setRootVal(self,obj):self.key=objdef getRootVal(self):return self.key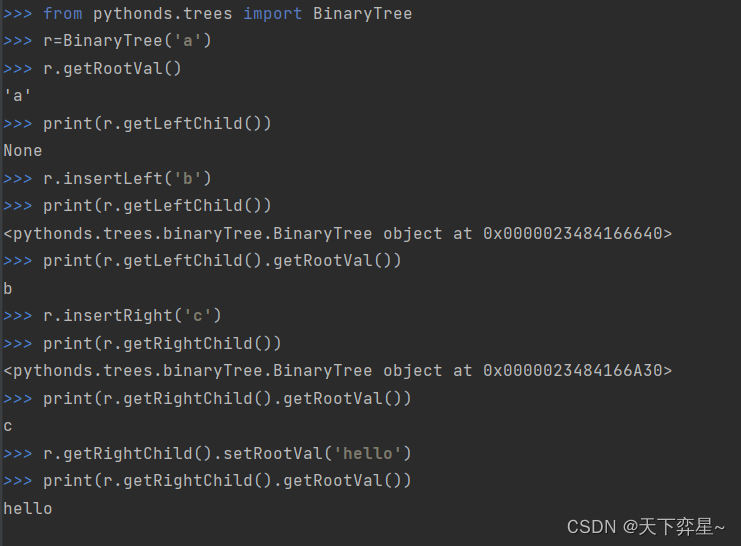
相关文章:

数据结构 | 树的定义及实现
目录 一、树的术语及定义 二、树的实现 2.1 列表之列表 2.2 节点与引用 一、树的术语及定义 节点: 节点是树的基础部分。它可以有自己的名字,我们称作“键”。节点也可以带有附加信息,我们称作“有效载荷”。有效载荷信息对于很多树算法…...
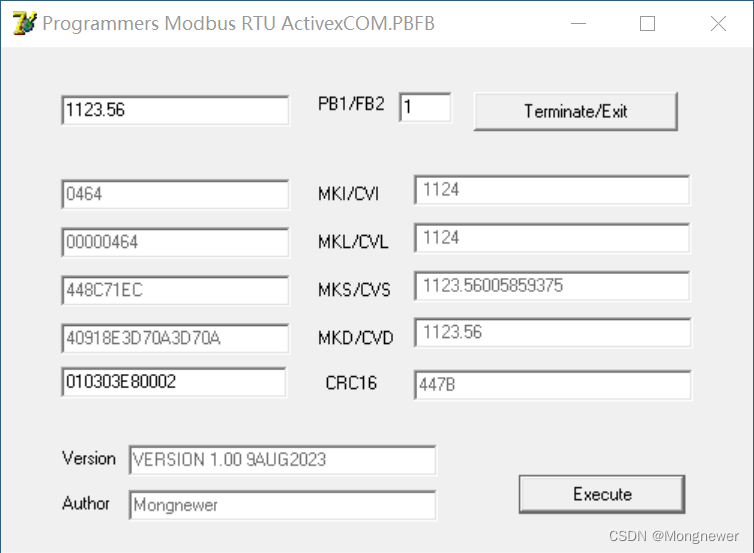
Delphi7通过VB6之COM对象调用FreeBASIC写的DLL功能
VB6写ActiveX COM组件比较方便,不仅PowerBASIC与VB6兼容性好,Delphi7与VB6兼容性也不错,但二者与FreeBASIC兼容性在字符串处理上差距比较大,FreeBASIC是C化的语言,可直接使用C指令。下面还是以实现MKI/CVI, MKL/CVL, M…...
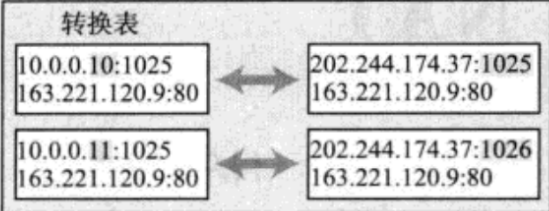
【Linux 网络】NAT技术——缓解IPv4地址不足
NAT技术 NAT 技术背景NAT IP转换过程NAPTNAT 技术的缺陷 NAT(Network Address Translation,网络地址转换)技术,是解决IP地址不足的主要手段,并且能够有效地避免来自网络外部的攻击,隐藏并保护网络内部的计算…...
协议)
Flink 两阶段提交(Two-Phase Commit)协议
Flink 两阶段提交(Two-Phase Commit)是指在 Apache Flink 流处理框架中,为了保证分布式事务的一致性而采用的一种协议。它通常用于在流处理应用中处理跨多个分布式数据源的事务性操作,确保所有参与者(数据源或计算节点…...

【Docker晋升记】No.2 --- Docker工具安装使用、命令行选项及构建、共享和运行容器化应用程序
文章目录 前言🌟一、Docker工具安装🌟二、Docker命令行选项🌏2.1.docker run命令选项:🌏2.2.docker build命令选项:🌏2.3.docker images命令选项:🌏2.4.docker ps命令选项…...

[OnWork.Tools]系列 00-目录
OnWork.Tools系列文章目录 OnWork.Tools系列 01-简介_末叶的博客-CSDN博客OnWork.Tools系列 02-安装_末叶的博客-CSDN博客OnWork.Tools系列 03-软件设置_末叶的博客-CSDN博客OnWork.Tools系列 04-快捷启动_末叶的博客-CSDN博客OnWork.Tools系列 05-系统工具_末叶的博客-CSDN博…...

Cadvisor+InfluxDB+Grafan+Prometheus(详解)
目录 一、CadvisorInfluxDBGrafan案例概述 (一)Cadvisor Cadvisor 产品特点: (二)InfluxDB InfluxDB应用场景: InfluxDB主要功能: InfluxDB主要特点: (三&#…...
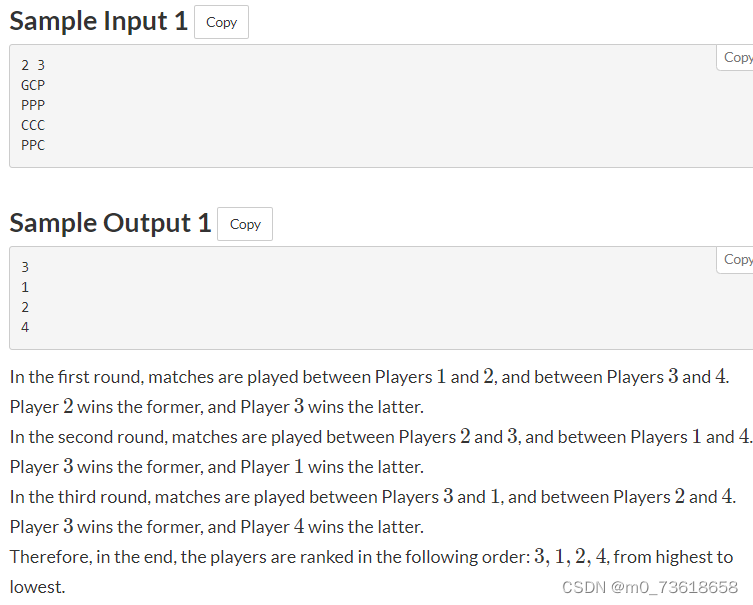
AtcoderABC222场
A - Four DigitsA - Four Digits 题目大意 给定一个整数N,其范围在0到9999之间(包含边界)。在将N转换为四位数的字符串后,输出它。如果N的位数不足四位,则在前面添加必要数量的零。 思路分析 可以使用输出流的格式设…...
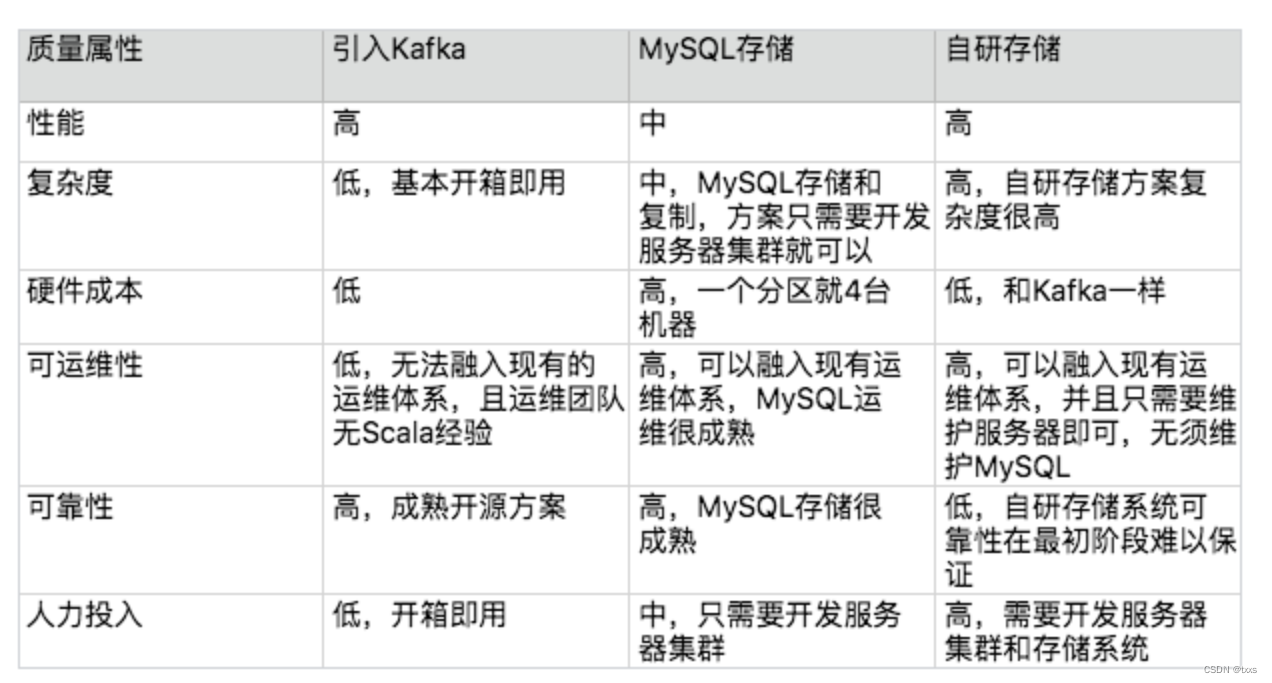
架构实践方法
一、识别复杂度 将主要的复杂度问题列出来,然后根据业务、技术、团队等综合情况进行排序,优先解决当前面临的最主要的复杂度问题。对于按照复杂度优先级解决的方式,存在一个普遍的担忧:如果按照优先级来解决复杂度,可…...
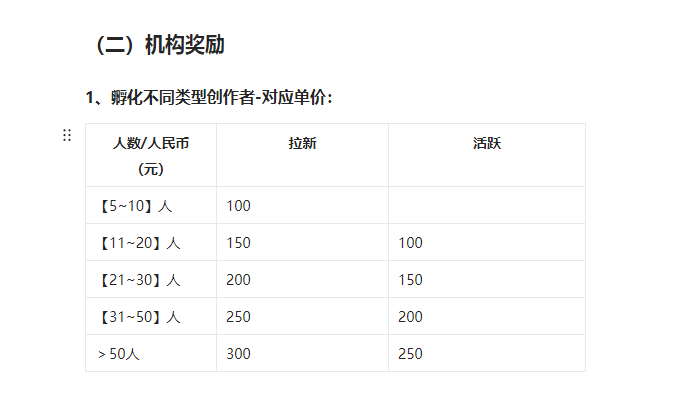
点淘的MCN机构申请详细入驻指南!
消费趋势的变化,来自消费人群的变化。 后疫情时代,经济复苏的反弹力度不足,人们开始怀疑我们正从前几年的消费升级,跌入消费降级的时代,但这并不能准确概括消费市场的变化。 仔细翻看各大奢侈品集团的财报࿰…...
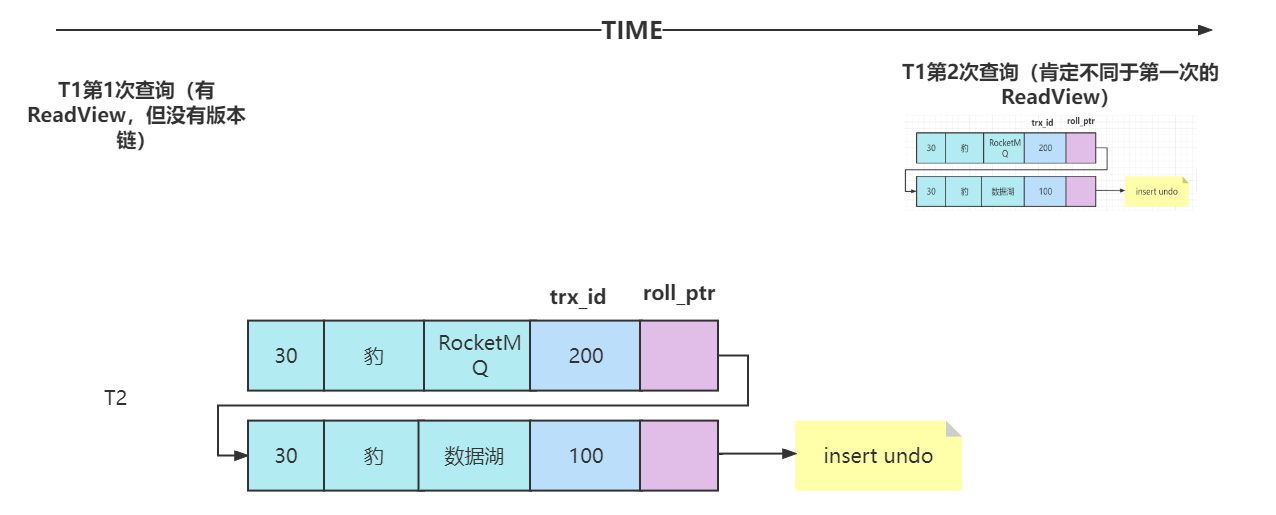
事务和事务的隔离级别
1.4.事务和事务的隔离级别 1.4.1.为什么需要事务 事务是数据库管理系统(DBMS)执行过程中的一个逻辑单位(不可再进行分割),由一个有限的数据库操作序列构成(多个DML语句,select语句不包含事务&…...
)
每日一题 34在排序数组中查找元素的第一个和最后一个位置(二分查找)
题目 给你一个按照非递减顺序排列的整数数组 nums,和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。 如果数组中不存在目标值 target,返回 [-1, -1]。 你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。 示例 1&…...
Spring Boot Admin 环境搭建与基本使用
Spring Boot Admin 环境搭建与基本使用 一、Spring Boot Admin是什么二、提供了那些功能三、 使用Spring Boot Admin3.1搭建Spring Boot Admin服务pom文件yml配置文件启动类启动admin服务效果 3.2 common-apipom文件feignhystrix 3.3服务消费者pom文件yml配置文件启动类control…...
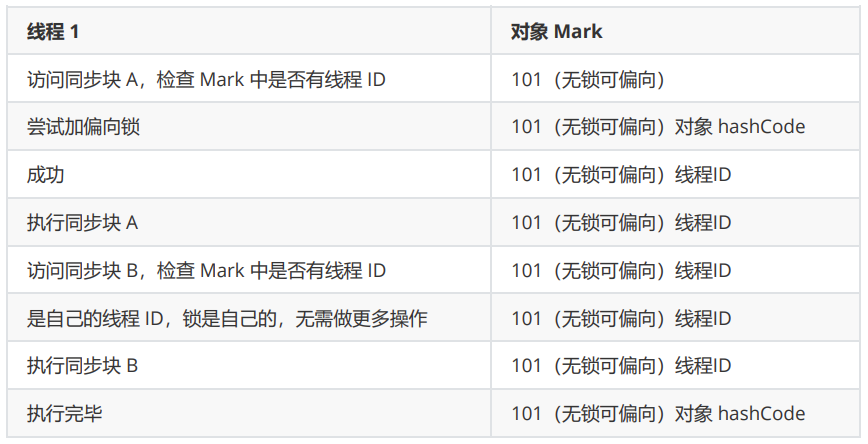
JVM之内存模型
1. Java内存模型 很多人将Java 内存结构与java 内存模型傻傻分不清,java 内存模型是 Java Memory Model(JMM)的意思。 简单的说,JMM 定义了一套在多线程读写共享数据时(成员变量、数组)时,对数据…...

音视频 vs2017配置FFmpeg
vs2017 ffmpeg4.2.1 一、首先我把FFmpeg整理了一下,放在C盘 二、新建空项目 三、添加main.cpp,将bin文件夹下dll文件拷贝到cpp目录下 #include<stdio.h> #include<iostream>extern "C" { #include "libavcodec/avcodec.h&…...

【项目管理】PMP备考宝典-第二章《环境》
第一节:概述 1.项目所处的组织环境 (1)事业环境因素(EEFs) 组织内部的事业环境因素: 企业都会有愿景、使命、价值观,这些决定了企业的发展方向。不忘初心,坚定地走自己的路&#…...
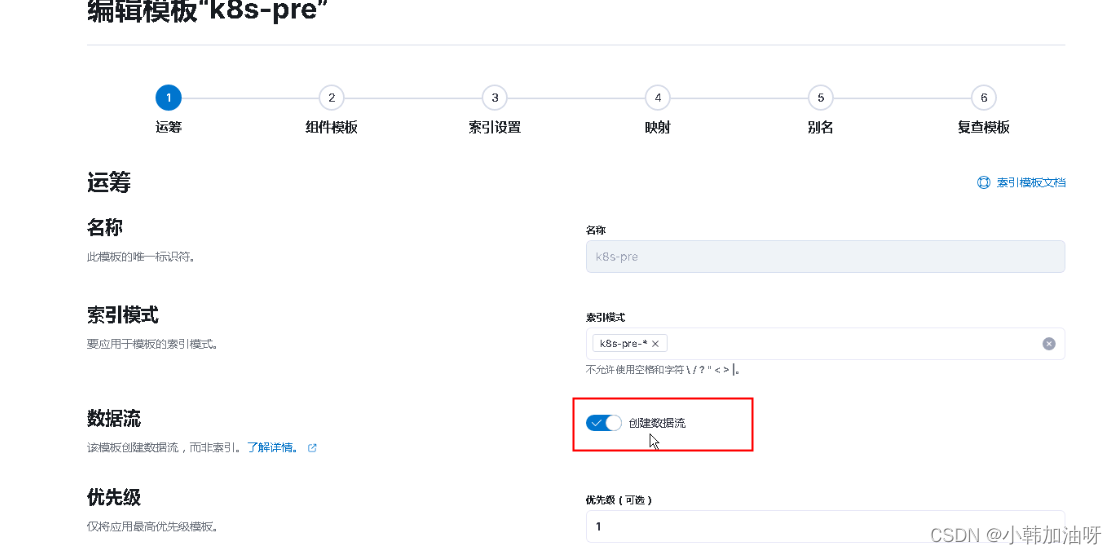
ELK 将数据流转换回常规索引
ELK 将数据流转换回常规索引 现象:创建索引模板是打开了数据流,导致不能创建常规索引,并且手动修改、删除索引模板失败 "reason" : "composable template [logs_template] with index patterns [new-pattern*], priority [2…...
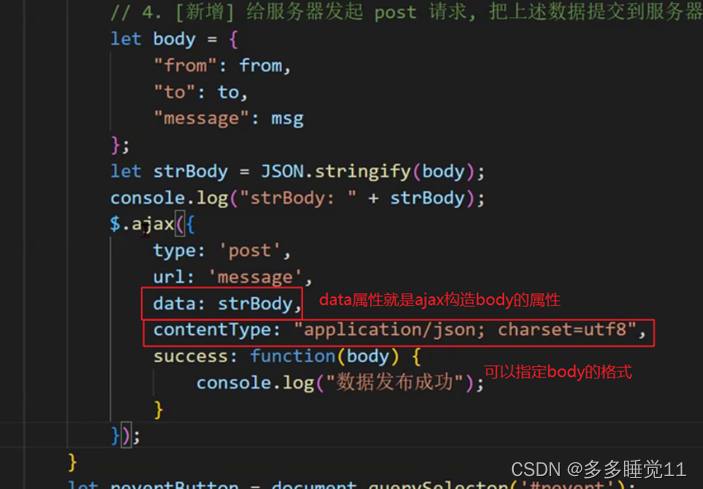
jackson库收发json格式数据和ajax发送json格式的数据
一、jackson库收发json格式数据 jackson库是maven仓库中用来实现组织json数据功能的库。 json格式 json格式一个组织数据的字符文本格式,它用键值对的方式存贮数据,json数据都是有一对对键值对组成的,键只能是字符串,用双引号包…...

ubuntu安装和卸载CLion
安装 在https://www.jetbrains.com/clion/download/#sectionlinux下载相应版本的安装包,解压之后,找到解压文件夹中的bin文件夹运行./clion.sh 卸载 使用sudo rm -rf删除以下内容;并把刚刚解压的文件删掉 ~/.config/JetBrains ~/.local/s…...
Petrel解释二维浅地层数据
Petrel是斯伦贝谢开发的一款地质解释和建模软件,有点像地理信息系统的ArcGIS,主要用于数据分析和展示。它不是用来处理原始数据的,而是集成各种处理后的结果数据进行特征分析和目标拾取。当然,它也能读取原始数据,比如…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

基于Java+VUE+MariaDB实现(Web)仿小米商城
仿小米商城 环境安装 nodejs maven JDK11 运行 mvn clean install -DskipTestscd adminmvn spring-boot:runcd ../webmvn spring-boot:runcd ../xiaomi-store-admin-vuenpm installnpm run servecd ../xiaomi-store-vuenpm installnpm run serve 注意:运行前…...

日常一水C
多态 言简意赅:就是一个对象面对同一事件时做出的不同反应 而之前的继承中说过,当子类和父类的函数名相同时,会隐藏父类的同名函数转而调用子类的同名函数,如果要调用父类的同名函数,那么就需要对父类进行引用&#…...

深入理解Optional:处理空指针异常
1. 使用Optional处理可能为空的集合 在Java开发中,集合判空是一个常见但容易出错的场景。传统方式虽然可行,但存在一些潜在问题: // 传统判空方式 if (!CollectionUtils.isEmpty(userInfoList)) {for (UserInfo userInfo : userInfoList) {…...
