重建二叉树
输入一棵二叉树前序遍历和中序遍历的结果,请重建该二叉树。
注意:
- 二叉树中每个节点的值都互不相同;
- 输入的前序遍历和中序遍历一定合法;
数据范围
树中节点数量范围 [0,100]
。
样例
给定:
前序遍历是:[3, 9, 20, 15, 7]
中序遍历是:[9, 3, 15, 20, 7]返回:[3, 9, 20, null, null, 15, 7, null, null, null, null]
返回的二叉树如下所示:3/ \9 20/ \15 7
代码:
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode(int x) : val(x), left(NULL), right(NULL) {}* };*/
class Solution {
public:unordered_map<int,int> pos; //用hash表记录每个点在中序遍历的位置vector<int> _preorder,_inorder; //动态数组存储前序遍历和中序遍历,用于创建树TreeNode* build(int a,int b,int x,int y) //创建数{if(a>b) return NULL; //区间为空的时候auto root=new TreeNode(_preorder[a]); //创建根节点int k=pos[root->val]; //子树根节点在中序遍历序列的位置// int k=-1,i=0;// while(_inorder[i]!=root->val){// i++;// }// k=i;root->left=build(a+1,k-1-x+a+1,x,k-1); root->right=build(k-1-x+a+1+1,b,k+1,y);return root; //返回根节点}TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {_preorder=preorder,_inorder=inorder;int n=inorder.size();for(int i=0;i<n;i++) pos[_inorder[i]]=i;return build(0,n-1,0,n-1); //返回递归结果}
};相关文章:

重建二叉树
输入一棵二叉树前序遍历和中序遍历的结果,请重建该二叉树。 注意: 二叉树中每个节点的值都互不相同;输入的前序遍历和中序遍历一定合法; 数据范围 树中节点数量范围 [0,100] 。 样例 给定: 前序遍历是:[3, 9, 2…...

支付整体架构
5.4 支付的技术架构 架构即未来,只有建立在技术架构设计良好的体系上,支付机构才能有美好的未来。如果支付的技术体系在架构上存在问题,那么就没有办法实现高可用性、高安全性、高效率和水平可扩展性。 总结多年来在海内外支付机构主持和参与…...

百度智能云:千帆大模型平台接入Llama 2等33个大模型,上线103个Prompt模板
大家好,我是herosunly。985院校硕士毕业,现担任算法研究员一职,热衷于机器学习算法研究与应用。曾获得阿里云天池比赛第一名,CCF比赛第二名,科大讯飞比赛第三名。拥有多项发明专利。对机器学习和深度学习拥有自己独到的…...
烦人的幻灯片——拓扑排序
烦人的幻灯片 烦人的幻灯片问题描述输入输出格式输入格式输出格式 输入输出样例输入样例:输入样例一:输入样例二: 输出样例:输出样例一:输出样例二: 正确做法拓扑排序 代码 烦人的幻灯片 问题描述 李教授…...

无涯教程-Perl - ord函数
描述 此函数返回EXPR指定的字符的ASCII数值,如果省略则返回$_。例如,ord(A)返回值为65。 语法 以下是此函数的简单语法- ord EXPRord返回值 该函数返回整数。 例 以下是显示其基本用法的示例代码- #!/usr/bin/perl -wprint("ord() ", ord(G), "\n"…...

Python爬虫:js逆向调式操作及调式中遇到debugger问题
Python爬虫:js逆向调式操作及调式中遇到debugger问题 1. 前言2. js逆向调式操作2.1 DOM事件断点2.2 XHR/提取断点(用于请求接口参数加密处理)2.3 请求返回的数据是加密的2.4 hook定位参数 3. 调式中遇到debugger问题3.1 解决方式(一律不在此处暂停)3.2 问题:点击一律…...

HTML网页制作技巧:打造出色的用户体验
HTML是构建网页的基础语言,掌握一些关键的技巧可以帮助您创建出色的用户体验。本文将介绍一些HTML网页制作的技巧,从布局和样式到交互和可访问性,为您提供有用的指导。无论您是初学者还是有经验的开发者,这些技巧都将对您的网页设…...

探究使用HTTP代理ip后无法访问网站的原因与解决方案
目录 访问网站的原理是什么 1. DNS解析 2. 建立TCP连接 3. 发送HTTP请求: 4. 服务器响应: 5. 浏览器渲染: 6. 页面展示: 使用代理IP后访问不了网站,有哪些方面的原因 1. 代理IP的可用性: 2. 代理…...

SpringBoot 全局异常处理进阶
待总结 参考文章: SpringBoot 全局异常处理进阶:使用 ControllerAdvice 对不同的 Controller 分别捕获异常并处理 SpringBoot 对 controller 层捕获全局异常并处理的方法(ControllerAdvice 和 ExceptionHandler) 注解RestCont…...

数据结构(一):顺序表详解
在正式介绍顺序表之前,我们有必要先了解一个名词:线性表。 线性表: 线性表是,具有n个相同特性的数据元素的有限序列。常见的线性表:顺序表、链表、栈、队列、数组、字符串... 线性表在逻辑上是线性结构,但…...

【周末闲谈】人工智能热潮下的AIGC到底指的是什么?
生成式人工智能AIGC(Artificial Intelligence Generated Content)是人工智能1.0时代进入2.0时代的重要标志。 个人主页:【😊个人主页】 系列专栏:【❤️周末闲谈】 系列目录 ✨第一周 二进制VS三进制 ✨第二周 文心一…...

sklearn垃圾邮件分类
在Python中,可以使用机器学习算法来进行垃圾邮件分类。下面是一个简单的示例,使用朴素贝叶斯算法进行垃圾邮件分类: import pandas as pd from sklearn.feature_extraction.text import CountVectorizer from sklearn.model_selection impor…...

UI美工设计岗位的工作职责
UI美工设计岗位的工作职责1 职责: 1、负责软件界面的美术设计、创意工作和制作工作; 2、根据各种相关软件的用户群,提出构思新颖、有高度吸引力的创意设计; 3、对页面进行优化,使用户操作更趋于人性化; 4、维护现有的应用产品; 5、收集和…...
的正确打开方式)
ES6链判断运算符(?.)的正确打开方式
在实际应用中,如果读取对象内部 的某个属性,往往需要判断一下,属性的上层对象是否存在。比如,读取message.body.user.firstName这个属性,安全的写法是写成下下面这样: // 错误的写法 const firstName mes…...

删除块参照 删除块定义
删除块参照 void CDwgDatabaseUtil::DeleteBlockReference(CString strBlockName) {// 锁定文档acDocManager->lockDocument(acDocManager->curDocument());AcDbObjectId objRecId;if (...
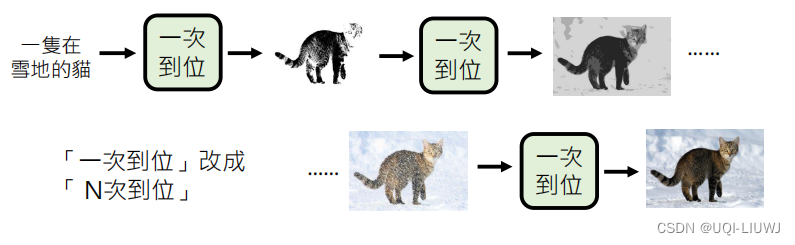
机器学习笔记:李宏毅ChatGPT:生成式学习的两种策略
1 策略1 “各个击破”——autoregressive model “各个击破”——一个一个生成出来 2 策略2 : “一次到位”——non-autoregressve model 一步到位,全部生成出来 2.1 non-autoregressive model 如何确定长度? 两种策略 策略1:始…...
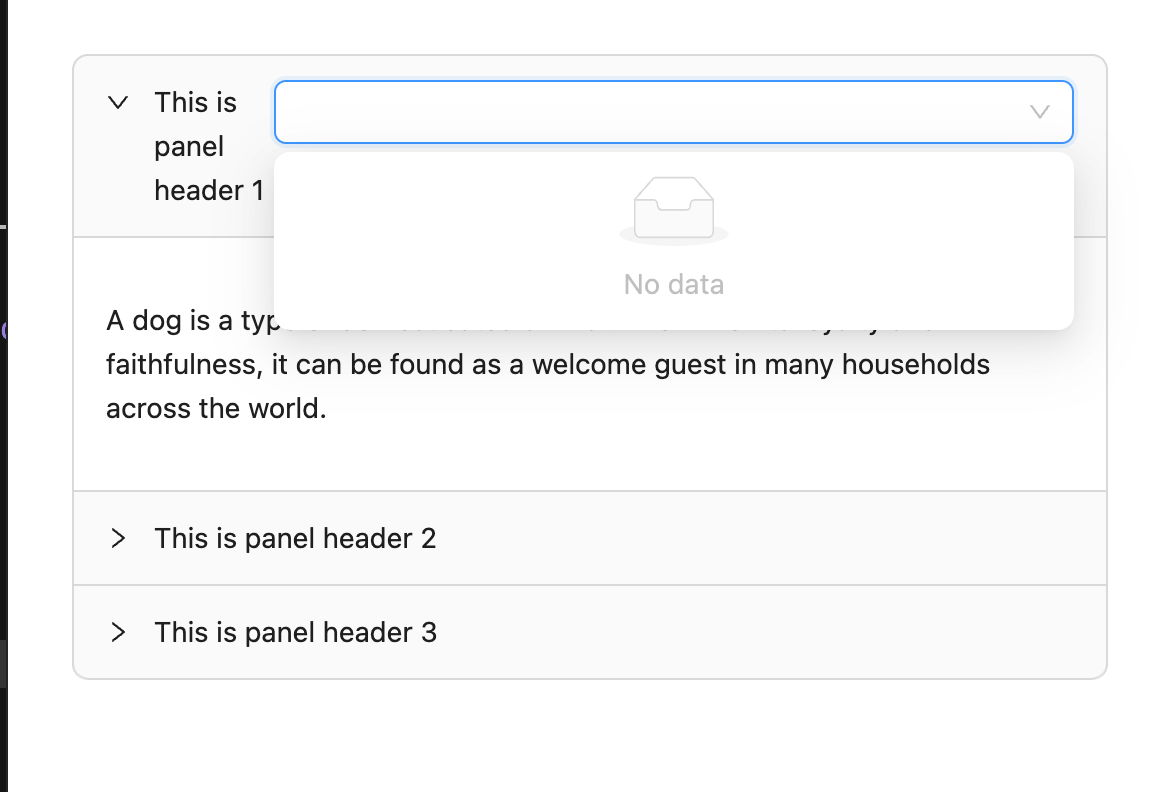
React 组件防止冒泡方法
背景 在使用 antd 组件库开发时,发现点击一个子组件,却触发了父组件的点击事件,比如,我在一个折叠面板里面放入一个下拉框或者对下拉框列表渲染做定制,每个下拉框候选项都有一个子组件… 解决 其实这就是 Javascri…...
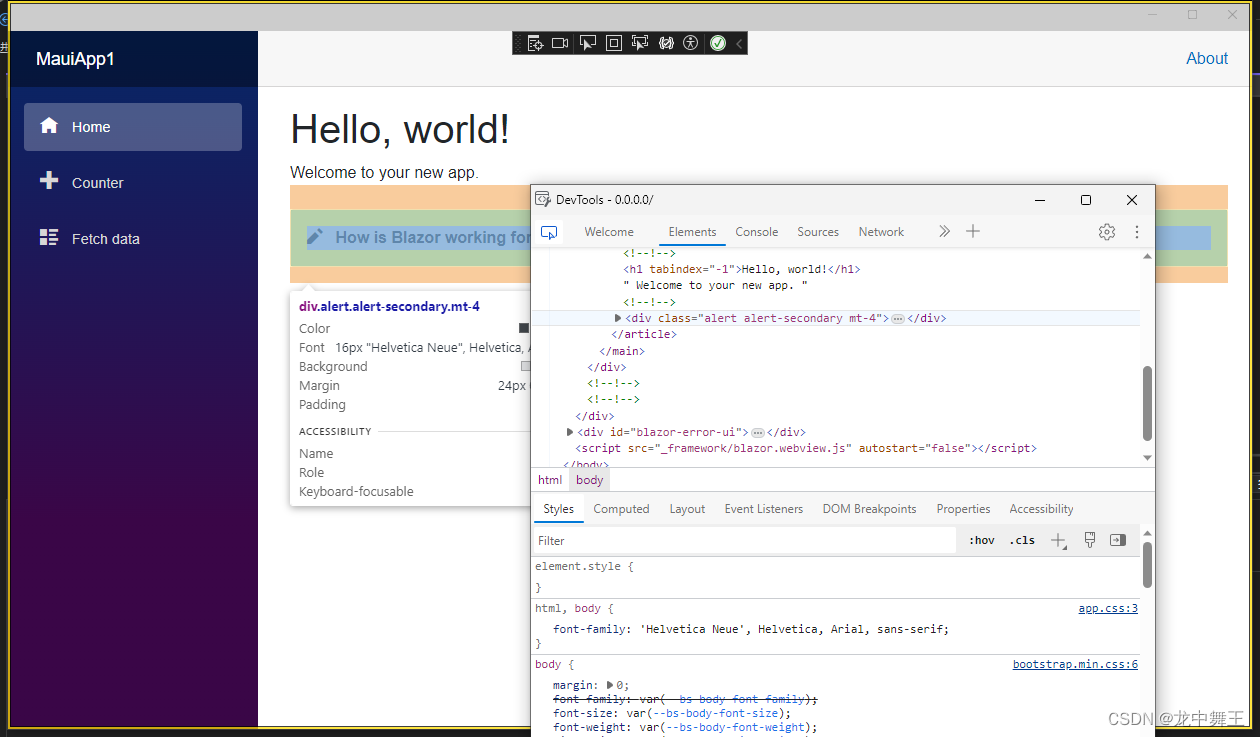
MAUI+Blazor 如何开启浏览器调试工具
文章目录 前言如何开启调试模式输入快捷键打开浏览器有什么意义? 前言 MAUIBlazor其实就是浏览器套壳,我觉得很有意义,因为现在性能已经不是主要的限制了,很多时候讲究的快速开发。而且MAUIBlazor跨平台的未来感觉实在是太香了。…...
【Spring MVC】Spring MVC基于注解的程序开发
目录 一、什么是Spring MVC 二、Spring MVC项目的创建和使用 1、实现客户端和服务器端之间的连接 1.1、RequsestMapping注解 1.2、RequestMapper的简单使用 1.3、使用GetMapping和POSTMapping注解来实现HTTP连接 三、获取参数 1、实现获取单个参数 2、实现获取对象 3…...

前端探索之旅
目录 简介:内容大纲:第一章 前端开发简介1.1 前端开发的定义和作用1.2 前端开发的职责1.3 前端开发的技能要求1.4 前端开发的发展前景总结: 第二章 HTML基础2.1 HTML基本结构2.2 常见HTML标签和元素 第三章 CSS基础3.1 CSS基本语法3.2 常见CSS选择器3.3 常见CSS属性…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

论文阅读:LLM4Drive: A Survey of Large Language Models for Autonomous Driving
地址:LLM4Drive: A Survey of Large Language Models for Autonomous Driving 摘要翻译 自动驾驶技术作为推动交通和城市出行变革的催化剂,正从基于规则的系统向数据驱动策略转变。传统的模块化系统受限于级联模块间的累积误差和缺乏灵活性的预设规则。…...

渗透实战PortSwigger靶场:lab13存储型DOM XSS详解
进来是需要留言的,先用做简单的 html 标签测试 发现面的</h1>不见了 数据包中找到了一个loadCommentsWithVulnerableEscapeHtml.js 他是把用户输入的<>进行 html 编码,输入的<>当成字符串处理回显到页面中,看来只是把用户输…...

Visual Studio Code 扩展
Visual Studio Code 扩展 change-case 大小写转换EmmyLua for VSCode 调试插件Bookmarks 书签 change-case 大小写转换 https://marketplace.visualstudio.com/items?itemNamewmaurer.change-case 选中单词后,命令 changeCase.commands 可预览转换效果 EmmyLua…...

React从基础入门到高级实战:React 实战项目 - 项目五:微前端与模块化架构
React 实战项目:微前端与模块化架构 欢迎来到 React 开发教程专栏 的第 30 篇!在前 29 篇文章中,我们从 React 的基础概念逐步深入到高级技巧,涵盖了组件设计、状态管理、路由配置、性能优化和企业级应用等核心内容。这一次&…...
